Vous êtes ici

Transformations - Isométries du plan - T S1

I Définitions

On appelle transformation du plan toute application bijective du plan dans lui-même.

$f$ est une transformation du plan

$\mathcal{P}$ si

$\forall\;M\in\mathcal{P}$ ,

$\exists$ un unique point

$N$ tel que

$f(N)=N.$

Exemple :

translation , homothéties, symétries, rotation, affinités

La projection n'est pas une transformation

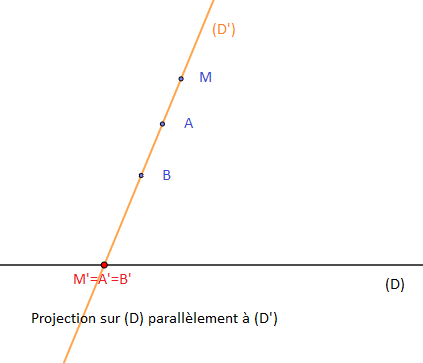
II Exemples

II.1 Translation

II.1.1 Définitions

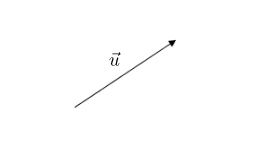
Soit

$\vec{u}$ un vecteur non nul.

On appelle translation de vecteur

$\vec{u}$ la transformation du plan notée

$t_{\vec{u}}$ qui associe, à tout point

$M$ de

$\mathcal{P}$ , le point

$M'$ tel que

$\overrightarrow{MM'}=\vec{u}$ .

II.1.2 Ensembles invariants

$\centerdot\ \$ Un point

$M$ est invariant par une transformation

$f$ si

$\ f(M)=M$ . L'ensemble des points invariants est noté InV

$f$ .

$\centerdot\ \$ Un ensemble

$E$ est dit globalement invariant par une transformation

$f$ si

$\ f(E)=E$ .

$\centerdot\ \$ InV

$t_{\vec{u}}=\emptyset$

$\centerdot\ \$ Toute droite de direction

$\vec{u}$ est globalement invariant par

$t_{\vec{u}}$

II.1.3 Propriétés

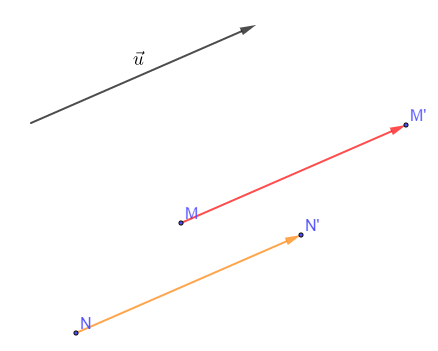
$\centerdot\ \$ Propriété caractéristique : soient

$M\$ et

$\ N$ deux points du plan d'images respectives

$M'\$ et

$\ N'$ par

$t_{\vec{u}}$ .

Nous avons

$t_{\vec{u}}(M)=M'$ si, et seulement si,

$\overrightarrow{MM'}=\vec{u}$

De même

$t_{\vec{u}}(N)=N'$ si, et seulement si,

$\overrightarrow{NN'}=\vec{u}$

Ce qui entraine :

$\overrightarrow{MM'}=\overrightarrow{NN'}$

D'où,

$(MM'N'N)$ est un parallélogramme

$\centerdot\ \$ Une transformation

$f$ conserve le barycentre si pour

$G$ barycentre de

$(A_{i},\ \alpha_{i})_{1\leq i\leq n}$ alors

$f(G)$ est barycentre de

$(f(A_{i}),\ \alpha_{i})_{1\leq i\leq n}$

$G$ est barycentre de

$(A,\ \alpha)$ ,

$\ (B,\ \beta)$ ,

$\ (C,\ \gamma)$ avec

$\alpha + \beta + \gamma \neq 0$ alors,

$\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}=\vec{0}$

Ainsi, si

$t_{\vec{u}}(G)=G'$ ,

$\ t_{\vec{u}}(A)=A'$ ,

$\ t_{\vec{u}}(B)=B'$ et

$t_{\vec{u}}(C)=C'$ alors

$\overrightarrow{G'A'}=\overrightarrow{GA}$ ,

$\$

$\overrightarrow{G'B'}=\overrightarrow{GB}$ et

$\overrightarrow{G'C'}=\overrightarrow{GC}$

Et par suite,

$\alpha\overrightarrow{G'A'}+\beta\overrightarrow{G'B'}+\gamma\overrightarrow{G'C'}=\vec{0}$ avec

$\alpha + \beta + \gamma \neq 0$

Donc,

$G'$ est barycentre de

$(A',\ \alpha)$ ,

$\ (B',\ \beta)$ ,

$\ (C',\ \gamma)$

La translation conserve le barycentre. Elle conserve aussi le produit scalaire.

$\centerdot\ \$

$t_{\vec{u}}(M)=M'$ et

$t_{\vec{u}}(N)=N'$ alors

$\overrightarrow{M'N'}=\overrightarrow{MN}$

Ce qui donne,

$||\overrightarrow{M'N'}||=||\overrightarrow{MN}||$

Ainsi, la translation du vecteur

$\vec{u}$ conserve la distance.

Une transformation du plan qui conserve la distance est appelée une isométrie. Donc la translation est une isométrie.

$\centerdot\ \$ Soient trois points

$A$ ,

$\ B$ et

$C$ d'images respectives

$A'$ ,

$\ B'$ et

$C'$ par

$t_{\vec{u}}$ ;

$\overrightarrow{A'B'}=\overrightarrow{AB}$ et

$\overrightarrow{A'C'}=\overrightarrow{AC}$ alors on a :

$\left(\overrightarrow{AB},\ \overrightarrow{AC}\right)=\left(\overrightarrow{A'B'},\ \overrightarrow{A'C'}\right)$

Donc, la translation de vecteur

$\vec{u}$ conserve les angles orientés.

Une transformation du plan qui conserve les distances et la angles orientés est appelée un déplacement.

Donc une translation est un déplacement.

$\centerdot\ \$

$t_{\vec{u}}(M)=M'$ et

$t_{\vec{u}}(N)=N'$

$\Longrightarrow \: \overrightarrow{M'N'}=\overrightarrow{MN}$

Donc,

$\overrightarrow{M'N'}$ et

$\overrightarrow{MN}$ sont colinéaires.

D'où, l'image d'une droite est une droite qui lui est parallèle.

En conclusion la translation conserve :

$\centerdot\ \$ l'alignement

$\centerdot\ \$ le parallélisme

$\centerdot\ \$ l'orthogonalité

$\centerdot\ \$ le barycentre

$\centerdot\ \$ les distances

$\centerdot\ \$ les angles orientés

Aussi, l'image d'une figure quelconque est une figure de même nature.

II.1.4 Expression complexe et analytique

Soient

$\vec{u}\begin{pmatrix} a\\b\end{pmatrix}$ ;

$\ z_{\vec{u}}=a+ib$ .

$\ M\begin{pmatrix} x\\y \end{pmatrix}$ et

$M'\begin{pmatrix} x'\\y'\end{pmatrix}$ ;

$\ t_{\vec{u}}(M)=M'$ .

$M$ d'affixe

$z$ noté

$M(z)\;;\ z=x+\mathrm{i}y$ et

$M'$ d'affixe

$z'$ noté

$M'(z')\;;\ z'=x'+\mathrm{i}y'$

On a :

$\begin{eqnarray} \overrightarrow{MM'}=\vec{u}&\Leftrightarrow&z_{\overrightarrow{MM'}}=z_{\vec{u}}\nonumber \\ \\&\Leftrightarrow&z-z'=z_{\vec{u}}\nonumber \\ \\&\Leftrightarrow&z'=z+z_{\vec{u}}\nonumber \end{eqnarray}$

$z'=z+\alpha$ est l'expression complexe d'une translation de vecteur

$\vec{u}(\alpha)$ avec

$\alpha=z_{\vec{u}}$

Nous avons :

$\begin{eqnarray} z'=z+z_{\vec{u}}\ \Rightarrow\ x'+\mathrm{i}y'&=&x+\mathrm{i}y+a+ib\nonumber \\ \\&=&x+a+\mathrm{i}(y+b)\nonumber \end{eqnarray}$

Ainsi,

$\left\lbrace\begin{array}{lcl} x'&=&x+a \\ y'&=&y+b\end{array}\right.$ est l'expression analytique d'une translation.

II.1.5 Composée et réciproque

Soit

$t$ une translation,

$M$ un point du plan d'image

$M'$ par

$t$ .

On a :

$t_{\vec{0}}=Id$ .

En effet,

$t_{\vec{0}}(M)=M'$ si et seulement si

$\overrightarrow{MM'}=\vec{0}$ . Donc

$M=M'$

Soient deux vecteurs

$\vec{u}$ et

$\vec{v}$ non nuls alors

$t_{\vec{u}}\circ t_{\vec{v}}=t_{\vec{u}+\vec{v}}$

Et donc,

$t_{\vec{u}}\circ t_{\vec{v}}(M)=t_{\vec{u}}[t_{\vec{v}}(M)]=t_{\vec{u}}(M_{1})=M'$

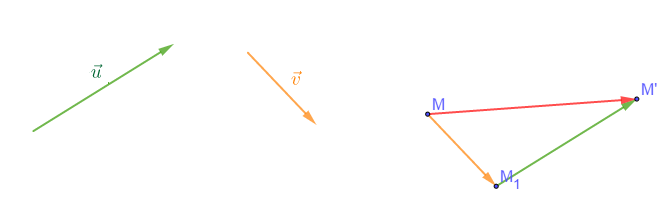
En effet,

$t_{\vec{v}}(M)=M_{1}$ ,

$\ t_{\vec{u}}(M_{1})=M'$

$\overrightarrow{MM'}=\overrightarrow{MM}_{1}+\overrightarrow{M_{1}M'}=\vec{u}+\vec{v}$

Donc,

$t_{\vec{u}}\circ t_{\vec{v}}=t_{\vec{u}+\vec{v}}$

Soient

$\vec{u}(\alpha)$ et

$\vec{v}(\beta)$ deux vecteurs d'affixes respectifs

$\alpha$ et

$\beta$

On a :

$t_{\vec{u}}$ :

$z'=z+\alpha$ et

$t_{\vec{v}}$ :

$z'=z+\beta$

Alors, la composée

$t_{\vec{u}}\circ t_{\vec{v}}$ sera définie par :

$z'=z+\beta+\alpha$ avec

$\beta+\alpha$ affixe de

$\vec{u}+\vec{v}$

$t_{\vec{u}}$ une translation de vecteur

$\vec{u}$ alors on a :

$\begin{eqnarray} t_{\vec{u}}(M)=M'&\Leftrightarrow&\overrightarrow{MM'}=\vec{u}\nonumber \\ \\&\Leftrightarrow&\overrightarrow{M'M}=-\vec{u}\nonumber \\ \\&\Leftrightarrow&M=t_{-\vec{u}}(M')\nonumber \end{eqnarray}$

Donc,

$\left(t_{\vec{u}}\right)^{-1}=t_{-\vec{u}}$

La réciproque de la translation de vecteur

$\vec{u}$ est la translation de vecteur

$-\vec{u}.$

Exercice d'application

Soit

$f$ l'application qui, à tout

$M\begin{pmatrix} x \\ y\end{pmatrix}$ , associe le point

$M'\begin{pmatrix} x' \\ y'\end{pmatrix}$ tels que

$\left\lbrace\begin{array}{rcl} x'&=&x-2 \\ y'&=&y+1\end{array}\right.$

1) Déterminer InV

$f$

2) Montrer que

$f$ est une translation de vecteur

$\vec{u}$ dont on donnera les éléments caractéristiques.

3) Déterminer les images de

$A\begin{pmatrix} 1 \\ 2\end{pmatrix}\;,\ C\left(B\begin{pmatrix} 0 \\ 3\end{pmatrix}\;;\ 5\right)\$ et

$\ D\ :\ y-2x+1=0$

4) Donner l'expression complexe

Résolution

$\begin{eqnarray} M\in\text{InV}f&\Leftrightarrow&f(M)=M\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&x \\ y'&=&y\end{array}\right.\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&x-2 \\ y&=&y+1\end{array}\right.\quad\text{impossible}\nonumber \end{eqnarray}$

Donc, InV

$f=\emptyset$

2) Soit

$M'\begin{pmatrix} x' \\ y'\end{pmatrix}$ image de

$M\begin{pmatrix} x \\ y\end{pmatrix}$ par

$f\;;\ \overrightarrow{MM}'\begin{pmatrix} x'-x \\ y'-y\end{pmatrix}$ , alors

$\begin{eqnarray} f(M)=M'&\Rightarrow&\left\lbrace\begin{array}{rcl} x'&=&x-2 \\ y'&=&y+1\end{array}\right.\nonumber \\ \\&\Rightarrow&\left\lbrace\begin{array}{rcl} x'-x&=&-2 \\ y'-y&=&1\end{array}\right.\nonumber\\ \\ &\Rightarrow&\overrightarrow{MM}'\begin{pmatrix} x'-x \\ y'-y\end{pmatrix}=\vec{\omega}\begin{pmatrix} -2 \\ 1\end{pmatrix}\nonumber \end{eqnarray}$

Soit

$\vec{u}=\vec{\omega}$ , alors

$f$ est une translation de vecteur

$\vec{u}=-2\vec{i}+\vec{j}$

$\begin{eqnarray} \text{Soit }\ A'=t_{\vec{u}}(A)\;,\text{ alors }\left\lbrace\begin{array}{rcl} x_{A'}&=&x_{A}-2 \\ y_{A'}&=&y_{A}+1\end{array}\right.&\Rightarrow&\left\lbrace\begin{array}{rcl} x_{A'}&=&1-2 \\ y_{A'}&=&2+1\end{array}\right.\nonumber \\ \\&\Rightarrow&A'\begin{pmatrix} -1 \\ 3\end{pmatrix}\nonumber \end{eqnarray}$

On a :

$t_{\vec{u}}(C)=C'(B'\;;\ 5)$ .

Soit

$B'=t_{\vec{u}}(B)$ , alors

$\left\lbrace\begin{array}{rcl} x_{B'}&=&x_{B}-2 \\ y_{B'}&=&y_{B}+1\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{rcl} x_{B'}&=&-2 \\ y_{B'}&=&4\end{array}\right.$

Donc,

$C'\left(B'\begin{pmatrix} -2 \\ 4\end{pmatrix}\;;\ 5\right)$

Soit

$D'=t_{\vec{u}}(D)$ alors,

$D'//D$ et donc,

$D'\ :\ y-2x+c=0$

Déterminons la constante

$c$

Soit

$E\begin{pmatrix} 0 \\ -1\end{pmatrix}\in D$ alors,

$t_{\vec{u}}(E)=E'\begin{pmatrix} x' \\ y'\end{pmatrix}\in D'.$

On a :

$\left\lbrace\begin{array}{rcl} x_{E'}&=&x_{E}-2 \\ y_{E'}&=&y_{E}+1\end{array}\right.\ \Rightarrow\ E'\begin{pmatrix} -2 \\ 0\end{pmatrix}$

$E'\in D'$ , alors

$4+c=0\ \Rightarrow\ c=-4$ . Donc

$D'\ :\ y-2x-4=0$

4) Soit

$z=x+\mathrm{i}y$ l'affixe de

$M$ et

$z'=x'+\mathrm{i}y'$ celui de

$M'$ , alors

$\begin{eqnarray} z'&=&x'+\mathrm{i}y'\nonumber \\ \\&=&x-2+\mathrm{i}(y+1)\nonumber \\ \\&=&x+\mathrm{i}y-2+\mathrm{i}\nonumber\\ \\ &=&z-2+\mathrm{i}\nonumber \end{eqnarray}$

Donc,

$z'=z-2+\mathrm{i}$ est l'expression complexe de cette transformation.

II.2 Homothéties

II.2.1 Définitions

Soit

$\Omega$ un point du plan ,

$k \in\mathbb{R}^{*}\setminus \{1\}$ . On appelle homothétie de centre

$\Omega$ et de rapport

$k$ la transformation du plan notée

$h_{(\Omega,\ k)}$ qui laisse

$\Omega$ invariant et qui associe à tout point

$M$ différent de

$\Omega$ le point

$M'$ tel que

$\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$

$h_{(\Omega,\ k)}(M)=M' \: \Leftrightarrow \: \overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$

II.2.2 Ensembles invariants

$\centerdot\ \$ InV

$h_{(\Omega,\ k)}=\{\Omega\}$ .

$\ \Omega$ est ici le seul point invariant.

Soit

$M \in$ InV

$h_{(\Omega,\ k)}$

Nous avons :

$h_{(\Omega,\ k)}(M)=M$ si, et seulement si,

$\overrightarrow{\Omega M}=k\overrightarrow{\Omega M}$

Ce qui donne :

$\overrightarrow{\Omega M}(1-k)=\vec{0}$ or

$1-k\neq 0$

Et donc,

$\overrightarrow{\Omega M}=\vec{0}$ . D'où,

$\Omega=M$

$\centerdot\ \$ Toute droite passant par

$\Omega$ est globalement invariant par

$h_{(\Omega,\ k)}$ car

$\Omega$ ,

$\ M$ et

$M'$ alignés.

II.2.3 Propriétés

$\centerdot\ \$

$h_{(\Omega,\ k)}(M)=M' \: \Longrightarrow \: \Omega, \; M, \; M'$ alignés.

$\centerdot\ \$

$h_{(\Omega,\ k)}(M)=M'$ alors

$\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$

$h_{(\Omega,\ k)}(N)=N'$ alors,

$\overrightarrow{\Omega N'}=k\overrightarrow{\Omega N}$

Ce qui entraine

$\overrightarrow{M'N'}=k\overrightarrow{MN}$

$\centerdot\ \ G$ barycentre de

$(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$ , alors

$\alpha_{1}\overrightarrow{GA}_{1}+\alpha_{2}\overrightarrow{GA}_{2}+\ldots+\alpha_{n}\overrightarrow{GA}_{n}=\vec{0}.$

$\begin{eqnarray} h_{(\Omega, k)}(G)=G'\text{ et }h_{(\Omega, k)}(A_{i})=A_{i}'&\Rightarrow&\overrightarrow{G'A'_{i}}=k\overrightarrow{GA_{i}}\nonumber\\ \\ &\Rightarrow&k\alpha_{1}\overrightarrow{GA}_{1}+k\alpha_{2}\overrightarrow{GA}_{2}+\ldots+k\alpha_{n}\overrightarrow{GA}_{n}=\vec{0}\nonumber\\ \\ &\Rightarrow&\alpha_{1}\overrightarrow{G'A'}_{1}+\alpha_{2}\overrightarrow{G'A'}_{2}+\ldots+\alpha_{n}\overrightarrow{G'A'}_{n}=\vec{0}\nonumber \end{eqnarray}$

Ce qui montre que

$G'$ est aussi barycentre de

$(A_{i},\ \alpha_{i})_{1\leq i\leq n}$

Donc, il y a conservation du barycentre d'où, l'image d'une droite est une droite qui lui est parallèle car

$\overrightarrow{M'N'}$ colinéaire à

$\overrightarrow{MN}$

$\centerdot\ \$

$\overrightarrow{M'N'}=k\overrightarrow{MN} \: \Rightarrow \: M'N'=|k|.MN$

$|k|\neq 1$ , la distance n'est pas conservée. L'homothétie de rapport

$|k|\neq 1$ multiplie :

$\centerdot\ \$ les distances par

$|k|$

$\centerdot\ \$ les aires par

$k^{2}$

$\centerdot\ \$ les volumes par

$k^{3}$

$\centerdot\ \$ soient

$h_{(\Omega,\ k)}(A)=A'$ ,

$h_{(\Omega,\ k)}(B)=B'$ et

$h_{(\Omega,\ k)}(C)=C'$ alors on a :

$\begin{eqnarray} \overrightarrow{A'B'}=k\overrightarrow{AB}\text{ et }\overrightarrow{A'C'}=k\overrightarrow{AC}\ \Rightarrow\ \left(\overrightarrow{A'B'}\;,\ \overrightarrow{A'C'}\right)&=&\left(k\overrightarrow{AB}\;,\ k\overrightarrow{AC}\right)\nonumber \\ &=&\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)\nonumber \end{eqnarray}$

Donc, les angles orientés sont conservés.

L'homothétie conserve :

$\centerdot\ \$ le barycentre

$\centerdot\ \$ les angles orientés

$\centerdot\ \$ la perpendiculaire

$\centerdot\ \$ le parallélisme

L'image d'une figure quelconque est une figure de même nature.

II.2.4 Expression analytique et complexe

Soient

$\Omega\begin{pmatrix} a\\ b \end{pmatrix}$ d'affixe

$z_{\Omega}=a+\mathrm{i}b=\alpha\$ ,

$\ M\begin{pmatrix} x\\ y \end{pmatrix}$ d'affixe

$z_{M}=z=x+\mathrm{i}y$ et

$M'\begin{pmatrix} x'\\ y'\end{pmatrix}$ d'affixe

$z_{M'}=z'=x'+\mathrm{i}y'.$

On a :

$\begin{eqnarray} h_{(\Omega\;,\ k)}(M)=M'&\Leftrightarrow&\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}\nonumber\\ \\ &\Leftrightarrow&z'-z_{\Omega}=k(z-z_{\Omega})\nonumber\\ \\ &\Leftrightarrow&z'=kz+(1-k)z_{\Omega}\nonumber \end{eqnarray}$

Ainsi,

$z'=kz+\beta$ est l'expression complexe d'une homothétie.

Autrement,

$\begin{eqnarray} z'-z_{\Omega}=k(z-z_{\Omega})&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'-a&=&k(x-a)\\ y'-b&=&k(y-b)\end{array}\right.\nonumber\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&kx+\alpha_{1}\\ y'&=&ky+\beta_{1}\end{array}\right.\nonumber \end{eqnarray}$ Ce dernier système détermine l'expression analytique d'une homothétie.

Exercice d'application

Soit

$f$ l'application définie par

$\left\lbrace\begin{array}{rcl} x'&=&x-2 \\ y'&=&y+1\end{array}\right.$ qui, à tout

$M\begin{pmatrix} x \\ y\end{pmatrix}$ , associe le point

$M'\begin{pmatrix} x' \\ y'\end{pmatrix}$

1) Déterminer InV

$f$

2) Montrer que

$f$ est une homothétie dont on donnera les éléments caractéristiques.

3) Déterminer l'expression complexe

4) Déterminer les images de

$O\begin{pmatrix} 0 \\ 0\end{pmatrix}\;,\ C\left(I\begin{pmatrix} 1 \\ 3\end{pmatrix}\;;\ 5\right)\$ et

$\ D\ :\ 2x-y+3=0$

Résolution

$\begin{eqnarray} M\in\text{InV}f&\Leftrightarrow&f(M)=M\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&x \\ y'&=&y\end{array}\right.\nonumber\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&2x-1 \\ y&=&2y+3\end{array}\right.\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&1 \\ y&=&-3\end{array}\right.\nonumber \end{eqnarray}$

Donc InV

$f=\Omega\begin{pmatrix} 1 \\ -3\end{pmatrix}$

2) Soit

$M'\begin{pmatrix} x' \\ y'\end{pmatrix}$ image de

$M\begin{pmatrix} x \\ y\end{pmatrix}$ par

$f$ , alors

$\begin{eqnarray} \overrightarrow{\Omega M}'\begin{pmatrix} x'-1 \\ y'+3\end{pmatrix}&\Leftrightarrow&\begin{pmatrix} 2x-1-1 \\ 2y+3+3\end{pmatrix}\nonumber\\ \\ &\Leftrightarrow&\begin{pmatrix} 2x-2 \\ 2y+6\end{pmatrix}\nonumber\\ \\ &\Leftrightarrow&\begin{pmatrix} 2(x-1) \\ 2(y+3)\end{pmatrix}\quad\text{or }\ \overrightarrow{\Omega M}\begin{pmatrix} x-1 \\ y+3\end{pmatrix}\nonumber \\ \Rightarrow\ \overrightarrow{\Omega M}'&=&2\overrightarrow{\Omega M}\nonumber \end{eqnarray}$

Soit

$\overrightarrow{\Omega M}'=2\overrightarrow{\Omega M}$ , donc

$f$ est une homothétie de centre

$\Omega$ et de rapport 2. Ainsi,

$M'=h_{(\Omega\;,\ 2)}$

3) Soit

$z=x+\mathrm{i}y$ l'affixe de

$M$ et

$z'=x'+\mathrm{i}y'$ celui de

$M'$ , alors

$\begin{eqnarray} z'&=&x'+\mathrm{i}y'\nonumber \\ \\&=&2x-1+\mathrm{i}(2y+3)\nonumber\\ \\ &=&2x+2\mathrm{i}y-1+3\mathrm{i}\nonumber\\ \\ &=&2(x+\mathrm{i}y)-1+3\mathrm{i}\nonumber\\ \\ &=&2z-1+3\mathrm{i}\nonumber \end{eqnarray}$

Donc,

$z'=2z-1+3\mathrm{i}$ est l'expression complexe de cette transformation.

$\begin{eqnarray} \text{Soit }\ O'=h_{(\Omega\;,\ 2)}(O)\;,\text{ alors }z_{O'}&=&2z_{O}-1+3\mathrm{i}\nonumber \\ \\&=&-1+3\mathrm{i}\nonumber \end{eqnarray}$

Donc,

$O'\begin{pmatrix} -1 \\ 3\end{pmatrix}$

On a :

$h_{(\Omega\;,\ 2)}(C)=C'(I'\;;\ 10)$ .

$\begin{eqnarray} \text{Soit }\ I'=h_{(\Omega\;,\ 2)}(I)\;,\text{ alors }z_{I'}&=&2z_{I}-1+3\mathrm{i}\nonumber\\ \\ &=&2(1+3\mathrm{i})-1+3\mathrm{i}\nonumber\\ \\ &=&2+6\mathrm{i}-1+3\mathrm{i}\nonumber\\ \\ &=&1+9\mathrm{i}\nonumber \end{eqnarray}$

Donc,

$I'\begin{pmatrix} 1 \\ 9\end{pmatrix}$

Soit

$D'=h_{(\Omega\;,\ 2)}(D)$ , alors

$D'//D$ et donc

$D'\ :\ 2x-y+c=0.$

Déterminons la constante

$c$

Soit

$B\begin{pmatrix} 0 \\ 3\end{pmatrix}\in D$ , alors

$\begin{eqnarray} B'=h_{(\Omega\;,\ 2)}(B)\ \Rightarrow\ z_{B'}&=&2z_{B}-1+3\mathrm{i}\nonumber\\ \\ &=&2(0+3\mathrm{i})-1+3\mathrm{i}\nonumber\\ \\ &=&6\mathrm{i}-1+3\mathrm{i}\nonumber\\ \\ &=&-1+9\mathrm{i}\nonumber \end{eqnarray}$

Donc,

$B'\begin{pmatrix} -1 \\ 9\end{pmatrix}\in D'$ , alors

$-2-9+c=0\ \Rightarrow\ c=11$ . Donc

$D'\ :\ 2x-y+11=0.$

II.2.5 Composée et réciproque

$\centerdot\ \$

$\begin{eqnarray} h_{(\Omega\;,\ k)}(M)=M'&\Rightarrow&\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}\nonumber\\ \\ &\Rightarrow&\overrightarrow{\Omega M}=\dfrac{1}{k}\overrightarrow{\Omega M'}\nonumber\\ \\ &\Rightarrow&M=h_{(\Omega\;,\ \frac{1}{k})}(M')\nonumber \end{eqnarray}$

Donc,

$\left(h_{(\Omega,\ k)}\right)^{-1}=h_{(\Omega,\ \frac{1}{k})}$

La réciproque d'une homothétie de centre

$\Omega$ et de rapport

$k$ est l'homothétie de centre

$\Omega$ et de rapport

$\dfrac{1}{k}$

$\centerdot\ \$ Soient

$h_{1}$ et

$h_{2}$ deux homothéties de même centre

$\Omega$ telles que

$h_{1}=h_{(\Omega,\ k)}$ et

$h_{2}=h_{(\Omega,\ k')}$

$\centerdot\ \$ si

$kk'=1$ alors

$h_{1}\circ h_{2}=Id$ .

$\centerdot\ \$ si

$kk'\neq 1$ alors

$h_{1}\circ h_{2}=h_{(\Omega,\ kk')}$

$\centerdot\ \$

$h_{1}$ et

$h_{2}$ sont de centres différents ;

$h_{1}=h_{(\Omega_{1},\ k_{1})}$ et

$h_{2}=h_{(\Omega_{2},\ k_{2})}$ .

On a :

$h_{1}$ :

$z'=k_{1}z+\alpha$ ,

$\ h_{2}$ :

$z'=k_{2}z+\beta$

Donc,

$h_{1}\circ h_{2}$ :

$z'=k_{2}(k_{1}z+\alpha)+\beta=k_{2}k_{1}z+\alpha+\beta$

$\Rightarrow \: h_{1}\circ h_{2}\: : k_{2}k_{1}z+a$ avec

$a=\alpha+\beta$

$\centerdot\ \$ si

$kk'=1$ alors

$h_{1}\circ h_{2}$ est une translation.

$\centerdot\ \$ si

$kk'\neq 1$ alors

$h_{1}\circ h_{2}$ est une homothétie de rapport

$k_{1}k_{2}$ et de centre le point invariant.

$\centerdot\ \$ Remarques :

$h_{(\Omega,\ -1)}=S_{\Omega}$ , car

$\overrightarrow{\Omega M'}=-\overrightarrow{\Omega M}$

$\Longrightarrow \Omega$ est milieu de

$[AB]$

II.3 Réflexion

II.3.1 Définition

Soit

$\Delta$ une droite. On appelle réflexion d'axe

$\Delta$ la transformation du plan qui laisse tout point de

$\Delta$ invariant et qui associe à

$M \notin\Delta$ le point

$M'$ tel que

$\Delta$ soit la médiatrice de

$[AB].$

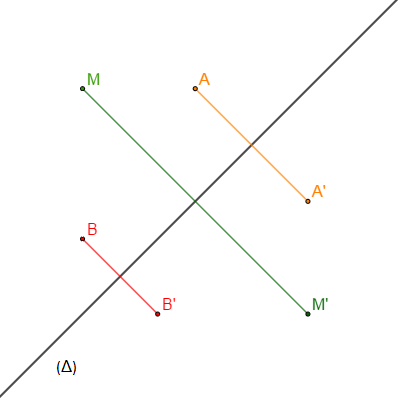
II.3.2 Propriétés

$\centerdot\ \$ InV

$S_{\Delta}=(\Delta)$

$\centerdot\ \$ Toute perpendiculaire à

$\Delta$ est globalement invariant par

$S_{\Delta}$

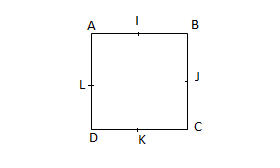
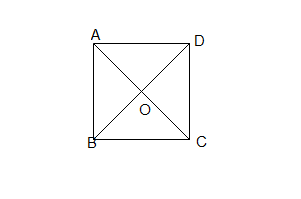
$\centerdot\ \$

$ABCD$ un carré ;

$S_{BD}$ ,

$\ S_{AC}$ ,

$\ S_{IK}$ et

$S_{JL}$ laissent invariant le carré.

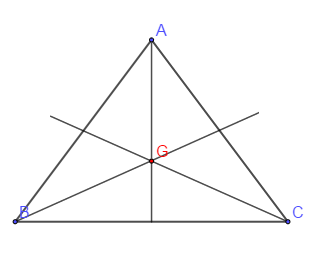
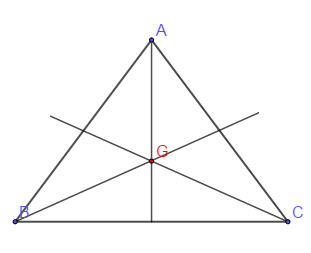
$\centerdot\ \$

$ABC$ un triangle équilatérale ;

$S_{AG}$ ,

$\ S_{BG}$ et

$S_{CG}$ laissent invariant le triangle ;

$G$ isobarycentre de

$ABC.$

$\centerdot\ \$ La symétrie axiale conserve :

$\centerdot\ \$ les angles consécutifs mais change le signe des angles orientés.

$\centerdot\ \$ les distances

$\centerdot\ \$ le parallélisme

La symétrie axiale est un antidéplacement ou isométrie négative. L'image d'une figure quelconque est une figure de même nature et de même dimension.

II.3.3 Expression analytique et complexe

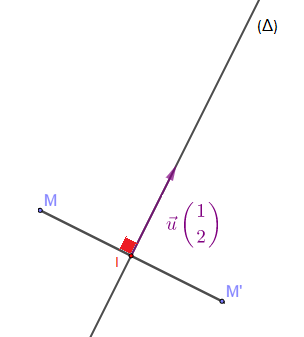
Soit

$(\Delta)$ la droite d'équation :

$2x-y+3=0$ . On se donne

$M\begin{pmatrix} x\\y\end{pmatrix}$ un point du plan d'image

$M'\begin{pmatrix} x'\\y'\end{pmatrix}$ par la réflexion d'axe

$(\Delta)$ . Soient

$\vec{u}\begin{pmatrix} 1\\2\end{pmatrix}$ vecteur directeur de

$(\Delta)$ et

$I\begin{pmatrix}\dfrac{x+x'}{2}\\ \\ \dfrac{y+y'}{2}\end{pmatrix}$ milieu de

$[MM']$ , donc

$I\in\Delta$ . On a :

$\begin{array}{rcl} S_{\Delta}(M)=M'&\Leftrightarrow&\overrightarrow{MM'}\cdot\vec{u}=\vec{0}\ \text{ et }\ I\in\Delta\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 1(x'-x)+2(y'-y)&=&0 \\ \\ 2\left(\dfrac{x+x'}{2}\right)-\left(\dfrac{y+y'}{2}\right)+3&=&0\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'+2y'-x-2y&=&0 \\ 2x'-y'+2x-y+6&=&0\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&\dfrac{1}{5}(-3x+4y-12) \\ \\ y'&=&\dfrac{1}{5}(4x+3y+6) \end{array}\right.\end{array}$

Ce dernier système définit une expression analytique de la réflexion

$S_{\Delta}$ .

En écriture complexe on a :

$M\begin{pmatrix} x\\ y \end{pmatrix}$ d'affixe

$z_{M}=z=x+\mathrm{i}y$ et

$M'\begin{pmatrix} x'\\ y' \end{pmatrix}$ d'affixe

$z_{M'}=z'=x'+\mathrm{i}y'.$

Donc,

$\begin{array}{rcl} z'&=&\dfrac{1}{5}(-3x+4y-12)+\dfrac{\mathrm{i}}{5}(4x+2y+6)\\ \\ &=&(x-\mathrm{i}y)\left(-\dfrac{3}{5}+\dfrac{4}{5}\mathrm{i}\right)-\dfrac{12}{5}+\dfrac{6}{5}\mathrm{i}\\ \\ \Rightarrow\ z'&=&\left(-\dfrac{3}{5}+\dfrac{4}{5}\mathrm{i}\right)\overline{z}-\dfrac{12}{5}+\dfrac{6}{5}\mathrm{i}\end{array}$

Cette dernière écriture traduit l'expression complexe de

$S_{(\Delta)}$ avec

$\overline{z}=x-\mathrm{i}y.$

II.3.4 Composée et réciproque

Soit

$S_{\Delta}$ une réflexion d'axe

${\Delta}$ . On a :

$(S_{\Delta})^{-1}=S_{\Delta}$

Supposons

$(\Delta_{1})//(\Delta_{2})$ et

$S_{\Delta_{1}}$ ,

$S_{\Delta_{2}}$ deux réflexions d'axes

$\Delta_{1}$ et

$\Delta_{2}$ respectivement. Alors, pour tout

$M$ , l'image

$M'$ , par leur composée est donnée par :

$S_{\Delta_{2}}\circ S_{\Delta_{1}}(M)=S_{\Delta_{2}}(S_{\Delta_{1}}(M))=S_{\Delta_{2}}(M_{1})=M'$

Nous avons :

$\begin{array}{rcl}\overrightarrow{MM'}&=&\overrightarrow{MM}_{1}+\overrightarrow{M_{1}M'}\\ \\ &=&2\overrightarrow{IM}_{1}+2\overrightarrow{M_{1}J}\\ \\ &=&2\left(\overrightarrow{IM}_{1}+\overrightarrow{M_{1}J}\right)\\ \\ &=&2\overrightarrow{IJ}\\ \\ \Rightarrow\ M'&=&t_{2\overrightarrow{IJ}}(M)\end{array}$

$I$ et

$J$ sont respectivement les points d'intersection de la droite perpendiculaire à

$\Delta_{1}$ et à

$\Delta_{2}$ passant par

$M$

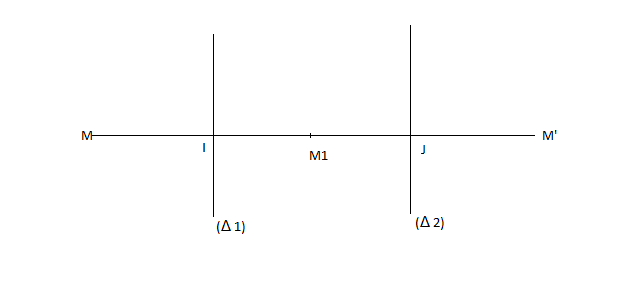
$S_{\Delta_{2}}\circ S_{\Delta_{1}}=t_{2\overrightarrow{IJ}}$

II.4 Rotation

II.4.1 Définition

Soient

$\theta\in\mathbb{R}$ et

$\Omega$ un point du plan. On appelle rotation d'angle

$\theta$ et de centre

$\Omega$ la transformation du plan notée

$r_{(\Omega,\ \theta)}$ qui laisse

$\Omega$ invariant et qui associe à tout point

$M$ de

$\mathcal{P}$ le point

$M'$ tel que

$\left\lbrace\begin{array}{lcl}\Omega M &=& \Omega M' \\\left(\overrightarrow{\Omega M},\ \overrightarrow{\Omega M'}\right) &=& \theta\ (2\pi)\end{array}\right.\;,\quad\theta \neq 0(2\pi)$

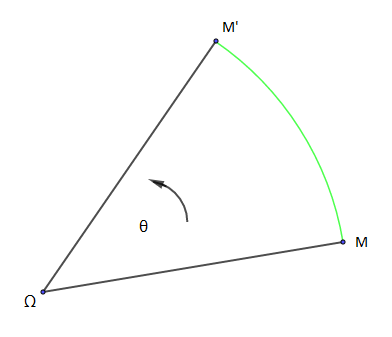
$\centerdot\ \$ si

$\theta=0(2\pi) \: \Longrightarrow \: r_{(\Omega,\ \theta)}=Id$

$\centerdot\ \$ si

$\theta=\pi(2\pi) \: \Longrightarrow \: r_{(\Omega,\ \theta)}=S_{\Omega}$

II.4.2 Points invariants

$\centerdot\ \$ InV

$r_{(\Omega,\ \theta)}=\{\Omega\}$ .

$\ \Omega$ est le seul point invariant.

$\centerdot\ \$

$ABCD$ carré direct alors

$r_{(O,\ \frac{\pi}{2})}$ ,

$\ r_{(O,\ \pi)}$ et

$r_{(O,\ -\frac{\pi}{2})}$ laissent globalement invariant le carré.

$\centerdot\ \$

$ABC$ triangle alors

$r_{(G,\ \frac{2\pi}{3})}$ et

$r_{(G,\ -\frac{2\pi}{3})}$ laissent globalement invariant le triangle

$ABC.$

II.4.3 Propriétés

$\centerdot\ \$

$r_{(\Omega,\ \theta)}$ conserve le barycentre, les distances et les angles orientés. Donc, une rotation est un déplacement.

$\centerdot\ \$

$r_{(\Omega,\ \theta)}$ conserve le parallélisme, la perpendiculaire et l'alignement.

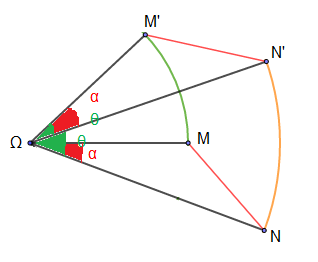
On a :

$\begin{eqnarray} M'N'^{2}&=&\Omega M'^{2}+\Omega N'^{2}-2\Omega N'.\Omega M'.cos\alpha\nonumber \\ \\&=&\Omega M^{2}+\Omega N^{2}-2\Omega N.\Omega M.\cos\alpha\nonumber\\ \\ \text{Donc }\ M'N'^{2}&=&MN^{2}\nonumber\\ \\ \Rightarrow\ M'N'&=&MN\nonumber \end{eqnarray}$

II.4.4 Expression complexe et analytique

Soient

$\Omega\begin{pmatrix} a\\ b\end{pmatrix}$ d'affixe

$z_{\Omega}=a+\mathrm{i}b=\alpha\$ ,

$\ M\begin{pmatrix} x\\ y\end{pmatrix}$ d'affixe

$z_{M}=z=x+\mathrm{i}y$ et

$M'\begin{pmatrix} x'\\ y'\end{pmatrix}$ d'affixe

$z_{M'}=z'=x'+\mathrm{i}y'$ .

On a :

$\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)=M'&\Leftrightarrow&\left\lbrace\begin{array}{rcl}\Omega M&=&\Omega M' \\ \left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}\right)&=&\theta (2\pi) \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\dfrac{\Omega M'}{\Omega M}&=&1 \\ \\ \left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}\right)&=&\theta (2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\left|\dfrac{z'-z_{\Omega}}{z-z_{\Omega}}\right|&=&1 \\ \\ arg\;\left(\dfrac{z'-z_{\Omega}}{z-z_{\Omega}}\right)&=&\theta (2\pi)\end{array}\right.\end{array}$

Donc

$\dfrac{z'-z_{\Omega}}{z-z_{\Omega}}=\mathrm{e}^{\mathrm{i}\theta} \: z'-z_{\Omega}=\mathrm{e}^{\mathrm{i}\theta}(z-z_{\Omega})$ ou

$z'=\mathrm{e}^{\mathrm{i}\theta}z+\beta$

Ainsi,

$z'=e^{\mathrm{i}\theta}z+\beta$ est l'expression complexe de la rotation d'angle

$\theta$ et de centre

$\Omega$ tels que

$z_{\Omega}=\mathrm{e}^{\mathrm{i}\theta}z_{\Omega}+\beta$ ,

$z_{\Omega}=\dfrac{\beta}{1-\mathrm{e}^{\mathrm{i}\theta}}$

Autrement, soit

$z'=\mathrm{e}^{\mathrm{i}\theta}z+\beta$ avec

$\beta=\beta_{1}+\beta_{2}$

On a :

$\begin{array}{rcl} x'+\mathrm{i}y'&=&(\cos\theta+\mathrm{i}\sin\theta)(x+\mathrm{i}y)+\beta_{1}+\beta_{2}\\ \\ &\Rightarrow&\left\lbrace\begin{array}{rcl} x'&=&x\cos\theta-y\sin\theta+\beta_{1} \\ y'&=&y\cos\theta+x\sin\theta+\beta_{2} \end{array}\right.\end{array}$

qui est l'expression analytique

II.4.5 Composée et réciproque

On a :

$\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)=M'&\Leftrightarrow&\left\lbrace\begin{array}{rcl}\Omega M&=&\Omega M'\\ \left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}\right)&=&\theta (2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\Omega M'&=&\Omega M\\ \left(\overrightarrow{\Omega M'}\;,\ \overrightarrow{\Omega M}\right)&=&-\theta (2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&M=r_{(\Omega\;,\ -\theta)}(M')=(r_{(\Omega\;,\ \theta)})^{-1}(M')\end{array}$

D'où,

$(r_{(\Omega\;,\ \theta)})^{-1}=r_{(\Omega\;,\ -\theta)}$ . La réciproque de la rotation de centre

$\Omega$ et d'angle

$\theta$ est la rotation de même centre

$\Omega$ et d'angle

$-\theta.$

$-\$ même centre :

Soient

$r_{1}$ et

$r_{2}$ deux rotations de même centre

$\Omega$ invariant.

On a :

$r_{1}=r_{(\Omega\;,\ \theta_{1})}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{1}}z+\alpha$

$r_{2}=r_{(\Omega\;,\ \theta_{2})}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta$

Soit

$r=r_{1}\circ r_{2}$ la composée de

$r_{1}$ et de

$r_{2}$ . On a :

$r=r_{1}\circ r_{2}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{1}}(\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta)+\alpha\ \Rightarrow\ z'=\mathrm{e}^{\mathrm{i}(\theta_{1}+\theta_{2})}z+\mathrm{e}^{\mathrm{i}\theta_{2}}\beta+\alpha$

$-\$ si

$\theta_{1}+\theta_{2}\neq 0(2\pi)$ , alors

$r_{1}\circ r_{2}$ est une rotation de centre

$\Omega$ et d'angle

$\theta=(\theta_{1}+\theta_{2}).$

$-\$ si

$\theta_{1}+\theta_{2}=0(2\pi)$ , alors

$\theta_{1}=-\theta_{2}$ et donc

$r_{2}=r_{\left(\Omega\;,\ \theta_{1}\right)}=\left(r_{\left(\Omega\;,\ \theta_{2}\right)}\right)^{-1}.$

D'où,

$r_{1}\circ r_{2}=Id$

$-\$ centres différents :

$r_{1}$ et

$r_{2}$ sont maintenant de centres différents. On a:

$r_{1}=r_{(\Omega_{1}\;,\ \theta_{1})}\ :\ z'-z_{\Omega_{1}}=\mathrm{e}^{\mathrm{i}\theta_{1}}(z-z_{\Omega_{1}})$ ou

$z'=\mathrm{e}^{\mathrm{i}\theta_{1}}z+\alpha$

$r_{2}=r_{(\Omega_{2}\;,\ \theta_{2})}\ :\ z'-z_{\Omega_{2}}=\mathrm{e}^{\mathrm{i}\theta_{2}}(z-z_{\Omega_{2}})$ ou

$z'=\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta$

Soit

$r=r_{1}\circ r_{2}$ la composée de

$r_{1}$ et de

$r_{2}$ . On a :

$r=r_{1}\circ r_{2}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{1}}(\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta)+\alpha$

Donc,

$M'$ est d'affixe

$z'=\mathrm{e}^{\mathrm{i}(\theta_{1}+\theta_{2}}z+\delta$

$-\$ si

$\theta_{1}+\theta_{2}\neq 0(2\pi)\ \Rightarrow\ r_{1}\circ r_{2}$ est une rotation de centre

$\Omega$ tel que

$z_{\Omega}=\dfrac{\delta}{1-\mathrm{e}^{\mathrm{i}(\theta_{1}+\theta_{2})}}$ et d'angle

$\theta=(\theta_{1}+\theta_{2}).$

$-\$ si

$\theta_{1}+\theta_{2}=0(2\pi)\ \Rightarrow\ r_{1}\circ r_{2}$ est une translation de vecteur

$\vec{u}(\delta)$

$-\$ composée d'une rotation

$r_{(\Omega\;,\ \theta)}$ et d'une translation de vecteur

$\vec{u}(\delta)$ :

Soient

$r_{1}$ une rotation et

$t$ une translation de vecteur, définies respectivement par :

$r_{1}=r_{(\Omega\;,\ \theta)}$ ;

$z'=\mathrm{e}^{\mathrm{i}\theta}z+\beta$ et

$t_{\vec{u}}$ ;

$z'=z+\alpha$

Considérons la composée

$r=r_{1}\circ t$ définie par :

$r=r_{(\Omega\;,\ \theta)}\circ t_{\vec{u}}\;;\ z'=\mathrm{e}^{\mathrm{i}\theta}(z+\alpha)+\beta$ ou encore

$z'=\mathrm{e}^{\mathrm{i}\theta}z+\delta$

$z'=\mathrm{e}^{\mathrm{i}\theta}z+\delta$ est l'expression complexe d'une rotation. Donc la composée d'une rotation et d'une translation est une rotation d'angle ; l'angle de la rotation et de centre ; le point invariant.

II.4.6 Décomposition d'une rotation

$\centerdot\ \$ composée de deux symétries axiales d'axes sécants :

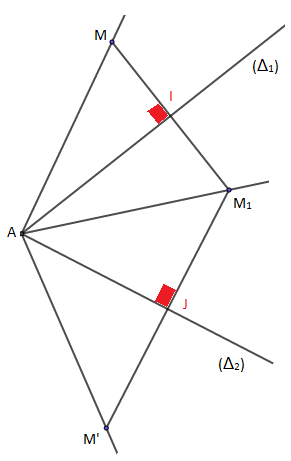
Soit

$A$ le point d'intersection entre

$\Delta_{1}$ et

$\Delta_{2}$ ; on a :

$S_{\Delta_{2}}\circ S_{\Delta_{1}}(M)=S_{\Delta_{2}}(S_{\Delta_{1}}(M))=S_{\Delta_{2}}(M_{1})=M'$

De plus

$AM=AM_{1}=AM'$

$\begin{eqnarray}\left(\overrightarrow{AM}\;,\ \overrightarrow{AM'}\right)&=&\left(\overrightarrow{AM}\;,\ \overrightarrow{AM_{1}}\right)+\left(\overrightarrow{AM_{1}}\;,\ \overrightarrow{AM'}\right)\nonumber\\ \\ &=&2\left(\overrightarrow{AI}\;,\ \overrightarrow{AM_{1}}\right)+2\left(\overrightarrow{AM_{1}}\;,\ \overrightarrow{AJ}\right)\nonumber\\ \\ \Rightarrow\ \left(\overrightarrow{AM}\;,\ \overrightarrow{AM'}\right)&=&2\left(\overrightarrow{AI}\;,\ \overrightarrow{AJ}\right)\nonumber \end{eqnarray}$

Donc

$S_{\Delta_{2}}\circ S_{\Delta_{1}}(M)=M'\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} AM&=&AM'\\ \left(\overrightarrow{AM}\;,\ \overrightarrow{AM'}\right)&=&2\left(\overrightarrow{AI}\;,\ \overrightarrow{AJ}\right)(2\pi)\end{array}\right.$

Ce qui se traduit par :

$M'=r_{[A\;,\ 2(\overrightarrow{AI}\;,\ \overrightarrow{AJ})]}(M)$

D'où, la composée

$S_{\Delta_{2}}\circ S_{\Delta_{1}}$ de deux réflexions d'axes sécants en

$A$ est une rotation de centre

$A$ et d'angle

$2\left(\widehat{\Delta_{1}\;,\ \Delta_{2}}\right)(2\pi)$

Toute rotation

$r$ de centre

$\Omega$ et d'angle

$\theta$ peut se décomposer en une composée de symétries axiales d'axes

$(\Delta_{1})$ et

$(\Delta_{2})$ sécants en

$\Omega$ ; le centre de la rotation est tel que

$2\left(\widehat{\Delta_{1}\;,\ \Delta_{2}}\right)=\theta\;;\ (r=S_{\Delta_{2}}\circ S_{\Delta_{1}}).$

III Isométrie

III.1 Définition

Une isométrie du plan est une transformation qui conserve les distances,

$\forall M$ et

$N$ tels que

$f(M)=M'$ et

$f(N)=N'$ alors

$M'N'=MN.$

III.2 Classification des isométries

$\centerdot\ \$ une isométrie

$f$ qui fixe trois points

$A$ ,

$\ B$ et

$C$ non alignés est l'identité.

$\centerdot\ \$ une isométrie

$f$ qui fixe deux points

$A$ et

$B$ , si elle est différente de l'identité, est une symétrie axiale d'axe

$(AB)$ .

$\centerdot\ \$ une isométrie

$f$ qui a un seul point invariant

$\Omega$ est une rotation de centre

$\Omega$

Exercice d'application

Soit

$f$ l'application définie par

$\left\lbrace\begin{array}{rcl} x'&=&\dfrac{1}{2}\left(x+y\sqrt{3}+1\right) \\ \\ y'&=&\dfrac{1}{2}\left(-x\sqrt{3}+y+\sqrt{3}\right)\end{array}\right.$ qui, à tout

$M\begin{pmatrix} x \\ y\end{pmatrix}$ , associe le point

$M'\begin{pmatrix} x' \\ y'\end{pmatrix}$

a) Montrer que

$f$ est une isométrie

b) Déterminer InV

$f$ , en déduire que

$f$ est une rotation dont on précisera le centre et l'angle.

Résolution

a) Soient

$M_{1}\begin{pmatrix} x_{1} \\ y_{1}\end{pmatrix}$ et

$M_{2}\begin{pmatrix} x_{2} \\ y_{2}\end{pmatrix}$ deux points du plan d'images respectives

$M'_{1}\begin{pmatrix} x_{1}' \\ y_{1}'\end{pmatrix}$ et

$M_{2}'\begin{pmatrix} x_{2}' \\ y_{2}'\end{pmatrix}$ , alors

$\begin{array}{rcl} ||\overrightarrow{M_{1}'M_{2}'}||^{2}&=&(x_{2}'-x_{1}')^{2}+(y_{2}'-y_{1}')^{2}\\ \\ &=&\dfrac{1}{4}\left(x_{2}+y_{2}\sqrt{3}+1-x_{1}-y_{1}\sqrt{3}-1\right)^{2}+\\ \\ & &\dfrac{1}{4}\left(-x_{2}\sqrt{3}+y_{2}+\sqrt{3}+x_{1}\sqrt{3}-y_{1}-\sqrt{3}\right)^{2}\\ \\ &=&\dfrac{1}{4}\left((x_{2}-x_{1})+\sqrt{3}(y_{2}-y_{1})\right)^{2}+\dfrac{1}{4}\left(-\sqrt{3}(x_{2}-x_{1})+(y_{2}-y_{1})\right)^{2}\\ \\ &=&\dfrac{1}{4}\left((x_{2}-x_{1})^{2}+3(y_{2}-y_{1})^{2}+3(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}\right)\\ \\ &=&\dfrac{1}{4}\left(4(x_{2}-x_{1})^{2}+4(y_{2}-y_{1})^{2}\right)\\ \\ &=&(x_{2}-x_{1})^{2}+4(y_{2}-y_{1})^{2}\\ \\ &=&||\overrightarrow{M_{1}M_{2}}||^{2}\end{array}$

Donc,

$||\overrightarrow{M_{1}'M_{2}'}||^{2}=||\overrightarrow{M_{1}M_{2}}||^{2}\ \Rightarrow\ M_{1}'M_{2}'=M_{1}M_{2}$ , ce qui montre bien que

$f$ est une isométrie.

$\begin{array}{rcl} M\in\text{InV}f&\Leftrightarrow&f(M)=M\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&x \\ y'&=&y\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&\dfrac{1}{2}\left(x+y\sqrt{3}+1\right) \\ \\ y&=&\dfrac{1}{2}\left(-x\sqrt{3}+y+\sqrt{3}\right)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\dfrac{1}{2}\left(-x+y\sqrt{3}+1\right)&=&0 \\ \\ \dfrac{1}{2}\left(-x\sqrt{3}-y+\sqrt{3}\right)&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} -x+y\sqrt{3}+1&=&0 \\ -x\sqrt{3}-y+\sqrt{3}&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&1 \\ y&=&0\end{array}\right.\end{array}$

Donc, InV

$f=\Omega\begin{pmatrix} 1 \\ 0\end{pmatrix}$

$f$ est une isométrie qui a un seul point invariant

$\Omega$ , donc,

$f$ est une rotation de centre

$\Omega$ d'affixe 1.

Soit

$z=x+\mathrm{i}y$ l'affixe de

$M$ et

$z'=x'+\mathrm{i}y'$ celui de

$M'$ , alors

$\begin{array}{rcl} z'&=&x'+\mathrm{i}y' \\ \\&=&\dfrac{1}{2}\left(x+y\sqrt{3}+1\right)+\dfrac{\mathrm{i}}{2}\left(-x\sqrt{3}+y+\sqrt{3}\right)\\ \\ &=&x\left(\dfrac{1}{2}-\dfrac{\mathrm{i}\sqrt{3}}{2}\right)+y\left(\dfrac{\sqrt{3}}{2}+\dfrac{\mathrm{i}}{2}\right)+\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}\\ \\ &=&(x+\mathrm{i}y)\left(\dfrac{1}{2}-\dfrac{\mathrm{i}\sqrt{3}}{2}\right)+\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}\\ \\ &=&\left(\dfrac{1}{2}-\dfrac{\mathrm{i}\sqrt{3}}{2}\right)z+\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}\end{array}$

Donc,

$z'=\mathrm{e}^{-\mathrm{i}\tfrac{\pi}{3}}z+b$ avec

$b=\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}$ . Ainsi,

$f$ est une rotation de centre

$\Omega$ et d'angle

$\theta=-\dfrac{\pi}{3}.$

III.3 Propriétés

$\centerdot\ \$ La réciproque d'une isométrie est une isométrie.

$\centerdot\ \$ La composée d'une isométrie est une isométrie.

$\centerdot\ \$ Une isométrie conserve le barycentre, le produit scalaire, l'alignement, le parallélisme, la perpendiculaire. L'image d'une figure quelconque est une figure de même nature et de même dimension.

$\centerdot\ \$ Une isométrie qui conserve la mesure des angles orientés est appelée déplacement et celle qui change les signes des angles orientés est appelée antidéplacement.

III.4 Décomposition d'une isométrie

Soit

$f$ une isométrie telle que

$f(A)=A'$ . Posons

$t$ la translation de vecteur

$\overrightarrow{A'A}$ ;

$t=t_{\overrightarrow{A'A}}$ et

$f_{1}=t\circ f$ est une isométrie.

Nous avons

$f_{1}(A)=t\circ f(A)=t[f(A)]=t(A')=A$ . Donc

$f_{1}$ est une isométrie qui fixe

$A$ .

$f_{1}=t\circ f \: \Rightarrow \: t^{-1}\circ f_{1}=f$ où

$t^{-1}=t_{\overrightarrow{AA'}}$ .

Ainsi, toute isométrie

$f$ peut se décomposer en une composition d'une translation et d'une isométrie qui fixe un point.

Théorème :

Etant donnés quatre points

$A$ ,

$\ B$ ,

$\ C$ et

$D$ tels que

$AB=CD$ , il existe une isométrie et une seule qui transforme

$A$ en

$C$ et

$B$ en

$D$ .

$\overrightarrow{AB}=\overrightarrow{CD}$ alors l'isométrie est la translation de vecteur

$\overrightarrow{AC}$ .

$\overrightarrow{AB}\neq\overrightarrow{CD}$ alors l'isométrie est une rotation dont le centre est le point de rencontre des médiatrices de

$[BC]$ et de

$[BA]$ et d'angle

$\theta=\left(\widehat{\overrightarrow{AB},\ \overrightarrow{CD}}\right)$ car

$\begin{eqnarray} \left\lbrace\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)&=&M'\\ r_{(\Omega\;,\ \theta)}(N)&=&N' \end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} MN&=&M'N'\\ \left(\overrightarrow{MN}\;,\ \overrightarrow{M'N'}\right)&=&\theta (2\pi) \end{array} \right.\nonumber \end{eqnarray}$

Auteur:

Seyni Ndiaye & Diny Faye

Commentaires

Anonyme (non vérifié)

dim, 03/20/2022 - 15:45

Permalien

Bien fait.. mais est-ce que

Bien fait.. mais est-ce que le cours pourrais être enseigner comme sa où il y a des modifications à faire

répondre

Anonyme (non vérifié)

dim, 03/20/2022 - 15:46

Permalien

Bien fait

Email:

lomassamba7@gmail.com

répondre

Kirikou (non vérifié)

dim, 07/21/2024 - 17:02

Permalien

suggestion

Cours bien fait mais est que le format pdf est disponible

Email:

thiaremood@gmail.com

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Transformations - Isométries du plan - T S1

Formulaire de recherche

I Définitions

Exemple :

II Exemples

II.1 Translation

II.1.1 Définitions

II.1.2 Ensembles invariants

II.1.3 Propriétés

II.1.4 Expression complexe et analytique

II.1.5 Composée et réciproque

Exercice d'application

Résolution

II.2 Homothéties

II.2.1 Définitions

II.2.2 Ensembles invariants

II.2.3 Propriétés

II.2.4 Expression analytique et complexe

Exercice d'application

Résolution

II.2.5 Composée et réciproque

II.3 Réflexion

II.3.1 Définition

II.3.2 Propriétés

II.3.3 Expression analytique et complexe

II.3.4 Composée et réciproque

II.4 Rotation

II.4.1 Définition

II.4.2 Points invariants

II.4.3 Propriétés

II.4.4 Expression complexe et analytique

II.4.5 Composée et réciproque

II.4.6 Décomposition d'une rotation

III Isométrie

III.1 Définition

III.2 Classification des isométries

Exercice d'application

Résolution

III.3 Propriétés

III.4 Décomposition d'une isométrie

Théorème :

Commentaires

Bien fait.. mais est-ce que

Bien fait

suggestion

Ajouter un commentaire

Plain text