Transformations - Isométries du plan - T S1
I Définitions
On appelle transformation du plan toute application bijective du plan dans lui-même.
$f$ est une transformation du plan $\mathcal{P}$ si $\forall\;M\in\mathcal{P}$, $\exists$ un unique point $N$ tel que $f(N)=N.$
Exemple :
translation , homothéties, symétries, rotation, affinités
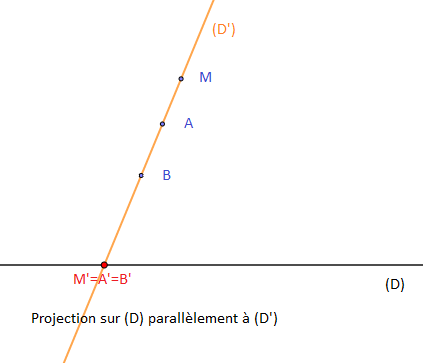
La projection n'est pas une transformation
II Exemples
II.1 Translation
II.1.1 Définitions
Soit $\vec{u}$ un vecteur non nul.
On appelle translation de vecteur $\vec{u}$ la transformation du plan notée $t_{\vec{u}}$ qui associe, à tout point $M$ de $\mathcal{P}$, le point $M'$ tel que $\overrightarrow{MM'}=\vec{u}$.
II.1.2 Ensembles invariants
$\centerdot\ \ $ Un point $M$ est invariant par une transformation $f$ si $\ f(M)=M$. L'ensemble des points invariants est noté InV$f$.
$\centerdot\ \ $ Un ensemble $E$ est dit globalement invariant par une transformation $f$ si $\ f(E)=E$.
$\centerdot\ \ $ InV$t_{\vec{u}}=\emptyset$
$\centerdot\ \ $ Toute droite de direction $\vec{u}$ est globalement invariant par $t_{\vec{u}}$
II.1.3 Propriétés
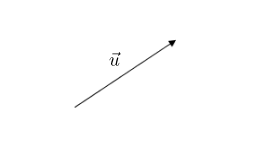
$\centerdot\ \ $ Propriété caractéristique : soient $M\ $ et $\ N$ deux points du plan d'images respectives $M'\ $ et $\ N'$ par $t_{\vec{u}}$.
Nous avons $t_{\vec{u}}(M)=M'$ si, et seulement si, $\overrightarrow{MM'}=\vec{u}$
De même $t_{\vec{u}}(N)=N'$ si, et seulement si, $\overrightarrow{NN'}=\vec{u}$
Ce qui entraine : $\overrightarrow{MM'}=\overrightarrow{NN'}$
D'où, $(MM'N'N)$ est un parallélogramme
$\centerdot\ \ $ Une transformation $f$ conserve le barycentre si pour $G$ barycentre de $(A_{i},\ \alpha_{i})_{1\leq i\leq n}$ alors $f(G)$ est barycentre de $(f(A_{i}),\ \alpha_{i})_{1\leq i\leq n}$
Si $G$ est barycentre de $(A,\ \alpha)$, $\ (B,\ \beta)$, $\ (C,\ \gamma)$ avec $\alpha + \beta + \gamma \neq 0$ alors, $\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}=\vec{0}$
Ainsi, si $t_{\vec{u}}(G)=G'$, $\ t_{\vec{u}}(A)=A'$, $\ t_{\vec{u}}(B)=B'$ et $t_{\vec{u}}(C)=C'$ alors
$\overrightarrow{G'A'}=\overrightarrow{GA}$,$\ $ $\overrightarrow{G'B'}=\overrightarrow{GB}$ et $\overrightarrow{G'C'}=\overrightarrow{GC}$
Et par suite, $\alpha\overrightarrow{G'A'}+\beta\overrightarrow{G'B'}+\gamma\overrightarrow{G'C'}=\vec{0}$ avec $\alpha + \beta + \gamma \neq 0$
Donc, $G'$ est barycentre de $(A',\ \alpha)$, $\ (B',\ \beta)$, $\ (C',\ \gamma)$
La translation conserve le barycentre. Elle conserve aussi le produit scalaire.
$\centerdot\ \ $ $t_{\vec{u}}(M)=M'$ et $t_{\vec{u}}(N)=N'$ alors $\overrightarrow{M'N'}=\overrightarrow{MN}$
Ce qui donne, $||\overrightarrow{M'N'}||=||\overrightarrow{MN}||$
Ainsi, la translation du vecteur $\vec{u}$ conserve la distance.
Une transformation du plan qui conserve la distance est appelée une isométrie. Donc la translation est une isométrie.
$\centerdot\ \ $ Soient trois points $A$ , $\ B$ et $C$ d'images respectives $A'$ , $\ B'$ et $C'$ par $t_{\vec{u}}$ ; $\overrightarrow{A'B'}=\overrightarrow{AB}$ et $\overrightarrow{A'C'}=\overrightarrow{AC}$ alors on a : $\left(\overrightarrow{AB},\ \overrightarrow{AC}\right)=\left(\overrightarrow{A'B'},\ \overrightarrow{A'C'}\right)$
Donc, la translation de vecteur $\vec{u}$ conserve les angles orientés.
Une transformation du plan qui conserve les distances et la angles orientés est appelée un déplacement.
Donc une translation est un déplacement.
$\centerdot\ \ $ $t_{\vec{u}}(M)=M'$ et $t_{\vec{u}}(N)=N'$ $\Longrightarrow \: \overrightarrow{M'N'}=\overrightarrow{MN}$
Donc, $\overrightarrow{M'N'}$ et $\overrightarrow{MN}$ sont colinéaires.
D'où, l'image d'une droite est une droite qui lui est parallèle.
En conclusion la translation conserve :
$\centerdot\ \ $ l'alignement
$\centerdot\ \ $ le parallélisme
$\centerdot\ \ $ l'orthogonalité
$\centerdot\ \ $ le barycentre
$\centerdot\ \ $ les distances
$\centerdot\ \ $ les angles orientés
Aussi, l'image d'une figure quelconque est une figure de même nature.
II.1.4 Expression complexe et analytique
Soient $\vec{u}\begin{pmatrix} a\\b\end{pmatrix}$ ; $\ z_{\vec{u}}=a+ib$. $\ M\begin{pmatrix} x\\y \end{pmatrix}$ et $M'\begin{pmatrix} x'\\y'\end{pmatrix}$ ; $\ t_{\vec{u}}(M)=M'$.
$M$ d'affixe $z$ noté $M(z)\;;\ z=x+\mathrm{i}y$ et $M'$ d'affixe $z'$ noté $M'(z')\;;\ z'=x'+\mathrm{i}y'$
On a : \begin{eqnarray} \overrightarrow{MM'}=\vec{u}&\Leftrightarrow&z_{\overrightarrow{MM'}}=z_{\vec{u}}\nonumber \\ \\&\Leftrightarrow&z-z'=z_{\vec{u}}\nonumber \\ \\&\Leftrightarrow&z'=z+z_{\vec{u}}\nonumber \end{eqnarray}
$z'=z+\alpha$ est l'expression complexe d'une translation de vecteur $\vec{u}(\alpha)$ avec $\alpha=z_{\vec{u}}$
Nous avons : \begin{eqnarray} z'=z+z_{\vec{u}}\ \Rightarrow\ x'+\mathrm{i}y'&=&x+\mathrm{i}y+a+ib\nonumber \\ \\&=&x+a+\mathrm{i}(y+b)\nonumber \end{eqnarray}
Ainsi, $\left\lbrace\begin{array}{lcl} x'&=&x+a \\ y'&=&y+b\end{array}\right.$ est l'expression analytique d'une translation.
II.1.5 Composée et réciproque
Soit $t$ une translation, $M$ un point du plan d'image $M'$ par $t$.
On a : $t_{\vec{0}}=Id$.
En effet, $t_{\vec{0}}(M)=M'$ si et seulement si $\overrightarrow{MM'}=\vec{0}$. Donc $M=M'$
Soient deux vecteurs $\vec{u}$ et $\vec{v}$ non nuls alors $t_{\vec{u}}\circ t_{\vec{v}}=t_{\vec{u}+\vec{v}}$
Et donc, $t_{\vec{u}}\circ t_{\vec{v}}(M)=t_{\vec{u}}[t_{\vec{v}}(M)]=t_{\vec{u}}(M_{1})=M'$
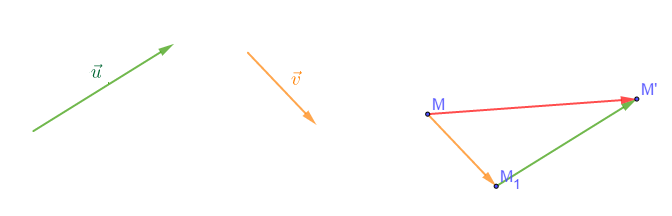
En effet, $t_{\vec{v}}(M)=M_{1}$, $\ t_{\vec{u}}(M_{1})=M'$
$\overrightarrow{MM'}=\overrightarrow{MM}_{1}+\overrightarrow{M_{1}M'}=\vec{u}+\vec{v}$
Donc, $t_{\vec{u}}\circ t_{\vec{v}}=t_{\vec{u}+\vec{v}}$
Soient $\vec{u}(\alpha)$ et $\vec{v}(\beta)$ deux vecteurs d'affixes respectifs $\alpha$ et $\beta$
On a : $t_{\vec{u}}$ : $z'=z+\alpha$ et $t_{\vec{v}}$ : $z'=z+\beta$
Alors, la composée $t_{\vec{u}}\circ t_{\vec{v}}$ sera définie par : $z'=z+\beta+\alpha$ avec $\beta+\alpha$ affixe de $\vec{u}+\vec{v}$
$t_{\vec{u}}$ une translation de vecteur $\vec{u}$ alors on a :
\begin{eqnarray} t_{\vec{u}}(M)=M'&\Leftrightarrow&\overrightarrow{MM'}=\vec{u}\nonumber \\ \\&\Leftrightarrow&\overrightarrow{M'M}=-\vec{u}\nonumber \\ \\&\Leftrightarrow&M=t_{-\vec{u}}(M')\nonumber \end{eqnarray}
Donc, $\left(t_{\vec{u}}\right)^{-1}=t_{-\vec{u}}$
La réciproque de la translation de vecteur $\vec{u}$ est la translation de vecteur $-\vec{u}.$
Exercice d'application
Soit $f$ l'application qui, à tout $M\begin{pmatrix} x \\ y\end{pmatrix}$, associe le point $M'\begin{pmatrix} x' \\ y'\end{pmatrix}$ tels que $$\left\lbrace\begin{array}{rcl} x'&=&x-2 \\ y'&=&y+1\end{array}\right.$$
1) Déterminer InV$f$
2) Montrer que $f$ est une translation de vecteur $\vec{u}$ dont on donnera les éléments caractéristiques.
3) Déterminer les images de $A\begin{pmatrix} 1 \\ 2\end{pmatrix}\;,\ C\left(B\begin{pmatrix} 0 \\ 3\end{pmatrix}\;;\ 5\right)\ $ et $\ D\ :\ y-2x+1=0$
4) Donner l'expression complexe
Résolution
1) \begin{eqnarray} M\in\text{InV}f&\Leftrightarrow&f(M)=M\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&x \\ y'&=&y\end{array}\right.\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&x-2 \\ y&=&y+1\end{array}\right.\quad\text{impossible}\nonumber \end{eqnarray}
Donc, InV$f=\emptyset$
2) Soit $M'\begin{pmatrix} x' \\ y'\end{pmatrix}$ image de $M\begin{pmatrix} x \\ y\end{pmatrix}$ par $f\;;\ \overrightarrow{MM}'\begin{pmatrix} x'-x \\ y'-y\end{pmatrix}$, alors \begin{eqnarray} f(M)=M'&\Rightarrow&\left\lbrace\begin{array}{rcl} x'&=&x-2 \\ y'&=&y+1\end{array}\right.\nonumber \\ \\&\Rightarrow&\left\lbrace\begin{array}{rcl} x'-x&=&-2 \\ y'-y&=&1\end{array}\right.\nonumber\\ \\ &\Rightarrow&\overrightarrow{MM}'\begin{pmatrix} x'-x \\ y'-y\end{pmatrix}=\vec{\omega}\begin{pmatrix} -2 \\ 1\end{pmatrix}\nonumber \end{eqnarray}
Soit $\vec{u}=\vec{\omega}$, alors $f$ est une translation de vecteur $\vec{u}=-2\vec{i}+\vec{j}$
3) \begin{eqnarray} \text{Soit }\ A'=t_{\vec{u}}(A)\;,\text{ alors }\left\lbrace\begin{array}{rcl} x_{A'}&=&x_{A}-2 \\ y_{A'}&=&y_{A}+1\end{array}\right.&\Rightarrow&\left\lbrace\begin{array}{rcl} x_{A'}&=&1-2 \\ y_{A'}&=&2+1\end{array}\right.\nonumber \\ \\&\Rightarrow&A'\begin{pmatrix} -1 \\ 3\end{pmatrix}\nonumber \end{eqnarray}
On a : $t_{\vec{u}}(C)=C'(B'\;;\ 5)$.
Soit $B'=t_{\vec{u}}(B)$, alors $\left\lbrace\begin{array}{rcl} x_{B'}&=&x_{B}-2 \\ y_{B'}&=&y_{B}+1\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{rcl} x_{B'}&=&-2 \\ y_{B'}&=&4\end{array}\right.$
Donc, $C'\left(B'\begin{pmatrix} -2 \\ 4\end{pmatrix}\;;\ 5\right)$
Soit $D'=t_{\vec{u}}(D)$ alors, $D'//D$ et donc, $D'\ :\ y-2x+c=0$
Déterminons la constante $c$
Soit $E\begin{pmatrix} 0 \\ -1\end{pmatrix}\in D$ alors, $t_{\vec{u}}(E)=E'\begin{pmatrix} x' \\ y'\end{pmatrix}\in D'.$
On a : $\left\lbrace\begin{array}{rcl} x_{E'}&=&x_{E}-2 \\ y_{E'}&=&y_{E}+1\end{array}\right.\ \Rightarrow\ E'\begin{pmatrix} -2 \\ 0\end{pmatrix}$
$E'\in D'$, alors $4+c=0\ \Rightarrow\ c=-4$. Donc $D'\ :\ y-2x-4=0$
4) Soit $z=x+\mathrm{i}y$ l'affixe de $M$ et $z'=x'+\mathrm{i}y'$ celui de $M'$, alors \begin{eqnarray} z'&=&x'+\mathrm{i}y'\nonumber \\ \\&=&x-2+\mathrm{i}(y+1)\nonumber \\ \\&=&x+\mathrm{i}y-2+\mathrm{i}\nonumber\\ \\ &=&z-2+\mathrm{i}\nonumber \end{eqnarray}
Donc, $z'=z-2+\mathrm{i}$ est l'expression complexe de cette transformation.
II.2 Homothéties
II.2.1 Définitions
Soit $\Omega$ un point du plan , $k \in\mathbb{R}^{*}\setminus \{1\}$. On appelle homothétie de centre $\Omega$ et de rapport $k$ la transformation du plan notée $h_{(\Omega,\ k)}$ qui laisse $\Omega$ invariant et qui associe à tout point $M$ différent de $\Omega$ le point $M'$ tel que $\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$
$h_{(\Omega,\ k)}(M)=M' \: \Leftrightarrow \: \overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$
II.2.2 Ensembles invariants
$\centerdot\ \ $ InV$h_{(\Omega,\ k)}=\{\Omega\}$. $\ \Omega$ est ici le seul point invariant.
Soit $M \in$ InV$h_{(\Omega,\ k)}$
Nous avons : $h_{(\Omega,\ k)}(M)=M$ si, et seulement si, $\overrightarrow{\Omega M}=k\overrightarrow{\Omega M}$
Ce qui donne : $\overrightarrow{\Omega M}(1-k)=\vec{0}$ or $1-k\neq 0$
Et donc, $\overrightarrow{\Omega M}=\vec{0}$. D'où, $\Omega=M$
$\centerdot\ \ $ Toute droite passant par $\Omega$ est globalement invariant par $h_{(\Omega,\ k)}$ car $\Omega$, $\ M$ et $M'$ alignés.
II.2.3 Propriétés
$\centerdot\ \ $ $h_{(\Omega,\ k)}(M)=M' \: \Longrightarrow \: \Omega, \; M, \; M'$ alignés.
$\centerdot\ \ $ $h_{(\Omega,\ k)}(M)=M'$ alors $\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$
$h_{(\Omega,\ k)}(N)=N'$ alors, $\overrightarrow{\Omega N'}=k\overrightarrow{\Omega N}$
Ce qui entraine $\overrightarrow{M'N'}=k\overrightarrow{MN}$
$\centerdot\ \ G$ barycentre de $(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$, alors $\alpha_{1}\overrightarrow{GA}_{1}+\alpha_{2}\overrightarrow{GA}_{2}+\ldots+\alpha_{n}\overrightarrow{GA}_{n}=\vec{0}.$
\begin{eqnarray} h_{(\Omega, k)}(G)=G'\text{ et }h_{(\Omega, k)}(A_{i})=A_{i}'&\Rightarrow&\overrightarrow{G'A'_{i}}=k\overrightarrow{GA_{i}}\nonumber\\ \\ &\Rightarrow&k\alpha_{1}\overrightarrow{GA}_{1}+k\alpha_{2}\overrightarrow{GA}_{2}+\ldots+k\alpha_{n}\overrightarrow{GA}_{n}=\vec{0}\nonumber\\ \\ &\Rightarrow&\alpha_{1}\overrightarrow{G'A'}_{1}+\alpha_{2}\overrightarrow{G'A'}_{2}+\ldots+\alpha_{n}\overrightarrow{G'A'}_{n}=\vec{0}\nonumber \end{eqnarray}
Ce qui montre que $G'$ est aussi barycentre de $(A_{i},\ \alpha_{i})_{1\leq i\leq n}$
Donc, il y a conservation du barycentre d'où, l'image d'une droite est une droite qui lui est parallèle car $\overrightarrow{M'N'}$ colinéaire à $\overrightarrow{MN}$
$\centerdot\ \ $ $\overrightarrow{M'N'}=k\overrightarrow{MN} \: \Rightarrow \: M'N'=|k|.MN$
Si $|k|\neq 1$ , la distance n'est pas conservée. L'homothétie de rapport $|k|\neq 1$ multiplie :
$\centerdot\ \ $ les distances par $|k|$
$\centerdot\ \ $ les aires par $k^{2}$
$\centerdot\ \ $ les volumes par $k^{3}$
$\centerdot\ \ $ soient $h_{(\Omega,\ k)}(A)=A'$, $h_{(\Omega,\ k)}(B)=B'$ et $h_{(\Omega,\ k)}(C)=C'$ alors on a :
\begin{eqnarray} \overrightarrow{A'B'}=k\overrightarrow{AB}\text{ et }\overrightarrow{A'C'}=k\overrightarrow{AC}\ \Rightarrow\ \left(\overrightarrow{A'B'}\;,\ \overrightarrow{A'C'}\right)&=&\left(k\overrightarrow{AB}\;,\ k\overrightarrow{AC}\right)\nonumber \\ &=&\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)\nonumber \end{eqnarray}
Donc, les angles orientés sont conservés.
L'homothétie conserve :
$\centerdot\ \ $ le barycentre
$\centerdot\ \ $ les angles orientés
$\centerdot\ \ $ la perpendiculaire
$\centerdot\ \ $ le parallélisme
L'image d'une figure quelconque est une figure de même nature.
II.2.4 Expression analytique et complexe
Soient $\Omega\begin{pmatrix} a\\ b \end{pmatrix}$ d'affixe $z_{\Omega}=a+\mathrm{i}b=\alpha\ $, $\ M\begin{pmatrix} x\\ y \end{pmatrix}$ d'affixe $z_{M}=z=x+\mathrm{i}y$ et $M'\begin{pmatrix} x'\\ y'\end{pmatrix}$ d'affixe $z_{M'}=z'=x'+\mathrm{i}y'.$
On a : \begin{eqnarray} h_{(\Omega\;,\ k)}(M)=M'&\Leftrightarrow&\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}\nonumber\\ \\ &\Leftrightarrow&z'-z_{\Omega}=k(z-z_{\Omega})\nonumber\\ \\ &\Leftrightarrow&z'=kz+(1-k)z_{\Omega}\nonumber \end{eqnarray}
Ainsi, $z'=kz+\beta$ est l'expression complexe d'une homothétie.
Autrement, \begin{eqnarray} z'-z_{\Omega}=k(z-z_{\Omega})&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'-a&=&k(x-a)\\ y'-b&=&k(y-b)\end{array}\right.\nonumber\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&kx+\alpha_{1}\\ y'&=&ky+\beta_{1}\end{array}\right.\nonumber \end{eqnarray} Ce dernier système détermine l'expression analytique d'une homothétie.
Exercice d'application
Soit $f$ l'application définie par $$\left\lbrace\begin{array}{rcl} x'&=&x-2 \\ y'&=&y+1\end{array}\right.$$ qui, à tout $M\begin{pmatrix} x \\ y\end{pmatrix}$, associe le point $M'\begin{pmatrix} x' \\ y'\end{pmatrix}$
1) Déterminer InV$f$
2) Montrer que $f$ est une homothétie dont on donnera les éléments caractéristiques.
3) Déterminer l'expression complexe
4) Déterminer les images de $O\begin{pmatrix} 0 \\ 0\end{pmatrix}\;,\ C\left(I\begin{pmatrix} 1 \\ 3\end{pmatrix}\;;\ 5\right)\ $ et $\ D\ :\ 2x-y+3=0$
Résolution
1) \begin{eqnarray} M\in\text{InV}f&\Leftrightarrow&f(M)=M\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&x \\ y'&=&y\end{array}\right.\nonumber\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&2x-1 \\ y&=&2y+3\end{array}\right.\nonumber \\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&1 \\ y&=&-3\end{array}\right.\nonumber \end{eqnarray}
Donc InV$f=\Omega\begin{pmatrix} 1 \\ -3\end{pmatrix}$
2) Soit $M'\begin{pmatrix} x' \\ y'\end{pmatrix}$ image de $M\begin{pmatrix} x \\ y\end{pmatrix}$ par $f$, alors \begin{eqnarray} \overrightarrow{\Omega M}'\begin{pmatrix} x'-1 \\ y'+3\end{pmatrix}&\Leftrightarrow&\begin{pmatrix} 2x-1-1 \\ 2y+3+3\end{pmatrix}\nonumber\\ \\ &\Leftrightarrow&\begin{pmatrix} 2x-2 \\ 2y+6\end{pmatrix}\nonumber\\ \\ &\Leftrightarrow&\begin{pmatrix} 2(x-1) \\ 2(y+3)\end{pmatrix}\quad\text{or }\ \overrightarrow{\Omega M}\begin{pmatrix} x-1 \\ y+3\end{pmatrix}\nonumber \\ \Rightarrow\ \overrightarrow{\Omega M}'&=&2\overrightarrow{\Omega M}\nonumber \end{eqnarray}
Soit $\overrightarrow{\Omega M}'=2\overrightarrow{\Omega M}$, donc $f$ est une homothétie de centre $\Omega$ et de rapport 2. Ainsi, $M'=h_{(\Omega\;,\ 2)}$
3) Soit $z=x+\mathrm{i}y$ l'affixe de $M$ et $z'=x'+\mathrm{i}y'$ celui de $M'$, alors
\begin{eqnarray} z'&=&x'+\mathrm{i}y'\nonumber \\ \\&=&2x-1+\mathrm{i}(2y+3)\nonumber\\ \\ &=&2x+2\mathrm{i}y-1+3\mathrm{i}\nonumber\\ \\ &=&2(x+\mathrm{i}y)-1+3\mathrm{i}\nonumber\\ \\ &=&2z-1+3\mathrm{i}\nonumber \end{eqnarray}
\begin{eqnarray} z'&=&x'+\mathrm{i}y'\nonumber \\ \\&=&2x-1+\mathrm{i}(2y+3)\nonumber\\ \\ &=&2x+2\mathrm{i}y-1+3\mathrm{i}\nonumber\\ \\ &=&2(x+\mathrm{i}y)-1+3\mathrm{i}\nonumber\\ \\ &=&2z-1+3\mathrm{i}\nonumber \end{eqnarray}
Donc, $z'=2z-1+3\mathrm{i}$ est l'expression complexe de cette transformation.
4) \begin{eqnarray} \text{Soit }\ O'=h_{(\Omega\;,\ 2)}(O)\;,\text{ alors }z_{O'}&=&2z_{O}-1+3\mathrm{i}\nonumber \\ \\&=&-1+3\mathrm{i}\nonumber \end{eqnarray}
Donc, $O'\begin{pmatrix} -1 \\ 3\end{pmatrix}$
On a : $h_{(\Omega\;,\ 2)}(C)=C'(I'\;;\ 10)$.
\begin{eqnarray} \text{Soit }\ I'=h_{(\Omega\;,\ 2)}(I)\;,\text{ alors }z_{I'}&=&2z_{I}-1+3\mathrm{i}\nonumber\\ \\ &=&2(1+3\mathrm{i})-1+3\mathrm{i}\nonumber\\ \\ &=&2+6\mathrm{i}-1+3\mathrm{i}\nonumber\\ \\ &=&1+9\mathrm{i}\nonumber \end{eqnarray}
Donc, $I'\begin{pmatrix} 1 \\ 9\end{pmatrix}$
Soit $D'=h_{(\Omega\;,\ 2)}(D)$, alors $D'//D$ et donc $D'\ :\ 2x-y+c=0.$
Déterminons la constante $c$
Soit $B\begin{pmatrix} 0 \\ 3\end{pmatrix}\in D$, alors \begin{eqnarray} B'=h_{(\Omega\;,\ 2)}(B)\ \Rightarrow\ z_{B'}&=&2z_{B}-1+3\mathrm{i}\nonumber\\ \\ &=&2(0+3\mathrm{i})-1+3\mathrm{i}\nonumber\\ \\ &=&6\mathrm{i}-1+3\mathrm{i}\nonumber\\ \\ &=&-1+9\mathrm{i}\nonumber \end{eqnarray}
Donc, $B'\begin{pmatrix} -1 \\ 9\end{pmatrix}\in D'$, alors $-2-9+c=0\ \Rightarrow\ c=11$. Donc $D'\ :\ 2x-y+11=0.$
II.2.5 Composée et réciproque
$\centerdot\ \ $
\begin{eqnarray} h_{(\Omega\;,\ k)}(M)=M'&\Rightarrow&\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}\nonumber\\ \\ &\Rightarrow&\overrightarrow{\Omega M}=\dfrac{1}{k}\overrightarrow{\Omega M'}\nonumber\\ \\ &\Rightarrow&M=h_{(\Omega\;,\ \frac{1}{k})}(M')\nonumber \end{eqnarray}
Donc, $\left(h_{(\Omega,\ k)}\right)^{-1}=h_{(\Omega,\ \frac{1}{k})}$
La réciproque d'une homothétie de centre $\Omega$ et de rapport $k$ est l'homothétie de centre $\Omega$ et de rapport $\dfrac{1}{k}$
$\centerdot\ \ $ Soient $h_{1}$ et $h_{2}$ deux homothéties de même centre $\Omega$ telles que $h_{1}=h_{(\Omega,\ k)}$ et $h_{2}=h_{(\Omega,\ k')}$
$\centerdot\ \ $ si $kk'=1$ alors $h_{1}\circ h_{2}=Id$.
$\centerdot\ \ $ si $kk'\neq 1$ alors $h_{1}\circ h_{2}=h_{(\Omega,\ kk')}$
$\centerdot\ \ $ $h_{1}$ et $h_{2}$ sont de centres différents ; $h_{1}=h_{(\Omega_{1},\ k_{1})}$ et $h_{2}=h_{(\Omega_{2},\ k_{2})}$.
On a : $h_{1}$ : $z'=k_{1}z+\alpha$ , $\ h_{2}$ : $z'=k_{2}z+\beta$
Donc, $h_{1}\circ h_{2}$ : $z'=k_{2}(k_{1}z+\alpha)+\beta=k_{2}k_{1}z+\alpha+\beta$
$\Rightarrow \: h_{1}\circ h_{2}\: : k_{2}k_{1}z+a$ avec $a=\alpha+\beta$
$\centerdot\ \ $ si $kk'=1$ alors $h_{1}\circ h_{2}$ est une translation.
$\centerdot\ \ $ si $kk'\neq 1$ alors $h_{1}\circ h_{2}$ est une homothétie de rapport $k_{1}k_{2}$ et de centre le point invariant.
$\centerdot\ \ $ Remarques : $h_{(\Omega,\ -1)}=S_{\Omega}$, car $\overrightarrow{\Omega M'}=-\overrightarrow{\Omega M}$ $\Longrightarrow \Omega$ est milieu de $[AB]$
II.3 Réflexion
II.3.1 Définition
Soit $\Delta$ une droite. On appelle réflexion d'axe $\Delta$ la transformation du plan qui laisse tout point de $\Delta$ invariant et qui associe à $M \notin\Delta$ le point $M'$ tel que $\Delta$ soit la médiatrice de $[AB].$
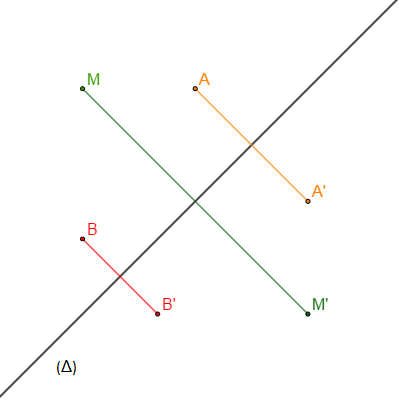
II.3.2 Propriétés
$\centerdot\ \ $ InV$S_{\Delta}=(\Delta)$
$\centerdot\ \ $ Toute perpendiculaire à $\Delta$ est globalement invariant par $S_{\Delta}$
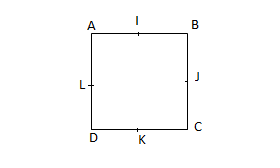
$\centerdot\ \ $ $ABCD$ un carré ; $S_{BD}$, $\ S_{AC}$, $\ S_{IK}$ et $S_{JL}$ laissent invariant le carré.
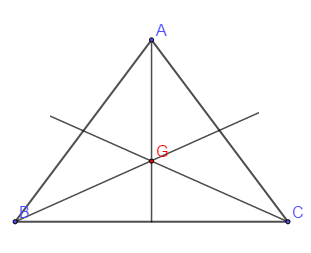
$\centerdot\ \ $ $ABC$ un triangle équilatérale ; $S_{AG}$, $\ S_{BG}$ et $S_{CG}$ laissent invariant le triangle ; $G$ isobarycentre de $ABC.$
$\centerdot\ \ $ La symétrie axiale conserve :
$\centerdot\ \ $ les angles consécutifs mais change le signe des angles orientés.
$\centerdot\ \ $ les distances
$\centerdot\ \ $ le parallélisme
La symétrie axiale est un antidéplacement ou isométrie négative. L'image d'une figure quelconque est une figure de même nature et de même dimension.
II.3.3 Expression analytique et complexe
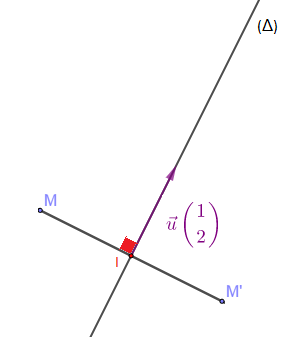
Soit $(\Delta)$ la droite d'équation : $2x-y+3=0$. On se donne $M\begin{pmatrix} x\\y\end{pmatrix}$ un point du plan d'image $M'\begin{pmatrix} x'\\y'\end{pmatrix}$ par la réflexion d'axe $(\Delta)$. Soient $\vec{u}\begin{pmatrix} 1\\2\end{pmatrix}$ vecteur directeur de $(\Delta)$ et $I\begin{pmatrix}\dfrac{x+x'}{2}\\ \\ \dfrac{y+y'}{2}\end{pmatrix}$ milieu de $[MM']$, donc $I\in\Delta$. On a :
$\begin{array}{rcl} S_{\Delta}(M)=M'&\Leftrightarrow&\overrightarrow{MM'}\cdot\vec{u}=\vec{0}\ \text{ et }\ I\in\Delta\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 1(x'-x)+2(y'-y)&=&0 \\ \\ 2\left(\dfrac{x+x'}{2}\right)-\left(\dfrac{y+y'}{2}\right)+3&=&0\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'+2y'-x-2y&=&0 \\ 2x'-y'+2x-y+6&=&0\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&\dfrac{1}{5}(-3x+4y-12) \\ \\ y'&=&\dfrac{1}{5}(4x+3y+6) \end{array}\right.\end{array}$
Ce dernier système définit une expression analytique de la réflexion $S_{\Delta}$.
En écriture complexe on a :
$M\begin{pmatrix} x\\ y \end{pmatrix}$ d'affixe $z_{M}=z=x+\mathrm{i}y$ et $M'\begin{pmatrix} x'\\ y' \end{pmatrix}$ d'affixe $z_{M'}=z'=x'+\mathrm{i}y'.$
Donc,
$\begin{array}{rcl} z'&=&\dfrac{1}{5}(-3x+4y-12)+\dfrac{\mathrm{i}}{5}(4x+2y+6)\\ \\ &=&(x-\mathrm{i}y)\left(-\dfrac{3}{5}+\dfrac{4}{5}\mathrm{i}\right)-\dfrac{12}{5}+\dfrac{6}{5}\mathrm{i}\\ \\ \Rightarrow\ z'&=&\left(-\dfrac{3}{5}+\dfrac{4}{5}\mathrm{i}\right)\overline{z}-\dfrac{12}{5}+\dfrac{6}{5}\mathrm{i}\end{array}$
Cette dernière écriture traduit l'expression complexe de $S_{(\Delta)}$ avec $\overline{z}=x-\mathrm{i}y.$
II.3.4 Composée et réciproque
Soit $S_{\Delta}$ une réflexion d'axe ${\Delta}$. On a :
$(S_{\Delta})^{-1}=S_{\Delta}$
Supposons $(\Delta_{1})//(\Delta_{2})$ et $S_{\Delta_{1}}$, $S_{\Delta_{2}}$ deux réflexions d'axes $\Delta_{1}$ et $\Delta_{2}$ respectivement. Alors, pour tout $M$, l'image $M'$, par leur composée est donnée par :
$S_{\Delta_{2}}\circ S_{\Delta_{1}}(M)=S_{\Delta_{2}}(S_{\Delta_{1}}(M))=S_{\Delta_{2}}(M_{1})=M'$
Nous avons :
$\begin{array}{rcl}\overrightarrow{MM'}&=&\overrightarrow{MM}_{1}+\overrightarrow{M_{1}M'}\\ \\ &=&2\overrightarrow{IM}_{1}+2\overrightarrow{M_{1}J}\\ \\ &=&2\left(\overrightarrow{IM}_{1}+\overrightarrow{M_{1}J}\right)\\ \\ &=&2\overrightarrow{IJ}\\ \\ \Rightarrow\ M'&=&t_{2\overrightarrow{IJ}}(M)\end{array}$
$I$ et $J$ sont respectivement les points d'intersection de la droite perpendiculaire à $\Delta_{1}$ et à $\Delta_{2}$ passant par $M$
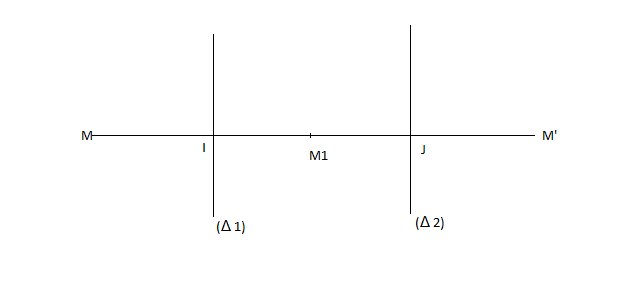
$S_{\Delta_{2}}\circ S_{\Delta_{1}}=t_{2\overrightarrow{IJ}}$
II.4 Rotation
II.4.1 Définition
Soient $\theta\in\mathbb{R}$ et $\Omega$ un point du plan. On appelle rotation d'angle $\theta$ et de centre $\Omega$ la transformation du plan notée $r_{(\Omega,\ \theta)}$ qui laisse $\Omega$ invariant et qui associe à tout point $M$ de $\mathcal{P}$ le point $M'$ tel que
$$\left\lbrace\begin{array}{lcl}\Omega M &=& \Omega M' \\\left(\overrightarrow{\Omega M},\ \overrightarrow{\Omega M'}\right) &=& \theta\ (2\pi)\end{array}\right.\;,\quad\theta \neq 0(2\pi)$$
$$\left\lbrace\begin{array}{lcl}\Omega M &=& \Omega M' \\\left(\overrightarrow{\Omega M},\ \overrightarrow{\Omega M'}\right) &=& \theta\ (2\pi)\end{array}\right.\;,\quad\theta \neq 0(2\pi)$$
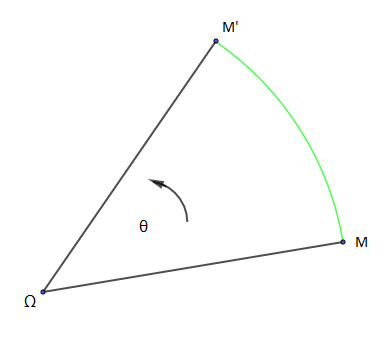
$\centerdot\ \ $ si $\theta=0(2\pi) \: \Longrightarrow \: r_{(\Omega,\ \theta)}=Id$
$\centerdot\ \ $ si $\theta=\pi(2\pi) \: \Longrightarrow \: r_{(\Omega,\ \theta)}=S_{\Omega}$
II.4.2 Points invariants
$\centerdot\ \ $ InV$r_{(\Omega,\ \theta)}=\{\Omega\}$. $\ \Omega$ est le seul point invariant.
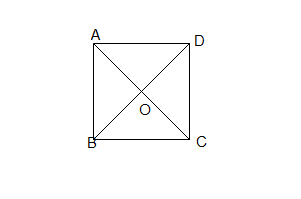
$\centerdot\ \ $ $ABCD$ carré direct alors $r_{(O,\ \frac{\pi}{2})}$ , $\ r_{(O,\ \pi)}$ et $r_{(O,\ -\frac{\pi}{2})}$ laissent globalement invariant le carré.
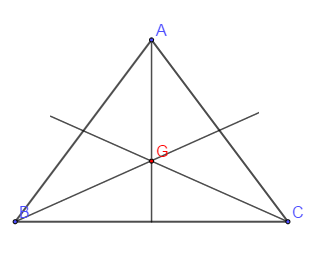
$\centerdot\ \ $ $ABC$ triangle alors $r_{(G,\ \frac{2\pi}{3})}$ et $r_{(G,\ -\frac{2\pi}{3})}$ laissent globalement invariant le triangle $ABC.$
II.4.3 Propriétés
$\centerdot\ \ $ $r_{(\Omega,\ \theta)}$ conserve le barycentre, les distances et les angles orientés. Donc, une rotation est un déplacement.
$\centerdot\ \ $ $r_{(\Omega,\ \theta)}$ conserve le parallélisme, la perpendiculaire et l'alignement.
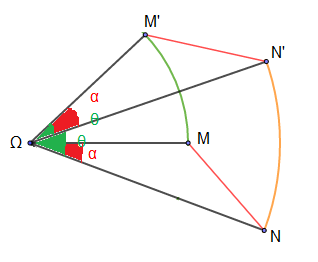
On a :
\begin{eqnarray} M'N'^{2}&=&\Omega M'^{2}+\Omega N'^{2}-2\Omega N'.\Omega M'.cos\alpha\nonumber \\ \\&=&\Omega M^{2}+\Omega N^{2}-2\Omega N.\Omega M.\cos\alpha\nonumber\\ \\ \text{Donc }\ M'N'^{2}&=&MN^{2}\nonumber\\ \\ \Rightarrow\ M'N'&=&MN\nonumber \end{eqnarray}
\begin{eqnarray} M'N'^{2}&=&\Omega M'^{2}+\Omega N'^{2}-2\Omega N'.\Omega M'.cos\alpha\nonumber \\ \\&=&\Omega M^{2}+\Omega N^{2}-2\Omega N.\Omega M.\cos\alpha\nonumber\\ \\ \text{Donc }\ M'N'^{2}&=&MN^{2}\nonumber\\ \\ \Rightarrow\ M'N'&=&MN\nonumber \end{eqnarray}
II.4.4 Expression complexe et analytique
Soient $\Omega\begin{pmatrix} a\\ b\end{pmatrix}$ d'affixe $z_{\Omega}=a+\mathrm{i}b=\alpha\ $, $\ M\begin{pmatrix} x\\ y\end{pmatrix}$ d'affixe $z_{M}=z=x+\mathrm{i}y$ et $M'\begin{pmatrix} x'\\ y'\end{pmatrix}$ d'affixe $z_{M'}=z'=x'+\mathrm{i}y'$.
On a :
$\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)=M'&\Leftrightarrow&\left\lbrace\begin{array}{rcl}\Omega M&=&\Omega M' \\ \left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}\right)&=&\theta (2\pi) \end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\dfrac{\Omega M'}{\Omega M}&=&1 \\ \\ \left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}\right)&=&\theta (2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\left|\dfrac{z'-z_{\Omega}}{z-z_{\Omega}}\right|&=&1 \\ \\ arg\;\left(\dfrac{z'-z_{\Omega}}{z-z_{\Omega}}\right)&=&\theta (2\pi)\end{array}\right.\end{array}$
Donc $\dfrac{z'-z_{\Omega}}{z-z_{\Omega}}=\mathrm{e}^{\mathrm{i}\theta} \: z'-z_{\Omega}=\mathrm{e}^{\mathrm{i}\theta}(z-z_{\Omega})$ ou $z'=\mathrm{e}^{\mathrm{i}\theta}z+\beta$
Ainsi, $z'=e^{\mathrm{i}\theta}z+\beta$ est l'expression complexe de la rotation d'angle $\theta$ et de centre $\Omega$ tels que $z_{\Omega}=\mathrm{e}^{\mathrm{i}\theta}z_{\Omega}+\beta$ , $z_{\Omega}=\dfrac{\beta}{1-\mathrm{e}^{\mathrm{i}\theta}}$
Autrement, soit $z'=\mathrm{e}^{\mathrm{i}\theta}z+\beta$ avec $\beta=\beta_{1}+\beta_{2}$
On a :
$\begin{array}{rcl} x'+\mathrm{i}y'&=&(\cos\theta+\mathrm{i}\sin\theta)(x+\mathrm{i}y)+\beta_{1}+\beta_{2}\\ \\ &\Rightarrow&\left\lbrace\begin{array}{rcl} x'&=&x\cos\theta-y\sin\theta+\beta_{1} \\ y'&=&y\cos\theta+x\sin\theta+\beta_{2} \end{array}\right.\end{array}$
qui est l'expression analytique
II.4.5 Composée et réciproque
On a :
$\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)=M'&\Leftrightarrow&\left\lbrace\begin{array}{rcl}\Omega M&=&\Omega M'\\ \left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M'}\right)&=&\theta (2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\Omega M'&=&\Omega M\\ \left(\overrightarrow{\Omega M'}\;,\ \overrightarrow{\Omega M}\right)&=&-\theta (2\pi)\end{array}\right.\\ \\ &\Leftrightarrow&M=r_{(\Omega\;,\ -\theta)}(M')=(r_{(\Omega\;,\ \theta)})^{-1}(M')\end{array}$
D'où, $(r_{(\Omega\;,\ \theta)})^{-1}=r_{(\Omega\;,\ -\theta)}$. La réciproque de la rotation de centre $\Omega$ et d'angle $\theta$ est la rotation de même centre $\Omega$ et d'angle $-\theta.$
$-\ $ même centre :
Soient $r_{1}$ et $r_{2}$ deux rotations de même centre $\Omega$ invariant.
On a :
$r_{1}=r_{(\Omega\;,\ \theta_{1})}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{1}}z+\alpha$
$r_{2}=r_{(\Omega\;,\ \theta_{2})}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta$
Soit $r=r_{1}\circ r_{2}$ la composée de $r_{1}$ et de $r_{2}$. On a :
$r=r_{1}\circ r_{2}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{1}}(\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta)+\alpha\ \Rightarrow\ z'=\mathrm{e}^{\mathrm{i}(\theta_{1}+\theta_{2})}z+\mathrm{e}^{\mathrm{i}\theta_{2}}\beta+\alpha$
$-\ $ si $\theta_{1}+\theta_{2}\neq 0(2\pi)$, alors $r_{1}\circ r_{2}$ est une rotation de centre $\Omega$ et d'angle $\theta=(\theta_{1}+\theta_{2}).$
$-\ $ si $\theta_{1}+\theta_{2}=0(2\pi)$, alors $\theta_{1}=-\theta_{2}$ et donc $r_{2}=r_{\left(\Omega\;,\ \theta_{1}\right)}=\left(r_{\left(\Omega\;,\ \theta_{2}\right)}\right)^{-1}.$
D'où, $r_{1}\circ r_{2}=Id$
$-\ $ centres différents :
$r_{1}$ et $r_{2}$ sont maintenant de centres différents. On a:
$r_{1}=r_{(\Omega_{1}\;,\ \theta_{1})}\ :\ z'-z_{\Omega_{1}}=\mathrm{e}^{\mathrm{i}\theta_{1}}(z-z_{\Omega_{1}})$ ou $z'=\mathrm{e}^{\mathrm{i}\theta_{1}}z+\alpha$
$r_{2}=r_{(\Omega_{2}\;,\ \theta_{2})}\ :\ z'-z_{\Omega_{2}}=\mathrm{e}^{\mathrm{i}\theta_{2}}(z-z_{\Omega_{2}})$ ou $z'=\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta$
Soit $r=r_{1}\circ r_{2}$ la composée de $r_{1}$ et de $r_{2}$. On a :
$r=r_{1}\circ r_{2}\ :\ z'=\mathrm{e}^{\mathrm{i}\theta_{1}}(\mathrm{e}^{\mathrm{i}\theta_{2}}z+\beta)+\alpha$
Donc, $M'$ est d'affixe $z'=\mathrm{e}^{\mathrm{i}(\theta_{1}+\theta_{2}}z+\delta$
$-\ $ si $\theta_{1}+\theta_{2}\neq 0(2\pi)\ \Rightarrow\ r_{1}\circ r_{2}$ est une rotation de centre $\Omega$ tel que $z_{\Omega}=\dfrac{\delta}{1-\mathrm{e}^{\mathrm{i}(\theta_{1}+\theta_{2})}}$ et d'angle $\theta=(\theta_{1}+\theta_{2}).$
$-\ $ si $\theta_{1}+\theta_{2}=0(2\pi)\ \Rightarrow\ r_{1}\circ r_{2}$ est une translation de vecteur $\vec{u}(\delta)$
$-\ $ composée d'une rotation $r_{(\Omega\;,\ \theta)}$ et d'une translation de vecteur $\vec{u}(\delta)$ :
Soient $r_{1}$ une rotation et $t$ une translation de vecteur, définies respectivement par : $r_{1}=r_{(\Omega\;,\ \theta)}$ ; $z'=\mathrm{e}^{\mathrm{i}\theta}z+\beta$ et $t_{\vec{u}}$ ; $z'=z+\alpha$
Considérons la composée $r=r_{1}\circ t$ définie par :
$r=r_{(\Omega\;,\ \theta)}\circ t_{\vec{u}}\;;\ z'=\mathrm{e}^{\mathrm{i}\theta}(z+\alpha)+\beta$ ou encore $z'=\mathrm{e}^{\mathrm{i}\theta}z+\delta$
$z'=\mathrm{e}^{\mathrm{i}\theta}z+\delta$ est l'expression complexe d'une rotation. Donc la composée d'une rotation et d'une translation est une rotation d'angle ; l'angle de la rotation et de centre ; le point invariant.
II.4.6 Décomposition d'une rotation
$\centerdot\ \ $ composée de deux symétries axiales d'axes sécants :
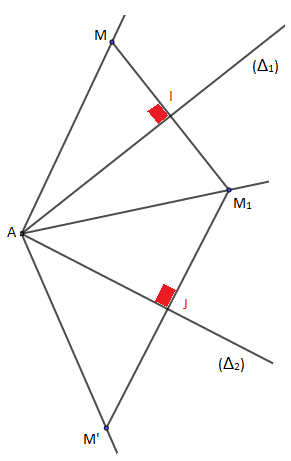
Soit $A$ le point d'intersection entre $\Delta_{1}$ et $\Delta_{2}$ ; on a :
$S_{\Delta_{2}}\circ S_{\Delta_{1}}(M)=S_{\Delta_{2}}(S_{\Delta_{1}}(M))=S_{\Delta_{2}}(M_{1})=M'$
De plus $AM=AM_{1}=AM'$
et
\begin{eqnarray}\left(\overrightarrow{AM}\;,\ \overrightarrow{AM'}\right)&=&\left(\overrightarrow{AM}\;,\ \overrightarrow{AM_{1}}\right)+\left(\overrightarrow{AM_{1}}\;,\ \overrightarrow{AM'}\right)\nonumber\\ \\ &=&2\left(\overrightarrow{AI}\;,\ \overrightarrow{AM_{1}}\right)+2\left(\overrightarrow{AM_{1}}\;,\ \overrightarrow{AJ}\right)\nonumber\\ \\ \Rightarrow\ \left(\overrightarrow{AM}\;,\ \overrightarrow{AM'}\right)&=&2\left(\overrightarrow{AI}\;,\ \overrightarrow{AJ}\right)\nonumber \end{eqnarray}
Donc $S_{\Delta_{2}}\circ S_{\Delta_{1}}(M)=M'\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} AM&=&AM'\\ \left(\overrightarrow{AM}\;,\ \overrightarrow{AM'}\right)&=&2\left(\overrightarrow{AI}\;,\ \overrightarrow{AJ}\right)(2\pi)\end{array}\right.$
Ce qui se traduit par : $M'=r_{[A\;,\ 2(\overrightarrow{AI}\;,\ \overrightarrow{AJ})]}(M)$
D'où, la composée $S_{\Delta_{2}}\circ S_{\Delta_{1}}$ de deux réflexions d'axes sécants en $A$ est une rotation de centre $A$ et d'angle $2\left(\widehat{\Delta_{1}\;,\ \Delta_{2}}\right)(2\pi)$
Toute rotation $r$ de centre $\Omega$ et d'angle $\theta$ peut se décomposer en une composée de symétries axiales d'axes $(\Delta_{1})$ et $(\Delta_{2})$ sécants en $\Omega$ ; le centre de la rotation est tel que $2\left(\widehat{\Delta_{1}\;,\ \Delta_{2}}\right)=\theta\;;\ (r=S_{\Delta_{2}}\circ S_{\Delta_{1}}).$
III Isométrie
III.1 Définition
Une isométrie du plan est une transformation qui conserve les distances, $\forall M$ et $N$ tels que $f(M)=M'$ et $f(N)=N'$ alors $M'N'=MN.$
III.2 Classification des isométries
$\centerdot\ \ $ une isométrie $f$ qui fixe trois points $A$ , $\ B$ et $C$ non alignés est l'identité.
$\centerdot\ \ $ une isométrie $f$ qui fixe deux points $A$ et $B$, si elle est différente de l'identité, est une symétrie axiale d'axe $(AB)$.
$\centerdot\ \ $ une isométrie $f$ qui a un seul point invariant $\Omega$ est une rotation de centre $\Omega$
Exercice d'application
Soit $f$ l'application définie par $$\left\lbrace\begin{array}{rcl} x'&=&\dfrac{1}{2}\left(x+y\sqrt{3}+1\right) \\ \\ y'&=&\dfrac{1}{2}\left(-x\sqrt{3}+y+\sqrt{3}\right)\end{array}\right.$$ qui, à tout $M\begin{pmatrix} x \\ y\end{pmatrix}$, associe le point $M'\begin{pmatrix} x' \\ y'\end{pmatrix}$
a) Montrer que $f$ est une isométrie
b) Déterminer InV$f$, en déduire que $f$ est une rotation dont on précisera le centre et l'angle.
Résolution
a) Soient $M_{1}\begin{pmatrix} x_{1} \\ y_{1}\end{pmatrix}$ et $M_{2}\begin{pmatrix} x_{2} \\ y_{2}\end{pmatrix}$ deux points du plan d'images respectives $M'_{1}\begin{pmatrix} x_{1}' \\ y_{1}'\end{pmatrix}$ et $M_{2}'\begin{pmatrix} x_{2}' \\ y_{2}'\end{pmatrix}$, alors
$\begin{array}{rcl} ||\overrightarrow{M_{1}'M_{2}'}||^{2}&=&(x_{2}'-x_{1}')^{2}+(y_{2}'-y_{1}')^{2}\\ \\ &=&\dfrac{1}{4}\left(x_{2}+y_{2}\sqrt{3}+1-x_{1}-y_{1}\sqrt{3}-1\right)^{2}+\\ \\ & &\dfrac{1}{4}\left(-x_{2}\sqrt{3}+y_{2}+\sqrt{3}+x_{1}\sqrt{3}-y_{1}-\sqrt{3}\right)^{2}\\ \\ &=&\dfrac{1}{4}\left((x_{2}-x_{1})+\sqrt{3}(y_{2}-y_{1})\right)^{2}+\dfrac{1}{4}\left(-\sqrt{3}(x_{2}-x_{1})+(y_{2}-y_{1})\right)^{2}\\ \\ &=&\dfrac{1}{4}\left((x_{2}-x_{1})^{2}+3(y_{2}-y_{1})^{2}+3(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}\right)\\ \\ &=&\dfrac{1}{4}\left(4(x_{2}-x_{1})^{2}+4(y_{2}-y_{1})^{2}\right)\\ \\ &=&(x_{2}-x_{1})^{2}+4(y_{2}-y_{1})^{2}\\ \\ &=&||\overrightarrow{M_{1}M_{2}}||^{2}\end{array}$
Donc, $||\overrightarrow{M_{1}'M_{2}'}||^{2}=||\overrightarrow{M_{1}M_{2}}||^{2}\ \Rightarrow\ M_{1}'M_{2}'=M_{1}M_{2}$, ce qui montre bien que $f$ est une isométrie.
b)
$\begin{array}{rcl} M\in\text{InV}f&\Leftrightarrow&f(M)=M\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x'&=&x \\ y'&=&y\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&\dfrac{1}{2}\left(x+y\sqrt{3}+1\right) \\ \\ y&=&\dfrac{1}{2}\left(-x\sqrt{3}+y+\sqrt{3}\right)\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl}\dfrac{1}{2}\left(-x+y\sqrt{3}+1\right)&=&0 \\ \\ \dfrac{1}{2}\left(-x\sqrt{3}-y+\sqrt{3}\right)&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} -x+y\sqrt{3}+1&=&0 \\ -x\sqrt{3}-y+\sqrt{3}&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&=&1 \\ y&=&0\end{array}\right.\end{array}$
Donc, InV$f=\Omega\begin{pmatrix} 1 \\ 0\end{pmatrix}$
$f$ est une isométrie qui a un seul point invariant $\Omega$, donc, $f$ est une rotation de centre $\Omega$ d'affixe 1.
Soit $z=x+\mathrm{i}y$ l'affixe de $M$ et $z'=x'+\mathrm{i}y'$ celui de $M'$, alors
$\begin{array}{rcl} z'&=&x'+\mathrm{i}y' \\ \\&=&\dfrac{1}{2}\left(x+y\sqrt{3}+1\right)+\dfrac{\mathrm{i}}{2}\left(-x\sqrt{3}+y+\sqrt{3}\right)\\ \\ &=&x\left(\dfrac{1}{2}-\dfrac{\mathrm{i}\sqrt{3}}{2}\right)+y\left(\dfrac{\sqrt{3}}{2}+\dfrac{\mathrm{i}}{2}\right)+\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}\\ \\ &=&(x+\mathrm{i}y)\left(\dfrac{1}{2}-\dfrac{\mathrm{i}\sqrt{3}}{2}\right)+\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}\\ \\ &=&\left(\dfrac{1}{2}-\dfrac{\mathrm{i}\sqrt{3}}{2}\right)z+\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}\end{array}$
Donc, $z'=\mathrm{e}^{-\mathrm{i}\tfrac{\pi}{3}}z+b$ avec $b=\dfrac{1}{2}+\dfrac{\mathrm{i}\sqrt{3}}{2}$. Ainsi, $f$ est une rotation de centre $\Omega$ et d'angle $\theta=-\dfrac{\pi}{3}.$
III.3 Propriétés
$\centerdot\ \ $ La réciproque d'une isométrie est une isométrie.
$\centerdot\ \ $ La composée d'une isométrie est une isométrie.
$\centerdot\ \ $ Une isométrie conserve le barycentre, le produit scalaire, l'alignement, le parallélisme, la perpendiculaire. L'image d'une figure quelconque est une figure de même nature et de même dimension.
$\centerdot\ \ $ Une isométrie qui conserve la mesure des angles orientés est appelée déplacement et celle qui change les signes des angles orientés est appelée antidéplacement.
III.4 Décomposition d'une isométrie
Soit $f$ une isométrie telle que $f(A)=A'$. Posons $t$ la translation de vecteur $\overrightarrow{A'A}$ ; $t=t_{\overrightarrow{A'A}}$ et $f_{1}=t\circ f$ est une isométrie.
Nous avons $f_{1}(A)=t\circ f(A)=t[f(A)]=t(A')=A$. Donc $f_{1}$ est une isométrie qui fixe $A$.
$f_{1}=t\circ f \: \Rightarrow \: t^{-1}\circ f_{1}=f$ où $t^{-1}=t_{\overrightarrow{AA'}}$.
Ainsi, toute isométrie $f$ peut se décomposer en une composition d'une translation et d'une isométrie qui fixe un point.
Théorème :
Etant donnés quatre points $A$, $\ B$, $\ C$ et $D$ tels que $AB=CD$, il existe une isométrie et une seule qui transforme $A$ en $C$ et $B$ en $D$.
Si $\overrightarrow{AB}=\overrightarrow{CD}$ alors l'isométrie est la translation de vecteur $\overrightarrow{AC}$.
Si $\overrightarrow{AB}\neq\overrightarrow{CD}$ alors l'isométrie est une rotation dont le centre est le point de rencontre des médiatrices de $[BC]$ et de $[BA]$ et d'angle $\theta=\left(\widehat{\overrightarrow{AB},\ \overrightarrow{CD}}\right)$ car
\begin{eqnarray} \left\lbrace\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)&=&M'\\ r_{(\Omega\;,\ \theta)}(N)&=&N' \end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} MN&=&M'N'\\ \left(\overrightarrow{MN}\;,\ \overrightarrow{M'N'}\right)&=&\theta (2\pi) \end{array} \right.\nonumber \end{eqnarray}
\begin{eqnarray} \left\lbrace\begin{array}{rcl} r_{(\Omega\;,\ \theta)}(M)&=&M'\\ r_{(\Omega\;,\ \theta)}(N)&=&N' \end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} MN&=&M'N'\\ \left(\overrightarrow{MN}\;,\ \overrightarrow{M'N'}\right)&=&\theta (2\pi) \end{array} \right.\nonumber \end{eqnarray}
Auteur:
Seyni Ndiaye & Diny Faye

Commentaires
Anonyme (non vérifié)
dim, 03/20/2022 - 15:45
Permalien
Bien fait.. mais est-ce que
Anonyme (non vérifié)
dim, 03/20/2022 - 15:46
Permalien
Bien fait
Kirikou (non vérifié)
dim, 07/21/2024 - 17:02
Permalien
suggestion
Ajouter un commentaire