Série d'exercices : Énergie potentielle - Énergie mécanique - 1er s
Classe:
Première
Exercice 1
Un chariot de montagne russe voyage du point $A$ jusqu'au point $D.$
Le chariot a une masse de $1000.0\,kg$ et une vitesse de $1.80\,m/s$ au point $A.$
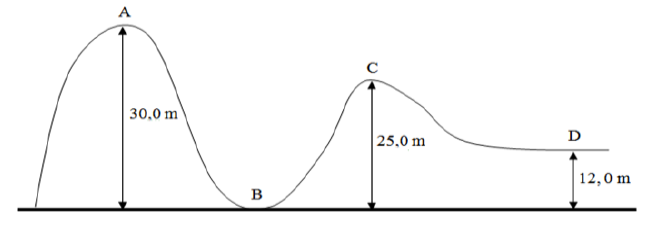
1) Quelle est l'énergie mécanique (énergie totale) du chariot au point $A$ ?
2) Quelle est la vitesse du chariot au point $B$ ?
3) Quelle est l'énergie potentielle et l'énergie cinétique du chariot au point $C$ ?
4) Quelle est la vitesse du chariot au point $D$ ?
Exercice 2
Paul, debout sur un pont, lance verticalement vers le haut une pierre de masse $m=70\,g.$
Celle-ci s'élève jusqu'à une hauteur de $10\,m$ au-dessus du point de lancement puis redescend et tombe dans l'eau.
La surface de l'eau est située $2.0\,m$ plus bas que le point de lancement de la pierre.
1. Calculer :
$-\ $ l'énergie potentielle de pesanteur de la pierre dans sa position la plus haute
$-\ $ l'énergie potentielle de pesanteur de la pierre dans sa position la plus basse
$-\ $ la variation d'énergie potentielle de la pierre
Si l'on choisit comme niveau de référence (origine de l'axe $Oz$ dirigé vers le haut)
1.1 Le niveau du point de lancement de la pierre
1.2 Le niveau de la surface de l'eau.
2. Exprimer l'énergie potentielle de pesanteur de la pierre lorsqu'elle est située à une altitude $z$ quelconque par rapport au point de lancement dans les deux cas précédents
Exercice 3
Un skieur à l'épreuve du kilomètre lancé $(KL)$, en recherche de vitesse sur une piste plane, bien damée et inclinée d'un angle $\alpha=26.0^{\circ}$ par rapport à l'horizontale, part du point $A$ et atteint une vitesse de $182\,km\cdot h^{-1}$ $(=50.5\,m\cdot s^{-1})$ au bout d'un $km$ de piste, au point $B.$
La masse du skieur et de son équipement est de $115\,kg.$
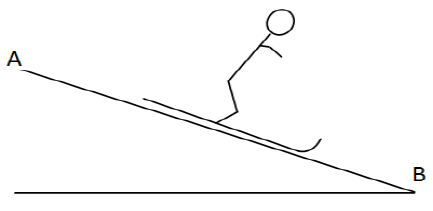
1) Donner l'expression littérale de l'énergie potentielle du skieur en $A.$
Faire l'application numérique correspondante en prenant comme origine des énergies potentielles le point $B.$
2) Donner l'expression littérale de l'énergie cinétique du skieur en $B.$
Faire l'application numérique correspondante.
3) Nommer les forces appliquées au système {skieur$+$équipement} et les représenter sur un schéma.
4) Donner l'expression du travail de chacune de ces forces.
5) Donner la relation liant la variation d'énergie cinétique du système et le travail des différentes forces.
6) Si le skieur glisse sans frottement.
Quelle serait alors sa vitesse au point $B$ ?
7) En fait les frottements ne sont pas négligeables lors d'une telle descente ; déterminer la valeur de ces frottements.
Exercice 4
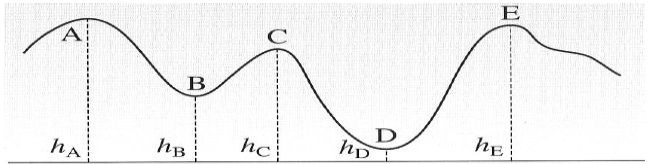
Dans un parc d'attractions, un wagonnet de masse $m=65\,kg$ se déplace sur des rails dont le profil est donné sur le schéma ci-dessous :
Les hauteurs des différents points $A$, $B$, $C$, $D$ et $E$ sont repérées par rapport au sol et ont pour valeurs :
$h_{A}=20\,m\quad h_{B}=10\,m\quad h_{C}=15\,m\quad h_{D}=5\,m\quad h_{E}=18\,m$
Calculer la variation d'énergie potentielle de pesanteur du wagonnet passant :
1) de $A$ à $B$
2) de $B$ à $C$
3) de $A$ à $D$
4) de $A$ à $E$
Exercice 5
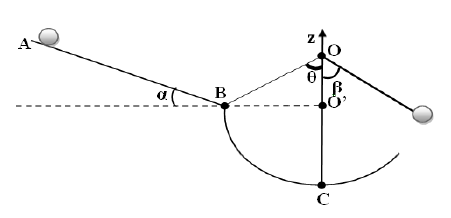
Une piste est constituée par un plan incliné $AB$ de longueur $l=2r$ d'un angle $\alpha=30^{\circ}$ sur l'horizontale et se raccordant tangentiellement à une portion $BC$ circulaire de centre $O$ et de rayon $r=OB=OC=50\,cm$
Un solide $(S)$ ponctuel de masse $m=50\,g$ est suspendu en $C$ au fil $OC$ accroché en $O.$ Un autre solide ponctuel $(S')$ de masse $m'=60\,g$ est lâché sans vitesse initiale au point $A$ et glisse sans frottement le long de la piste.
Au point $C$ il heurte de plein fouet le solide $(S).$
Prendre $g=9.8\,N\cdot Kg^{-1}$ et $\theta=60^{\circ}$
1. Le point $C$ étant considéré comme position de référence, exprimer l'énergie potentielle de pesanteur du solide $(S')$ au point $A$ en fonction de $m'$, $g$, $r$, $\alpha$ et $\theta$ et au point $B$ en fonction $m'$, $g$, $r$ et $\theta$
2.1 Calculer l'énergie mécanique totale du solide $(S')$ au point $A.$
2.2 Calculer la vitesse du solide $(S')$ au point $B$ et la vitesse qu'il a acquise juste avant le choc au point $C$ en supposant que les forces de frottement sont négligeables sur toute la piste
3. Le pendule constitué du solide $(S)$ et le fil s'écarte d'un angle $\beta$ par rapport à la position verticale d'équilibre stable du pendule avant le choc.
3.1 Exprimer l'énergie potentielle de pesanteur du solide $(S)$ en fonction de $m$, $g$, $r$ et $\beta$ ; la position verticale étant prise pour position de référence.
3.2 Calculer l'énergie mécanique du solide $(S)$ à son départ du point $C$ sachant qu'il acquiert une vitesse $v=3.4\,m\cdot s^{-1}$ juste après le choc.
3.3 Calculer le moment d'inertie $J$ du solide $(S)$ par rapport l'axe passant par le point $O'$ et l'écart maximal $\beta_{max}$ atteint par le solide $(S)$ en supposant négligeable la résistance de l'air.
Exercice 6
Un solide $(S)$ de masse $m=500\,g$ assimilable à un point matériel est lancé à partir d'un point $A$ sur un plan incliné d'un angle $\alpha_{0}=30^{\circ}$ par rapport à l'horizontal avec une vitesse $V_{A}=12\,m/s.$
La réaction d'intensité supposée constante exercée par le plan sur $(S)$ fait un angle $\alpha_{1}=30^{\circ}$ avec la normale au plan.
La composante de la réaction parallèle au plan incliné a un sens opposé au vecteur vitesse de $\overrightarrow{V}$ de $(S).$
1.1 Représenter les forces qui s'exercent sur $(S).$
1.2 Calculer les travaux de toutes ces forces au cours du déplacement $AB=\ell=1\,m.$
On donne $R=0.4\,N$ et $g=10\,N/kg.$
1.3 Déterminer la vitesse $V_{B}$ de $(S)$ au point $B.$
2. Calculer la variation de l'énergie mécanique de $(S)$ entre les points $A$ et $B.$
Dans ce qui suit, la résistance de l'air et les frottements sont supposés nuls.
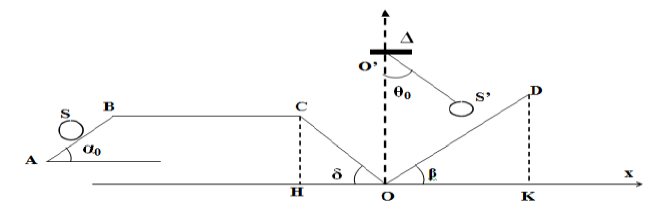
Le solide $(S)$ continue son mouvement sur $(BC)$ horizontal ; $(CO)$ incliné d'un angle $\delta=40^{\circ}$ par rapport à l'horizontal et $(OD)$ incliné d'un angle $\beta=30^{\circ}$ par rapport à l'horizontal.
En $O$, $(S)$ heurte un solide ponctuel $(S')$ de masse $m'=200\,g$ accroché à l'extrémité d'un fil de longueur $\ell'=10\,cm$ et de masse négligeable ; il s'écarte d'un angle $\theta_{0}$ par rapport à la verticale.
3. On prend comme position de référence le point $O$ d'altitude zéro.
3.1 Calculer les énergies potentielles de $(S)$ aux points $C$ et $D.$
$OH=OK=10\,cm.$
3.2 Lorsque le solide $(S)$ est sur la partie $(OD)$ de longueur $x\in[0\;;\ 0.1\,m]$, déterminer l'énergie potentielle de $(S)$ en un point de $[OD]$ en fonction de $x.$
3.3 Le solide $(S)$ rebrousse chemin en $D.$
Déterminer l'altitude maximale $Z_{max}$ atteinte sur $[OC]$ par $(S).$
4.1 Calculer le moment d'inertie de $(S')$ par rapport à l'axe $(\Delta).$
4.2 Exprimer l'énergie potentielle de $(S')$ en fonction de $m'$, $g$, $\ell$ et $\theta_{0}.$
4.3 Le solide $(S')$ part de sa position $\theta_{0}$, passe par sa position verticale puis remonte.
4.3.1 Déterminer sa vitesse angulaire au passage par sa position verticale avec $\theta_{0}=60^{\circ}.$
4.3.2 De quel angle $\theta_{max}$ remonte-t-il ?
5. On suppose que $(S)$ et $(S')$ ne se rencontrent plus.
Décrire qualitativement les mouvements ultérieurs de $(S)$ et $(S').$
Exercice 7
On néglige tous frottements.
Une bille de masse $m$ lancée du point $A$ à la vitesse $v_{A}$ se déplace sur un plan incliné vers le point $D.$
L'origine de l'énergie potentielle de pesanteur est le point le plus bas $A.$
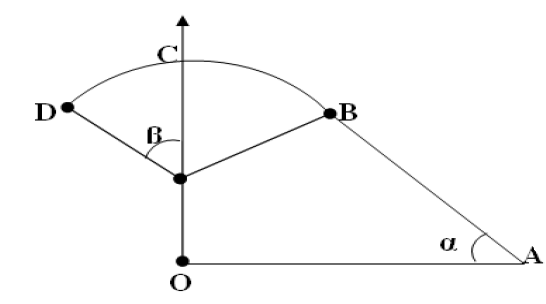
Données :
$m=1.0\,kg\ ;\ OB=0.50\,m\ ;\ AB=2.0\,m\ ;\ \alpha=20^{\circ}\ ;\ \beta=60^{\circ}\ ;\ v_{A}=18\,km/h\text{ et }g=9.8\,N/kg.$
1) Calculer les altitudes de $B$, $C$ et $D.$
2) Calculer l'énergie mécanique en $A.$
3) Calculer les vitesses en $C$ et en $D$ en $km/h.$
4) la vitesse initiale $v_{A}$ est divisée par deux, calculer :
5) L'énergie mécanique, les vitesses en $C$ et en $D.$
Exercice 8
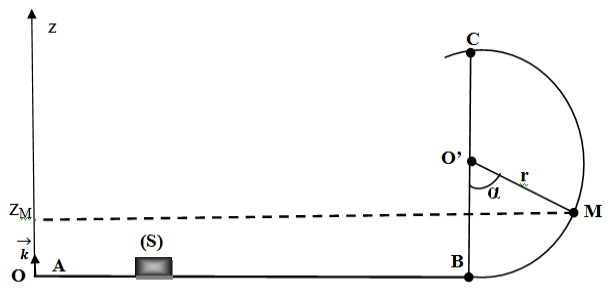
On considère le système mécanique représenté ci-dessous est formé par un parcours $ABC$ et un solide de masse $m=20.0\,g$, assimilable à un point matériel.
La partie $AB$ est rectiligne confondue avec le plan horizontal $(\Pi).$
La partie $BC$ est une boucle circulaire de rayon $r.$
On repère le solide dans cette boucle par l'abscisse angulaire $\theta=BOM$
Les frottements sont négligeables sur tout le parcours $ABC.$
On prend l'état de référence pour l'énergie potentielle de pesanteur le plan horizontal $(\Pi)$ et l'axe $Oz$ orienté vers le haut.
On donne $g=10\,N/kg$
1) Exprimer l'énergie potentielle de pesanteur du solide en en fonction de $m$, $g$, et $z$ l'altitude du solide mesurée à partir de l'état de référence choisi.
2) Déduire l'énergie potentielle de pesanteur au point $M$ en fonction de $m$, $g$, $r$, et $\alpha$
3) Pour quelle position l'énergie potentielle de pesanteur est maximale ?
Justifier votre réponse.
4) Trouver l'expression de l'énergie mécanique du solide aux points suivants : $A$, $B$ et $C$, sachant que le solide arrive au point $C$ avec une vitesse $v_{C}.$
5) Montrer que le solide parcours le périmètre du boucle, on doit avoir $EC(A)>2mgr.$
6) On donne $r=1.5\,m$, calculer la valeur de la vitesse initiale $v_{A}$ pour que le solide arrête au point $C$
Exercice 9
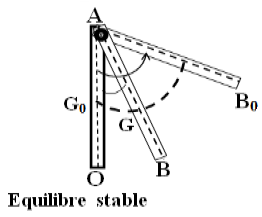
Une barre $AB$ homogène de longueur $L=1\,m$, est mobile autour d'un axe horizontal passant par le point $A$ de son extrémité.
Son moment d'inertie par rapport à cet axe est $J\Delta=1/3\,m\cdot L^{2}.$
On écarte la barre de sa position d'équilibre stable d'un angle $\alpha=60^{\circ}$ et on le lance, à l'instant $t=0$ avec une
vitesse angulaire $w_{0}=2\,rad/s$
Les frottements sont négligeables.
On prend l'état de référence pour l'énergie potentielle de pesanteur le plan horizontal qui passe par $O'$ et l'axe $Oz$ orienté vers le haut.
On donne $g=10\,N/kg$
1) Calculer la vitesse linéaire $v_{B}$ du point $B$ à l'instant $t=0$
2) Trouver l'expression de la variation de l'énergie cinétique entre la position initiale et la position de la barre d'abscisse angulaire $\theta=OAB$ en fonction de $L$, $m$, $g$, $\theta_{0}$ et $\theta$
3) Montrer que l'expression de la vitesse angulaire $w$ lorsque la barre passe par la position d'abscisse angulaire $\theta$ est donnée par la relation suivante :
$$w=\sqrt{w_{0}^{2}+\dfrac{3g\left(\cos\theta-\cos\theta_{0}\right)}{L}}$$
4) Calculer la vitesse linéaire $v_{B}$ lorsque la barre passe par sa position d'équilibre stable
Exercice 10
Un solide de masse $m_{1}=100\,g$ peut coulisser le long d'un plan inclinée $\alpha=30^{\circ}$ par à rapport à l'horizontal
Le solide $S$ est relié à un ressort de constante de raideur $100\,N/m$ dont l'autre extrémité est fixe (voir figure)
La position $O$, à l'équilibre, de l'extrémité $M$ du ressort est prise comme origine $(O\;,\ \vec{i})$ d'un repère orienté comme le montre la figure
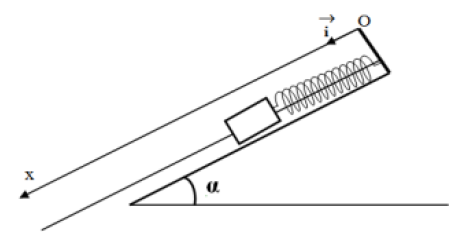
1) Donner l'expression littérale et calculer potentielle élastique $E_{pe}$ du système en équilibre en fonction de l'allongement $\Delta Δ_{l0}$ du ressort.
Donnée : $g=10\,N/kg$
2) Un manipulateur saisit le solide $S$ et le tire vers de telle sorte que l'abscisse de $M$ soit égale $X_{M}=-a=-3\,cm$
Donner l'expression littérale et calculer l'énergie potentielle élastique du système
3) Donner l'expression littérale et calculer l'énergie potentielle de pesanteur du solide en adoptant la position d'équilibre initiale comme état de référence
4) Le manipulateur lâche le solide $S$ qui effectue alors des oscillations le long du plan incliné d'amplitude $a$ ; les frottements sont négligeables
Donner l'expression en fonction de $x$ de l'énergie-potentielle élastique $E_{pe}$ et de l'énergie potentielle de pesanteur
En déduire l'expression de l'énergie cinétique $E_{C}$
Calculer la vitesse du solide lorsque $x=2\,cm$
5) Représenter graphiquement en fonction de $x$, $E_{PP}$, $E_{Pe}$ et $E_{C}$
Mettre en évidence l'expression de la somme $E_{M}=E_{PP}+E_{Pe}+E_{C}$
Exercice 11 Énergie
Un solide de masse $m=200\,g$ se déplace dans une glissière constituée d'une partie rectiligne $BC$ et d'une partie circulaire $BD$ de centre $O$ et de rayon.
On néglige des frottements.
$G=10\,N/kg.$
L'origine des altitudes est le point $B$ et celle des énergies potentielles est le plan horizontal contenant $B$ (voir figure 1)
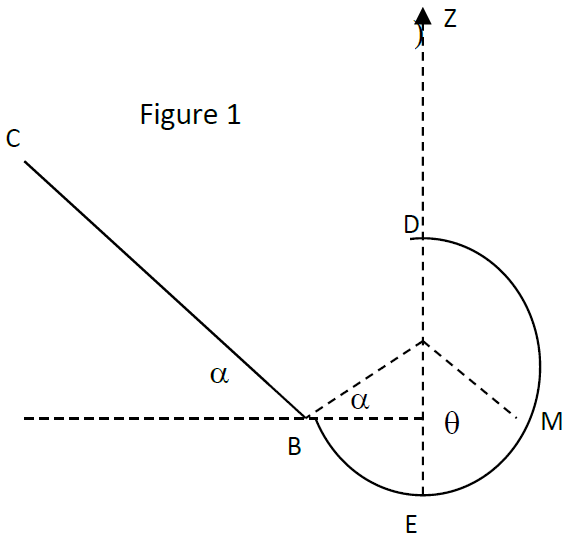
Le solide part du point $C$ avec une vitesse initiale de $1.6\,m/s$
1) Représenter en $C$ et en $M$ les forces appliquées au solide
2) Calculer les altitudes $Z_{c}$ et $Z_{e}$ des points $C$ et $E$ ; en déduire l'énergie potentielle du solide lorsqu'il se trouve en chacun de ces points.
On donne $CB=5\,m\ ;\ \alpha=20^{\circ}\ ;\ R=1\,m$
3) Calculer le travail du poids lorsque le solide passe de $C$ à $B.$
En déduire l'énergie cinétique du solide au point $B$
4) Calculer l'énergie mécanique du solide en $B$
5) Donner l'expression de la vitesse $V_{M}$ du solide du point $M$ en fonction de $V_{E}$, $m$, $g$, $r$ et $\theta$
AN :
calculer $V_{m}$ pour $\theta=\dfrac{\pi}{2}$
6) Le solide pourra-t-il atteindre le point $D$ ?

Commentaires
Anonyme (non vérifié)
mar, 01/14/2020 - 21:58
Permalien
Pdf
ISSAKA (non vérifié)
lun, 04/27/2020 - 10:46
Permalien
Corrigé de tous les exercices
Zineb elghazouani (non vérifié)
dim, 01/31/2021 - 17:06
Permalien
Correctoin les exercices
Manoutchoo (non vérifié)
ven, 01/27/2023 - 08:18
Permalien
Apprendre
Karim (non vérifié)
sam, 01/22/2022 - 21:55
Permalien
Phisique
Kouadio yao (non vérifié)
sam, 12/16/2023 - 22:15
Permalien
J'ai un partiel à faire aider
zakaria konate (non vérifié)
dim, 04/17/2022 - 12:52
Permalien
correction
Fatou Diédhiou (non vérifié)
dim, 11/13/2022 - 19:25
Permalien
Il manque la correction
Ammar (non vérifié)
mar, 01/17/2023 - 19:35
Permalien
Être bon en physique et chimie
Medune (non vérifié)
mar, 12/26/2023 - 12:22
Permalien
Correction
Malki sara (non vérifié)
dim, 02/09/2025 - 20:23
Permalien
Physique
Khoyane (non vérifié)
ven, 03/26/2021 - 17:20
Permalien
Téléphone
Elemin (non vérifié)
lun, 06/07/2021 - 00:16
Permalien
Physical
Ismaël (non vérifié)
mar, 03/21/2023 - 02:17
Permalien
Apprendre
Anonyme (non vérifié)
ven, 11/17/2023 - 14:29
Permalien
Pdf
Anonyme (non vérifié)
ven, 11/17/2023 - 14:29
Permalien
Pdf
اسماعيل (non vérifié)
sam, 03/02/2024 - 09:53
Permalien
لتصحیح اخطائي
Yyy (non vérifié)
dim, 03/24/2024 - 11:30
Permalien
Pc
Anonyme (non vérifié)
jeu, 01/16/2025 - 16:06
Permalien
Nice
El voulany (non vérifié)
mar, 02/10/2026 - 20:47
Permalien
Demande de pdf
Sanou Mahamoud (non vérifié)
jeu, 02/20/2020 - 10:29
Permalien
Exercice corrigé de physique chimie
Ouoba Mohamed b... (non vérifié)
ven, 03/06/2020 - 00:28
Permalien
C'est très intéressant pour
ahmed (non vérifié)
mer, 12/09/2020 - 11:06
Permalien
tres bon travail
LM (non vérifié)
mar, 03/31/2020 - 04:37
Permalien
correction de ces exercices
Anonyme (non vérifié)
sam, 09/05/2020 - 16:08
Permalien
Désolé mais pour le 1e
Bere (non vérifié)
sam, 01/23/2021 - 20:29
Permalien
Physique
zaki (non vérifié)
sam, 01/08/2022 - 22:41
Permalien
hhh
zaki (non vérifié)
sam, 01/08/2022 - 22:45
Permalien
hhh
Anonyme (non vérifié)
lun, 04/05/2021 - 17:02
Permalien
C vrai même moi aussi bref
Soum (non vérifié)
lun, 01/11/2021 - 00:48
Permalien
Correction de l exo 8
Ezéchiel (non vérifié)
mar, 02/09/2021 - 14:06
Permalien
Correction des exercices
Seye (non vérifié)
mer, 03/24/2021 - 19:12
Permalien
Élève en classe première s2
Anonyme (non vérifié)
ven, 03/26/2021 - 17:17
Permalien
Bien
Elie (non vérifié)
ven, 03/26/2021 - 17:17
Permalien
Pc
Khoyane (non vérifié)
ven, 03/26/2021 - 17:19
Permalien
Trop bien
Anonyme (non vérifié)
lun, 04/05/2021 - 17:04
Permalien
La correction exo 1 qust 4
zaynab zaynab (non vérifié)
dim, 12/12/2021 - 17:09
Permalien
j'ai admiré ces exercices,
bahb6015@gmail.com (non vérifié)
mer, 12/22/2021 - 20:59
Permalien
Ils très bon
Iman (non vérifié)
sam, 01/22/2022 - 17:07
Permalien
Exercice 5
Esaïe (non vérifié)
dim, 04/24/2022 - 15:28
Permalien
Je veux savoir
Seedorf baddest (non vérifié)
ven, 12/22/2023 - 21:22
Permalien
Le résultat
yassin (non vérifié)
mer, 01/04/2023 - 21:57
Permalien
pdf
Keita Mohamed sama (non vérifié)
dim, 01/08/2023 - 22:13
Permalien
Apprendre
Nestor (non vérifié)
dim, 01/08/2023 - 23:02
Permalien
Étude
Anonyme (non vérifié)
mar, 01/10/2023 - 23:12
Permalien
Merci
Dezoumbe Elie (non vérifié)
ven, 03/22/2024 - 09:36
Permalien
Apprendre
KPANTE (non vérifié)
ven, 01/17/2025 - 17:27
Permalien
VOIR CORRIGe
Ajouter un commentaire