Dérivabilité - T S

Classe: 
Terminale
 

I. Nombre dérivé

I.1. Définitions

$-\ \ $ On dit qu'une fonction $f$ est dérivable en $x_{0}\in D_{f}$ si, et seulement si, l'une des conditions équivalentes suivantes est vérifiée.
 
$\centerdot\ \ C_{1}\ :\ \lim\limits_{x\rightarrow x_{0}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=\ell\in\mathbb{R}$ (réel fini)
 
$\centerdot\ \ C_{2}\ :\ \lim\limits_{h\rightarrow 0}\dfrac{f(x_{0}+h)-f(x_{0})}{h}=\ell\in\mathbb{R}$
 
$\centerdot\ \ C_{3}\ :\ $ il existe un réel $\ell$ et une fonction $\varepsilon$ tels que f(x0+h)=f(x0)+ℓh+hε(h)avec limh→0ε(h)=0
Dans ce dernier cas on dit que $f$ admet un développement limité d'ordre 1 au voisinage de $x_{0}.$
 
$\ell$ est le nombre dérivé de $f$ en $x_{0}$ noté $f'(x_{0}).$
f′(x0)=ℓ
$-\ \ $ On dit qu'une fonction $f$ est dérivable à gauche de $x_{0}\in D_{f}$ si, et seulement si, 
limx→x0−f(x)−f(x0)x−x0=ℓ1∈R(réel fini)
$\ell_{1}$ est le nombre dérivé de $f$ à gauche de $x_{0}$ noté $f'_{g}(x_{0}).$
fg′(x0)=ℓ1
$-\ \ $ On dit qu'une fonction $f$ est dérivable à droite de $x_{0}\in D_{f}$ si, et seulement si,
limx→x0+f(x)−f(x0)x−x0=ℓ2∈R(réel fini)
$\ell_{2}$ est le nombre dérivé de $f$ à droite de $x_{0}$ noté $f'_{d}(x_{0}).$
fd′(x0)=ℓ2

Théorème 1

Une fonction $f$ est dérivable en $x_{0}$ si, et seulement si, $f$ est dérivable à gauche et à droite de $x_{0}$ et que les nombres dérivés sont égaux $(f'_{g}(x_{0})=f'_{d}(x_{0}))$

Exercice d'application

Soit $f$ et $g$ deux fonctions définies par : f(x)=|x2−x|etg(x)=x2−4x+3
Étudier la dérivabilité de $f$ et $g$ en 1.

Résolution

Dérivabilité de $f$ en 1
 
Écrivons $f$ sans le symbole des valeurs absolues en utilisant le tableau de signe suivant :
x−∞01+∞x2−x+0−0+|x2−x|x2−x|−x2+x|x2−x
 
Donc, 
 
$limx→1−f(x)−f(1)x−1=limx→1−−x2+xx−1=limx→1−(−x)=−1$
 
$limx→1+f(x)−f(1)x−1=limx→1+x2−xx−1=limx→1+(x)=1$
 
Ainsi, $f'_{g}(1)\neq f'_{d}(1)$
 
D'où, $f$ n'est pas dérivable en 1.
 
Dérivabilité de $g$ en 1
 
D'après le tableau de signes ci-dessous on a $D_{g}=]-\infty\;;\ 1]\cup[3\;;\ +\infty[$
 
x−∞13+∞x2−4x+3+0−0+
 
Alors,
 
$limx→1−g(x)−g(1)x−1=limx→1−x2−4x+3x−1=limx→1−(x−1)(x−3)(x−1)x2−4x+3=−∞$
 
Donc, $g$ non dérivable en $1.$

I.2. Interprétation géométrique de la dérivabilité

Nous distinguons deux cas :
 
$\centerdot\ \ $ Soit $f$ dérivable en $x_{0}$ alors $\lim\limits_{x\rightarrow x_{0}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=f'(x_{0})\in\mathbb{R}$
 
On a : $\lim\limits_{h\rightarrow 0}\dfrac{f(x_{0}+h)-f(x_{0})}{h}$ est le coefficient directeur de la sécante $(AB).$

 

 
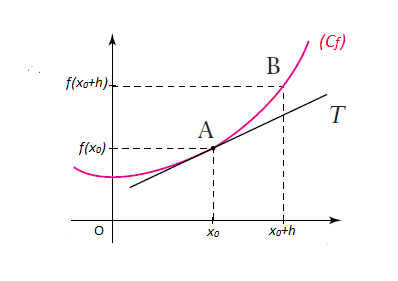
Alors, lorsque $h$ tend vers $0$ le point $B$ tend vers le point $A.$
 
Et par conséquent, la droite $(AB)$ tend vers une droite dite limite $(T)$ appelée tangente à $C_{f}$ en $x_{0}.$
 
Ainsi, au point d'abscisse $x_{0}$ on a une tangente $(T)$ d'équation : y=f′(x0)(x−x0)+f(x0)
$f'(x_{0})$ est le coefficient directeur de la tangente.
 
$\centerdot\ \ $ Soit $f$ non dérivable en $x_{0}$ ; les cas suivants peuvent alors se présenter :
 
$-\ \ $ deux demi-tangentes au point d'abscisse $x_{0}.$ 
 
Par exemple $f'_{g}(x_{0})=-2\ $ et  $\ f'_{d}(x_{0})=\dfrac{2}{3}$

 

 
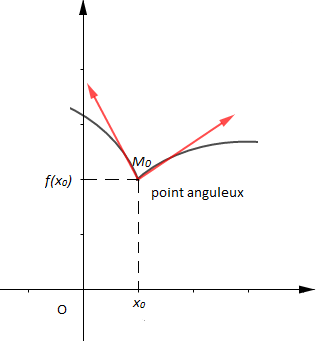
Les équations des demi-tangentes sont données par :
 
$T_{1}\ :\ y=f'_{g}(x_{0})(x-x_{0})+f(x_{0})$ avec $f'_{g}(x_{0})=-2$
 
$T_{2}\ :\ y=f'_{d}(x_{0})(x-x_{0})+f(x_{0})$ avec $f'_{d}(x_{0})=\dfrac{2}{3}$
 
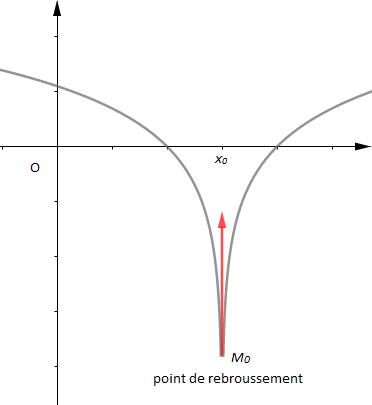
$-\ \ $ une demi-tangente verticale au point d'abscisse $x_{0}.$
 
Par exemple : 
 
$\lim\limits_{x\rightarrow x_{0}^{-}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=-\infty\ $ et $\ \lim\limits_{x\rightarrow x_{0}^{+}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=+\infty$

 

 
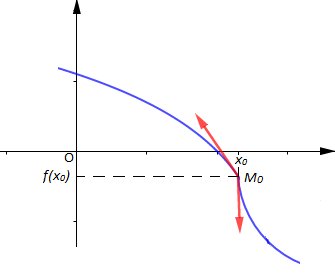
$-\ \ $ une demi-tangente de pente fini et une demi-tangente verticale au point d'abscisse $x_{0}.$
 
Par exemple :
 
$f'_{g}(x_{0})=-2\ $ et $\ \lim\limits_{x\rightarrow x_{0}^{+}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=+\infty$

 

 

I.3. Opérations sur la dérivabilité

Théorème 2

Si une fonction $f$ est dérivable en $x_{0}$ alors $f$ est continue en $x_{0}$ ; la réciproque est fausse.
 
Par exemple la fonction $f(x)=|x^{2}-x|$ qui est continue en $1$ et non dérivable en $1.$
 
Preuve théorème
 
$f$ dérivable en $x_{0}$ alors il existe une fonction $\varepsilon$ telle que f(x0+h)=f(x0)+hf′(x0)+hε(h)avec limh→0ε(h)=0
Posons $x=x_{0}+h$ donc, $f(x)=f(x_{0})+(x-x_{0})f'(x_{0})+(x-x_{0})\varepsilon(x-x_{0})$
 
Ainsi, 
 
$limx→x0f(x)=limx→x0f(x0)+(x−x0)f′(x0)+(x−x0)ε(x−x0)=f(x0)$
 
D'où, $f$ continue en $x_{0}$

Théorème 3

Si $f$ et $g$ sont deux fonctions dérivables en $x_{0}$ alors :
 
$\centerdot\ \ f+g$ est dérivables en $x_{0}$ et (f+g)′(x0)=f′(x0)+g′(x0)
$\centerdot\ \ fg$ est dérivables en $x_{0}$ et (fg)′(x0)=f′(x0)g(x0)+f(x0)g′(x0)
$\centerdot\ \ $ si de plus $g(x)\neq 0$ alors $\dfrac{f}{g}$ est dérivables en $x_{0}$ et (fg)′(x0)=f′(x0)g(x0)−f(x0)g′(x0)(g(x0))2

Théorème 4 (composée)

Si une fonction $f$ est dérivable en $x_{0}\ $ et $\ g$ dérivable en $y_{0}=f(x_{0}$ alors $g\circ f$ est dérivable en $x_{0}$ et (g∘f)′(x0)=f′(x0)×g′[f(x0)]

II. Fonctions dérivées

II.1. Définition

On appelle fonction dérivée de $f$ la fonction notée $f'$ qui associe à tout $x$ son nombre dérivé.

II.2. Tableau de dérivées

ff′ff′ff′ff′k∈R0sin⁡xcos⁡x1u−u′u2tan⁡uu′cos2⁡uaxacos⁡x−sin⁡xuu′2uunnu′un−11x−1x2tan⁡x1cos2⁡xsin⁡uu′cos⁡uuvu′v−uv′v2x12xxnnxn−1cos⁡u−u′sin⁡uuvu′v+uv′
 
$u$ une fonction dérivable

Exercice d'application 

Calculer les dérivées des fonctions $f\ $ et $\ g$ définies par : 
 
$f(x)=(x-1)\sqrt{x^{2}-4x+3}\;,\ g(x)=\sin^{4}(4x^{2}-3x+5)$

Résolution

Soit $f(x)=(x-1)\sqrt{x^{2}-4x+3}\ $ alors sa dérivée $f'(x)$ est donnée par : 
 
$f′(x)=x2−4x+3+(x−1)×2x−42x2−4x+3=x2−4x+3+(x−1)(x−2)x2−4x+3=x2−4x+3+x2−3x+2x2−4x+3$
 
D'où, $f'(x)=\dfrac{2x^{2}-7x+5}{\sqrt{x^{2}-4x+3}}$
 
On a $g(x)=\sin^{4}(4x^{2}-3x+5)$
 
alors, $g'(x)=4(8x-3)\cos(4x^{2}-3x+5)\sin^{3}(4x^{2}-3x+5)$

II.3. Dérivées successives

$\centerdot\ \ $ Si $f$ est dérivable sur $I$ et si sa fonction dérivée $f'$ est dérivable sur $I$ on dira que $f$ est deux fois dérivable sur $I$ et la dérivée seconde est notée $f''(x)$
 
$\centerdot\ \ $ Si $f''$ est dérivable sur $I$ on dira que $f$ est trois fois dérivable sur $I$ et la dérivée troisième est notée $f^{(3)}(x)$
 
$\centerdot\ \ $ Si $f$ est $n$ fois dérivable sur $I$ sa dérivée $n^{\text{ième}}$ est notée $f^{(n)}(x)$
 
Par exemple, la dérivée $n^{\text{ième}}$ des fonctions $f(x)=\sin x$ et $g(x)=\cos x$ est donnée par : f(n)(x)=sin⁡(x+nπ2),g(n)(x)=cos⁡(x+nπ2)
$\centerdot\ \ $ Si $f$ et $g$ sont $n$ fois dérivable sur $I$ alors, (fg)(n)=∑k=0nCnkf(k)(x)g(n−k)(x)

III. Applications

III.1. Sens de variation

$\centerdot\ \ $ Si $f'(x)\geq 0$ sur $I$ alors, $f$  est croissante sur $I.$
 
$\centerdot\ \ $ Si $f'(x)\leq 0$ sur $I$ alors,  sur $I$, alors  $f$ est décroissante sur $I.$
 
$\centerdot\ \ $ Si $f'(x)=0$ sur $I$ alors, la fonction  $f$ est constante sur $I.$
 
$\centerdot\ \ $ Si $f'(x)>0$ sur $I$ alors, $f$ est strictement croissante sur $I.$
 
$\centerdot\ \ $ Si $f'(x)<0$ sur $I$ alors,  sur $I$, alors  $f$ est strictement décroissante sur $I.$

Exercice d'application

Soit $f$ la fonction définie par : $f(x)=|x^{2}-x|$
 
1) Déterminer les limites aux bornes de $D_{f}$
 
2) Étudier la dérivabilité en 0 et 1
 
3) Donner la dérivée et dresser le tableau de variation

Résolution

1) Soit $f(x)=|x^{2}-x|$ alors, $D_{f}=\mathbb{R}$ et en écrivant $f$ sans le symbole des valeurs absolues on obtient :
f(x)={x2−xsix∈]−∞; 0]∪[1; +∞[−x2+xsix∈]0; 1[
Ainsi, 
 
$limx→−∞f(x)=limx→−∞x2−x=+∞$
 
$limx→+∞f(x)=limx→+∞x2−x=+∞$
 
2) Dérivabilité de $f$ en $0$
 
On a 
 
$limx→0−f(x)−f(0)x−0=limx→0−x2−xx=limx→0−(x−1)=−1$
 
$limx→0+f(x)−f(0)x−0=limx→0+−x2+xx=limx→0+(−x+1)=1$
 
Ainsi, $f'_{g}(0)\neq f'_{d}(0)$
 
D'où, $f$ n'est pas dérivable en $0.$
 
Dérivabilité de $f$ en $1$
 
On a 
 
$limx→1−f(x)−f(1)x−1=limx→1−−x2+xx−1=limx→1−(−x)=−1$
 
$limx→1+f(x)−f(1)x−1=limx→1+x2−xx−1=limx→1+(x)=1$
 
Ainsi, $f'_{g}(1)\neq f'_{d}(1)$
 
D'où, $f$ n'est pas dérivable en $1.$
 
3) Soit $f'(x)$ la fonction dérivée de $f$ alors on a : f(x)={2x−1six∈]−∞; 0[∪]1; +∞[−2x+1six∈]0; 1[
Tableau de variation de $f$
x−∞01/21+∞f′(x)−−1||1+0−−1||1+−∞1/4+∞f↘↗↘↗00

III.2. Extrémums - point d'inflexion

$\centerdot\ \ $ On dit qu'une fonction $f$ présente un extrémum au point d'abscisse $x_{0}$ si $f'(x)$ s'annule en $x_{0}$ en changeant de signe autour de $x_{0}.$
xx0f′(x)−0+|f↘|↗minimum
On peut aussi formuler ainsi : 
 
Il existe $\alpha>0$ tel que $\forall\;x\in\;]x_{0}-\alpha\;;\ x_{0}+\alpha[\;,\quad f(x)\geq f(x_{0})$
xx0f′(x)+0−maximumf↗|↘|
On peut alors formuler ainsi : 
 
Il existe $\alpha>0$ tel que $\forall\;x\in\;]x_{0}-\alpha\;;\ x_{0}+\alpha[\;,\quad f(x)\leq f(x_{0})$
 
$\centerdot\ \ $ On dit que $M_{0}(x0y0)$ est une point d'inflexion si :
 
$\ast\ \ f'(x)$ garde un signe constant autour de $x_{0}$
 
$\ast\ \ f''(x)$ s'annule en $x_{0}$ en changeant de signe.
 
Par exemple
xx0f″(x)+0−f′(x)+|+ouxx0f″(x)+0−f′(x)−|−
ou encore
xx0f″(x)−0+f′(x)+|+ouxx0f″(x)−0+f′(x)−|−
Remarque : un point d'inflexion est un point où la courbe traverse sa tangente.

III.3. Dérivée de la réciproque d'une fonction

III.3.1. Théorème 5 : bijection

Si $f$ est une fonction continue et strictement monotone sur $I$ alors $f$ est une bijection de $I$ vers $J=f(I)$ et donc $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement monotone dans le même sens que $f$ de $J$ vers $I$ et $f^{-1}$ est dérivable sur $J_{1}=J\setminus\{y\in J\;/\;f'(f^{-1}(y))=0\}$ et on a : ∀y0∈J1; (f−1)′(y0)=1f′(x0)
où $f(x_{0})=y_{0}\;;\ x_{0}\in I.$
 
Remarque : pour obtenir $x_{0}$ on résout l'équation $f(x)=y_{0}$

Exercice d'application

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x^{3}-3x+1$
 
1) Montrer que $f$ admet une bijection réciproque sur $[1\;;\ +\infty[$
 
2) Calculer $(f^{-1})'(1)$

Résolution

1) Soit $f(x)=x^{3}-3x+1$ alors, $f'(x)=3x^{2}-3=3(x-1)(x+1)$
 
Donc, $f'(x)$ positive sur $]-\infty\;;\ -1[\cup]1\;;\ +\infty[$ et négative sur $]-1\;;\ 1[.$
 
$limx→−∞f(x)=limx→−∞x3−3x+1=−∞$
 
$limx→+∞f(x)=limx→+∞x3−3x+1=+∞$
 
Tableau de variation de $f$
x−∞−11+∞f′(x)+0−0+3+∞f↗↘↗−∞−1
Ainsi, $f$ est continue et strictement croissante sur $[1\;;\ +\infty[$ donc bijective de $[1\;;\ +\infty[$ vers $[-1\;;\ +\infty[.$
 
Par suite $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement croissante de $[-1\;;\ +\infty[$ vers $[1\;;\ +\infty[$ et $f^{-1}$ est dérivable sur $]-1\;;\ +\infty[.$ 
 
2) Calculons $(f^{-1})'(1)$
 
On a : $(f^{-1})'(1)=\dfrac{1}{f'(x_{0})}$ avec $f^{-1}(1)=x_{0}$ ; c'est-à-dire $f(x_{0})=1.$
 
Donc, résolvons l'équation $f(x)=1.$ On a :
 
$f(x)=1⇔x3−3x+1=1⇔x3−3x=0⇔x=0oux=−3oux=3$
 
Or, $\sqrt{3}$ est l'unique solution qui appartient à $[1\;;\ +\infty[$ donc, $x_{0}=\sqrt{3}.$
 
Par suite,
 
$(f−1)′(1)=1f′(x0)=1f′(3)=13×3−3=16$
 
D'où, $(f^{-1})'(1)=\dfrac{1}{6}$

III.3.2. Dérivée des fonctions réciproques de : $\sin x\;;\ \cos x\;;\ \tan x$

$\centerdot\ \ $ Soit $f(x)=\sin x\ $ alors, $D_{f}=\mathbb{R}$ et $T=2\pi.$ 
 
$f$ impaire donc le domaine d'étude est donné par $D_{E}=[0\;;\ \pi].$
 
Soit $f'(x)=\cos x$ alors le tableau de variation de $f$ est :
x0π/2πf′(x)+0−1f↗↘00
Ainsi, $f$ est continue et strictement croissante sur $\left[0\;;\ \dfrac{\pi}{2}\right]$ donc $f$ est une bijection de $\left[0\;;\ \dfrac{\pi}{2}\right]$ vers $[0\;;\ 1].$
 
D'où, $f$ admet une bijection réciproque $f^{-1}$, notée $\arcsin$, qui est continue et strictement croissante de $[0\;;\ 1]$ vers $\left[0\;;\ \dfrac{\pi}{2}\right]$ et $\arcsin$ est dérivable sur $[0\;;\ 1[$ et on a : (f−1)′(y)=1f′(x)=1cos⁡x
Or, 
 
$cos2⁡x+sin2⁡x=1⇒cos⁡x=±1−sin2⁡x=+1−sin2⁡xcar  x∈[0; π2]⇒cos⁡x=1−y2$
 
Ce qui entraîne alors, $(f^{-1})'(y)=\dfrac{1}{\sqrt{1-y^{2}}}$
 
D'où, (arcsin)′(x)=11−x2
$\centerdot\ \ $ Soit $g(x)=\cos x\ $ alors, $D_{g}=\mathbb{R}.$
 
$T=2\pi\ $ et $\ g$ est paire donc on peut restreindre l'étudie sur $D_{E}=[0\;;\ \pi].$
 
On a : $g'(x)=-\sin x$ et soit le tableau de variation de $g$ suivant :
x0πg′(x)−1g↘−1
Ainsi, $g$ est continue et strictement décroissante sur $\left[0\;;\ \pi\right]$ donc $g$ est une bijection de $\left[0\;;\ \pi\right]$ vers $[-1\;;\ 1].$
 
D'où, $g$ admet une bijection réciproque $g^{-1}$, notée $\arccos$, qui est continue et strictement décroissante de $[-1\;;\ 1]$ vers $\left[0\;;\ \pi\right]$ et $\arccos$ est dérivable sur $]-1\;;\ 1[$ et on a : (g−1)′(y)=1g′(x)=1−sin⁡x
Or, 
 
$cos2⁡x+sin2⁡x=1⇒sin⁡x=±1−cos2⁡x=+1−cos2⁡xcar  x∈[0; π]⇒sin⁡x=1−y2$
 
Par suite, $(g^{-1})'(y)=\dfrac{1}{-\sqrt{1-y^{2}}}$
 
D'où, (arccos)′(x)=−11−x2
$\centerdot\ \ $ Soit $h(x)=\tan x\ $ alors, $D_{h}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi\right\}$
 
$h$ est $\pi-$périodique et impaire alors on choisit comme domaine d'étude l'intervalle suivant : $D_{E}=\left[0\;;\ \dfrac{\pi}{2}\right[.$
 
On a : $h'(x)=1+\tan^{2}x>0$ donc $h$ est croissante.
 
Tableau de variation de $h$ :
x0π/2h′(x)++∞h↗0
Donc, $h$ est continue et strictement croissante sur $\left[0\;;\ \dfrac{\pi}{2}\right[.$
 
Par suite, $h$ est une bijection de $\left[0\;;\ \dfrac{\pi}{2}\right[$ vers $[0\;;\ +\infty[.$
 
Par conséquent, $h$ admet une bijection réciproque $h^{-1}$, notée $\arctan$, qui est continue et strictement croissante de $[0\;;\ +\infty[$ vers $\left[0\;;\ \dfrac{\pi}{2}\right[$ et $\arctan$ est dérivable sur $[0\;;\ +\infty[$ et on a : (h−1)′(y)=1h′(x)=11+tan2⁡x
Or, $y=\tan x$
 
Donc, $(h^{-1})'(y)=\dfrac{1}{1+y^{2}}$
 
D'où, (arctan)′(x)=11+x2

Exercice d'application

Soit $f$ la fonction définie par : $f(x)=\sin^{2}x$
 
1) Montrer que $f$ admet une bijection réciproque sur $[0\;;\ 1]$
 
2) Donner l'expression de $(f^{-1})'(x)$

Résolution

1) On a : $f(x)=\sin^{2}x=\dfrac{1-\cos 2x}{2}\ $ alors, $D_{f}=\mathbb{R}$ et $T=\pi.$
 
De plus, $f$ est paire donc, on peut restreindre l'étude sur $D_{E}=\left[0\;;\ \dfrac{\pi}{2}\right].$
 
On a : $f'(x)=2\sin x\cos x\geq 0\;;\ \forall\;x\in D_{E}$ donc $f$ est croissante.
 
Tableau de variation de $f$ :
x0π/2f′(x)+1f↗0
Donc, $f$ est continue et strictement croissante sur $\left[0\;;\ \dfrac{\pi}{2}\right].$
 
Ainsi, $f$ est une bijection de $\left[0\;;\ \dfrac{\pi}{2}\right]$ vers $[0\;;\ 1].$
 
Par conséquent, $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement croissante de $[0\;;\ 1]$ vers $\left[0\;;\ \dfrac{\pi}{2}\right].$
 
2) Expression de $(f^{-1})'(x)$
 
On a : $f^{-1}$ est dérivable sur $]0\;;\ 1[$ et ∀y∈]0; 1[; (f−1)′(y)=1f′(x)=12sin⁡xcos⁡x
 
Or, 
 
$y=sin2⁡x⇒sin⁡x=±y=+ycar  x∈[0; π2]⇒sin⁡x=y$
 
et
 
$cos2⁡x+sin2⁡x=1⇒cos⁡x=±1−sin2⁡x=+1−sin2⁡xcar  x∈[0; π2]⇒cos⁡x=1−y$
 
Ce qui donne, $(f^{-1})'(y)=\dfrac{1}{2\sqrt{y}\sqrt{1-y}}$
 
D'où, $\boxed{(f^{-1})'(x)=\dfrac{1}{2\sqrt{x-x^{2}}}}$

III.4. Inégalité des accroissements finis

Théorème 6

Si une fonction $f$ est dérivable sur un intervalle $I$ de $\mathbb{R}\;;\ a\;,\ b\in I$ et si $\forall\;x\in[a\;;\ b]$ il existe $\;m\;,\ M\in\mathbb{R}$ tels que $m\leq f'(x)\leq M$ alors m(b−a)≤f(b)−f(a)≤M(b−a)
 
Preuve théorème
 
Soit $\varphi$ la fonction définie par $\varphi(x)=f(x)-mx.$
 
On a : $\varphi$ dérivable sur $[a\;;\ b]$ et $\varphi'(x)=f'(x)-m\geq 0.$
 
$\varphi$ est donc croissante.
 
Ainsi, 
 
$b≥a⇒φ(b)≥φ(a)⇒f(b)−mb≥f(a)−ma⇒f(b)−f(a)≥mb−ma=m(b−a)$
 
Par ailleurs, considérons $\psi$ la fonction définie par $\psi(x)=f(x)-Mx.$
 
Alors, $\psi$ est dérivable sur $[a\;;\ b]$ et $\psi'(x)=f'(x)-M\leq 0$ donc $\psi$ est décroissante.
 
Ainsi, 
 
$b≥a⇒ψ(b)≤ψ(a)⇒f(b)−Mb≤f(a)−Ma⇒f(b)−f(a)≤Mb−Ma=M(b−a)$
 
D'où, $m(b-a)\leq f(b)-f(a)\leq M(b-a)$

Corollaire

Si une fonction $f$ est dérivable sur $I\;;\ a\;,\ b\in I$ et s'il existe $k\in\mathbb{R}_{+}^{*}$ tel que $\forall\;x\in[a\;;\ b]\;;\ |f'(x)|\leq k$ alors |f(b)−f(a)|≤k|b−a|

Exercice d'application

Montrer que $\forall\;a\in\left[0\;;\ \dfrac{\pi}{4}\right]\;;\quad a\leq\tan a\leq 2a$

Résolution

Soit $f(x)=\tan x\ $ alors, $D_{f}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi\right\}$
 
De plus, $f$ est dérivable sur $\left[0\;;\ \dfrac{\pi}{4}\right]$ et $f'(x)=\dfrac{1}{\cos^{2}x}$
 
Soit $a\in\left[0\;;\ \dfrac{\pi}{4}\right]$ alors, $\forall\;x\in[0\;;\ a]$ on a : $\cos\left(\dfrac{\pi}{4}\right)\leq\cos a\leq\cos x\leq\cos 0$ 
 
c'est-à-dire ; $\dfrac{\sqrt{2}}{2}\leq\cos x\leq 1\ \Rightarrow\ \dfrac{1}{2}\leq\cos^{2}x\leq 1$
 
Donc, $1\leq\dfrac{1}{\cos^{2}x}\leq 2$
 
Par suite, en appliquant l'inégalité des accroissements finis on obtient : 
 
$1(a-0)\leq\tan a-\tan 0\leq 2(a-0)$
 
Ce qui donne, $a\leq\tan a\leq 2a$
 
Ainsi, $\forall\;a\in\left[0\;;\ \dfrac{\pi}{4}\right]\;;$ on a : $a\leq\tan a\leq 2a$
 
Auteur: 
Seyni Ndiaye & D. Faye

Commentaires

Ababacar (non vérifié)

mar, 08/04/2020 - 13:43

Vraiment je vs felicite de cet excellent travail

Ajouter un commentaire