Dérivabilité - T S
Classe:
Terminale
I. Nombre dérivé
I.1. Définitions
$-\ \ $ On dit qu'une fonction $f$ est dérivable en $x_{0}\in D_{f}$ si, et seulement si, l'une des conditions équivalentes suivantes est vérifiée.
$\centerdot\ \ C_{1}\ :\ \lim\limits_{x\rightarrow x_{0}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=\ell\in\mathbb{R}$ (réel fini)
$\centerdot\ \ C_{2}\ :\ \lim\limits_{h\rightarrow 0}\dfrac{f(x_{0}+h)-f(x_{0})}{h}=\ell\in\mathbb{R}$
$\centerdot\ \ C_{3}\ :\ $ il existe un réel $\ell$ et une fonction $\varepsilon$ tels que $$f(x_{0}+h)=f(x_{0})+\ell h+h\varepsilon(h)\quad\text{avec } \lim\limits_{h\rightarrow 0}\varepsilon(h)=0$$
Dans ce dernier cas on dit que $f$ admet un développement limité d'ordre 1 au voisinage de $x_{0}.$
$\ell$ est le nombre dérivé de $f$ en $x_{0}$ noté $f'(x_{0}).$
$$f'(x_{0})=\ell$$
$-\ \ $ On dit qu'une fonction $f$ est dérivable à gauche de $x_{0}\in D_{f}$ si, et seulement si,
$$\lim\limits_{x\rightarrow x_{0}^{-}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=\ell_{1}\in\mathbb{R}\quad\text{(réel fini)}$$
$\ell_{1}$ est le nombre dérivé de $f$ à gauche de $x_{0}$ noté $f'_{g}(x_{0}).$
$$f'_{g}(x_{0})=\ell_{1}$$
$-\ \ $ On dit qu'une fonction $f$ est dérivable à droite de $x_{0}\in D_{f}$ si, et seulement si,
$$\lim\limits_{x\rightarrow x_{0}^{+}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=\ell_{2}\in\mathbb{R}\quad\text{(réel fini)}$$
$\ell_{2}$ est le nombre dérivé de $f$ à droite de $x_{0}$ noté $f'_{d}(x_{0}).$
$$f'_{d}(x_{0})=\ell_{2}$$
Théorème 1
Une fonction $f$ est dérivable en $x_{0}$ si, et seulement si, $f$ est dérivable à gauche et à droite de $x_{0}$ et que les nombres dérivés sont égaux $(f'_{g}(x_{0})=f'_{d}(x_{0}))$
Exercice d'application
Soit $f$ et $g$ deux fonctions définies par : $$f(x)=|x^{2}-x|\quad\text{et}\quad g(x)=\sqrt{x^{2}-4x+3}$$
Étudier la dérivabilité de $f$ et $g$ en 1.
Résolution
Dérivabilité de $f$ en 1
Écrivons $f$ sans le symbole des valeurs absolues en utilisant le tableau de signe suivant :
$$\begin{array}{|c|lcccccr|}\hline x&-\infty&&0&&1&&+\infty\\ \hline x^{2}-x&&+&0&-&0&+&\\ \hline|x^{2}-x|&&x^{2}-x&|&-x^{2}+x&|&x^{2}-x&\\ \hline \end{array}$$
Donc,
$\begin{array}{rcl}\lim\limits_{x\rightarrow 1^{-}}\dfrac{f(x)-f(1)}{x-1}&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{-x^{2}+x}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}(-x)\\ \\&=&-1 \end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow 1^{+}}\dfrac{f(x)-f(1)}{x-1}&=&\lim\limits_{x\rightarrow 1^{+}}\dfrac{x^{2}-x}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{+}}(x)\\ \\&=&1 \end{array}$
Ainsi, $f'_{g}(1)\neq f'_{d}(1)$
D'où, $f$ n'est pas dérivable en 1.
Dérivabilité de $g$ en 1
D'après le tableau de signes ci-dessous on a $D_{g}=]-\infty\;;\ 1]\cup[3\;;\ +\infty[$
$$\begin{array}{|c|lcccccr|}\hline x&-\infty&&1&&3&&+\infty\\ \hline x^{2}-4x+3&&+&0&-&0&+&\\ \hline \end{array}$$
Alors,
$\begin{array}{rcl}\lim\limits_{x\rightarrow 1^{-}}\dfrac{g(x)-g(1)}{x-1}&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{\sqrt{x^{2}-4x+3}}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{(x-1)(x-3)}{(x-1)\sqrt{x^{2}-4x+3}}\\ \\&=&-\infty \end{array}$
Donc, $g$ non dérivable en $1.$
I.2. Interprétation géométrique de la dérivabilité
Nous distinguons deux cas :
$\centerdot\ \ $ Soit $f$ dérivable en $x_{0}$ alors $\lim\limits_{x\rightarrow x_{0}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=f'(x_{0})\in\mathbb{R}$
On a : $\lim\limits_{h\rightarrow 0}\dfrac{f(x_{0}+h)-f(x_{0})}{h}$ est le coefficient directeur de la sécante $(AB).$
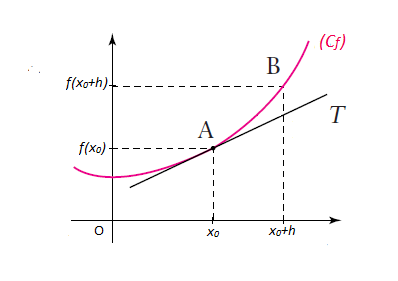
Alors, lorsque $h$ tend vers $0$ le point $B$ tend vers le point $A.$
Et par conséquent, la droite $(AB)$ tend vers une droite dite limite $(T)$ appelée tangente à $C_{f}$ en $x_{0}.$
Ainsi, au point d'abscisse $x_{0}$ on a une tangente $(T)$ d'équation : $$y=f'(x_{0})(x-x_{0})+f(x_{0})$$
$f'(x_{0})$ est le coefficient directeur de la tangente.
$\centerdot\ \ $ Soit $f$ non dérivable en $x_{0}$ ; les cas suivants peuvent alors se présenter :
$-\ \ $ deux demi-tangentes au point d'abscisse $x_{0}.$
Par exemple $f'_{g}(x_{0})=-2\ $ et $\ f'_{d}(x_{0})=\dfrac{2}{3}$
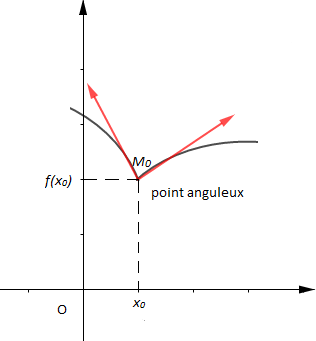
Les équations des demi-tangentes sont données par :
$T_{1}\ :\ y=f'_{g}(x_{0})(x-x_{0})+f(x_{0})$ avec $f'_{g}(x_{0})=-2$
$T_{2}\ :\ y=f'_{d}(x_{0})(x-x_{0})+f(x_{0})$ avec $f'_{d}(x_{0})=\dfrac{2}{3}$
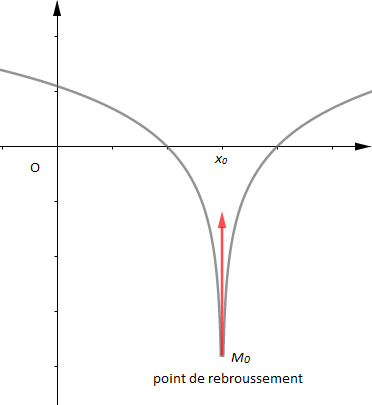
$-\ \ $ une demi-tangente verticale au point d'abscisse $x_{0}.$
Par exemple :
$\lim\limits_{x\rightarrow x_{0}^{-}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=-\infty\ $ et $\ \lim\limits_{x\rightarrow x_{0}^{+}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=+\infty$
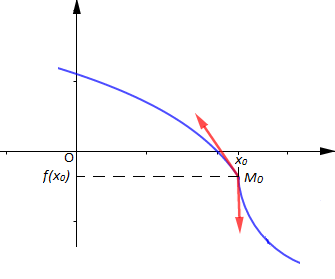
$-\ \ $ une demi-tangente de pente fini et une demi-tangente verticale au point d'abscisse $x_{0}.$
Par exemple :
$f'_{g}(x_{0})=-2\ $ et $\ \lim\limits_{x\rightarrow x_{0}^{+}}\dfrac{f(x)-f(x_{0})}{x-x_{0}}=+\infty$
I.3. Opérations sur la dérivabilité
Théorème 2
Si une fonction $f$ est dérivable en $x_{0}$ alors $f$ est continue en $x_{0}$ ; la réciproque est fausse.
Par exemple la fonction $f(x)=|x^{2}-x|$ qui est continue en $1$ et non dérivable en $1.$
Preuve théorème
$f$ dérivable en $x_{0}$ alors il existe une fonction $\varepsilon$ telle que $$f(x_{0}+h)=f(x_{0})+hf'(x_{0})+h\varepsilon(h)\quad\text{avec } \lim_{h\rightarrow 0}\varepsilon(h)=0$$
Posons $x=x_{0}+h$ donc, $f(x)=f(x_{0})+(x-x_{0})f'(x_{0})+(x-x_{0})\varepsilon(x-x_{0})$
Ainsi,
$\begin{array}{rcl}\lim\limits_{x\rightarrow x_{0}}f(x)&=&\lim\limits_{x\rightarrow x_{0}}f(x_{0})+(x-x_{0})f'(x_{0})+(x-x_{0})\varepsilon(x-x_{0})\\ \\&=&f(x_{0})\end{array}$
D'où, $f$ continue en $x_{0}$
Théorème 3
Si $f$ et $g$ sont deux fonctions dérivables en $x_{0}$ alors :
$\centerdot\ \ f+g$ est dérivables en $x_{0}$ et $$(f+g)'(x_{0})=f'(x_{0})+g'(x_{0})$$
$\centerdot\ \ fg$ est dérivables en $x_{0}$ et $$(fg)'(x_{0})=f'(x_{0})g(x_{0})+f(x_{0})g'(x_{0})$$
$\centerdot\ \ $ si de plus $g(x)\neq 0$ alors $\dfrac{f}{g}$ est dérivables en $x_{0}$ et $$\left(\dfrac{f}{g}\right)'(x_{0})=\dfrac{f'(x_{0})g(x_{0})-f(x_{0})g'(x_{0})}{(g(x_{0}))^{2}}$$
Théorème 4 (composée)
Si une fonction $f$ est dérivable en $x_{0}\ $ et $\ g$ dérivable en $y_{0}=f(x_{0}$ alors $g\circ f$ est dérivable en $x_{0}$ et $$(g\circ f)'(x_{0})=f'(x_{0})\times g'[f(x_{0})]$$
II. Fonctions dérivées
II.1. Définition
On appelle fonction dérivée de $f$ la fonction notée $f'$ qui associe à tout $x$ son nombre dérivé.
II.2. Tableau de dérivées
$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline f&f'&f&f'&f&f'&f&f'\\ \hline k\in\mathbb{R}&0&\sin x&\cos x&\dfrac{1}{u}&-\dfrac{u'}{u^{2}}&\tan u&\dfrac{u'}{\cos^{2}u}\\ \hline ax&a&\cos x&-\sin x&\sqrt{u}&\dfrac{u'}{2\sqrt{u}}&u^{n}&nu'u^{n-1}\\ \hline \dfrac{1}{x}&-\dfrac{1}{x^{2}}&\tan x&\dfrac{1}{\cos^{2}x}&\sin u&u'\cos u&\dfrac{u}{v}&\dfrac{u'v-uv'}{v^{2}}\\ \hline \sqrt{x}&\dfrac{1}{2\sqrt{x}}&x^{n}&nx^{n-1}&\cos u&-u'\sin u&uv&u'v+uv'\\ \hline \end{array}$$
$u$ une fonction dérivable
Exercice d'application
Calculer les dérivées des fonctions $f\ $ et $\ g$ définies par :
$f(x)=(x-1)\sqrt{x^{2}-4x+3}\;,\ g(x)=\sin^{4}(4x^{2}-3x+5)$
Résolution
Soit $f(x)=(x-1)\sqrt{x^{2}-4x+3}\ $ alors sa dérivée $f'(x)$ est donnée par :
$\begin{array}{rcl} f'(x)&=&\sqrt{x^{2}-4x+3}+(x-1)\times\dfrac{2x-4}{2\sqrt{x^{2}-4x+3}}\\ \\&=&\sqrt{x^{2}-4x+3}+\dfrac{(x-1)(x-2)}{\sqrt{x^{2}-4x+3}}\\ \\&=&\dfrac{x^{2}-4x+3+x^{2}-3x+2}{\sqrt{x^{2}-4x+3}}\end{array}$
D'où, $f'(x)=\dfrac{2x^{2}-7x+5}{\sqrt{x^{2}-4x+3}}$
On a $g(x)=\sin^{4}(4x^{2}-3x+5)$
alors, $g'(x)=4(8x-3)\cos(4x^{2}-3x+5)\sin^{3}(4x^{2}-3x+5)$
II.3. Dérivées successives
$\centerdot\ \ $ Si $f$ est dérivable sur $I$ et si sa fonction dérivée $f'$ est dérivable sur $I$ on dira que $f$ est deux fois dérivable sur $I$ et la dérivée seconde est notée $f''(x)$
$\centerdot\ \ $ Si $f''$ est dérivable sur $I$ on dira que $f$ est trois fois dérivable sur $I$ et la dérivée troisième est notée $f^{(3)}(x)$
$\centerdot\ \ $ Si $f$ est $n$ fois dérivable sur $I$ sa dérivée $n^{\text{ième}}$ est notée $f^{(n)}(x)$
Par exemple, la dérivée $n^{\text{ième}}$ des fonctions $f(x)=\sin x$ et $g(x)=\cos x$ est donnée par : $$f^{(n)}(x)=\sin\left(x+\dfrac{n\pi}{2}\right)\;,\quad g^{(n)}(x)=\cos\left(x+\dfrac{n\pi}{2}\right)$$
$\centerdot\ \ $ Si $f$ et $g$ sont $n$ fois dérivable sur $I$ alors, $$(fg)^{(n)}=\sum_{k=0}^{n}C_{n}^{k}f^{(k)}(x)g^{(n-k)}(x)$$
III. Applications
III.1. Sens de variation
$\centerdot\ \ $ Si $f'(x)\geq 0$ sur $I$ alors, $f$ est croissante sur $I.$
$\centerdot\ \ $ Si $f'(x)\leq 0$ sur $I$ alors, sur $I$, alors $f$ est décroissante sur $I.$
$\centerdot\ \ $ Si $f'(x)=0$ sur $I$ alors, la fonction $f$ est constante sur $I.$
$\centerdot\ \ $ Si $f'(x)>0$ sur $I$ alors, $f$ est strictement croissante sur $I.$
$\centerdot\ \ $ Si $f'(x)<0$ sur $I$ alors, sur $I$, alors $f$ est strictement décroissante sur $I.$
Exercice d'application
Soit $f$ la fonction définie par : $f(x)=|x^{2}-x|$
1) Déterminer les limites aux bornes de $D_{f}$
2) Étudier la dérivabilité en 0 et 1
3) Donner la dérivée et dresser le tableau de variation
Résolution
1) Soit $f(x)=|x^{2}-x|$ alors, $D_{f}=\mathbb{R}$ et en écrivant $f$ sans le symbole des valeurs absolues on obtient :
$$f(x)=\left\lbrace\begin{array}{rcl} x^{2}-x&\text{si}&x\in\;]-\infty\;;\ 0]\cup[1\;;\ +\infty[\\-x^{2}+x&\text{si}&x\in\;]0\;;\ 1[\end{array}\right.$$
Ainsi,
$\begin{array}{rcl}\lim\limits_{x\rightarrow -\infty}f(x)&=&\lim\limits_{x\rightarrow -\infty}x^{2}-x\\\\&=&+\infty\end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}f(x)&=&\lim\limits_{x\rightarrow +\infty}x^{2}-x\\\\&=&+\infty\end{array}$
2) Dérivabilité de $f$ en $0$
On a
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{-}}\dfrac{f(x)-f(0)}{x-0}&=&\lim\limits_{x\rightarrow 0^{-}}\dfrac{x^{2}-x}{x}\\ \\&=&\lim\limits_{x\rightarrow 0^{-}}(x-1)\\ \\&=&-1 \end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{-x^{2}+x}{x}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}(-x+1)\\ \\&=&1 \end{array}$
Ainsi, $f'_{g}(0)\neq f'_{d}(0)$
D'où, $f$ n'est pas dérivable en $0.$
Dérivabilité de $f$ en $1$
On a
$\begin{array}{rcl}\lim\limits_{x\rightarrow 1^{-}}\dfrac{f(x)-f(1)}{x-1}&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{-x^{2}+x}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}(-x)\\ \\&=&-1 \end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow 1^{+}}\dfrac{f(x)-f(1)}{x-1}&=&\lim\limits_{x\rightarrow 1^{+}}\dfrac{x^{2}-x}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{+}}(x)\\ \\&=&1 \end{array}$
Ainsi, $f'_{g}(1)\neq f'_{d}(1)$
D'où, $f$ n'est pas dérivable en $1.$
3) Soit $f'(x)$ la fonction dérivée de $f$ alors on a : $$f(x)=\left\lbrace\begin{array}{rcl} 2x-1&\text{si}&x\in\;]-\infty\;;\ 0[\cup]1\;;\ +\infty[\\-2x+1&\text{si}&x\in\;]0\;;\ 1[\end{array}\right.$$
Tableau de variation de $f$
$$\begin{array}{|c|lcccccccr|}\hline x&-\infty&&0&&1/2&&1&&+\infty\\ \hline f'(x)&&-&-1||1&+&0&-&-1||1&+&\\ \hline&-\infty&&&&1/4&&&&+\infty\\f&&\searrow&&\nearrow&&\searrow&&\nearrow&\\&&&0&&&&0&&\\ \hline \end{array}$$
III.2. Extrémums - point d'inflexion
$\centerdot\ \ $ On dit qu'une fonction $f$ présente un extrémum au point d'abscisse $x_{0}$ si $f'(x)$ s'annule en $x_{0}$ en changeant de signe autour de $x_{0}.$
$$\begin{array}{|c|lcccr|}\hline x&&&x_{0}&&\\ \hline f'(x)&&-&0&+&\\ \hline&&&|&&\\f&&\searrow&|&\nearrow&\\&&&\text{minimum}&&\\ \hline \end{array}$$
On peut aussi formuler ainsi :
Il existe $\alpha>0$ tel que $\forall\;x\in\;]x_{0}-\alpha\;;\ x_{0}+\alpha[\;,\quad f(x)\geq f(x_{0})$
$$\begin{array}{|c|lcccr|}\hline x&&&x_{0}&&\\ \hline f'(x)&&+&0&-&\\ \hline&&&\text{maximum}&&\\f&&\nearrow&|&\searrow&\\&&&|&&\\ \hline \end{array}$$
On peut alors formuler ainsi :
Il existe $\alpha>0$ tel que $\forall\;x\in\;]x_{0}-\alpha\;;\ x_{0}+\alpha[\;,\quad f(x)\leq f(x_{0})$
$\centerdot\ \ $ On dit que $M_{0}\begin{pmatrix} x_{0}\\y_{0}\end{pmatrix}$ est une point d'inflexion si :
$\ast\ \ f'(x)$ garde un signe constant autour de $x_{0}$
$\ast\ \ f''(x)$ s'annule en $x_{0}$ en changeant de signe.
Par exemple
$$\begin{array}{|c|lcccr|}\hline x&&&x_{0}&&\\ \hline f''(x)&&+&0&-&\\ \hline f'(x)&&+&|&+&\\ \hline \end{array}\quad\text{ou}\quad\begin{array}{|c|lcccr|}\hline x&&&x_{0}&&\\ \hline f''(x)&&+&0&-&\\ \hline f'(x)&&-&|&-&\\ \hline \end{array}$$
ou encore
$$\begin{array}{|c|lcccr|}\hline x&&&x_{0}&&\\ \hline f''(x)&&-&0&+&\\ \hline f'(x)&&+&|&+&\\ \hline \end{array}\quad\text{ou}\quad\begin{array}{|c|lcccr|}\hline x&&&x_{0}&&\\ \hline f''(x)&&-&0&+&\\ \hline f'(x)&&-&|&-&\\ \hline \end{array}$$
Remarque : un point d'inflexion est un point où la courbe traverse sa tangente.
III.3. Dérivée de la réciproque d'une fonction
III.3.1. Théorème 5 : bijection
Si $f$ est une fonction continue et strictement monotone sur $I$ alors $f$ est une bijection de $I$ vers $J=f(I)$ et donc $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement monotone dans le même sens que $f$ de $J$ vers $I$ et $f^{-1}$ est dérivable sur $J_{1}=J\setminus\{y\in J\;/\;f'(f^{-1}(y))=0\}$ et on a : $$\forall\;y_{0}\in J_{1}\;;\ (f^{-1})'(y_{0})=\dfrac{1}{f'(x_{0})}$$
où $f(x_{0})=y_{0}\;;\ x_{0}\in I.$
Remarque : pour obtenir $x_{0}$ on résout l'équation $f(x)=y_{0}$
Exercice d'application
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x^{3}-3x+1$
1) Montrer que $f$ admet une bijection réciproque sur $[1\;;\ +\infty[$
2) Calculer $(f^{-1})'(1)$
Résolution
1) Soit $f(x)=x^{3}-3x+1$ alors, $f'(x)=3x^{2}-3=3(x-1)(x+1)$
Donc, $f'(x)$ positive sur $]-\infty\;;\ -1[\cup]1\;;\ +\infty[$ et négative sur $]-1\;;\ 1[.$
$\begin{array}{rcl}\lim\limits_{x\rightarrow -\infty}f(x)&=&\lim\limits_{x\rightarrow -\infty}x^{3}-3x+1\\\\&=&-\infty\end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}f(x)&=&\lim\limits_{x\rightarrow +\infty}x^{3}-3x+1\\\\&=&+\infty\end{array}$
Tableau de variation de $f$
$$\begin{array}{|c|lcccccr|}\hline x&-\infty&&-1&&1&&+\infty\\ \hline f'(x)&&+&0&-&0&+&\\ \hline&&&3&&&&+\infty\\f&&\nearrow&&\searrow&&\nearrow&\\&-\infty&&&&-1&&\\ \hline \end{array}$$
Ainsi, $f$ est continue et strictement croissante sur $[1\;;\ +\infty[$ donc bijective de $[1\;;\ +\infty[$ vers $[-1\;;\ +\infty[.$
Par suite $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement croissante de $[-1\;;\ +\infty[$ vers $[1\;;\ +\infty[$ et $f^{-1}$ est dérivable sur $]-1\;;\ +\infty[.$
2) Calculons $(f^{-1})'(1)$
On a : $(f^{-1})'(1)=\dfrac{1}{f'(x_{0})}$ avec $f^{-1}(1)=x_{0}$ ; c'est-à-dire $f(x_{0})=1.$
Donc, résolvons l'équation $f(x)=1.$ On a :
$\begin{array}{rcl} f(x)=1&\Leftrightarrow&x^{3}-3x+1=1\\\\&\Leftrightarrow&x^{3}-3x=0\\\\&\Leftrightarrow&x=0\quad\text{ou}\quad x=-\sqrt{3}\quad\text{ou}\quad x=\sqrt{3}\end{array}$
Or, $\sqrt{3}$ est l'unique solution qui appartient à $[1\;;\ +\infty[$ donc, $x_{0}=\sqrt{3}.$
Par suite,
$\begin{array}{rcl} (f^{-1})'(1)=\dfrac{1}{f'(x_{0})}&=&\dfrac{1}{f'(\sqrt{3})}\\ \\&=&\dfrac{1}{3\times 3-3}\\ \\&=&\dfrac{1}{6}\end{array}$
D'où, $(f^{-1})'(1)=\dfrac{1}{6}$
III.3.2. Dérivée des fonctions réciproques de : $\sin x\;;\ \cos x\;;\ \tan x$
$\centerdot\ \ $ Soit $f(x)=\sin x\ $ alors, $D_{f}=\mathbb{R}$ et $T=2\pi.$
$f$ impaire donc le domaine d'étude est donné par $D_{E}=[0\;;\ \pi].$
Soit $f'(x)=\cos x$ alors le tableau de variation de $f$ est :
$$\begin{array}{|c|lcccr|}\hline x&0&&\pi/2&&\pi\\ \hline f'(x)&&+&0&-&\\ \hline&&&1&&\\f&&\nearrow&&\searrow&\\&0&&&&0\\ \hline \end{array}$$
Ainsi, $f$ est continue et strictement croissante sur $\left[0\;;\ \dfrac{\pi}{2}\right]$ donc $f$ est une bijection de $\left[0\;;\ \dfrac{\pi}{2}\right]$ vers $[0\;;\ 1].$
D'où, $f$ admet une bijection réciproque $f^{-1}$, notée $\arcsin$, qui est continue et strictement croissante de $[0\;;\ 1]$ vers $\left[0\;;\ \dfrac{\pi}{2}\right]$ et $\arcsin$ est dérivable sur $[0\;;\ 1[$ et on a : $$(f^{-1})'(y)=\dfrac{1}{f'(x)}=\dfrac{1}{\cos x}$$
Or,
$\begin{array}{rcrcl}\cos^{2}x+\sin^{2}x=1&\Rightarrow&\cos x&=&\pm\sqrt{1-\sin^{2}x}\\\\&&&=&+\sqrt{1-\sin^{2}x}\quad\text{car }\ x\in\left[0\;;\ \dfrac{\pi}{2}\right]\\\\&\Rightarrow&\cos x&=&\sqrt{1-y^{2}}\end{array}$
Ce qui entraîne alors, $(f^{-1})'(y)=\dfrac{1}{\sqrt{1-y^{2}}}$
D'où, $$\boxed{(\arcsin)'(x)=\dfrac{1}{\sqrt{1-x^{2}}}}$$
$\centerdot\ \ $ Soit $g(x)=\cos x\ $ alors, $D_{g}=\mathbb{R}.$
$T=2\pi\ $ et $\ g$ est paire donc on peut restreindre l'étudie sur $D_{E}=[0\;;\ \pi].$
On a : $g'(x)=-\sin x$ et soit le tableau de variation de $g$ suivant :
$$\begin{array}{|c|lcr|}\hline x&0&&\pi\\ \hline g'(x)&&-&\\ \hline&1&&\\g&&\searrow&\\&&&-1\\ \hline \end{array}$$
Ainsi, $g$ est continue et strictement décroissante sur $\left[0\;;\ \pi\right]$ donc $g$ est une bijection de $\left[0\;;\ \pi\right]$ vers $[-1\;;\ 1].$
D'où, $g$ admet une bijection réciproque $g^{-1}$, notée $\arccos$, qui est continue et strictement décroissante de $[-1\;;\ 1]$ vers $\left[0\;;\ \pi\right]$ et $\arccos$ est dérivable sur $]-1\;;\ 1[$ et on a : $$(g^{-1})'(y)=\dfrac{1}{g'(x)}=\dfrac{1}{-\sin x}$$
Or,
$\begin{array}{rcrcl}\cos^{2}x+\sin^{2}x=1&\Rightarrow&\sin x&=&\pm\sqrt{1-\cos^{2}x}\\\\&&&=&+\sqrt{1-\cos^{2}x}\quad\text{car }\ x\in\left[0\;;\ \pi\right]\\\\&\Rightarrow&\sin x&=&\sqrt{1-y^{2}}\end{array}$
Par suite, $(g^{-1})'(y)=\dfrac{1}{-\sqrt{1-y^{2}}}$
D'où, $$\boxed{(\arccos)'(x)=-\dfrac{1}{\sqrt{1-x^{2}}}}$$
$\centerdot\ \ $ Soit $h(x)=\tan x\ $ alors, $D_{h}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi\right\}$
$h$ est $\pi-$périodique et impaire alors on choisit comme domaine d'étude l'intervalle suivant : $D_{E}=\left[0\;;\ \dfrac{\pi}{2}\right[.$
On a : $h'(x)=1+\tan^{2}x>0$ donc $h$ est croissante.
Tableau de variation de $h$ :
$$\begin{array}{|c|lcr||}\hline x&0&&\pi/2\\ \hline h'(x)&&+&\\ \hline&&&+\infty\\h&&\nearrow&\\&0&&\\ \hline \end{array}$$
Donc, $h$ est continue et strictement croissante sur $\left[0\;;\ \dfrac{\pi}{2}\right[.$
Par suite, $h$ est une bijection de $\left[0\;;\ \dfrac{\pi}{2}\right[$ vers $[0\;;\ +\infty[.$
Par conséquent, $h$ admet une bijection réciproque $h^{-1}$, notée $\arctan$, qui est continue et strictement croissante de $[0\;;\ +\infty[$ vers $\left[0\;;\ \dfrac{\pi}{2}\right[$ et $\arctan$ est dérivable sur $[0\;;\ +\infty[$ et on a : $$(h^{-1})'(y)=\dfrac{1}{h'(x)}=\dfrac{1}{1+\tan^{2}x}$$
Or, $y=\tan x$
Donc, $(h^{-1})'(y)=\dfrac{1}{1+y^{2}}$
D'où, $$\boxed{(\arctan)'(x)=\dfrac{1}{1+x^{2}}}$$
Exercice d'application
Soit $f$ la fonction définie par : $f(x)=\sin^{2}x$
1) Montrer que $f$ admet une bijection réciproque sur $[0\;;\ 1]$
2) Donner l'expression de $(f^{-1})'(x)$
Résolution
1) On a : $f(x)=\sin^{2}x=\dfrac{1-\cos 2x}{2}\ $ alors, $D_{f}=\mathbb{R}$ et $T=\pi.$
De plus, $f$ est paire donc, on peut restreindre l'étude sur $D_{E}=\left[0\;;\ \dfrac{\pi}{2}\right].$
On a : $f'(x)=2\sin x\cos x\geq 0\;;\ \forall\;x\in D_{E}$ donc $f$ est croissante.
Tableau de variation de $f$ :
$$\begin{array}{|c|lcr|}\hline x&0&&\pi/2\\ \hline f'(x)&&+&\\ \hline&&&1\\f&&\nearrow&\\&0&&\\ \hline \end{array}$$
Donc, $f$ est continue et strictement croissante sur $\left[0\;;\ \dfrac{\pi}{2}\right].$
Ainsi, $f$ est une bijection de $\left[0\;;\ \dfrac{\pi}{2}\right]$ vers $[0\;;\ 1].$
Par conséquent, $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement croissante de $[0\;;\ 1]$ vers $\left[0\;;\ \dfrac{\pi}{2}\right].$
2) Expression de $(f^{-1})'(x)$
On a : $f^{-1}$ est dérivable sur $]0\;;\ 1[$ et $$\forall\;y\in\;]0\;;\ 1[\;;\ (f^{-1})'(y)=\dfrac{1}{f'(x)}=\dfrac{1}{2\sin x\cos x}$$
Or,
$\begin{array}{rcrcl} y=\sin^{2}x&\Rightarrow&\sin x&=&\pm\sqrt{y}\\\\&&&=&+\sqrt{y}\quad\text{car }\ x\in\left[0\;;\ \dfrac{\pi}{2}\right]\\\\&\Rightarrow&\sin x&=&\sqrt{y}\end{array}$
et
$\begin{array}{rcrcl}\cos^{2}x+\sin^{2}x=1&\Rightarrow&\cos x&=&\pm\sqrt{1-\sin^{2}x}\\\\&&&=&+\sqrt{1-\sin^{2}x}\quad\text{car }\ x\in\left[0\;;\ \dfrac{\pi}{2}\right]\\\\&\Rightarrow&\cos x&=&\sqrt{1-y}\end{array}$
Ce qui donne, $(f^{-1})'(y)=\dfrac{1}{2\sqrt{y}\sqrt{1-y}}$
D'où, $\boxed{(f^{-1})'(x)=\dfrac{1}{2\sqrt{x-x^{2}}}}$
III.4. Inégalité des accroissements finis
Théorème 6
Si une fonction $f$ est dérivable sur un intervalle $I$ de $\mathbb{R}\;;\ a\;,\ b\in I$ et si $\forall\;x\in[a\;;\ b]$ il existe $\;m\;,\ M\in\mathbb{R}$ tels que $m\leq f'(x)\leq M$ alors $$m(b-a)\leq f(b)-f(a)\leq M(b-a)$$
Preuve théorème
Soit $\varphi$ la fonction définie par $\varphi(x)=f(x)-mx.$
On a : $\varphi$ dérivable sur $[a\;;\ b]$ et $\varphi'(x)=f'(x)-m\geq 0.$
$\varphi$ est donc croissante.
Ainsi,
$\begin{array}{rcrcl} b\geq a&\Rightarrow&\varphi(b)&\geq&\varphi(a)\\\\&\Rightarrow&f(b)-mb&\geq&f(a)-ma\\\\&\Rightarrow&f(b)-f(a)&\geq&mb-ma=m(b-a)\end{array}$
Par ailleurs, considérons $\psi$ la fonction définie par $\psi(x)=f(x)-Mx.$
Alors, $\psi$ est dérivable sur $[a\;;\ b]$ et $\psi'(x)=f'(x)-M\leq 0$ donc $\psi$ est décroissante.
Ainsi,
$\begin{array}{rcrcl} b\geq a&\Rightarrow&\psi(b)&\leq&\psi(a)\\\\&\Rightarrow&f(b)-Mb&\leq&f(a)-Ma\\\\&\Rightarrow&f(b)-f(a)&\leq&Mb-Ma=M(b-a)\end{array}$
D'où, $m(b-a)\leq f(b)-f(a)\leq M(b-a)$
Corollaire
Si une fonction $f$ est dérivable sur $I\;;\ a\;,\ b\in I$ et s'il existe $k\in\mathbb{R}_{+}^{*}$ tel que $\forall\;x\in[a\;;\ b]\;;\ |f'(x)|\leq k$ alors $$|f(b)-f(a)|\leq k|b-a|$$
Exercice d'application
Montrer que $\forall\;a\in\left[0\;;\ \dfrac{\pi}{4}\right]\;;\quad a\leq\tan a\leq 2a$
Résolution
Soit $f(x)=\tan x\ $ alors, $D_{f}=\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+k\pi\right\}$
De plus, $f$ est dérivable sur $\left[0\;;\ \dfrac{\pi}{4}\right]$ et $f'(x)=\dfrac{1}{\cos^{2}x}$
Soit $a\in\left[0\;;\ \dfrac{\pi}{4}\right]$ alors, $\forall\;x\in[0\;;\ a]$ on a : $\cos\left(\dfrac{\pi}{4}\right)\leq\cos a\leq\cos x\leq\cos 0$
c'est-à-dire ; $\dfrac{\sqrt{2}}{2}\leq\cos x\leq 1\ \Rightarrow\ \dfrac{1}{2}\leq\cos^{2}x\leq 1$
Donc, $1\leq\dfrac{1}{\cos^{2}x}\leq 2$
Par suite, en appliquant l'inégalité des accroissements finis on obtient :
$1(a-0)\leq\tan a-\tan 0\leq 2(a-0)$
Ce qui donne, $a\leq\tan a\leq 2a$
Ainsi, $\forall\;a\in\left[0\;;\ \dfrac{\pi}{4}\right]\;;$ on a : $a\leq\tan a\leq 2a$
Auteur:
Seyni Ndiaye & D. Faye

Commentaires
Ababacar (non vérifié)
mar, 08/04/2020 - 13:43
Permalien
Vraiment je vs felicite de
Ajouter un commentaire