Comment montrer qu'un quadrilatère est un parallélogramme ? - 3e
Classe:
Troisième
Considérons un quadrilatère $ABCD.$ Pour montrer que ce quadrilatère est un parallélogramme, on procède comme suit :
I. En utilisant $(AB)//(DC)\ $ et $\ (AD)//(BC)$
Soit $ABCD$ un quadrilatère. Si $(AB)//(DC)\ $ et $\ (AD)//(BC)$ alors, $ABCD$ est un parallélogramme.
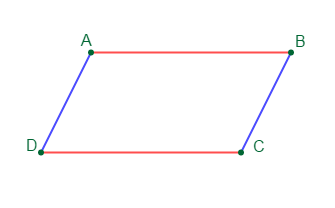
Donc, pour cette partie, il faut montrer que $(AB)//(DC)\ $ et $\ (AD)//(BC)$ en même temps pour conclure que $ABCD$ est parallélogramme.
Attention !
Dans le cas où $(AB)$ n'est pas parallèle à $(DC)$ ou encore $(AD)$ n'est pas parallèle à $(BC)$, on n'obtiendra pas un parallélogramme.
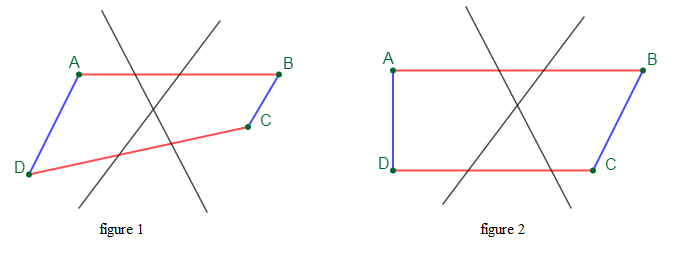
Sur la figure 1, on constate que $(AB)$ n'est pas parallèle à $(DC)$ donc, $ABCD$ n'est pas un parallélogramme.
De même, sur la figure 2, on remarque que $(AD)$ n'est pas parallèle à $(BC)$, ce qui signifie que $ABCD$ n'est pas un parallélogramme.
II. En utilisant l'argument $[AC]\ $ et $\ [BD]$ ont même milieu
$ABCD$ est quadrilatère. Si $[AC]\ $ et $\ [BD]$ ont le même milieu alors, on peut conclure que $ABCD$ est un parallélogramme.
Donc, il faut juste montrer que les diagonales du quadrilatère ont le même milieu pour conclure que $ABCD$ est un parallélogramme.
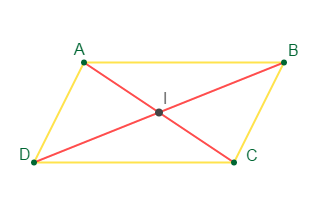
On constate que les diagonales $[AC]\ $ et $\ [BD]$ ont le même milieu $I$ donc, le quadrilatère $ABCD$ est un parallélogramme.
III. En utilisant $\overrightarrow{AB}=\overrightarrow{DC}\ $ ou $\ \overrightarrow{AD}=\overrightarrow{BC}$
Soit $ABCD$ un quadrilatère. Si $\overrightarrow{AB}=\overrightarrow{DC}\ $ ou si $\ \overrightarrow{AD}=\overrightarrow{BC}$ alors, on dira que $ABCD$ est un parallélogramme.
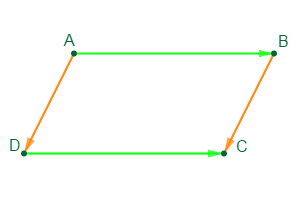
Donc, pour cette partie, il faut juste montrer que $\overrightarrow{AB}=\overrightarrow{DC}\ $ ou encore que $\ \overrightarrow{AD}=\overrightarrow{BC}$ pour enfin conclure que $ABCD$ est un parallélogramme.

Commentaires
Anonyme (non vérifié)
jeu, 08/06/2020 - 03:19
Permalien
Excellent
Anonyme (non vérifié)
mar, 12/29/2020 - 10:50
Permalien
excellent
Laye SAO (non vérifié)
lun, 04/12/2021 - 17:32
Permalien
Savoir et croire savoir, il y a un grand fosse.
Ousmane mboup (non vérifié)
ven, 04/23/2021 - 17:45
Permalien
Merci
Ajouter un commentaire