Série d'exercices : Repérage - 2nd
Classe:
Seconde
Mesures algébriques
Exercice 1
Les points $A\;,\ B\;,\ C$ et $D$ sont situés sur un axe de telle sorte que : $$\overline{AB}=-8\;;\quad \overline{BC}=12\ \text{ et }\ \overline{CD}=-6$$
Calculer $\overline{AC}\;,\ \overline{AD}\;,\ \overline{BA}\;,\ \overline{BD}\;,\ \overline{DA}$ et $\overline{DB}.$
Exercice 2
Sur un axe $(D)$, on donne trois points $A\;,\ B$ et $C$ tels que $\overline{AB}=-9$ et $\overline{BC}=16.$
Où faut-il placer l'origine $O$ pour que $$\overline{OA}+3\overline{OB}+5\overline{OC}=0\ ?$$
Exercice 3
Soient $A$ et $B$ deux points d'un axe, $I$ milieu de $[AB].$ Montrer que pour tout point $M$ de l'axe, on a :
a) $\overline{MA}^{2}+\overline{MB}^{2}=2\overline{MI}^{2}+\dfrac{\overline{AB}^{2}}{2}$
b) $\overline{MA}.\overline{MB}=\overline{MI}^{2}-\dfrac{\overline{AB}^{2}}{4}$
Exercice 4
Une droite est munie d'un repère $(O\;,\ \vec{i})$. On place les points $A\;,\ B\;,\ C\;,\ D$ de cette droite d'abscisses respectives $4\;,\ \dfrac{15}{2}\;,\ -1$ et $-\dfrac{11}{3}.$
1) Calculer $\overline{AB}\;,\ \overline{BC}\;,\ \overline{AD}\;,\ \overline{CA}.$
2) Déterminer l'abscisse $x$ des points $M$ dans chacun des cas suivants :
a) $\overline{AM}=3$
b) $2\overline{CM}+\overline{MA}=1$
c) $2\overline{OB}=3\overline{AM}$
d) $0\leq\overline{CM}\leq 2$
e) $3\overline{AM}=\overline{AC}$
f) $AM^{2}=4$
Exercice 5
Sur un axe $(D)$, on considère deux points $A$ et $B$ d'abscisses respectives -1 et 2.
1) Placer le point $C$ tel que $\overline{CA}=2\overline{CB}.$
2) Montrer qu'il existe un point $M$ tel que : $\overline{MA}+2\overline{MB}=0.$
3) Quels sont les points $M$ de $(D)$ tels que $MA^{2}-4MB^{2}=0\ ?$
Exercice 6
Soient $A\;,\ B\;,\ C$ et $D$ quatre points d'une même droite $(\Delta)$ muni d'un repère $(O\;,\ I ).$
1) a) Établir, à l'aide des abscisses des points la relation suivante : $$\overline{DA}.\overline{BC}+\overline{DB}.\overline{CA}+\overline{DC}.\overline{AB}=0\quad\text{(relation dite d'Euler)}$$
2) Établir, en utilisant la relation de Chasles, la relation d'Euler.
3) Former l'expression $\overline{DA}^{2}.\overline{BC}+\overline{DB}^{2}.\overline{CA}$ et en déduire la relation suivante : $$\overline{DA}^{2}.\overline{BC}+\overline{DB}^{2}.\overline{CA}+\overline{DC}^{2}.\overline{AB}+\overline{BC}.\overline{CA}.\overline{AB}=0\quad\text{(relation dite de Stewart)}$$
Exercice 7 Applications du théorème de Thalès et de sa réciproque
Les différentes questions sont complètement indépendantes.
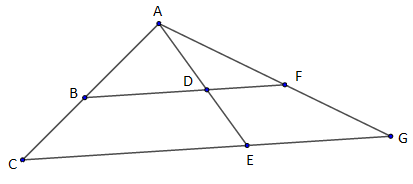
1) $ACG$ est un triangle. $B$ est un point du segment $[AC]\;,\ E$ un point du segment $[CG].$ La parallèle à $(CG)$ passant par $B$ coupe $(AE)$ en $D$ et $(AG)$ en $F.$
Montrer que : $\dfrac{\overline{EG}}{\overline{DF}}=\dfrac{\overline{CE}}{\overline{BD}}$
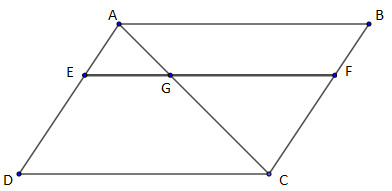
2) $ABCD$ est un parallélogramme. $E$ est un point du segment $[AD].$ La parallèle à $(AB)$ passant par $E$ coupe $(AC)$ en $G$ et $(BC)$ en $F.$
Montrer que : $\dfrac{\overline{EG}}{\overline{AB}}=\dfrac{\overline{BF}}{\overline{BC}}$
3) $RST$ est un triangle. $L$ appartient à $[RS]$ et $M$ appartient à $[RT].$
Indiquer si $(LM)$ est parallèle à $(ST)$ dans chacun des cas suivants :
$RS=7\;;\quad RT=14\;;\quad RL=1.5\;;\quad RM=3$
$RS=8\;;\quad RT=9\;;\quad RL=5\;;\quad RM=5.5$
$RS=7\;;\quad RT=9\;;\quad SL=3\;;\quad RM=5$
$RS=12\;;\quad RT=18\;;\quad SL=18\;;\quad MT=4.5$
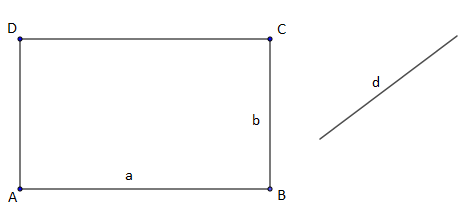
4) Soit $ABCD$ un rectangle donné de cotés $a$ et $b.$ Construire exactement un rectangle de même aire et dont un côté a pour longueur $d\ (d$ longueur donnée).
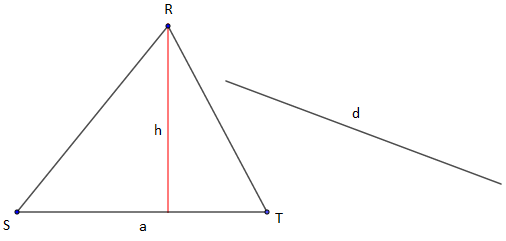
5) Soit $RST$ un triangle donné de cotés $a=ST$ donné et de hauteur $h.$ Construire un rectangle de même aire et dont un côté a pour longueur $d\ (d$ longueur donnée).
6) Placer exactement les points $L\;,\ M\;,\ N$ d'abscisses respectives $\dfrac{2}{3}\;,\ \dfrac{5}{7}\;,\ \dfrac{4}{11}$ sur la droite $(D)$ de repère $(A\;,\ B).$
7) Placer exactement les points $S\;,\ T\;,\ U$ d'abscisses respectives $-\dfrac{1}{3}\;,\ -\dfrac{3}{7}\;,\ -\dfrac{7}{11}$ sur la droite $(D)$ de repère $(A\;,\ B).$
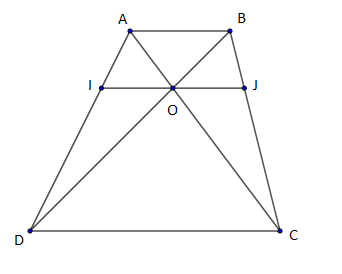
8) $ABCD$ est un trapèze. Les diagonales $(AC)$ et $(BD)$ se coupent en $O.$ Par $O$, on trace une parallèle à $(AB)$ qui coupe $(AD)$ en $I$ et $(BC)$ en $J.$
Démontrer que $\dfrac{\overline{IO}}{\overline{AB}}=\dfrac{\overline{OJ}}{\overline{AB}}$. Que peut-on en déduire pour $I\;,\ O$ et $J\ ?$
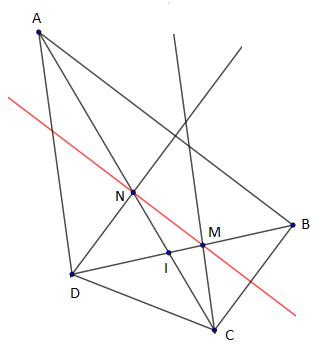
9) $ABCD$ est un quadrilatère. La parallèle à $(AD)$ passant par $C$ coupe $(BD)$ en $M.$ La parallèle à $(BC)$ passant par $D$ coupe $(AC)$ en $N.$
On appelle I le point de rencontre de $(AC)$ et $(BD).$
Calculer $\dfrac{\overline{IN}}{\overline{IC}}$ et $\dfrac{\overline{IM}}{\overline{ID}}$.
Démontrer que $(MN)$ est une droite parallèle à $(AB).$
Repères et droites du plan
Exercice 8
Soit $ABCD$ un parallélogramme non aplati.
On pose $\vec{u}=\overrightarrow{AB}$ et $\vec{v}=\overrightarrow{AC}$
1) Les vecteurs $\vec{u}+\vec{u}$ et $\vec{u}-\vec{v}$ sont-ils colinéaires ?
2) On pose $\vec{i}=\vec{u}+\vec{u}$ et $\vec{j}=\vec{u}-\vec{v}$
Donner les coordonnées de $\vec{u}$ et $\vec{v}$ dans la base $(\vec{i}\;,\ \vec{j}).$
3) Donner les coordonnées de $A\;,\ B\;,\ C$ et $D$ dans le repère $(B\;,\ \vec{i}\;,\ \vec{j}).$
4) Existe-t-il des points qui ont les mêmes coordonnées relativement aux repères $(A\;,\ \vec{u}\;,\ \vec{v})$ et $(B\;,\ \vec{i}\;,\ \vec{j}).\ ?$
Exercice 9
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs dont les coordonnées relativement à la base $(\vec{i}\;,\ \vec{j})$ sont respectivement $(1\;,\ 2)$ et $(-1\;,\ -3).$
1) Montrer que $(\vec{u}\;,\ \vec{v})$ est une base de l'ensemble des vecteurs du plan.
2) Exprimer $\vec{i}$ et $\vec{j}$ à l'aide de $\vec{u}$ et $\vec{v}.$
3) Soit $\vec{w}_{1}\;,\ \vec{w}_{2}$ et $\vec{w}_{3}$, trois vecteurs dont les coordonnées dans $(\vec{i}\;,\ \vec{j})$ sont respectivement $(1\;,\ 2)\;,\ (6\;,\ -4)$ et $(-3\;,\ 2).$
Quelles sont les coordonnées de $\vec{w}_{1}\;,\ \vec{w}_{2}$ et $\vec{w}_{3}$ dans $(\vec{u}\;,\ \vec{v})\ ?$
4) Calculer les déterminants des couples de vecteurs suivants dans la base $(\vec{i}\;,\ \vec{j})$, puis dans la base $(\vec{u}\;,\ \vec{v})\;,\ (\vec{w}_{1}\;,\ \vec{w}_{2})\;,\ (\vec{w}_{2}\;,\ \vec{w}_{3})$ et $(\vec{w}_{1}\;,\ \vec{w}_{3})$
Exercice 10 Repérer un point - Placer un point
Le plan est muni d'un repère orthonormé $(O\;;\ I\;;\ J)$ dessiné ci-dessous :
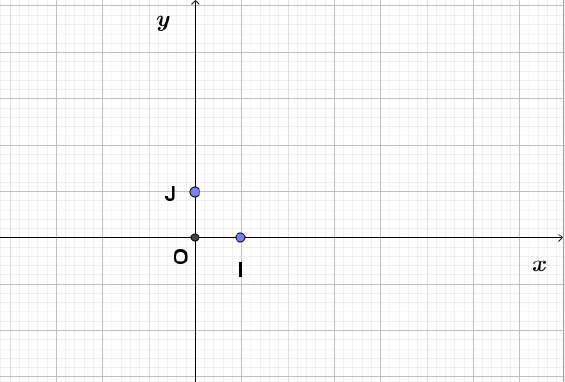
1) Placer les points $A(-3\;;\ 0)\;,\ B(0\;;\ -2)$ et $C(-3\;;\ -2).$
2) a) On note $A'$ le symétrique de $A$ par rapport au point $O$ et $B'$ le symétrique de $B$ par rapport à $O.$
Placer les points $A'$ et $B'$ puis préciser leurs coordonnées.
b) On note $C'$ le point tel que le quadrilatère $OA'C'B'$ soit un rectangle.
Préciser les coordonnées du point $C'.$
3) a) Préciser pourquoi $(O\;;\ A\;;\ B)$ constitue un nouveau repère du plan. Est-il orthogonal ou orthonormé ?
b) Déterminer les coordonnées de chacun des points $O\;,\ A\;,\ B\;,\ C\;,\ A'\;,\ B'$ et $C'$ dans ce repère $(O\;;\ A\;;\ B).$
Exercice 11 Lire des coordonnées
$ABCD$ est un carré. $E$ est le milieu du segment $[AB]$ et $F$ est le milieu du segment $[BD].$
Dans le repère orthonormé $(A\;;\ B\;;\ D)$, préciser les coordonnées des différents points de la figure.
Exercice 12 Coordonnées du milieu d'un segment
Dans un repère, on donne les points $R(4\;;\ -1)\;,\ S(2\;;\ 5)\;,\ T(3\;;\ 2)$ et $U(5\;;\ 2).$
1) Placer les points $R\;,\ S\;,\ T$ et $U$ dans ce repère.
2) Démontrer que le point $T$ est le milieu du segment $[RS].$
3) a) Tracer la parallèle à la droite $(RU)$ passant par le point $T.$ Justifier pourquoi elle coupe le segment $[SU]$ en son milieu $V.$
b) Calculer les coordonnées du point $V.$
Exercice 13 Démontrer qu'un quadrilatère est un parallélogramme
Dans un repère, on donne les points $D(-2\;;\ 1)\;,\ E(3\;;\ 3)\;,\ F(1\;;\ -1)$ et $G(-4\;;\ -3).$
Démontrer que le quadrilatère $DEFG$ est un parallélogramme.
Exercice 14
Soit $ABC$ un triangle et $\alpha$ un réel. On définit trois points $P\;,\ Q\;,\ R$ par : $$\overrightarrow{CR}=-\alpha\overrightarrow{CB}\quad\overrightarrow{CQ}=\alpha\overrightarrow{CA}\quad\text{et}\quad\overrightarrow{AP}=\alpha\overrightarrow{AB}$$
1) Faire une figure pour $\alpha=-2.$
2) Déterminer dans le repère $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC})$ les coordonnées des points $P\;,\ Q$ et $R$ en fonction de $\alpha.$
3) Exprimer dans la base $(\overrightarrow{AB}\;,\ \overrightarrow{AC})$ les coordonnées des vecteurs $\overrightarrow{PQ}$ et $\overrightarrow{PR}$ à l'aide de $\alpha.$
4) Déterminer $\alpha$ pour que $P\;,\ Q\;,\ R$ soient alignés et distincts.
5) Faire la figure dans ce cas et montrer que $Q$ est alors le milieu de $[PR].$
Exercice 15
Dans chacun des cas suivants, on demande :
de donner une représentation paramétrique de la droite $(D).$
de déterminer les points d'intersection de $(D)$ avec les axes.
de tracer $(D).$
1) $(D)$ passe par $A(1\;,\ 2)$ et $B(-2\;,\ 4).$
2) $(D)$ passe par $A(1\;,\ 2)$ et a pour vecteur directeur $\vec{u}(3\;,\ 1).$
3) $(D)$ passe par $A(1\;,\ 2)$ et a pour coefficient directeur -2.
4) $(D)$ a pour équation : $x+2y-3=0.$
Exercice 16
Soit $(D)$ la droite d'équation $3x-2y+2=0$ et $(D')$ la droite de représentation paramétrique $\left\lbrace\begin{array}{rcl} x&=&3-4t \\ y&=&-1+2t\end{array}\right.$
1) Pour chacune des droites, donner deux vecteurs directeurs .
2) Les points suivants appartiennent-ils à $(D)$ ou $(D')$ :
$A(2\;,\ 4)\;,\ B(3\;,\ -1)\;,\ C(-1\;,\ 1)$ et $D(4\;,\ 7)\ ?$
Exercice 17
Le plan est rapporté à un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$
On considère l'ensemble $(D_{m})$ des points $M$ du plan dont les coordonnées $(x\;,\ y)$ vérifient l'équation : $$(2m-1)x+(3-m)y-7m+6=0$$
1) Montrer que, quel que soit $m\in\mathbb{R}\;,\ (D_{m})$ est une droite .
2) Dans chacun des cas suivants, trouver m pour que :
a) $(D_{m})$ passe par $A(1\;,\ 1).$
b) $(D_{m})$ passe par l'origine du repère.
c) $(D_{m})$ soit parallèle à l'axe des abscisses.
d) $(D_{m})$ soit parallèle à l'axe des ordonnées.
e) $(D_{m})$ ait pour coefficient directeur -1.
f) $(D_{m})$ soit parallèle à la droite d'équation $x-3y-5=0.$
3) Existe-t-il un point commun à toutes les droites $(D_{m})\ ?$
Exercice 18
Soit un parallélogramme $ABCD$ de centre $O$
1) On choisit $(\overrightarrow{AB}\;,\ \overrightarrow{AD})$ comme base de vecteurs. Pourquoi ce choix est-il possible ?
2) Quelles sont les coordonnées des vecteurs $\overrightarrow{AC}\;,\ \overrightarrow{AO}$ et $\overrightarrow{DB}$ (justifiez) ?
3) Construire $E$ tel que les coordonnées de $\overrightarrow{CE}$ soient $\left(\dfrac{2}{3}\;;\ -\dfrac{5}{3}\right)$
4) Démontrer que $D\;,\ B$ et $E$ sont alignés.
Exercice 19
1) Parmi ces droites, lesquelles sont parallèles, confondues ou sécantes ?
$(D_{1})\ :\ 6x-3y+4=0\quad (D_{2})\ :\ 2x-y+7=0\quad (D_{3})\ :\ y=2x+\dfrac{4}{3}$
$(D_{4})\ :\ -12x+6y-8=0\quad(D_{5})\ :\ 5x+2y+10=0\quad (D_{6})\ :\ x-5y-10=0$
$(D_{7})\ :\ 3x-2y+5=0\quad (D_{8})\ :\ 2x+3y=5$
2) Déterminer les coordonnées du point d'intersection de $D_{7}$ et $D_{2}$
Exercice 20
Tracer les droites d'équation :
$(\Delta_{1})\ :\ y=2x-4\quad (\Delta_{2})\ :\ y=-3x+5$
$\quad$
$ (\Delta_{3})\ :\ y=\dfrac{3}{2}x-4$
$\quad$
$ (\Delta_{3})\ :\ y=\dfrac{3}{2}x-4$
$(\Delta_{4})\ :\ y=-\dfrac{2}{5}x+\dfrac{1}{5}\quad(\Delta_{5})\ :\ x+2y-2=0$
$\quad$
$(\Delta_{6})\ :\ 2x-\dfrac{1}{4}y+1=0$
$\quad$
$(\Delta_{6})\ :\ 2x-\dfrac{1}{4}y+1=0$
$(\Delta_{7})\ :\ 5x+2y-3=0$
$\quad$
$ (\Delta_{8})\ :\ -3x+2y-7=0$
$\quad$
$ (\Delta_{8})\ :\ -3x+2y-7=0$
Exercice 21
Soient $ABC$ un triangle et $O$ un point de la droite $(BC)$ tel que $O\neq B$ et $O\neq C.$ Par $B$ et $C$, on trace deux droites $\Delta_{1}$ et $\Delta_{2}$ parallèles. La parallèle à $(AC)$ passant par $O$ coupe $\Delta_{1}$ en $I$ et la parallèle à $(AB)$ passant par $O$ coupe $\Delta_{2}$ en $J.$
Le but du problème est de montrer que $A\;,\ I\;,\ J$ sont alignés.
On choisit le repère $\mathcal{R}=(O\;,\ \overrightarrow{OI}\;,\ \overrightarrow{OJ}).$
1) Faire une figure soignée.
2) Soient $(\alpha\;,\ \beta)$ les coordonnées de $B$ dans le repère $\mathcal{R}.$ Déterminer les coordonnées de $\overrightarrow{JB}.$
3) Déterminer les coefficients directeurs des droites $(OB)\;,\ (BJ)$ et $(CJ).$
4) Déterminer les équations réduites des droites $(BC)$ et $(CJ)$ et en déduire l'abscisse de $C.$
5) Quelles sont les coordonnées du point $A$ ?
6) Prouver que $A\;,\ I$ et $J$ sont alignés.
Exercice 22
$ABCD$ est un parallélogramme, $a$ et $b$ sont deux réels non nuls. $E$ et $F$ sont les points tels que : $$\overrightarrow{AE}=a\overrightarrow{AB}\quad\text{et}\quad\overrightarrow{AF}=b\overrightarrow{AD}$$
La droite parallèle à $(AD)$ passant par $E$ coupe $(CD)$ en $G$ et la droite parallèle à $(AB)$ passant par $F$ coupe $(BC)$ en $H.$ On note $K$ le point d'intersection des droites $(EG)$ et $(FH).$
On considère le repère $\mathcal{R}=(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD}).$
N.B. On fera une figure illustrant les données avec $a=\dfrac{3}{2}\;;\ b=2\;;\ AB=4\;cm$ et $AD=2.5\;cm.$
1) Déterminer les coordonnées des points $A\;,\ B\;,\ C\;,\ D\;,\ E\;,\ F\;,\ G\;,\ H$ et $K$ dans le repère $R.$
2) Déterminer une condition sur $a$ et $b$ pour que les droites $(FG)$ et $(EH)$ soient parallèles, puis montrer qu'avec cette condition, on a : $(FG)//(AC)$ et $(EH)//(AC).$
3) Montrer que si $a+b=1$, alors $K\in(BD).$
4) Déterminer une condition sur $a$ et $b$ pour que les droites $(EF)$ et $(GH)$ soient parallèles, puis montrer que, dans ce cas, on a : $(EF)//(DB)$ et $(GH)//(DB).$
5) Montrer alors que $K\in(AC).$
6) Montrer que le quadrilatère $EFGH$ est un parallélogramme si, et seulement si : $\left\lbrace\begin{array}{rcl} a+b&=&1 \\ a&=&b\end{array}\right.$
7) Montrer qu'alors $E$ et $G$ sont les milieux respectifs de $[AB]$ et $[CD]$ et que les parallélogrammes $ABCD$ et $EFGH$ ont même centre.
Exercice 23
Dans le plan rapporté à un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ soient le point $A(-2\;;\ 1)$ et le vecteur $\vec{u}=\begin{pmatrix} -2 \\ 3\end{pmatrix}$. On note $d$ la droite passant par $A$ et de vecteur directeur $\vec{u}.$
1) Le point $O$ appartient-il à $d$ ? Le point $B(-1\;;\ -1/2)\ ?$
2) Donner une équation de $d$ et la tracer. Quelles sont les coordonnées de ses points d'intersection avec les axes ?
3) $C$ est le point tel que $\overrightarrow{BC}=2\overrightarrow{AO}.$ Déterminer les coordonnées de $C$ ainsi qu'une équation de la droite $(BC).$ La tracer et déterminer son intersection avec $d.$
4) Soit $d'$ la droite passant par $D(0\;;\ 4)$ et parallèle à $d.$ Donner une équation de $d'$, la tracer et déterminer graphiquement puis par le calcul les coordonnées de son point d'intersection $K$ avec $(BC).$
5) Soit $\delta$ la droite d'équation $x+2y-4=0.$ Déterminer son vecteur directeur ainsi que deux de ses points. Tracer $\delta.$ Que peut on en dire ? Déterminer ses points d'intersection avec $d$ et $d'.$
6) Montrer de trois manières différentes que la figure formée par $d\;,\ d'\;,\ \delta$ et $(BC)$ est un parallélogramme.
Exercice 24
Soient $A\begin{pmatrix} 2\\ 5\end{pmatrix}\;,\ $ $B\begin{pmatrix} 3\\ -4\end{pmatrix}\ $ et $C\begin{pmatrix} 1\\ 7\end{pmatrix}$ trois points du plan.
1) Déterminer les équations cartésiennes de :
a) la droite $(AB)$
b) la droite $\mathfrak{D}$ passant par $C$ et parallèle à $(AB)$
c) la médiatrice de $[AC]$
d) la hauteur issue de $C$
2) Déterminer $d(C\;,\ (AB)\;)\ $ et $d(B\;,\ \mathfrak{D})$, les distances entre $C$ et $(AB)$ et, $B$ et $\mathfrak{D}$ respectivement.
3) Déterminer l'équation du cercle de diamètre $[BC]$
Exercice 25
Soit $(\mathfrak{D}_{m})$ la droite d'équation : $(m-1)x+(m-2)y+m=0$
1) Montrer que $(m-1\;;\ m-2)\neq (0\;;\ 0)$
2)a) Déterminer $m$ pour que $(\mathfrak{D}_{m})\parallel$ à l'axe des abscisses.
b) Déterminer $m$ pour que $(\mathfrak{D}_{m})\parallel$ à l'axe des ordonnées.
c) Déterminer $m$ pour que $(\mathfrak{D}_{m})\parallel\ \mathfrak{D}\ :\ x+3y+2=0$
Exercice 26
Soit $(\Delta_{m})$ la droite d'équation : $(2m-1)x+(3-m)y-7m+6=0$
1) Pour quelles valeurs de $m\;,\ \Delta_{m}$ est-elle :
a) parallèle à $(Ox)$ ?
b) parallèle à $(Oy)$ ?
c) parallèle à $\Delta\ :\ 2x+y-4=0$ ?
d) perpendiculaire à $\Delta'\ :\ x+y=0$ ?
2) Montrer que toutes les droites $(\Delta_{m})$ passent par un point fixe $A$ dont on déterminera les coordonnées.
Exercice 27
1) Soit la droite $(\Delta)\ :\ 3x+2y-5=0$
Déterminer un système d'équations paramétriques de $(\Delta)$
2) Soit $(\Delta')$ la droite dont un système d'équations paramétriques est
$$\left\lbrace\begin{array}{lcl} x&=&3t+1\\ y&=&-2t+3 \end{array}\right.$$
Déterminer une équation cartésienne de $(\Delta')$
Exercice 28
Soient $A\begin{pmatrix} 1\\ 2 \end{pmatrix}\ $ et $B\begin{pmatrix} 3\\ 4\end{pmatrix}$ deux points du plan, $\mathfrak{D}_{1}\ :\ 2x-3y+5=0$
1) déterminer un système d'équations paramétriques des droites $(AB)$ et $\mathfrak{D}_{1}$
2) Soit $\mathfrak{D}_{2}\ :\ \left\lbrace\begin{array}{lcl} x&=&2-t\\ y&=&3+4t \end{array}\right.$
a) $A\begin{pmatrix} 1\\ 2 \end{pmatrix}\ $ et $D\begin{pmatrix} 0\\ 11 \end{pmatrix}$ appartiennent-ils à $\mathfrak{D}_{2}$ ?
b) Déterminer l'équation cartésienne de $\mathfrak{D}_{2}$
c) Déterminer $d(A\;,\ \mathfrak{D}_{2})$ ; la distance entre le point $A$ et la droite $\mathfrak{D}_{2}$
3) Déterminer les coordonnées des points d'intersection de :
a) $\mathfrak{D}_{1}$ et $\mathfrak{D}_{2}$
b) $\mathfrak{D}_{1}\ $ et $\mathfrak{D}_{6}\ :\ x+y+1=0$
c) $\mathfrak{D}_{2}\ $ et $\mathfrak{D}_{7}\ :\ \left\lbrace\begin{array}{lcl} x&=&1+t\\ y&=&7-2t \end{array}\right.$
Équations de cercle
Exercice 29
1) Les équations suivantes sont-elles des équations de cercle ?
Si oui, donner le centre et le rayon.
a) $x^{2}+y^{2}-6x+8y-5=0$
b) $x^{2}+y^{2}+2x+4y-1=0$
2) Discuter suivant les valeurs du paramètre $m$ la nature et les éléments caractéristiques de l'ensemble $(\mathcal{E})$ des points $M\begin{pmatrix} x\\ y \end{pmatrix}$ tels que $$x^{2}-2x+y^{2}+4x=m^{2}-6$$
Exercice 30
Soit $(O\;;\ \vec{i}\;,\ \vec{j})$ un repère du plan, $A\begin{pmatrix} 2\\ 1 \end{pmatrix}\;,\ B\begin{pmatrix} 3\\ 4 \end{pmatrix}\;,\ C\begin{pmatrix} 1\\ 1 \end{pmatrix}$ et $\Omega\begin{pmatrix} 3\\ 2 \end{pmatrix}$ quatre points dans $(O\;;\ \vec{i}\;,\ \vec{j}).$
1) Trouver les coordonnées de $A\;,\ B$ et $C$ dans $(\Omega\;;\ \vec{i}\;,\ \vec{j})$ et dans $(\Omega\;;\ 2\vec{i}\;,\ 3\vec{j}).$
2) Déterminer une équation cartésienne de la médiane issue de $A$, dans $(\Omega\;;\ \vec{i}\;,\ \vec{j}).$
Exercice 31
Le plan est muni d'un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j}).$
1) Déterminer l'équation cartésienne d'un cercle de centre $\Omega(-2\;;\ 4)$ et de rayon 2.
2) Soit $$(E)\ :\ x^{2}+y^{2}-6x+4y-3=0$$ Montrer que $(E)$ est l'équation d'un cercle dont on déterminera le centre $I$ et le rayon $r.$
Exercice 32
Soient $(\mathcal{C})$ et $(\mathcal{C}')$ deux cercles d'équations respectives $$x^{2}+y^{2}-2x+4y-20=0$$$$\text{ et}\quad x^{2}+y^{2}+2x-6y-26=0$$
1) $(\mathcal{C})$ et $(\mathcal{C}')$ sont-ils sécants ?
2) Si oui, déterminer les coordonnées de leurs points d'intersection.

Commentaires
Mamadou Dia (non vérifié)
lun, 07/22/2019 - 09:47
Permalien
Bj, chers monsieurs ou
Fat Bintou Diop (non vérifié)
jeu, 05/05/2022 - 21:20
Permalien
Reste de la correction
Dior Kama (non vérifié)
lun, 03/02/2020 - 22:51
Permalien
la correction
Amadou sow (non vérifié)
jeu, 04/23/2020 - 02:20
Permalien
Et si on aurait les
Alssainy Diallo (non vérifié)
sam, 08/22/2020 - 01:07
Permalien
Je voulais vérifie de ce que je fais est bon
Anonyme (non vérifié)
mar, 09/15/2020 - 15:45
Permalien
J'aimerais avoir la
Boniface mané (non vérifié)
mar, 03/21/2023 - 14:47
Permalien
Explication
Anonyme (non vérifié)
dim, 04/04/2021 - 20:34
Permalien
$\frac{1}{2}=\overline{AB}$
Fatoumata (non vérifié)
mer, 06/08/2022 - 23:01
Permalien
Avis
Ajouter un commentaire