Série d'exercices : Équation du premier degré à une inconnue 4e
Classe:
Quatrième
Exercice 1 Vocabulaire
Recopier puis compléter parles mots qui conviennent.
1) Une $\ldots\ldots$ est une $\ldots\ldots$ dans la quelle un nombre est inconnu.
2) $\ldots\ldots$ l'équation, c'est trouver toutes les valeurs de $\ldots\ldots$ pour lesquelles $\ldots\ldots$ est vérifiée.
3) Les $\ldots\ldots$ de $\ldots\ldots$ sont les nombres qui vérifient l'$\ldots\ldots$
4) On ne change pas les $\ldots\ldots$ d'une $\ldots\ldots$ lorsqu'on ajoute le même nombre dans chaque $\ldots\ldots$
5) Dans l'équation : $2x-4=7\;;\quad 2x-4$ est le $\ldots\ldots$ de gauche et 7 est le $\ldots\ldots$ de $\ldots\ldots$
Exercice 2 "Équation de la forme $x+a=b$"
Résoudre dans $\mathbb{Q}$ chacune des équations suivantes en utilisant les propriétés des inégalités.
a) $x+3=6\qquad$ b) $x+5=-6\qquad$ c) $x+3=-8$
d) $x-4=2\qquad$ e) $x-1=-4\qquad$ f) $-4+x=-4$
g) $x-\dfrac{2}{5}=\dfrac{4}{3}\qquad$ h) $x+\dfrac{1}{3}=\dfrac{3}{2}\qquad$ i) $x-\dfrac{4}{5}=-\dfrac{1}{3}$
j) $-\dfrac{2}{5}+x=\dfrac{1}{2}\qquad$ l) $x-\dfrac{4}{5}=\dfrac{1}{3}\qquad$ m) $-x+\dfrac{1}{5}=-\dfrac{1}{3}$
Exercice 3 "Équation de la forme $ax=b$"
Résoudre dans $\mathbb{Q}$ chacune des équations suivantes en utilisant les propriétés des inégalités.
a) $4x=3\qquad$ b) $-2x=4.8\qquad$ c) $3x=-19$
d) $2x=\dfrac{3}{7}\qquad$ e) $-2x=-\dfrac{7}{3}\qquad$ f) $\dfrac{4}{3}x=-\dfrac{9}{8}$
Exercice 4 "Équation de la forme $ax+b=c$"
a) $-2x-1=5\qquad$ b) $-4x+2=5\qquad$ c) $-6x-1=-7$
d) $-\dfrac{3}{4}x-1=2\qquad$ e) $\dfrac{6}{5}x-\dfrac{1}{3}=3\qquad$ f) $-2x+\dfrac{1}{4}=\dfrac{1}{3}$
Exercice 5 "Équation de la forme $ax+b=cx+d$"
Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $2x+3=4x+5\qquad$ b) $2x-3=-4x+5$
c) $-2x+3.5=4x-5\qquad$ d) $-2x-3=-4x+5$
e) $3-4x+3=5-6x\qquad$ f) $-3-4x=-1.5-7x$
g) $3x-4=8.3\qquad$ h) $-5x+7=6\qquad$ i) $2x-2=2x$
Exercice 6 "Approfondissement"
Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $4(1-3x)=-3(2-x)\qquad$ b) $(3x-1)-(x-1)=3x-5$
c) $6(2x-1)-2(-2x+3)=0\qquad$ d) $2(x-1)-3(-4x+7)=0$
e) $-2(1-3x)=-3(2-x)\qquad$ f) $-3(1-3x)=2(2-x)+5$
g) $3x-6(3-4x)=9x-2\qquad$ h) $3x-2(x^{2}-1)=-2x^{2}-2$
3) Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $-\dfrac{8}{7}x+2=1\qquad$ b) $\dfrac{8}{7}x-8=1-x$
c) $\dfrac{3}{4}x-2x=-3+x\qquad$ d) $\dfrac{2}{3}(5x-1)=\dfrac{3}{4}(x-3)$
Exercice 7 "Équation produit"
1) Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $(x-4)(x+5)=0\qquad$ b) $\left(x+\dfrac{5}{3}\right)\left(x-\dfrac{3}{4}\right)=0$
c) $(2x-1)(3x+4)=0\qquad$ d) $\left(3x-\dfrac{3}{4}\right)\left(2x-\dfrac{1}{3}\right)=0$
2) Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $x^{2}-6x+9=0\qquad$ b) $49x^{2}-1=0$
c) $4x^{2}+12x+9=0\qquad$ d) $36x^{2}-1=0$
e) $x^{2}-1=0\qquad$ F) $4x^{2}-49=0$
3) Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $(2x-1)(4x-3)-(2x-1)(6x-1)=0$
b) $4x^{2}-1+(2x-1)(4x-5)=0$
c) $(3x-1)^{2}-(x-3)^{2}=0$
Exercice 8 "Équation de la forme $\dfrac{ax+b}{k}=\dfrac{cx+d}{k'}$"
Résoudre dans $\mathbb{Q}$ chacune des équations suivantes
a) $\dfrac{x+1}{2}=\dfrac{2x-1}{3}\qquad$ b) $\dfrac{x-1}{3}=\dfrac{7x-2}{5}$
c) $\dfrac{4x-5}{3}+\dfrac{7x-2}{2}=0\qquad$ d) $\dfrac{6x-1}{4}=-\dfrac{5x-1}{3}$
Exercice 9 "Équation et problème"
Ndeuss a $15$ ans ; sa petite sœur Coumba a $6$ ans.
Dans combien d'année l'âge de Neuss sera le double de sa sœur Coumba.
Exercice 10 "Équation et problème"
Adama, Assane et Abdou se partagent $79$ billes, Assane en a $2$ fois plus que Adama et Abdou en a $7$ de plus que Adama. Combien Adama, Assane et Abdou ont-ils de billes ?
Exercice 11 "Mise en équation"
Traduire chacune des phrases suivantes par une équation.
1) La somme d'un nombre et de $7$ est égale à $5.$
2) La différence d'un nombre et de $8$ est égale à $-3.$
3) Le produit d'un nombre et de $10$ est égal à $11.$
4) Le quotient d'un nombre et de $4$ est égal à $5.$
Exercice 12 "Mise en équation"
1) Imaginer une équation du premier degré à une inconnue ayant pour solution $x=3.$
2) Imaginer une équation du premier degré à une inconnue ayant pour solution $t=-2.$
Exercice 13 "Équation et problème"
Khoudia dépense le quart de son salaire pour son logement et les deux cinquièmes pour la nourriture.
Il lui reste $227\,500\;F$ pour les autres dépenses.
Calculer son salaire mensuel.
Exercice 14 Problème
On donne $f(x)=4x^{2}-1-(1-2x)(3x+4).$
1) a) Développer, réduire et ordonner $f(x).$
b) Calculer $f(0).$
2) a) Factoriser $f(x).$
b) Résoudre dans $\mathbb{Q}$ l'équation $f(x)=0$
Exercice 15 Problème
On considère les expressions suivantes :
$f(x)=(5x-2)^{2}-(2x+3)^{2}\;;\quad g(x)=(3x-5)(2x-1)+9x^{2}-30x+25.$
1) Développer, réduire et ordonner $f(x)$ et $g(x).$
2) Factoriser $f(x)$ et $g(x)$ en déduire le facteur commun de $f(x)$ et $g(x).$
3) Résoudre dans $\mathbb{Q}$ les équations suivantes :
$f(x)=0\ $ et $\ g(x)=0.$
4) Résoudre dans $\mathbb{Q}$ les équations suivantes :
$f(x)=21x^{2}\ $ et $\ g(x)=15x^{2}.$
Exercice 16 Problème et Identités remarquables
On considère les expressions suivantes.
$A(x)=(2x-1)^{2}+2(2x-1)(7x-1)+(7x-1)^{2}.$
$B(x)=(x-1)^{2}-2(x-1)(3x-1)+(3x-1)^{2}.$
$C(x)=x^{2}+2x(8x-1)+(8x-1)^{2}.$
1) Développer, réduire et ordonner les expressions suivantes : $A(x)\;;\ B(x)$ et $C(x).$
2) Factoriser les expressions : $A(x)\;;\ B(x)$ et $C(x).$
3) Résoudre dans $\mathbb{Q}$ les équations suivantes :
$A(x)=0\;;\quad B(x)=0\ $ et $\ C(x)=81x^{2}.$
Exercice 17 Problème
Le rectangle ci-dessous a pour longueur $AC=7\;cm$ et pour largeur $CD=4\;cm.\ B\in[AC]$ tel que $BC=x\;;\ F\in[AE]$ tel que $FE=x.$
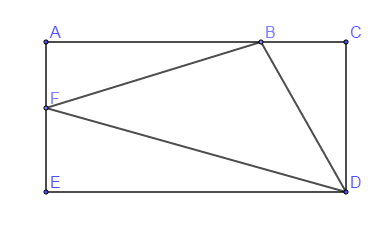
1) Calculer l'aire du rectangle $ACDE.$
2) Calculer les aires des triangles $BCD$ et $DEF$ en fonction de $x.$
3) Montrer que l'aire du triangle $ABF$ est de : $$0.5x^{2}-5.5x+14$$
4) En déduire que l'aire de $FBD$ est égale à $-0.5x^{2}+14$
5) Déterminer pour quelle valeur de $x$ l'aire du triangle $FBD$ représente les $\dfrac{3}{7}$ de l'aire du rectangle $ACDE.$
Exercice 18 Équation et valeur absolue ( hp)
Résoudre dans $\mathbb{Q}$ chacune des équations suivantes.
a) $|2x-3|=|4x+1|\;;\qquad$ b) $|-4x-1|=6$
c) $\left|3x-\dfrac{4}{3}\right|=|-2x|\;;\qquad$ d) $|2x-1|=2\pi$
Exercice 19
Résous dans $\mathbb{Q}$ les équations ci-dessous
$5n-\dfrac{3}{2}=n+\dfrac{1}{6}$ ;
$\dfrac{3m}{7}+2=5-\dfrac{m}{14}$ ;
$-\dfrac{5}{3}+7x+1=\dfrac{x}{2}-1$ ;
$\dfrac{2}{5}\left(\dfrac{2}{5}x+5\right)=-\dfrac{1}{2}\left(1-\dfrac{9}{5}x\right).$
Exercice 20
Résous dans $\mathbb{Q}$ les équations ci-dessous
$\dfrac{n}{2}-\dfrac{1}{3}\left(\dfrac{1}{2}-n\right)=\dfrac{7}{6}n+\dfrac{2}{3}$ ;
$2t-\dfrac{1}{4}=\dfrac{t}{2}$ ;
$\dfrac{m}{3}=m-10$ ;
$3x=\dfrac{x}{3}+8$ ;
Exercice 21
Ngor et Diégane ont ensemble $48$ billes, soit $x$ le nombre de billes de Ngor
1) Exprime en fonction de $x$, le nombre de billes de Diégane
2) Détermine $x$ sachant que Ngor a $2$ fois plus de billes que Diégane.
Exercice 22
Un père a $24$ ans de plus que son fils, calcule l'âge de chacun quand ils auront ensemble $100$ ans.
Exercice 23
Les dimensions d'un rectangle sont $3\;m\text{ et }4\;m$, quel nombre faut-il ajouter à la longueur et à la largeur pour que le périmètre double ?
Exercice 24
Une mère a $15$ ans de plus que sa fille, dans $10$ ans l'âge de la mère sera le double de l'âge de la fille ;
quel est l'âge de la mère et celui de la fille ?
Exercice 25
Nafi a eu $13$ et $15$ aux $2$ premiers contrôles de Maths ; quelle note doit-elle obtenir au $3^{ème}$ contrôle pour que sa moyenne soit $16$ ?
Exercice 26
Un terrain rectangulaire a un périmètre de $4.5\;km$ ; la longueur mesure $350\;m$ de plus que la largeur, détermine les dimensions du terrain.
Exercice 27
Nogaye dépense les trois cinquième de son argent pour acheter un livre.
Elle donne ensuite le quart du reste à sa sœur Ami. Elle se retrouve après avec seulement $12\,000$ francs.
Quelle somme d'argent avait Nogaye ?
Exercice 28
Un avion effectue la ligne Dakar-Bamako-Ouaga-Abidjan.
A l'embarquement à Dakar, les $\dfrac{3}{4}$ des sièges sont occupés.
A l'escale de Bamako, $45$ passagers descendent et $27$ montent, l'avion est plein aux $\dfrac{2}{3}$.
A l'escale de Ouaga la moitié des passagers descend et $25$ montent.
1) Quel est le nombre de places réservés aux passagers ?
2) Quel est le nombre de passagers débarquant à Abidjan ?

Commentaires
Anonyme (non vérifié)
ven, 03/15/2019 - 14:21
Permalien
Correction
pierart (non vérifié)
lun, 11/16/2020 - 14:30
Permalien
correction
brahim (non vérifié)
mer, 04/20/2022 - 17:54
Permalien
Pour être un champion en
Anonyme (non vérifié)
dim, 04/14/2019 - 16:11
Permalien
dem
Anonyme (non vérifié)
sam, 10/19/2019 - 15:57
Permalien
Bonjour j'ai besoin de la
Anonyme (non vérifié)
mar, 02/18/2020 - 17:38
Permalien
correction
Anonyme (non vérifié)
sam, 07/10/2021 - 20:32
Permalien
Ah bon pourquoi
Anonyme (non vérifié)
sam, 07/10/2021 - 20:32
Permalien
Ah bon pourquoi
Anonyme (non vérifié)
sam, 07/10/2021 - 20:32
Permalien
Ah bon pourquoi
Ajouter un commentaire