Vous êtes ici

Solution des exercices : Grandeurs physiques et mesures - 4e

Classe:

Quatrième

Exercice 1

Complétons le tableau suivant :

$$\begin{array}{|c|c|c|c|} \hline \text{Grandeurs}&\text{Nom de l'unité}&\text{Symbole de}&\text{Instrument de}\\ \text{physiques}& &\text{l'unité}&\text{mesure}\\ \hline\text{longueur}&\text{mètre}&m&\text{règle graduée}\\ \hline\text{masse}&\text{kilogramme}&kg&\text{balance}\\ \hline\text{volume}&\text{mètre cube}&m^{3}&\text{burette,}\\&&&\text{éprovette graduée}\\ \hline\text{intensité}&&&\\ \text{du courant}&\text{ampère}&A&\text{ampèremètre}\\ \text{électrique}&&&\\ \hline\text{temps}&\text{seconde}&s&\text{chronomètre}\\ \hline\text{température}&\text{degré Kelvin}&^{\circ}K&\text{thermomètre}\\ \hline\end{array}$$

Exercice 2

1) Complétons le tableau en précisant pour chaque instrument de mesures, la grandeur physique mesurée :

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{balance}&\text{chronomètre}&\text{thermomètre}&\text{sablier}&\text{règle}&\text{ampèremètre}\\ & & & &\text{graduée}&\\ \hline\text{masse}&\text{temps}&\text{température}&\text{intervalle}&\text{longuaur}&\text{intensité du}\\&&&\text{de temps}&&\text{courant électrique}\\ \hline \end{array}$$

2) Indiquons pour chaque instrument de mesure une personne qui a l'habitude de l'utiliser.

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{balance}&\text{chronomètre}&\text{thermomètre}&\text{ruban-mètre}&\text{multimètre}&\text{manomètre}\\ \hline\text{commerçant}&\text{arbitre}&\text{médecin}&\text{maçon}&\text{électricien}&\text{frigoriste}\\ \hline\end{array}$$

Exercice 3

Classons les mots dans un tableau à deux colonnes, une pour les grandeurs physiques et l'autre pour les unités.

$$\begin{array}{|l|c|}\hline\text{Grandeurs physiques}&\text{Unités}\\ \hline\text{distance}&\text{kilomètres}\\ \hline\text{volume}&dm^{3}\\ \hline\text{masse}&kg\\ \hline\text{durée (temps)}&\text{heures}\\ \hline\text{température}&^{\circ}C\\ \hline\end{array}$$

Exercice 4

1) Donnons l'écriture scientifique des nombres suivants :

Écrire un nombre en notation scientifique revient à l'écrire sous la forme :

$$a\times 10^{n}$$

avec : $\ 1\leq a<10\quad\text{ ou}\quad -10<a\leq -1\ $ et $\ n$ un entier relatif.

a) On a : $178\;m=178.0\;m$

On peut alors déplacer $2$ fois la virgule vers la gauche jusqu'au dernier chiffre significatif.

Or, déplacer $n$ fois la virgule à gauche, se compense en multipliant par $10^{n}$

Donc, $178.0\;m=1.78\times 10^{2}\;m$

b) Soit : $15386\;kg=15386.0\;kg$

En déplaçant $4$ fois la virgule vers la gauche, on arrive au dernier chiffre significatif.

Par suite, $15386\;kg=1.5386\times 10^{4}\;kg$

c) On a : $6000\;W=6\times 1000=6\times 10^{3}\;W$

d) Soit le nombre $0.000876$

En déplaçant $4$ fois la virgule vers la droite, on dépasse le premier chiffre significatif.

Comme déplacer $n$ fois la virgule vers la droite, se compense en multipliant par $10^{-n}$ alors, $$0.000876=8.76\times 10^{-4}$$

2) Donnons l'ordre de grandeur des valeurs numériques suivantes :

Par définition, l'ordre de grandeur d'une valeur numérique est la puissance de dix entière la plus proche de cette valeur.

a) Soit le nombre $6370$

En écriture scientifique, on a : $6370=6.370\times 10^{3}$

On constate que le premier chiffre significatif $(6)$ est strictement supérieur à $5$ donc, l'ordre de grandeur du nombre $6370=6.370\times 10^{3}$ est égal à la puissance de $10$ suivante ; c'est-à-dire $10^{3+1}=10^{4}.$

Ainsi, $6370\sim 10^{4}$

b) Soit le nombre $1.035\times 10^{3}$ alors, son premier chiffre significatif $(1)$ est strictement inférieur à $5.$

Par conséquent, l'ordre de grandeur de ce nombre est la puissance de $10$ associée $(10^{3}).$

D'où, $1.035\times 10^{3}\sim 10^{3}$

c) Pour le nombre $2.876\times 10 ^{2}$, on constate que son premier significatif $(2)$ est strictement inférieur à $5.$

Donc, son ordre de grandeur est la puissance de $10$ associée ; c'est-à-dire $10^{2}.$

Par suite, $2.876\times 10^{2}\sim 10^{2}$

d) Comme $9>5$ alors l'ordre de grandeur du nombre $9.554\cdot 10^{-3}$ est égal à la puissance de $10$ suivante ; à savoir $10^{-3+1}=10^{-2}.$

Ainsi, $9.554\times 10^{-3}\sim 10^{-2}$

3) Donner les chiffres significatifs des nombres suivants :

a) $0.0041$

On a deux chiffres significatifs : $4\ $ et $\ 1$

b) $0.2075$

On obtient quatre chiffres significatifs : $2\;,\ 0\;,\ 7\ $ et $\ 5$ dans cet ordre.

c) Pour le nombre $6.0532890$, tous les chiffres sont significatifs

d) Pour le nombre $0.0000010$, on obtient deux chiffres significatifs : $1\ $ et $\ 0$ (c'est le $0$ qui se trouve le plus à droite).

Exercice 5

1) Convertissons les masses suivantes :

a) $1\;kg=1\,000\;g=1\times 10^{3}\;g$

b) $1\;g=0.001\;kg=1\times 10^{-3}\;kg$

c) $0.9\;hg\ $ en $\ mg$

On a : $1\;hg=1\times 10^{5}\;mg$ donc, $0.9\;hg=0.9\times 10^{5}\;mg=9\times 10^{4}\;mg$

d) $1.8\;kg\ $ en $\ g$

Comme $1\;kg=1\times 10^{3}\;g$ alors, $1.8\;kg=1.8\times 10^{3}\;g$

2) Convertissons les volumes suivants :

a) $25000\;mL\ $ en $\ hL$

On sait que : $1\;mL=1\times 10^{-5}\;hL$

Donc, $25000\;mL=25000\times 10^{-5}\;hL=0.25\;hL$

b) $0.25\;hL\ $ en $\ L$

On a : $1\;hL=1\times 10^{2}\;L$

Par suite, $0.25\;hL=0.25\times 10^{2}\;L=25\;L$

c) $87\;L\ $ en $\ dL$

Comme $1\;L=1\times 10^{1}\;dL$ alors, $87\;L=87\times 10^{1}\;dL=870\;dL$

d) $0.03\;L\text{ en }mL$

Soit : $1\;L=1\times 10^{-3}\;mL$

Alors, $0.03\;L=0.03\times 10^{-3}\;mL=30\;mL$

e) $1250\;cm^{3}\ $ en $\ dm^{3}$

On a : $1\;cm^{3}=1\times 10^{-3}\;dm^{3}$

Donc, $1250\;cm^{3}=1250\times 10^{-3}\;dm^{3}=1.25\;dm^{3}$

f) $1.5\;dm^{3}\ $ en $\ m^{3}$

On sait que : $1\;dm^{3}=1\times 10^{-3}\;m^{3}$

Par suite, $1.5\;dm^{3}=1.5\times 10^{-3}\;m^{3}$

g) $1.5\;dm^{3}\ $ en $\ mL$

Comme $1\;dm^{3}=1\times 10^{3}\;mL$ alors, $1.5\;dm^{3}=1.5\times 10^{3}\;mL$

h) $125\;mL\text{ en }dm^{3}.$

On a : $1\;mL=1\times 10^{-3}\;dm^{3}$

Ainsi, $125\;mL=125\times 10^{-3}\;dm^{3}=1.25\cdot 10^{-1}\;dm^{3}$

Exercice 6

1) Écrivons à l'aide d'une puissance de $10$, les nombres suivants :

a) $0.000000000001=10^{-12}$

b) $100000000=10^{8}$

c) $1=10^{0}$

d) $10000=10^{4}$

2) Écrivons à l'aide d'une puissance de $10$, les nombres suivants :

a) $\text{un milliard}=1\,000\,000\,000=10^{9}$

b) $\text{un millième}=\dfrac{1}{1\,000}=0.001=10^{-3}$

c) $\text{cent mille}=100\,000=10^{5}$

d) $\text{un millionième}=\dfrac{1}{1\,000\,000}=0.000001=10^{-6}$

3) Exprimons sous la forme d'une puissance de $10$, les nombres suivants :

On utilise les propriétés suivantes :

$$a^{n}\times a^{m}=a^{(n+m)}\quad\text{et}\quad a\times 10^{n}+b\times 10^{n}=(a+b)\times 10^{n}$$

a) $10^{5}\times 10^{7}=10^{5+7}=10^{12}$

b) $10^{-11}\times 10^{3}\times 10^{2}=10^{-11+3+2}=10^{-6}$

c) On a : $3.1\times 10^{5}=310\times 10^{3}$ donc,

$\begin{array}{rcl} 3.1\times 10^{5}+4.8\times 10^{3}&=&310\times 10^{3}+4.8\times 10^{3}\\ \\&=&(310+4.8)\times 10^{3}\\ \\&=&314.8\times 10^{3}\end{array}$

En écrivant le nombre $314.8$ en notation scientifique, on obtient :

$$314.8=3.148\times 10^{2}$$

Par suite,

$\begin{array}{rcl} 314.8\times 10^{3}&=&3.148\times 10^{2}\times 10^{3}\\ \\&=&3.148\times 10^{2+3}\\ \\&=&3.148\times 10^{5}\end{array}$

D'où, $3.1\times 10^{5}+4.8\times 10^{3}=3.148\times 10^{5}$

Exercice 7

1) Parmi les nombres suivants, $5.23\times 10^{12}$ et d) $-1.47\times 10^{6}$ sont écrits en notation scientifique

$0.251\times 10^{3}$ n'est pas écrit en notation scientifique car $0.251<1$

$72.43\times 10^{-8}$ n'est pas écrit en notation scientifique car $72.43>1$

2) Écrivons les nombres suivants en notation scientifique

a) $7283=7.283\times 10^{3}$

b) $12.47=1.247\times 10^{1}$

c) $0.67\times 10^{2}=6.7\times 10^{1}$

d) $0.0058=5.8\times 10^{-3}$

Exercice 8

Calculons et donnons les résultats sous la forme d'une écriture scientifique :

$\begin{array}{rcl} 150\times 10^{3}\times 8\times 10^{5}&=&150\times 8\times 10^{3}\times 10^{5}\\ \\&=&1200\times 10^{3+5}\\ \\&=&1200\times 10^{8}\\ \\&=&1.200\times 10^{3}\times 10^{8}\\ \\&=&1.2\times 10^{3+8}\\ \\&=&1.2\times 10^{11}\end{array}$

Donc, $\boxed{150\times 10^{3}\times 8\times 10^{5}=1.2\times 10^{11}}$

$\begin{array}{rcl} 2\times 10^{9}\times 7\times 10^{6}&=&2\times 7\times 10^{9}\times 10^{6}\\ \\&=&14\times 10^{9+6}\\ \\&=&14\times 10^{15}\\ \\&=&1.4\times 10^{1}\times 10^{15}\\ \\&=&1.4\times 10^{1+15}\\ \\&=&1.4\times 10^{16}\end{array}$

Ainsi, $\boxed{2\times 10^{9}\times 7\times 10^{6}=1.4\times 10^{16}}$

$\begin{array}{rcl} 2\times 10^{3}\times 5\times 10^{-5}&=&2\times 5\times 10^{3}\times 10^{-5}\\ \\&=&10\times 10^{3-5}\\ \\&=&10^{1}\times 10^{-2}\\ \\&=&10^{-1}\end{array}$

D'où, $\boxed{2\times 10^{3}\times 5\times 10^{-5}=10^{-1}}$

$\begin{array}{rcl} 3\times 10^{2}\times 1.2\times 10^{-5}&=&3\times 1.2\times 10^{2}\times 10^{-5}\\ \\&=&3.6\times 10^{2-5}\\ \\&=&3.6\times 10^{-3}\end{array}$

Donc, $\boxed{3\times 10^{2}\times 1.2\times 10^{-5}=3.6\times 10^{-3}}$

Exercice 9

Notre planète est entourée d'une couche d'air dont la plus grande partie est répartie sur une épaisseur d'une dizaine de kilomètres.

On appelle pression atmosphérique la pression qu'exerce cette couche d'air sur les corps à la surface de la Terre.

Le symbole de la pression est $P.$

La pression atmosphérique est une donnée précieuse pour la météorologie car les mouvements des masses d'air en altitude sont responsables de l'évolution du climat.

La mesure de la pression atmosphérique est donc nécessaire pour prévoir les conditions climatiques. L'unité légale de la pression est le pascal $($symbole : $Pa).$

La pression atmosphérique est mesurée par un appareil de mesure : le baromètre. Certains baromètres sont gradués en hectopascals $($symbole : $hPa)$ ou en millibars $($symbole : $mbar).$

D'autres baromètres sont gradués en hauteur de colonne de mercure $($symbole : $mm\,Hg).$

1) L'instrument de mesure cité dans ce texte est le baromètre

2) Le baromètre mesure la pression atmosphérique

3) Le symbole de la pression $P$

4) L'unité de pression dans le système international est le Pascal. Son symbole est : $Pa$

5) Les autres unités de pression citées dans le texte sont :

$-\ $ hectopascals : $hPa$

$-\ $ millibars : $mbar$

$-\ $ millimètre de mercure : $mm\,Hg$

6) Convertissons un hectopascal en pascal.

On a : $1\,hPa=100\,Pa$

7) A part les laboratoires de météorologie, on trouve les appareils qui permettent de mesurer la pression dans les laboratoires de physique, de chimie, dans les stations de gonflage, dans les usines de transformation des aliments, dans les usines de montage par injection.

Ces appareils de mesure de la pression atmosphérique sont donc utilisés par les physiciens, les chimistes, les architectes, les agents des stations de gonflage et certains ingénieurs et techniciens d'usines de transformations ou de montage.

Exercice 10

Complétons la phrase ci-dessous

L'écriture scientifique d'un nombre est donnée par le produit d'un nombre décimal compris entre $1\ $ et $\ 10$ par une puissance entière de $10.$

Exercice 11 Conversion d'unités

Effectuons des conversions suivantes

1) $3\;km=3\times 10^{2}\;dam=3\times 10^{3}\;m=3\times 10^{6}\;mm$

2) $1.5\;dm=1.5\times 10^{-1}\;m=1.5\times 10^{2}\;mm$

3) $62\;g=62\times 10^{3}\;mg=62\times 10^{-3}\;kg=62\times 10^{-6}\;t$

4) $4.2\;dm^{3}=4.2\times 10^{3}\;cm^{3}=4.2\times 10^{3}\;ml$

5) $0.9\;hl=9\times 10^{-2}\;m^{3}=90\;l=9\times 10^{4}\;cm^{3}$

6) $1.3\cdot 10^{-6}km^{2}=1.3\;m^{2}=1.3\times 10^{2}\;dm^{2}=1.3\times 10^{6}\;mm^{2}$

Exercice 13 Chiffres significatifs et notation scientifique

Les données ci-dessous correspondent à des résultats de mesure de longueur exprimés en mètre.

Pour chaque mesure, le nombre de chiffres significatifs pour chaque mesure et exprimons ces données en notation scientifique.

$$\begin{array}{|c|c|c|c|c|c|c|} \hline&A&B&C&D&E&F\\ \hline\text{résultats}&&&&&&\\\text{de}&5.43&58.0&1200&0.0005&4804.02&20.300\\\text{mesure}&&&&&&\\\hline\text{nombre de}&&&&&&\\\text{chiffres}&3&3&4&1&6&5\\\text{significatifs}&&&&&&\\\hline\text{expression}&&&&&&\\\text{en notation}&5.43\cdot 10^{0}&5.80\cdot 10^{1}&1.200\cdot 10^{3}&5\cdot 10^{-4}&4.80402\cdot 10^{3}&2.0300\cdot 10^{1}\\\text{scientifique}&&&&&&\\ \hline\end{array}$$

Exercice 14 Se servir du double-décimètre

Une longueur est mesurée avec une règle graduée en $cm.$

1) L'écriture correcte de la valeur mesurée est la valeur affichée en b) : $13.0\;cm$

2) Donnons une explication au rejet de chacune des autres valeurs.

Comme le double décimètre est divisé en centimètres et en millimètres alors, il ne permet pas de mesurer une longueur au $\dfrac{1}{10}$ ou au $\dfrac{1}{100}$ de millimètre $(mm)$ près.

D'où, le rejet des valeurs affichées en a) et c).

De plus, la précision du double décimètre étant de l'ordre de $1\;mm$ près donc, la valeur en a), donnée à $1\;cm$ près ; soit $10\;mm$ près peut être entachée d'erreurs. D'où, son rejet.

Exercice 15 Précision d'une mesure

Les écritures du résultat de la mesure d'une longueur sont notées ci-dessous.

1) Entourons la lettre qui correspond à la mesure la plus précise

a) $15.2\;cm$

b) $0.152\;m$

c) $152\;mm$

$\boxed{\text{d) }152.0\;mm}$

e) $152\cdot 10^{-3} m$

2) Justification de ce choix.

En effet, on constate que ce nombre comporte $4$ chiffres significatifs tandis que les autres n'en comptent que $3.$ Donc, $152.0\;mm$ est la mesure la plus précise (trois valeurs sont connues avec certitude alors qu'avec les autres mesures on ne connait que deux valeurs).

Exercice 16 Précision d'un calcul à partir de valeurs mesurées

Les mesures des dimensions de deux champs rectangulaires ont donné les résultats suivants :

$\centerdot\ $ Champ 1 : $L_{1}=121.9\;m\ $ et $\ \ell_{1}=65.0\;m$

$\centerdot\ $ Champ 2 : $L_{2}=1.46\;m\ $ et $\ \ell_{2}=0.78\;m$

1) Calculons les aires $A_{1}\ $ et $\ A_{2}$ des surfaces correspondantes en respectant le nombre de chiffres significatifs.

En effet, dans une multiplication le résultat doit avoir le même nombre de chiffres significatifs que le facteur avec le moins de chiffres significatifs.

Ainsi, pour le champ 1 on a :

$\begin{array}{rcl} A_{1}&=&L_{1}\times\ell_{1}\\ \\&=&121.9\times 65.0\\ \\&=&7\,923.5\end{array}$

Comme le facteur $2$, avec $3$ chiffres significatifs, est le facteur comportant le moins de chiffres significatifs alors,

$$\boxed{A_{1}=7.92\times 10^{3}\;m^{2}}$$

pour le champ 2, on a :

$\begin{array}{rcl} A_{2}&=&L_{2}\times\ell_{2}\\ \\&=&1.46\times 0.78\\ \\&=&1.1388\end{array}$

On constate que le premier facteur compte $3$ chiffres significatifs et que le deuxième facteur en compte $2$ donc, le résultat sera donné avec $2$ chiffres significatifs.

Ainsi, en arrondissant au dixième on obtient :

$$\boxed{A_{2}=1.1\;m^{2}}$$

2) Calculons les périmètres correspondants.

Il faut noter que dans une addition le résultat doit avoir le même nombre de chiffres après la virgule que le terme de l'addition qui en a le moins.

Donc, pour le champ 1 on obtient :

$\begin{array}{rcl} P_{1}&=&(L_{1}+\ell_{1})+(L_{1}+\ell_{1})\\ \\&=&(121.9+65.0)+(121.9+65.0)\\ \\&=&186.9+186.9\\ \\&=&373.8\end{array}$

Ainsi, $$\boxed{P_{1}=373.8\;m}$$

pour le champ 2 on a :

$\begin{array}{rcl} P_{2}&=&(L_{2}+\ell_{2})+(L_{2}+\ell_{2})\\ \\&=&(1.46+0.78)+(1.46+0.78)\\ \\&=&2.24+2.24\\ \\&=&4.48\end{array}$

D'où, $$\boxed{P_{2}=4.48\;m}$$

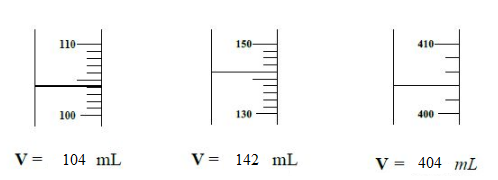
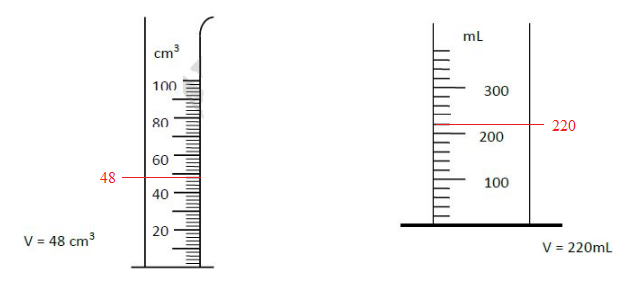
Exercice 17 Disque circulaire

Le périmètre d'un disque circulaire de rayon $R$ est donné par $C=2\pi R$ et l'aire de sa surface a pour l'expression $A=\pi R^{2}.$

Un disque circulaire à un diamètre $D=20.0\;cm$

1) Déterminons son périmètre.

Soit : $C=2\pi R$ or, $\ R=\dfrac{D}{2}$

Donc, $C=2\pi\times\dfrac{D}{2}=\pi\times D$

A.N : $C=3.14\times 20.0=62.8$

D'où, $$\boxed{C=62.8\;cm}$$

2) Calculons l'aire de sa surface.

On a :$A=\pi R^{2}$ or, $\ R=\dfrac{D}{2}$

Donc, $A=\pi\times\dfrac{D^{2}}{4}$

A.N : $A=3.14\times\dfrac{(20.0)^{2}}{4}=314$

D'où, $$\boxed{A=314\;cm^{2}}$$

Remarque : Les résultats sont conformes avec les données car, on a $3$ chiffres significatifs.

Exercice 18 Détermination de volume

1) Indiquons la valeur de chaque volume $($en $mL)$ mesuré ci-dessous.

2) Représentons dans chaque cas le volume indiqué à l'aide d'un trait horizontal.

Auteur:

Aliou ndiaye

Commentaires

Anonyme (non vérifié)

jeu, 12/26/2019 - 22:14