Corrigé BFEM Maths 2015

Exercice 1


 
 

 
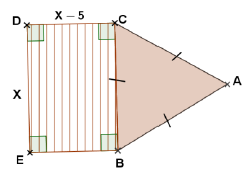
La figure codée ci-dessus est une représentation d'un terrain formé de deux parcelles, l'une triangulaire et l'autre rectangulaire.
 
1) le périmètre de la parcelle $ABC$ est : $P_{ABC}=3x.$
 
Celui de la parcelle $BCDE$ est $P_{BCDE}=4x-10.$
 
"Le périmètre de la parcelle $ABC$ est strictement plus grand que celui de la parcelle $BCDE$" signifie $3x>4x-10\ $ et $\ x>5$ (puisque $x-5>0$) ce qui donne $5<x<10$
 
L'ensemble des valeurs de $x$ pour lesquelles le périmètre de $ABC$ est strictement plus grand que celui de $BCDE$ est $]5\;;\ 10[.$
 
2) a) La hauteur $h$ du triangle $ABC$ équilatéral est telle que : $h^{2}+\left(\dfrac{x}{2}\right)^{2}=x^{2}$
 
donc, $h^{2}=x^{2}-\dfrac{x^{2}}{4}=\dfrac{3x^{2}}{4}$ et par suite, $h=x\dfrac{\sqrt{3}}{2}$
 
Ainsi, l'aire de la parcelle $ABC$ est $$\mathcal{A}_{ABC}=x\times x\dfrac{\sqrt{3}}{2}\times\dfrac{1}{2}=\dfrac{x^{2}\sqrt{3}}{4}$$
 
b) L'aire de la parcelle $BCDE$ est $$\mathcal{A}_{BCDE}=x(x-5)=x^{2}-5x$$
 
"L'aire de la parcelle $BCDE$ est égale à $\dfrac{3x^{2}}{4}$" signifie : $\dfrac{3x^{2}}{4}=x^{2}-5x$ et $x$ strictement supérieur à 5.
 
D'où : $x\left(x\dfrac{3}{4}-x+5\right)=0\ $ ou $\ x\left(\dfrac{-x}{4}+5\right)=0$
 
Ce qui donne : $x=0\ $ ou $\ x=20.$ Puisque $x$ est strictement supérieur à 5 alors, $x=20.$
 
La longueur de grillage achetée est $\ell=\dfrac{90000}{1500}\;m=60\;m$
 
La longueur du grillage en fonction de $x$ est : $(3x-10+2x)-2$
 
Ainsi, $(3x-10+2x)-2=60$
 
Donc, $5x=72.$ D'où : $x=14.4$

Exercice 2

1) Le prix du ticket de section acheté par l'usager est le caractère statistique étudié.
 
2) Cette entreprise a transporté 7200 ce jour.
 
3) Les modalités du caractère sont : 100F, 150F, 200F, 250F, 300F et 350F
 
4) Le nombre d’usagers ayant acheté un ticket valant moins de 250F est : 4360
 
5) Le nombre d'usagers ayant acheté un ticket valant au moins à 250F est : 2840
 
6) Le prix médian du ticket de section est $Mé=200\;F$
 
7) le prix moyen du ticket de section est : $\dfrac{3575}{18}\;F$
 
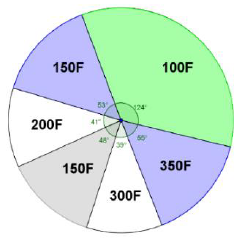
8) le diagramme circulaire de la série
 
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Prix du ticket}& & & & & & \\ \text{de section}&100&150&200&250&300&350 \\ \text{en FCFA}& & & & & & \\ \hline\text{Nombre de tickets}&2\,480&1\,060&820&960&780&1\,100 \\ \hline\text{Angles en degrés}&124&53&41&48&39&55 \\ \hline\end{array}$$

 

 
 

Exercice 3

1) $a\times m+b\times n+c=0$
 
2) $x\times b-a\times y=0$
 
3) $a\times p=-1$
 
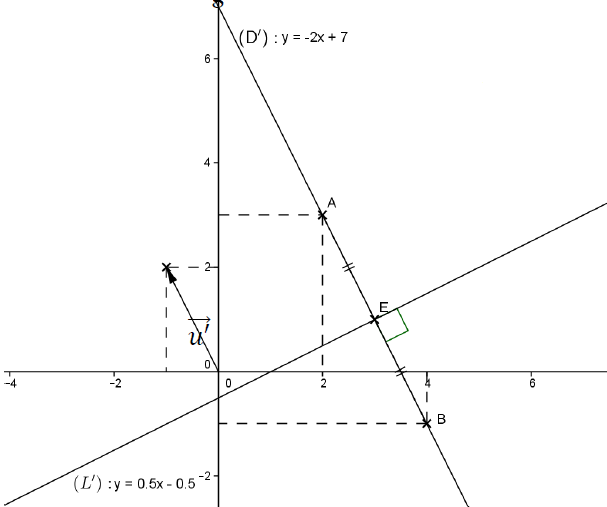
4) a) On obtient : $(D')\ :\ 2x+y-7=0$
 
b) On a : $2\times 4-1-7=8-8=0$ donc $B\in(D')$
 
c) $(D')$ a pour coefficient directeur $-2$ donc $(L')$ a pour coefficient directeur $\dfrac{1}{2}$ d'où $(L')\ :\ y=\dfrac{1}{2}x+b$
 
$\begin{pmatrix} 3\\ 1\end{pmatrix}$ , milieu de $[A'B]$ appartient à $(L')$ donc, $b=-\dfrac{1}{2}.$ D'où : $(L')\ :\ y=\dfrac{1}{2}x-\dfrac{1}{2}$
 
d) $IA'=IB=\sqrt{10}$
 
e) $A'I=IB$ alors $A'BI$ est Isocèle en $I.$ Comme $E$ est le milieu de $[A'B]\;,\ IE$ est la hauteur de $A'BI$ relative au sommet $I$
 
Donc, $Aire(A'IB)=\dfrac{IE\times A'B}{2}=\dfrac{\sqrt{5}\times 2\sqrt{5}}{2}=5$
 
f) Figure

 
 

 

Commentaires

Anonyme (non vérifié)

mar, 02/05/2019 - 15:35

j ai besoin des autres corriges

Anonyme (non vérifié)

mer, 07/15/2020 - 15:50

interressant et utile. merci

Anonyme (non vérifié)

jeu, 09/03/2020 - 07:15

Le texte est très plein .comment peut-on faire pour le diminuer

Cherif (non vérifié)

jeu, 09/03/2020 - 12:11

Si tu connecte avec smartphone fait double tape pour réduire ou tu tapes sur rotation automatique pour allonger le téléphone

Anonyme (non vérifié)

dim, 01/17/2021 - 22:32

Ttggggsd

Anonyme (non vérifié)

mar, 11/08/2022 - 09:19

C'est bien

Anonyme (non vérifié)

sam, 04/06/2024 - 15:04

Pourquoi IA'=IB=√10

Ajouter un commentaire