Distance - 4e
Classe:
Quatrième
I. Distance sur le plan
I.1. Activité
1) Tracer un segment $[AB]$ de longueur $5\;cm$
2) Marquer un point $C$ sur $[AB]$ et un point $D\notin[AB]$
3) a) Quelle est la distance du point $A$ au point $B\ ?$
b) Comparer les longueurs $AB\ $ et $\ AC+CB$ puis $AB\ $ et $\ AD+DB$
c) Peut-on trouver un point $N$ tel que la longueur du segment $[AN]$ soit nulle ?
Solution
1) et 2)
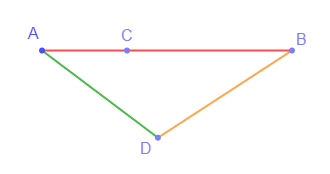
3) a) La distance du point $A$ au point $B$ est de $5\;cm$
b) $AB=5\;cm\;;\ AC=1.7\;cm\ $ et $\ CB=3.3\;cm$
Donc, $AC+CB=1.7\;cm+3.3\;cm=5\,cm=AB$
D'où, $\boxed{AC+CB=AB}$
On a : $AD=2.9\;cm\ $ et $\ DB=3.2\;cm$
Alors, $AD+DB=2.9\;cm+3.2\;cm=6.1\;cm$
Donc, $\boxed{AB<AD+DB}$
c) Si $N=A$ alors, la distance de $A\ $ à $\ N$ est nulle.
I.2. Définition
La distance d'un point $A$ à un point $B$ est la longueur du segment $[AB].$ On le note :
$$AB\quad\text{ou}\quad\mathrm{d}(A\;,\ B)$$
Propriétés
Soit $A\ $ et $\ B$ deux points du plan.
$\centerdot\ AB=0$ si, et seulement si, $A=B\ $ $(A\ $ et $\ B$ sont confondus)
$\centerdot\ AB=BA\ \ (\mathrm{d}(A\;,\ B)=\mathrm{d}(B\;,\ A))$
$\centerdot\ $ Pour tout point du plan :
$\quad AB=AM+MB\ $ si $\ M\in[AB]$
$\quad AB<AM+MB\ $ si $\ M\notin[AB]$
Conclusion
Si $A\ $ et $\ B$ sont deux points du plan alors, pour tout point $M$ du plan on a :
$$AB\leq AM+MB\quad(\text{Inégalité triangulaire})$$
II. Positions relatives de deux cercles
Soient $\mathcal{C}(O\;,\ r)\ $ et $\ \mathcal{C}'(O'\;,\ r')$ deux cercles du plan.
II.1. $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont tangents extérieurement
Si $OO'=r+r'$ alors, les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont dits tangents extérieurement.
Exemple
Marquer deux points $O\ $ et $\ O'$ tels que $OO'=5\;cm.$
Construire les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ de centres $O\ $ et $\ O'$ respectivement et de rayon $r=2\;cm\ $ et $\ r'=3\;cm$
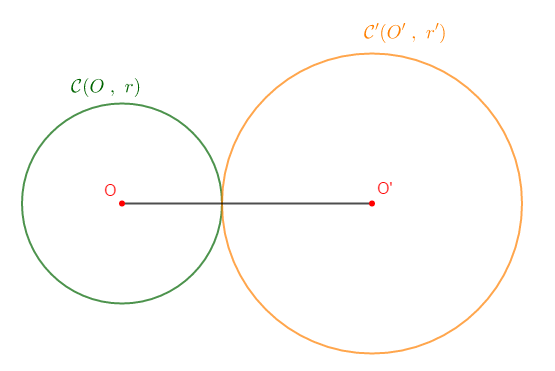
Soit : $OO'=5\;cm$, on a :
$r+r'=2\;cm+3\;cm=5\;cm$ donc, $OO'=r+r'$
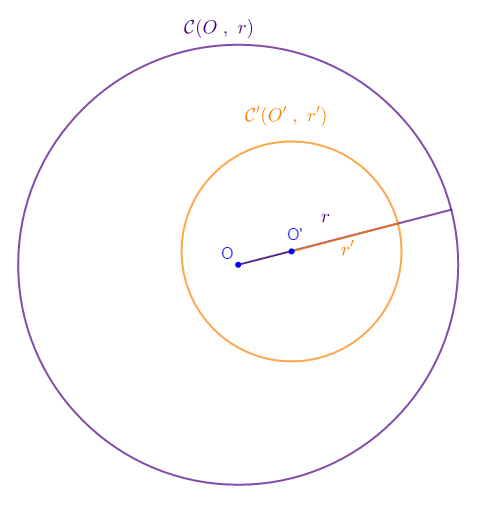
II.2. $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont tangents intérieurement
Si $OO'=|r-r'|$ alors, les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont dits tangents intérieurement.
Exemple
Marquer deux points $O\ $ et $\ O'$ tels que $OO'=1\;cm.$
Construire les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ de centres $O\ $ et $\ O'$ et de rayon $r=2\;cm\ $ et $\ r'=3\;cm$ respectivement.
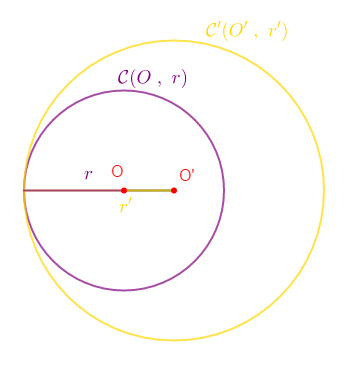
On a :
$\begin{array}{rcl}|r-r'|&=&|2-3|\\ \\&=&|-1|\\ \\&=&1\;cm \end{array}$
Or, $OO'=1\;cm$ donc, $|r-r'|=OO'$
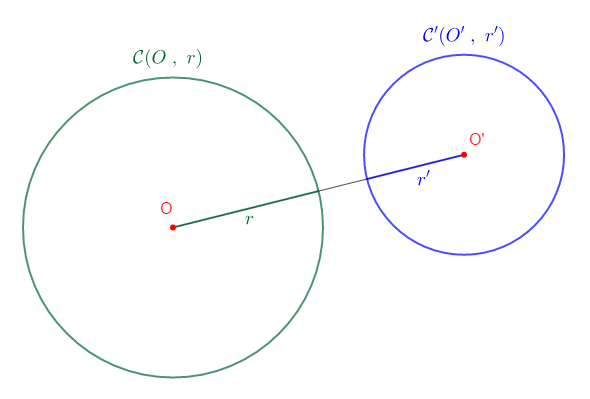
II.3. $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont disjoints extérieurement
Si $OO'$ est supérieure à $r+r'$ alors, les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont disjoints extérieurement.
Exemple
Marquer deux points $O\ $ et $\ O'$ tels que $OO'=6\;cm.$
Construire les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ de centres $O\ $ et $\ O'$ et de rayon $r=2\;cm\ $ et $\ r'=3\;cm$ respectivement.

On a :
$r+r'=3\;cm+2\;cm=5\;cm$
Or, $OO'=6\;cm$ donc, $OO'>r+r'$
II.4. $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont disjoints intérieurement
Si $OO'$ est inférieure à $|r-r'|$ alors, les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont disjoints intérieurement.
Exemple
Marquer deux points $O\ $ et $\ O'$ tels que $OO'=1\;cm.$
Construire les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ de centres $O\ $ et $\ O'$ et de rayon $r=4\;cm\ $ et $\ r'=2\;cm$ respectivement.

On a :
$\begin{array}{rcl}|r-r'|&=&|4-2|\\ \\&=&|2|\\ \\&=&2\;cm \end{array}$
Or, $OO'=1\;cm$ donc, $OO'<|r-r'|$
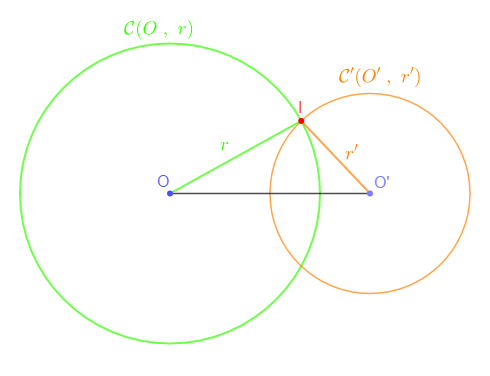
II.4. $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont sécants
Si $OO'$ est inférieure à $r+r'$ et supérieure à $|r-r'|$ alors, les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ sont sécants.
Exemple
Marquer deux points $O\ $ et $\ O'$ tels que $OO'=4\;cm.$
Construire les cercles $\mathcal{C}\ $ et $\ \mathcal{C}'$ de centres $O\ $ et $\ O'$ et de rayon $r=3\;cm\ $ et $\ r'=2\;cm$ respectivement.

Soit : $r+r'=3\;cm+2\;cm=5\;cm\ $ et $\ |r-r'|=|3\;cm-2\;cm|=1\;cm$
Comme $OO'=4\;cm$ alors, on a : $OO'<r+r'\ $ et $\ OO'>|r-r'|$
III. Critère d'existence d'un triangle
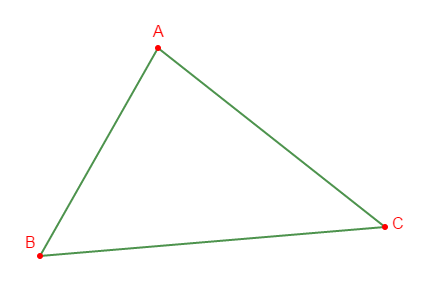
III.1. Activité
Soit $ABC$ un triangle quelconque.
1) En utilisant l'inégalité triangulaire, montrer que :
$$AB<BC+AC\;,\quad BC<AB+AC\;,\quad AC<AB+BC$$
2) En déduire que :
$BC-AC<AB<BC+AC$
$AB-AC<BC<AB+AC$
$AB-BC<AC<AB+BC$
Solution
1) En utilisant l'inégalité triangulaire, on a :
$C\notin[AB]$ donc, $AB<BC+AC\quad(1)$
$A\notin[BC]$ alors, $BC<AB+AC\quad(2)$
$B\notin[AC]$ donc, $AC<AB+BC\quad(3)$
2) Démontrons que : $BC-AC<AB<BC+AC$
D'après (2), on a :
$\begin{array}{rcrcl} BC<AB+AC&\Rightarrow&BC-AC&<&AB+AC-AC\\ \\&\Rightarrow&BC-AC&<&AB\end{array}$
Donc, $BC-AC<AB$
Or, d'après (1) on a : $AB<BC+AC$ d'où, finalement :
$$BC-AC<AB<BC+AC$$
Démontrons que : $AB-AC<BC<AB+AC$
D'après (1), on a :
$\begin{array}{rcrcl} AB<BC+AC&\Rightarrow&AB-AC&<&BC+AC-AC\\ \\&\Rightarrow&AB-AC&<&BC\end{array}$
Ainsi, $AB-AC<BC$
Comme d'après (2) $BC<AB+AC$ alors, on obtient :
$$AB-AC<BC<AB+AC$$
Démontrons que : $AB-BC<AC<AB+BC$
De la même manière, en considérant la relation (1), on obtient :
$\begin{array}{rcrcl} AB<BC+AC&\Rightarrow&AB-BC&<&BC+AC-BC\\ \\&\Rightarrow&AB-BC&<&AC\end{array}$
Donc, $AB-BC<AC$
Or, d'après (3) on a : $AC<AB+BC$ d'où, finalement :
$$AB-BC<AC<AB+BC$$
III.2. Propriété
Dans un triangle, la longueur d'un côté est toujours comprise entre la somme et la différence des longueurs des deux autres côtés.
Application
Soit $ABM$ un triangle tel que :
$$AB=7\;cm\quad\text{et}\quad AM=4\;cm$$
1) Peut-on avoir $BM=5\;cm\ ?$ Pourquoi ?
1) Peut-on avoir $BM=2\;cm\ ?$ Pourquoi ?
Solution
1) On a : $AB-AM<BM<AB+AM.$ Soit :
$AB-AM=7\;cm-4\;cm=3\;cm$
$AB+AM=7\;cm+4\;cm=11\;cm$
Comme $3\;cm<5\;cm<11\;cm$ alors, on peut bien avoir $BM=5\;cm$
2) $BM$ ne vérifie pas $AB-AM<BM<AB+AM$ donc, on ne peut pas avoir $BM=2\;cm.$
IV. Distance d'un point à une droite
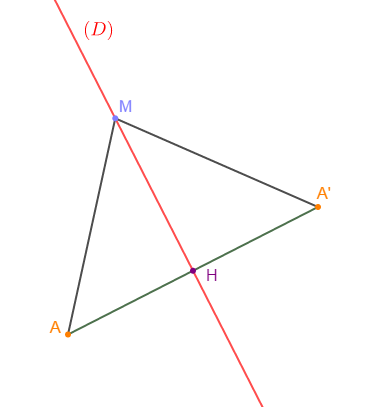
IV.1. Activité
Soit $(D)$ une droite donnée dans le plan et $A$ un point n'appartenant pas à $(D).$
On note $H$ le pied de la perpendiculaire à $(D)$ passant par $A$, et $A'$ le symétrique de $A$ par rapport à $H.$
Démontrer que pour tout point $M$ appartenant à $(D)$ tel que $M\neq H$, on a : $AH<AM$
Solution

$H$ est le point de $(D)$ le plus proche de $A$ donc, $AH$ est la distance de $A$ à la droite $(D).$
Démontrons que $AH<AM$ pour tout point $M\in(D)\ $ et $\ M\neq H.$
Comme $AMA'$ est un triangle alors, on a :
$AA'<AM+MA'\ $ (car $\ M\notin[AA'])$
Or, $\ AA'=AH+HA'$ donc, $AH+HA'<AM+MA'$
Par suite, $AH+AH<AM+MA'\ $ (car $\ HA'=AH)$
Ainsi, $2AH<AM+MA'$
Mais comme $AMA'$ est isocèle alors, $AM=MA'$
Ce qui donne :
$\begin{array}{rcrcl} 2AH<AM+MA&\Rightarrow&2AH&<&AM+AM\\ \\&\Rightarrow&2AH&<&2AM\\ \\&\Rightarrow&AH&<&AM\end{array}$
D'où, $\boxed{AH<AM}$
IV.2. Définition
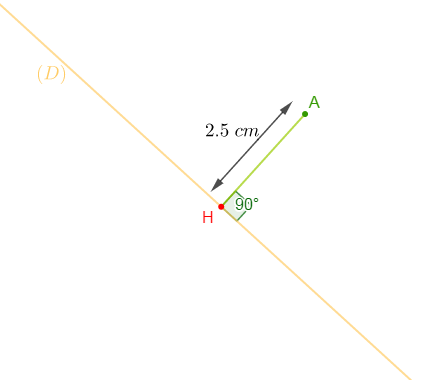
La distance d'un point $A$ à une droite $(D)$ est la longueur du segment de droite joignant $A$ au pied $H$ de la perpendiculaire à $(D)$ passant par $A.$
IV.3. Propriété
Soit $(D)$ une droite et $A$ un point du plan. Soit $H$ le pied de la perpendiculaire à $(D)$ passant par $A.$
Quelque soit le point $M\in(D)$ tel que $M\neq H$ on a :
$$AH<AM$$
Application 1
Tracer une droite $(D)$ et placer un point $A$ à $2.5\;cm$ de $(D).$
Solution

Application 2
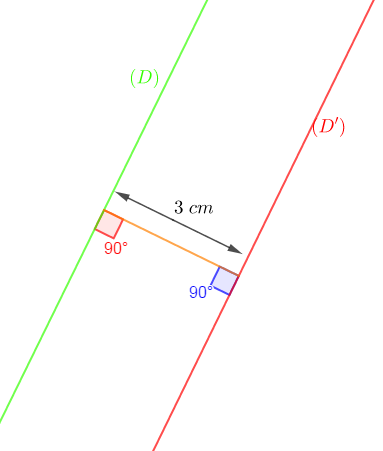
Tracer deux droites $(D)\ $ et $\ (D')$ distantes de $3\;cm$
Solution

V. Propriété de la bissectrice d'un angle
V.1. Activité
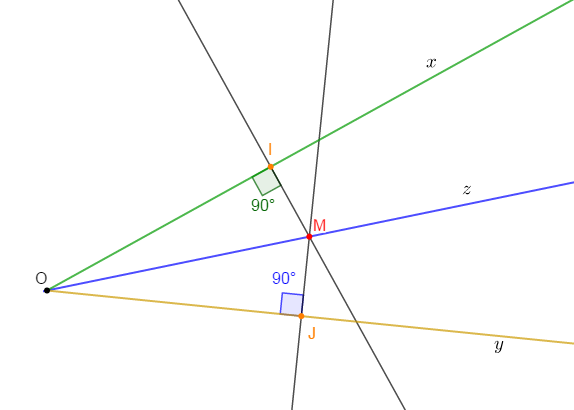
Tracer deux demi-droites $[Ox)\ $ et $\ [Oy).$
Tracer la bissectrice $[Oz)$ de l'angle $\widehat{xOy}$ puis y placer un point $M.$
Comparer la distance de $M$ à $[Ox)$ à celle de $M$ à $[Oy).$
Solution

$MI=MJ\;,\ M$ est équidistant des supports des côtés de l'angle.
V.2. Propriété
Si un point $M$ appartient à la bissectrice d'un angle alors, il est équidistant des supports des deux côtés de l'angle.
Auteur:
Mamadou Siradji Dia

Commentaires
OULIMATA DIEME (non vérifié)
lun, 01/18/2021 - 20:54
Permalien
MON OBJECTIF EST DE ETUDIERET DE REUSSIR POUR AIDER MES PARENTS
OULIMATA DIEME (non vérifié)
lun, 01/18/2021 - 20:54
Permalien
MON OBJECTIF EST DE ETUDIERET DE REUSSIR POUR AIDER MES PARENTS
Mr Sonko (non vérifié)
mer, 11/24/2021 - 10:48
Permalien
Contribution
Anonyme (non vérifié)
sam, 01/13/2024 - 19:18
Permalien
PDF
Ajouter un commentaire