Solution des exercices : Généralités sur le mouvement - 2nd S
Classe:
Seconde
Exercice 1
I. Dans chacun des cas suivants, choisissons la bonne réponse.
1) Dans le cas d'un mouvement rectiligne uniforme
a) le vecteur vitesse est constant.
2) Dans le cas d'un mouvement circulaire uniforme
b) la valeur du vecteur vitesse est constante.
3) Dans le cas d'un mouvement curviligne uniforme:
b) la valeur du vecteur vitesse est constante.
4) Lorsque la valeur du vecteur vitesse est constante
a. le mouvement est uniforme.
5) Lorsque le vecteur vitesse est constant
b) le mouvement est rectiligne uniforme.
II. Lorsqu'on éternue, on ferme les yeux involontairement. Le conducteur d'une automobile roulant à $108\;km.h^{-1}$ éternue pendant une demi-seconde.
Calculons la distance qu'il a parcouru sans voir la route.
Soit $d$ cette distance alors, on a : $$d=v.t$$
avec $t=\dfrac{1}{2}\;s=\dfrac{1}{2}\times\dfrac{1}{3600}\;h$
A.N : $d=108\times\dfrac{1}{7200}=0.015$
Donc, $\boxed{d=0.015\;km=15\;m}$
Exercice 2
On étudie la course d'Usain Bolt le Jamaïcain avec précision. On effectue un chronométrage tous les 10 mètres.
1) Complétons la colonne position
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|}\hline&M_{0}&M_{1}&M_{2}&M_{3}&M_{4}&M_{5}&M_{6}&M_{7}&M_{8}&M_{9}&M_{10}\\ \hline\text{Temps (s)}&0&1.85&2.91&3.82&4.70&5.51&6.37&7.19&8.01&8.87&9.72\\ \hline\text{Position (m)}&0&10&20&30&40&50&60&70&80&90&100\\ \hline\text{Vitesse}&&&&&&&&&&&\\ \text{instantanée}&-&6.9&10.2&11.2&11.8&11.98&11.90&12.2&11.9&11.7&-\\(m/s)&&&&&&&&&&&\\\hline\end{array}$$
2) Calculons les différentes vitesses instantanées. (Voir tableau)
3) Calculons la vitesse moyenne entre $M_{0}\ $ et $\ M_{3}$, puis entre $M_{4}\ $ et $\ M_{9}$
On a :
$\begin{array}{rcl} V_{_{M}}&=&\dfrac{M_{0}M_{3}}{t_{_{3}}-t_{_{0}}}\\ \\&=&\dfrac{30-0}{2.9-0}\\ \\&=&10.3\end{array}$
Ainsi, $\boxed{V_{_{M}}=10.3\;m.s^{-1}}$
$V_{_{M}}=\dfrac{M_{0}M_{3}}{t_{_{3}}-t_{_{0}}}$
De même on a :
$\begin{array}{rcl} V_{_{M'}}&=&\dfrac{M_{4}M_{9}}{t_{_{9}}-t_{_{4}}}\\ \\&=&\dfrac{90-40}{8.87-4.70}\\ \\&=&12\end{array}$
D'où, $\boxed{V_{_{M'}}=12\;m.s^{-1}}$
D'où, $\boxed{v_{2}=0.33\,m\cdot s^{-1}}$
Exercice 3
Un mobile autoporteur est lancé sur une table horizontale : On enregistre les positions successives d'un point $M$ du mobile.
Entre deux positions enregistrées, il s'est écoulé une durée $\Delta t=60\;ms.$
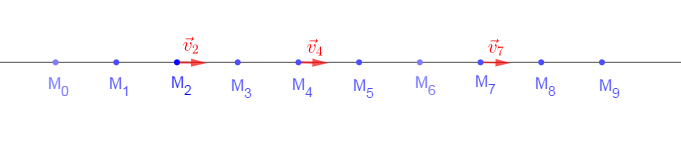
L'enregistrement de sa trajectoire est donnée par la figure ci-dessous :
$$\begin{array}{|cccccccccccc|}\hline&M_{0}&M_{1}&M_{2}&M_{3}&M_{4}&M_{5}&M_{6}&M_{7}&M_{8}&M_{9}\\&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\&t_{0}&t_{1}&t_{2}&t_{3}&t_{4}&t_{5}&t_{6}&t_{7}&t_{8}&t_{9}\\ \hline\end{array}$$
Échelle : $1\,cm$ sur le schéma représente $2\,cm$ en réalité
1) Nommons les points $M_{0}\;;\ M_{1}\;;\ M_{2}\;;\ \ldots\ (M_{0}$ étant le premier point de la trajectoire$).$
$M_{0}\;;\ M_{1}\;;\ M_{2}\;;\ \ldots M_{n}$ sont respectivement le premier, deuxième , troisième$\ldots$ $(n+1)^{ième}$ point de la trajectoire
2) La trajectoire du mobile est une droite
3) Nature du mouvement du mobile
Le mouvement est rectiligne uniforme car, la trajectoire est une droite et le mobile parcourt des distances égales pendant des durées égales
4) Calcul des vitesses instantanées du mobile aux dates $t_{2}\;,\ t_{4}\ $ et $\ t_{7}.$
$\begin{array}{rcl} v_{2}&=&\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}\\ \\&=&\dfrac{M_{1}M_{3}}{2\Delta t}\\ \\&=&\dfrac{4\cdot 10^{-2}}{2\times 60\cdot 10^{-3}}\\ \\&=&0.33\end{array}$
D'où, $\boxed{v_{2}=0.33\,m\cdot s^{-1}}$
$\begin{array}{rcl} v_{4}&=&\dfrac{M_{5}M_{3}}{t_{5}-t_{3}}\\ \\&=&\dfrac{M_{5}M_{3}}{2\Delta t}\\ \\&=&\dfrac{4\cdot 10^{-2}}{2\times 60\cdot 10^{-3}}\\ \\&=&0.33\end{array}$
Donc, $\boxed{v_{4}=0.33\,m\cdot s^{-1}}$
$\begin{array}{rcl} v_{7}&=&\dfrac{M_{8}M_{6}}{t_{8}-t_{6}}\\ \\&=&\dfrac{M_{8}M_{6}}{2\Delta t}\\ \\&=&\dfrac{4\cdot 10^{-2}}{2\times 60\cdot 10^{-3}}\\ \\&=&0.33\end{array}$
Ainsi, $\boxed{v_{7}=0.33\,m\cdot s^{-1}}$
5) Représentons le vecteur vitesse du mobile aux positions $M_{2}\;,\ M_{4}\ $ et $\ M_{7}.$

Échelle : $0.5\;cm\longrightarrow 0.33\;m\cdot s^{-1}$
6) On constate que le vecteur- vitesse instantanée est constant.
Le résultat est donc en accord avec la réponse de la 3e. question
7) La vitesse du mobile au point $M_{9}$
Le mouvement étant rectiligne uniforme alors, la vitesse est une constante d'où :
$$v_{9}=0.33\,m\cdot s^{-1}$$
$$v_{9}=0.33\,m\cdot s^{-1}$$
Exercice 4 : Mouvement d'un objet
On repère les positions successives d'un point $L$ d'un disque tournant autour d'un axe grâce à une lampe clignotante placée en $L$ et qui émet des éclairs à intervalles réguliers $\tau=20\;ms.$
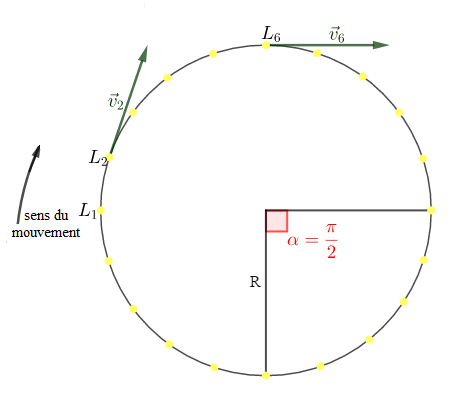
N.B : la courbe n'est pas à échelle. Cependant, entre deux éclairs on mesure $1.5\;cm$
1) Déterminons la vitesse instantanée de $L$ en $L_{6}\ $ et $\ L_{2}$
On a :
$\begin{array}{rcl} V_{_{6}}&=&\dfrac{L_{5}L_{7}}{t_{_{7}}-t_{_{5}}}\\ \\&=&\dfrac{L_{5}L_{7}}{2\tau}\\ \\&=&\dfrac{3.10^{-2}}{2\times 20.10^{-3}}\\ \\&=&0.75\end{array}$
D'où, $\boxed{V_{_{6}}=0.75\;m.s^{-1}}$
De même :
$\begin{array}{rcl} V_{_{2}}&=&\dfrac{L_{1}L_{3}}{t_{_{3}}-t_{_{1}}}\\ \\&=&\dfrac{L_{1}L_{3}}{2\tau}\\ \\&=&\dfrac{3.10^{-2}}{2\times 20.10^{-3}}\\ \\&=&0.75\end{array}$
Donc, $\boxed{V_{_{2}}=0.75\;m.s^{-1}}$
Traçons les vecteurs vitesses associés (Voir figure)
2) Calculons, sans utiliser la règle, la vitesse angulaire $(\omega)$ du solide.
Le mouvement est circulaire uniforme alors :
$\begin{array}{rcl}\omega=\dfrac{\alpha}{5\tau}&=&\dfrac{\dfrac{\pi}{2}}{5\times\tau}\\ \\&=&\dfrac{\pi}{2\times 5\times 20.10^{-3}}\\ \\&=&\dfrac{10^{3}\times\pi}{200}\\ \\&=&5\pi \end{array}$
Ainsi, $\boxed{\omega=15.7\;rad.s^{-1}}$
3) Vérifions la relation entre $V\ $ et $\ \omega$, la vitesse angulaire.
Par mesure, on trouve $R=5\;cm$
Par calcul, on a :
$\begin{array}{rcl} V=R\omega&\Rightarrow&R=\dfrac{V}{\omega}\\ \\&\Rightarrow&R=\dfrac{0.75}{15.7}\\ \\&\Rightarrow&R=4.8\;cm\end{array}$
Donc, aux erreurs expérimentales près, on trouve le même rayon.
4) En déduisons la période $T$ de rotation.
On a :
$\begin{array}{rcl}\omega=\dfrac{2\pi}{T}&\Rightarrow&T=\dfrac{2\pi}{\omega}\\ \\&\Rightarrow&T=\dfrac{2\pi}{5\pi}\\ \\&\Rightarrow&T=0.4\end{array}$
D'où, $\boxed{T=0.4\;s}$
5) Le vecteur vitesse de $L$ n'est pas constant au cours du temps, car il change de direction et de sens au cours du temps.
Exercice 5 : Étude du mouvement d'un enfant sur un tremplin
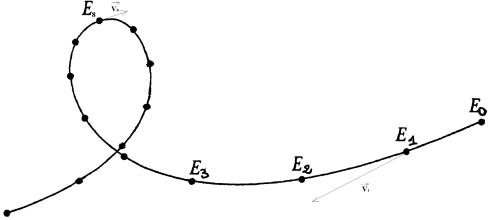
L'enregistrement ci-dessous représente dans le référentiel terrestre les positions $E_{i}$ d'un enfant en rollers sur un tremplin.
Ces positions sont inscrites à intervalles de temps égaux $\tau=0.20\;s$
1) Détermination des différentes phases du mouvement (uniforme, accéléré, décéléré).
$-\ $ De $E_{1}\ $ à $\ E_{2}$, le mouvement est accéléré car le mobile parcourt des distances de plus en plus grandes pour des durées égales.
$-\ $ De $E_{3}\ $ à $\ E_{10}$, le mouvement est décéléré car le mobile parcourt des distances de plus en plus petites pour des durées égales
$-\ $ De $E_{10}\ $ à $\ E_{12}$, le mouvement est uniforme car le mobile parcourt des distances égales pour des durées égales
$-\ $ De $E_{12}\ $ à $\ E_{14}$, le mouvement est accéléré
2) Détermination des valeurs de $v_{1}\ $ et $\ v_{8}$, vitesses instantanées du point $E$ aux instants $t_{1}\ $ et $\ t_{8}$
On a :
$\begin{array}{rcl} V_{_{1}}&=&\dfrac{E_{0}E_{2}}{t_{_{2}}-t_{_{0}}}\\ \\&=&\dfrac{E_{0}E_{2}}{2\tau}\\ \\&=&\dfrac{8\times 0.5}{2\times 0.20}\\ \\&=&10\end{array}$
Donc, $\boxed{V_{_{1}}=10\;m.s^{-1}}$
De même :
$\begin{array}{rcl} V_{_{8}}&=&\dfrac{E_{7}E_{9}}{t_{_{9}}-t_{_{7}}}\\ \\&=&\dfrac{E_{7}E_{9}}{2\tau}\\ \\&=&\dfrac{2.5\times 0.5}{2\times 0.20}\\ \\&=&3.125\end{array}$
D'où, $\boxed{V_{_{8}}=3.125\;m.s^{-1}}$
3) Représentation des vecteurs vitesse $\vec{v}_{1}\ $ et $\ \vec{v}_{8}$
Échelle : $1\;cm\longrightarrow 2\;m.s^{-1}$
Exercice 11
Un camion $M_{1}$ quitte une ville $A$ à $8\,h\;50\,min$ pour se rendre à une ville $B$ avec une vitesse constante $V_{1}=126\;km.h^{-1}$
Un autre camion $M_{2}$ quitte ville $B$ à $9\,h$ pour se rendre à la ville $A$ avec une vitesse $V_{2}$ inconnue. La route est supposée rectiligne et la distance entre les deux villes est de $259\;km.$

1) Calculons de la durée et la distance parcourue par $M_{1}$ avant le départ de $M_{2}.$
Soit $t=t_{2}-t_{1}$ avec $t_{1}$ la date de départ de $M_{1}\ $ et $\ t_{2}$ la date de départ du camion $M_{2}$
On a :
$\begin{array}{rcl} t&=&t_{2}-t_{1}\\ \\&=&9h-8\,h\;50\,mn\\ \\&=&=8\,h\;60\;mn-8\,h\;50\;mn\\ \\&=&10\,mn\end{array}$
D'où, $\boxed{t=10\,mn}$
Ainsi, au bout de $t=10\,mn$ le camion $M_{1}$ aura parcouru une distance $x_{0_{1}}=V_{1}.t$
Par suite :
$\begin{array}{rcl} x_{0_{1}}&=&V_{1}.t\\ \\&=&126\times\dfrac{10}{60}\\ \\&=&21\end{array}$
D'où, $\boxed{x_{0_{1}}=21\;km}$
2) En prenant comme origine des espaces $(x=0)$ la ville $A$ et comme origine des dates $(t=0)$ l'instant de départ du camion $M_{2}.$
2.1) Déterminons l'équation horaire $x_{1}$ du camion $M_{1}$
Soit : $x_{1}=V_{1}t+x_{0_{1}}\Rightarrow x_{1}=126t+21$
D'où, $\boxed{x_{1}(t)=126t+21}$
2.2) Détermination en fonction de $V_{2}$ l'équation horaire $x_{2}$ du camion $M_{2}.$
En tenant compte de l'orientation de l'axe, on a : $x_{2}=-V_{2}t+x_{0_{2}}$
Or, à $t=0\,s\;,\ x_{0_{2}}=259\,km$ donc, $x_{2}=-V_{2}t+259$
Ainsi, $\boxed{x_{2}(t)=-V_{2}t+259}$
3) Déterminons La date $t$ et l'heure d'arrivée $t'$ du camion $M_{1}$ à destination
L'équation horaire du camion $M_{1}$ étant donnée par : $x_{1}=126t+21$
Comme la distance entre les deux villes est de $259\;km$ alors, le camion $M_{1}$ arrive à destination lorsque $x_{1}=259.$
Par suite,
$\begin{array}{rcl} 126t+21=259&\Rightarrow&126t=259-21\\ \\&\Rightarrow&t=\dfrac{259-21}{126}\\ \\&\Rightarrow&t=1\,h\ 53\,mn\end{array}$
D'où, $\boxed{t=1\,h\ 53\,mn}$
Le camion $M_{1}$ ayant quitté la Ville $A$ vers $8\,h\ 50\,mn$ donc, l'heure d'arrivée $t'$ à destination sera donnée par :
$\begin{array}{rcl} t'&=&8\,h\ 50\,mn+t\\ \\&=&8\,h\ 50\,mn+1\,h\ 53\,mn\\ \\&=&10\,h\ 43\,mn\end{array}$
Ainsi, $\boxed{t'=10\,h\ 43\,mn}$
4) Déterminons la vitesse $V_{2}$ du camion $M_{2}$ pour que les deux mobiles arrivent en même temps à destination
Soit $t''$ le temps mis par le camion $M_{2}$ pour arriver à destination.
L'heure d'arrivée étant égale $t'=10\,h\ 43\,mn$ alors,
$\begin{array}{rcl} t''&=&10\,h\ 43\,mn-9\,h\\ \\&=&1\,h\ 43\,mn\end{array}$
Par ailleurs, d'après l'équation horaire du camion $M_{2}$, on a : $x_{2}=-V_{2}t+259$
Or, le camion $M_{2}$ arrive à destination lorsque $x_{2}=0$
Par suite,
$\begin{array}{rcl} -V_{2}.t''+259=0&\Rightarrow&V_{2}=\dfrac{259}{t''}\\\\&\Rightarrow&V_{2}=\dfrac{259}{\left(1+\dfrac{43}{60}\right)}\\\\&\Rightarrow&V_{2} =150.87\;km\cdot h^{-1}\end{array}$
D'où, $\boxed{V_{2}=150.87\;km\cdot h^{-1}}$
5) En supposant que $V_{2}=238\;m.s^{-1}$, en déduisons :
5.1) La date et l'heure de rencontre des deux camions.
Soit : $V_{2}=238\;m\cdot s^{-1}$, ce qui donne, après conversion :
$V_{2}=238\times 3.6=856.8\;km\cdot h^{-1}$
L'équation horaire sera alors donnée par :
$x_{2}=-856.8t+259$
A la rencontre, on a : $x_{1}=x_{2}$
Ainsi,
$\begin{array}{rcl} 126t+21=-856.8t+259&\Rightarrow&126t+856.8t=259-21\\\\&\Rightarrow&982.8t=238\\\\&\Rightarrow&t=\dfrac{238}{982.8}\\\\&\Rightarrow&t =14.5\,mn\end{array}$
D'où, $\boxed{t=14\,mn\ 30\,s}$
L'origine des dates $(t=0)$ étant l'instant de départ du camion $M_{2}$ donc, l'heure de rencontre $t'$ est donnée par
$t'=9\,h+14\,mn\ 30\,s=9h\ 14\,mn\ 30\,s$
D'où, $\boxed{t'=9h\ 14\,mn\ 30\,s}$
5.2) La position de rencontre.
Soit $d$ la position de rencontre des deux camions.
Considérons l'équation horaire du camion $M_{2}\ : x_{2}=-856.8t+259$
On obtient alors : $d=-856.8\times\dfrac{14.5}{60}+259=51.9\,km$
D'où, $\boxed{d=51.9\,km}$
6) Déterminons les dates où les deux camions sont distants de $5\;km$
Les deux camions sont distants de $5\;km$ signifie que $\left|x_{2}-x_{1}\right|=5$
On a :
$\begin{array}{rcl} \left|x_{2}-x_{1}\right|=5&\Leftrightarrow&\left|-856.8t+259-(126t+21)\right|=5\\\\&\Leftrightarrow&\left|-982.8t+238\right|=5\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}-982.8t+238&=&5\\-982.8t+238&=&-5 \end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl}-982.8t&=&-233\\-982.8t&=&-243 \end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} t&=&\dfrac{233}{982.8}\\\\t&=&\dfrac{243}{982.8}\end{array}\right.\nonumber\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} t_{1}&=&14\,mn\ 12\,s\\t_{2}&=&14\,mn\ 48\,s\end{array}\right.\end{array}$
Commentons le résultat
La date $t_{1}$ correspond à la date avant la rencontre
La date $t_{2}$ correspond à la date après la rencontre
Exercice 12

1. Nature précise du mouvement
Le mouvement est uniformément accéléré, car le mobile parcourt des distances de plus en plus grandes pour des durées égales
2-1. Mesure de la distance $M_{0}M_{8}$
$M_{0}M_{8}=23\,cm$
2.2 Déterminons l'intervalle de temps qui sépare les deux positions $M_{0}$ et $M_{8}$
$\begin{array}{rcl} t&=&40\,m\cdot s\Delta t\\&=&8 t\\&=&8\times40\,m\cdot s\\\Rightarrow\Delta \boxed{t=3.2\cdot 10^{-1}s} \end{array}$
2.3 Déterminons les valeurs des vitesses instantanées $v_{1}$, $v_2$ et $v_5.$
$\begin{array}{rcl} v_{1}&=&\dfrac{M_{0}M_{2}}{t_{2}-t_{0}}\\&=&\dfrac{M_{0}M_{2}}{2t}\\&=&\dfrac{1.5\cdot10^{-2}}{2\times40\cdot10^{-3}}\\\Rightarrow\boxed{v_{1}=0.19m\cdot s^{-1}} \end{array}$
$\begin{array}{rcl} v_{2}&=&\dfrac{M_{1}M_{3}}{t_{3}-t_{1}}\\&=&\dfrac{M_{1}M_{3}}{2t}\\&=&\dfrac{3\cdot 10^{-2}}{2\times40\cdot^{-3}}\\\Rightarrow\boxed{v_{2}=0.38m\cdot s^{-1}} \end{array}$
$\begin{array}{rcl} v_{5}&=&\dfrac{M_{4}M_{6}}{t_{6}-t_{4}}\\&=&\dfrac{M_{4}M_{6}}{2t}\\&=&\dfrac{7\cdot10^{-2}}{2\times40\cdot10^{-3}}\\\Rightarrow\boxed{v_{2}=0.88m\cdot s^{-1}} \end{array}$
3.2. Les vitesses instantanées augmentent avec le temps.
L'observation des vitesses instantanées successives permet donc d'affirmer que le mouvement du mobile autoporteur est accéléré
3.3. Représentons les vecteurs vitesses instantanées correspondant aux positions $M_{2}$ et $M_{5}$ du mobile
(Voir figure)
Exercice 13
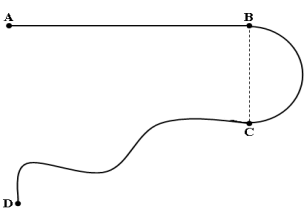
1. Complétons le tableau
$\begin{array}{|l|c|c|} \hline \text{Partie du trajet }&\text{Nature de la trajectoire }&\text{Nature du mouvement}\\ \hline AB&\text{Droite }&\text{Rectiligne }\\ \hline BC&\text{Arc de cercle }&\text{Circulaire }\\ \hline CD&\text{Courbe }&\text{Curviligne}\\ \hline \end{array}$
2.a. Détermination de sa vitesse moyenne $V_{1}$ sur le trajet $AB.$
$\begin{array}{rcl} V_{1}&=&\dfrac{AB}{\Delta t_{1}}\\&=&\dfrac{340}{20}\\\Rightarrow\boxed{V_{1}=17\,m\cdot s^{-1}} \end{array}$
b. Détermination de la distance du parcours $BC.$
$\begin{array}{rcl} BC&=&V_{2}\Delta t_{2}\\&=&15.7\times30\\\Rightarrow\;\boxed{BC=471\,m} \end{array}$
c. Détermination de la durée $\Delta t_{3}$ de ce parcours $CD$
$\begin{array}{rcl} \Delta t_{3}&=&\dfrac{CD}{V_{3}}\\&=&\dfrac{143}{14.3}\\\Rightarrow\Delta\boxed{t_{3}=10s} \end{array}$
3) Déduisons la nature du mouvement du mobile sur tout le trajet entre $A$ et $D$
Le mouvement du mobile sur tout le trajet est curviligne, puisque la trajectoire est une courbe
4. Calcul de la vitesse moyenne $V_{m}$ du mobile sur tout le trajet entre $A$ et $D.$
$\begin{array}{rcl} V_{m}&=&\dfrac{AB+BC+CD}{\Delta t_{1}+\Delta t_{2}+\Delta t_{3}}\\&=&\dfrac{340+471+143}{20+30+10}\\\Rightarrow\boxed{V_{m}=15.9\,m\cdot s^{-1}} \end{array}$
Exercice 14
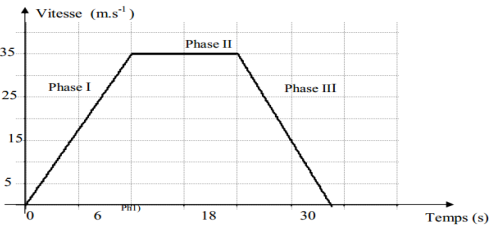
1. Étude de la phase $I$
a. Rappel de la définition de la trajectoire d'un mobile.
La trajectoire d'un mobile est l'ensemble des positions successivement occupées par le mobile au cours du temps
b. La vitesse du véhicule de $0$ à $12$ secondes augmente , la vitesse est une fonction croissante du temps
c. Déduction de la nature du mouvement du véhicule
Le mouvement est accéléré
2) Étude la phase $II$
a. La vitesse du véhicule pendant cette phase est constante
b. Détermination, à partir du graphique, la vitesse du véhicule et la durée de la phase $II.$
$V_{II}=35\,m\cdot s^{-1}$
c.Convertissons la vitesse du véhicule pendant cette phase en $km\cdot h^{-1}.$
$\begin{array}{rcl} V_{II}&=&35\,m\cdot s^{-1}\\&=&35\times\dfrac{m}{s}\\&=&35\times\dfrac{10^{3}km}{\dfrac{1}{3600}h}\\\Rightarrow\boxed{V_{II}=126\,km\cdot h^{-1}} \end{array}$
d. Calcul de la distance d parcourue par le véhicule au cours de cette phase.
$\begin{array}{rcl} d_{II}&=&V_{II}\Delta t_{II}\\&=&126\times(24-12)\\\Rightarrow\boxed{d_{II}=1512\,km} \end{array}$
3. Étude de la phase $III$
a. La vitesse du véhicule pendant cette phase diminue , car cette vitesse est une fonction décroissante du temps
b. Nature de mouvement du véhicule au cours de cette phase
Le mouvement du véhicule est retardée ou décéléré
c.Détermination, à partir du graphique, la vitesse en $m\cdot s^{-1}$ du véhicule au temps $t=30\text{secondes}$
$V_{III}=15\,m\cdot s^{-1}$

Commentaires
Salymata (non vérifié)
sam, 09/12/2020 - 02:27
Permalien
s'il vous proposez une
Sokhna (non vérifié)
sam, 11/07/2020 - 11:52
Permalien
Ton numéro
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Ali gawe (non vérifié)
jeu, 08/22/2024 - 21:48
Permalien
Correction de l'exercice 10
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Astou diouf (non vérifié)
dim, 11/12/2023 - 13:09
Permalien
Correction exercice 10svpppp
Mama Demba (non vérifié)
jeu, 11/21/2024 - 17:29
Permalien
Élève
Amadou Diallo (non vérifié)
sam, 01/07/2023 - 19:07
Permalien
D'étudier
Demba Diaks (non vérifié)
lun, 11/06/2023 - 06:48
Permalien
Élève
Amadou Diallo (non vérifié)
ven, 11/15/2024 - 20:54
Permalien
Détails exo 11
Marie Kanté (non vérifié)
ven, 12/04/2020 - 23:46
Permalien
S
Fatim ba (non vérifié)
ven, 12/01/2023 - 18:59
Permalien
S
Fatim ba (non vérifié)
ven, 12/01/2023 - 18:59
Permalien
S
goor yombul (non vérifié)
dim, 12/06/2020 - 03:20
Permalien
demande de correction
Anonyme (non vérifié)
dim, 12/13/2020 - 07:28
Permalien
Super pour les corrections
morel (non vérifié)
mer, 09/28/2022 - 18:42
Permalien
exercice10 la correction svp
Cheikh tidiane DIENE (non vérifié)
ven, 12/25/2020 - 14:09
Permalien
Demande d'aide
Mbéne séne (non vérifié)
mer, 01/03/2024 - 23:16
Permalien
Aider moi sur l'exercice 11
Cheikh tidiane DIENE (non vérifié)
ven, 12/25/2020 - 14:09
Permalien
Demande d'aide
Anonyme (non vérifié)
sam, 01/02/2021 - 15:29
Permalien
S'il vous plait aider moi sur
fcherif
sam, 01/02/2021 - 16:27
Permalien
T'inquiète on va mettre la
T'inquiète on va mettre la correction
sokhna_jarrah (non vérifié)
sam, 01/09/2021 - 23:52
Permalien
Rectification
Christian
mer, 10/23/2024 - 00:01
Permalien
Ma pensée sur le site
Lamine kiang (non vérifié)
lun, 01/11/2021 - 21:46
Permalien
Exo 4
Youssou (non vérifié)
mar, 01/12/2021 - 17:44
Permalien
Demande d'aide technique
Talla niang (non vérifié)
mar, 01/19/2021 - 18:48
Permalien
Franchement c'est super !
Khady (non vérifié)
lun, 10/21/2024 - 20:54
Permalien
Élèves
Muyi (non vérifié)
jeu, 10/24/2024 - 20:29
Permalien
Frbjh
Talla niang (non vérifié)
mar, 01/19/2021 - 18:49
Permalien
Franchement c'est super !
Mamadou wade (non vérifié)
lun, 01/25/2021 - 02:26
Permalien
Eleve.
Anonyme (non vérifié)
mer, 03/03/2021 - 16:42
Permalien
Merci pour l'aide
salihou Ramadan (non vérifié)
dim, 03/14/2021 - 23:48
Permalien
document
Loi (non vérifié)
lun, 10/25/2021 - 03:43
Permalien
Exercice 6
أماء (non vérifié)
ven, 12/29/2023 - 21:09
Permalien
لم أجد إجابة التمرين 6
Anonyme (non vérifié)
ven, 12/10/2021 - 00:10
Permalien
il n'y a que les équations
Anonyme (non vérifié)
dim, 12/19/2021 - 14:31
Permalien
4.10-2 vient dou?
Anonyme (non vérifié)
ven, 03/18/2022 - 06:34
Permalien
C'est tellement magnifique et
Ségolène mendy (non vérifié)
mer, 05/11/2022 - 21:39
Permalien
Est ce que je peux avoir la
Anonyme (non vérifié)
mer, 08/17/2022 - 14:29
Permalien
Il faut répondre aux
Al-annaf Mahamat (non vérifié)
mer, 10/19/2022 - 06:57
Permalien
S'il vous plaît aider moi sur
Mamadou Diallo (non vérifié)
sam, 11/23/2024 - 14:55
Permalien
Exo 3
Pages
Ajouter un commentaire