Solution des exercices : Le cercle 6e
Classe:
Sixième
Exercice 1
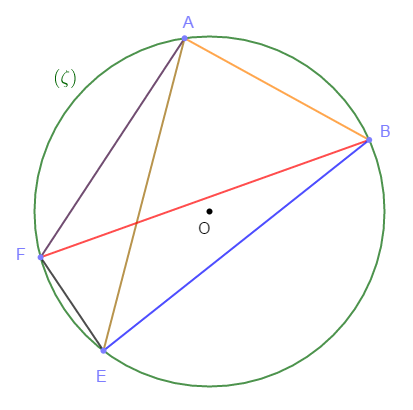
Soit $(\zeta)$ un cercle de centre de centre $O$ et de rayon $3.5\,cm.$
1) Marquons quatre points $A\;;\ B\;;\ E$ et $F$ sur ce cercle.
2) On obtient six $(6)$ cordes reliant deux à deux les quatre points marqués :
$$[AB]\;,\ [AE]\;,\ [AF]\;,\ [BE]\;,\ [BF]\;,\ [EF]$$
Exercice 2
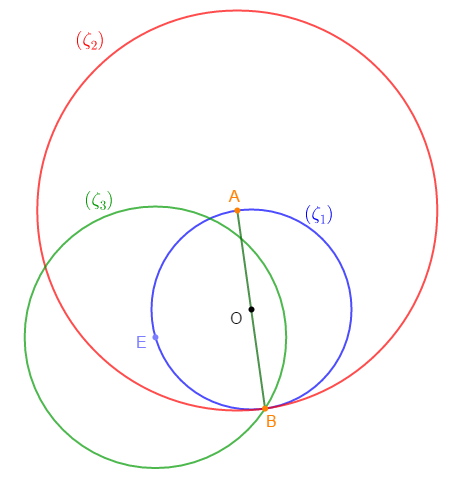
1) Marquons un point $O$ et traçons le cercle $(\zeta_{1})$ de centre $O$ et de rayon $2\,cm.$
2) a) Traçons un diamètre $[AB]$ de ce cercle puis, traçons le cercle $(\zeta_{2})$ de centre $A$ et dont un des rayons est le segment $[AB].$
b) $(\zeta_{1})\ $ et $\ (\zeta_{2})$ sont tangents intérieurement.
3) a) Marquons un point $E$ sur le cercle $(\zeta_{1})$ et traçons le cercle $(\zeta_{3})$ de centre $E$ et passant par $B.$
b) $(\zeta_{1})\ $ et $\ (\zeta_{3})$ sont sécants.
Exercice 3
1) Construisons une demi-droite oblique $[Ox).$
2) Marquons les points $A\;;\ B$ et $C$ dans cet ordre tel que :
$$OA=3\,cm\;;\ AB=3\,cm\quad\text{et}\quad BC=2\,cm$$
3) a) Calculons les distances $OB\ $ et $\ AC.$
On a :
$\begin{array}{rcl} OB&=&OA+AB\\ \\&=&3\,cm+3\,cm\\ \\&=&6\,cm\end{array}$
Donc, $\boxed{OB=6\,cm}$
$\begin{array}{rcl} AC&=&AB+BC\\ \\&=&3\,cm+2\,cm\\ \\&=&5\,cm\end{array}$
D'où, $\boxed{AC=5\,cm}$
b) Le point $A$ est le milieu du segment $[OB]$
En effet, $O\;,\ A\ $ et $\ B$ sont trois points alignés dans cet ordre tels que $OA=AB$ donc, $A$ est milieu de $[OB].$
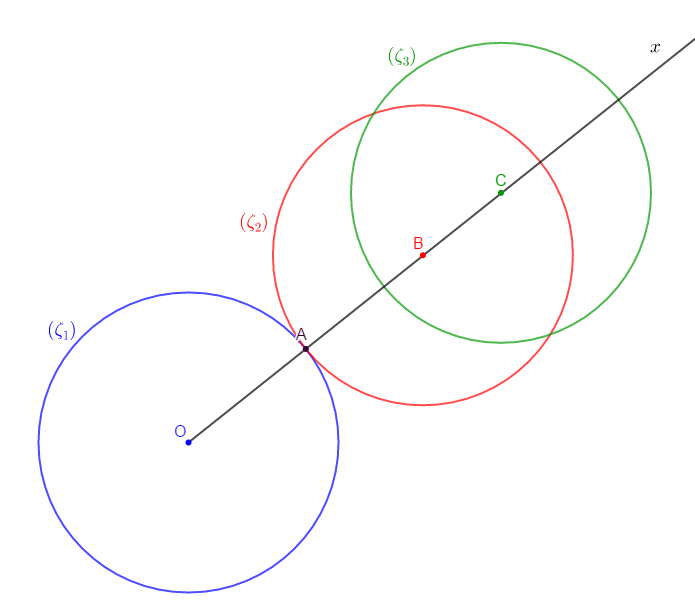
4) Construisons les cercles : $(\zeta_{2})\;;\ (\zeta_{2})\ $ et $\ (\zeta_{3})$ tels que :
$$\zeta_{1}(O\;;\ 3\;cm)\;,\ \zeta_{2}(B\;;\ 3\;cm)\quad\text{et}\quad\zeta_{2}(C\;;\ 3\;cm)$$
5) Déterminons les positions relatives des cercles : $(\zeta_{1})\ $ et $\ (\zeta_{2})$, $\ (\zeta_{2})\ $ et $\ (\zeta_{3})$, $\ (\zeta_{1})\ $ et $\ (\zeta_{3})$
On a :
$(\zeta_{1})\ $ et $\ (\zeta_{2})$ sont tangents extérieurement.
$(\zeta_{2})\ $ et $\ (\zeta_{3})$ sont sécants
$(\zeta_{1})\ $ et $\ (\zeta_{3})$ sont disjoints
Exercice 4
Soit $A\;,\ B\ $ et $\ C$ trois points alignés tels que : $AB=5\;cm\ $ et $\ BC=3\;cm.$
1) On peut marquer deux points $C$
Le point $C$ peut être placé à l'intérieur ou à l'extérieur du segment $[AB]$ tel que $BC=3\;cm$
2) Dans chaque cas, traçons les cercles de diamètre $[AC].$
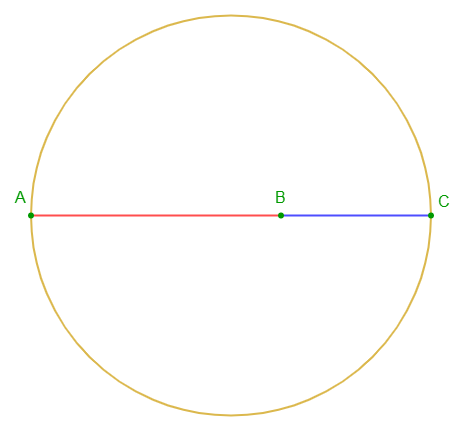
Lorsque le point est à l'intérieur du segment $[AB]$, on obtient la figure ci-dessous :
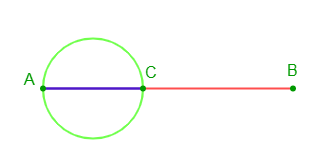
Lorsque le point est à l'extérieur du segment $[AB]$, on obtient la figure suivante :
Exercice 5
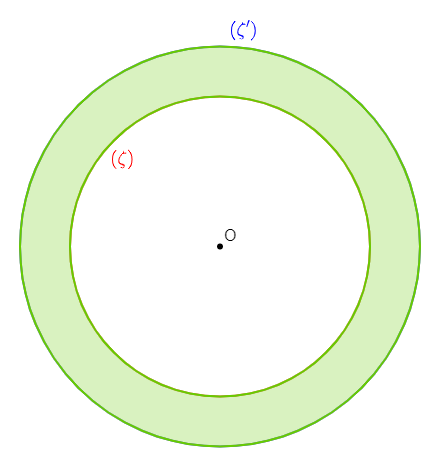
1) a) Construisons deux cercles $\zeta\ $ et $\ \zeta'$ tels que : $\zeta(O\;;\ 3\;cm)\ $ et $\ \zeta'(O\;;\ 4\;cm).$
b) Les cercles $\zeta\ $ et $\ \zeta'$ sont disjoints intérieurement.
En observant la figure, on remarque que les deux cercles n'ont aucun point en commun et le cercle $\zeta$ est situé à l'intérieur du cercle $\zeta'.$
Donc, les cercles $\zeta\ $ et $\ \zeta'$ sont disjoints intérieurement.
On remarque aussi que ces deux cercles ont le même centre $O.$
On dit alors que les cercles $\zeta\ $ et $\ \zeta'$ sont concentriques.
2) Calculons la valeur exacte des périmètres de $\zeta\ $ et $\ \zeta'.$
Le périmètre $\mathcal{P}$ d'un cercle de rayon $r$ est donné par :
$$\mathcal{P}=2\times\pi\times r$$
On choisit $\pi=3.2$
$-\ $ Pour le cercle $\zeta$, on a :
$\begin{array}{rcl}\mathcal{P}&=&2\times\pi\times r\\\\&=&2\times 3.2\times 3\\\\&=&19.2\end{array}$
Donc, $\boxed{\text{Périmètre de }\zeta=19.2\;cm}$
$-\ $ Pour le cercle $\zeta'$, on a :
$\begin{array}{rcl}\mathcal{P}&=&2\times\pi\times r\\\\&=&2\times 3.2\times 4\\\\&=&25.6\end{array}$
Donc, $\boxed{\text{Périmètre de }\zeta'=25.6\;cm}$
3) a) Calculons l'aire de $\zeta\ $ et $\ \zeta'\;;\ (\pi=3.2)$
L'aire $\mathcal{A}$ de la partie intérieure d'un cercle de rayon $r$ est donnée par :
$$\mathcal{A}=r\times r\times\pi$$
$-\ $ Pour le cercle $\zeta$, on a :
$\begin{array}{rcl}\mathcal{A}&=&r\times r\times\pi\\\\&=&3\times 3\times 3.2\\\\&=&28.8\end{array}$
Donc, $\boxed{\text{Aire de }\zeta=28.8\;cm^{2}}$
$-\ $ Pour le cercle $\zeta'$, on a :
$\begin{array}{rcl}\mathcal{A}&=&r\times r\times\pi\\\\&=&4\times 4\times 3.2\\\\&=&51.2\end{array}$
Donc, $\boxed{\text{Aire de }\zeta'=51.2\;cm^{2}}$
b) En déduisons l'aire de la couronne formés par les cercles $\zeta\ $ et $\ \zeta'.$
L'aire de la couronne formés par les cercles $\zeta\ $ et $\ \zeta'$ est donnée par :
$$\text{Aire de la couronne}=\text{Aire de }\zeta'-\text{Aire de }\zeta$$
En remplaçant $\text{Aire de }\zeta'\ $ et $\ \text{Aire de }\zeta$ par leur valeur, on obtient :
$\begin{array}{rcl}\text{Aire de la couronne}&=&\text{Aire de }\zeta'-\text{Aire de }\zeta\\\\&=&51.2-28.8\\\\&=&22.4\end{array}$
D'où, $\boxed{\text{Aire de la couronne}=22.4\;cm^{2}}$
Exercice 6
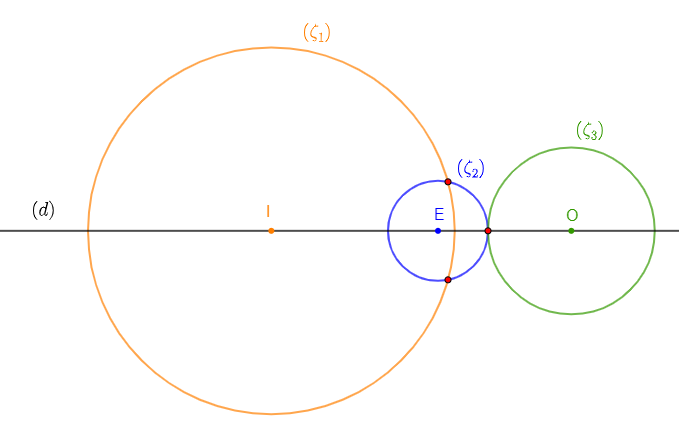
1) Plaçons les points $I\;,\ E\ $ et $\ O$ dans cet ordre sur une droite $(d)$ oblique tels que : $IE=5\;cm\ $ et $\ EO=4\;cm$
2) Construisons $\zeta_{1}(I\;;\ 5.5\;cm)\;;\ \zeta_{2}(E\;;\ 1.5\;cm)\;;\ \zeta_{3}(O\;;\ 2.5\;cm).$
3) Les cercles $(\zeta_{1})\ $ et $\ (\zeta_{2})$ sont sécants.
Justifions.
En observant la figure, on constate que $(\zeta_{1})\ $ et $\ (\zeta_{2})$ ont deux points en communs.
Par conséquent, $(\zeta_{1})\ $ et $\ (\zeta_{2})$ sont sécants.
4) Les cercles $(\zeta_{2})\ $ et $\ (\zeta_{3})$ sont tangents extérieurement.
Justifions.
En observant la figure, on remarque que $(\zeta_{2})\ $ et $\ (\zeta_{3})$ ont un seul point en commun et que ces deux cercles sont situés de part et d'autre de ce point commun.
Donc, $(\zeta_{2})\ $ et $\ (\zeta_{3})$ sont tangents extérieurement.
5) Les cercles $(\zeta_{1})\ $ et $\ (\zeta_{3})$ sont disjoints extérieurement.
Justifions.
En observant la figure, on remarque que $(\zeta_{1})\ $ et $\ (\zeta_{3})$ n'ont aucun point en commun.
On constate aussi que ces deux cercles sont situés de part et d'autre de l'espace qui les sépare.
Par conséquent, $(\zeta_{1})\ $ et $\ (\zeta_{3})$ sont sont disjoints extérieurement.
Exercice 7
1) Un cercle a un périmètre de $15\;cm.$
Calculons le rayon $r$ et le diamètre $D$ de ce cercle si $\pi=3.$
$-\ $ Calcul du rayon $r$ de ce cercle
On sait que le périmètre $\mathcal{P}$ d'un cercle de rayon $r$ est donné par :
$$\mathcal{P}=2\times\pi\times r$$
Ce qui donne alors : $r=\dfrac{\mathcal{P}}{2\times\pi}$
En remplaçant $\mathcal{P}\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl} r&=&\dfrac{\mathcal{P}}{2\times\pi}\\\\&=&\dfrac{15}{2\times 3}\\\\&=&\dfrac{15}{6}\\\\&=&2.5\end{array}$
D'où, $\boxed{r=2.5\;cm}$
$-\ $ Calcul du diamètre $D$ de ce cercle
Le diamètre $D$ de ce cercle est égal au double du rayon.
Donc, on a :
$$D=2\times r$$
En remplaçant $r$ par sa valeur, on obtient :
$\begin{array}{rcl} D&=&2\times r\\\\&=&2\times 2.5\\\\&=&5\end{array}$
D'où, $\boxed{D=5\;cm}$
2) Un disque a une aire de $75\;cm^{2}.$
Calculons le rayon $r$ et le diamètre $D$ correspondant à ce disque si $\pi=3.$
$-\ $ Calcul du rayon $r$ de ce disque
On sait que l'aire $\mathcal{A}$ d'un disque de rayon $r$ est donnée par :
$$\mathcal{A}=r\times r\times\pi=r^{2}\times\pi$$
Ce qui donne alors : $r^{2}=\dfrac{\mathcal{A}}{\pi}$
En remplaçant $\mathcal{A}\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl} r^{2}&=&\dfrac{\mathcal{A}}{\pi}\\\\&=&\dfrac{75}{3}\\\\&=&25\end{array}$
Donc, on trouve $r^{2}=25$
Comme $25=5^{2}$ alors, on a : $r^{2}=5^{2}$
D'où, $\boxed{\mathcal{r}=5\;cm}$
$-\ $ Calcul du diamètre $D$ de ce disque
Le diamètre $D$ de ce disque est égal au double du rayon.
Donc, on a :
$$D=2\times r$$
En remplaçant $r$ par sa valeur, on obtient :
$\begin{array}{rcl} D&=&2\times r\\\\&=&2\times 5\\\\&=&10\end{array}$
D'où, $\boxed{D=10\;cm}$
Exercice 8
1) Traçons $[AB]$ tel que : $AB=3\;cm.$
2) a) Traçons le cercle $(\zeta)$ dont $[AB]$ est un diamètre.
Pour cela, on trace le cercle de centre $O$ milieu de $[AB].$
b) Traçons le cercle $(\zeta')$ dont $[AB]$ est un rayon.
Pour cela, on trace le cercle de centre $A$ et passant par le point $B.$
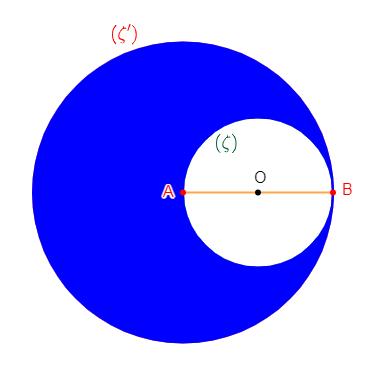
c) Les cercles $(\zeta)\ $ et $\ (\zeta')$ sont tangents intérieurement.
En observant la figure, on remarque que $(\zeta)\ $ et $\ (\zeta')$ ont un seul point en commun ; le point $B$ et que $(\zeta)$ est situé à l'intérieur de $(\zeta').$
Donc, les cercles $(\zeta)\ $ et $\ (\zeta')$ sont tangents intérieurement.
3) a) Calculons le périmètre de $(\zeta)\;\ (\pi=3.2)$
On sait que le périmètre $\mathcal{P}$ d'un cercle de diamètre $D$ est donné par :
$$\mathcal{P}=D\times\pi$$
En remplaçant $D\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl}\mathcal{P}&=&D\times\pi\\\\&=&3\times 3.2\\\\&=&9.6\end{array}$
D'où, $\boxed{\mathcal{P}=9.6\;cm}$
b) Calculons le périmètre de $\zeta'\;\ (\pi=3.1).$
On sait que le périmètre $\mathcal{P}$ d'un cercle de rayon $r$ est donné par :
$$\mathcal{P}=2\times\pi\times r$$
En remplaçant $r\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl}\mathcal{P}&=&2\times\pi\times r\\\\&=&2\times 3.1\times 3\\\\&=&18.6\end{array}$
D'où, $\boxed{\mathcal{P}=18.6\;cm}$
4) Colorions en bleu puis, déterminons l'aire formée par le disque intérieur de $(\zeta')$ et extérieur de $(\zeta)\;\ (\pi=3).$
On calcule d'abord l'aire $\mathcal{A}_{1}$ de la partie intérieure du cercle $(\zeta)$ puis, l'aire $\mathcal{A}_{2}$ de la partie intérieure du cercle $(\zeta').$
Ensuite, l'aire de la couronne formée par le disque intérieur de $(\zeta')$ et extérieur de $(\zeta)$ est donnée par :
$$\text{Aire de la couronne}=\text{Aire de }\zeta'-\text{Aire de }\zeta=\mathcal{A}_{2}-\mathcal{A}_{1}$$
$-\ $ Calcul de l'aire $\mathcal{A}_{1}$
On sait que l'aire $\mathcal{A}_{1}$ de la partie intérieure du cercle $(\zeta)$ de rayon $r$ est donnée par :
$$\mathcal{A}_{1}=r\times r\times\pi$$
Or, le rayon $r$ du cercle $\zeta$ est donné par :
$r=\dfrac{AB}{2}=\dfrac{3}{2}=1.5\;cm$
Donc, en remplaçant $r\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl}\mathcal{A}_{1}&=&r\times r\times\pi\\\\&=&1.5\times 1.5\times 3\\\\&=&6.75\end{array}$
D'où, $\boxed{\mathcal{A}_{1}=6.75\;cm^{2}}$
$-\ $ Calcul de l'aire $\mathcal{A}_{2}$
On sait que l'aire $\mathcal{A}_{1}$ de la partie intérieure du cercle $\zeta'$ de rayon $r$ est donnée par :
$$\mathcal{A}_{2}=r\times r\times\pi$$
Or, le rayon $r$ du cercle $\zeta'$ est égal à $AB=3\;cm$
Donc, en remplaçant $r\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl}\mathcal{A}_{2}&=&r\times r\times\pi\\\\&=&3\times 3\times 3\\\\&=&27\end{array}$
Ainsi, $\boxed{\mathcal{A}_{2}=27\;cm^{2}}$
$-\ $ Calcul de l'aire de la couronne
L'aire de la couronne formée par le disque intérieur de $(\zeta')$ et extérieur de $(\zeta)$ est alors donnée par :
$\begin{array}{rcl}\text{Aire de la couronne}&=&\mathcal{A}_{2}-\mathcal{A}_{1}\\\\&=&27-6.75\\\\&=&20.25\end{array}$
D'où, $\boxed{\text{Aire de la couronne}=20.25\;cm^{2}}$
Exercice 9
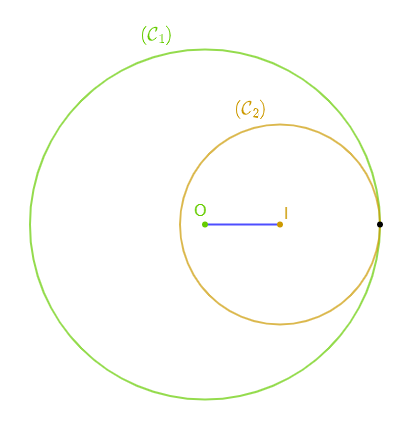
1) Traçons un cercle $\mathcal{C}_{1}$ de centre $O$ et diamètre $7\;cm.$
2) Marquons un point $I$ intérieur à $\mathcal{C}_{1}$ tel que $OI=1.5\;cm$
3) Construisons le cercle $\mathcal{C}_{2}(I\;;\ 2\;cm).$
4) Ces deux cercles sont tangents intérieurement.
En observant la figure, on remarque que $(\mathcal{C}_{1})\ $ et $\ (\mathcal{C}_{2})$ ont un seul point en commun et que $(\mathcal{C}_{2})$ est situé à l'intérieur de $(\mathcal{C}_{1}).$
Par conséquent, les cercles $(\mathcal{C}_{1})\ $ et $\ (\mathcal{C}_{2})$ sont tangents intérieurement.
5) a) Donnons la valeur exacte du périmètre de $\mathcal{C}_{1}.$
Le périmètre $\mathcal{P}$ du cercle $\mathcal{C}_{1}$ de diamètre $D=7\;cm$ est donné par :
$$\mathcal{P}=D\times\pi$$
En remplaçant $D\ $ et $\ \pi$ par leur valeur, on obtient :
$\begin{array}{rcl}\mathcal{P}&=&D\times\pi\\\\&=&7\times 3.1\\\\&=&21.7\end{array}$
D'où, $\boxed{\mathcal{P}=21.7\;cm}$
b) Donnons une valeur approchée du périmètre du cercle $\mathcal{C}_{1}\;\ (\pi=3.1).$
On remarque que $21.7$ est proche de $22.$
Donc, le périmètre du cercle $\mathcal{C}_{1}$ est approximativement égal à $22\;cm$
Exercice 10
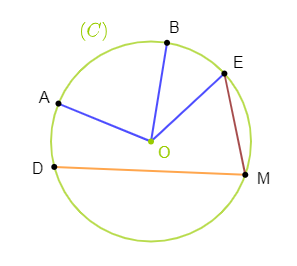
1) Traçons un cercle $(C)$ de centre $O$ et de rayon $2\;cm.$
2) Plaçons les points $A\;,\ B\;,\ E\;,\ M\ $ et $\ D$ sur ce cercle.
3) Indiquons trois rayons et traçons deux cordes.
On sait que : le rayon est la distance entre le centre du cercle et un point du cercle.
Donc, $OA\;;\ OB\ $ et $\ OE$ sont trois rayons de ce cercle.
On sait que : une corde est un segment dont les extrémités sont sur le cercle.
Donc, $[ME]\ $ et $\ [MD]$ sont deux cordes du cercle $(C).$
Exercice 11
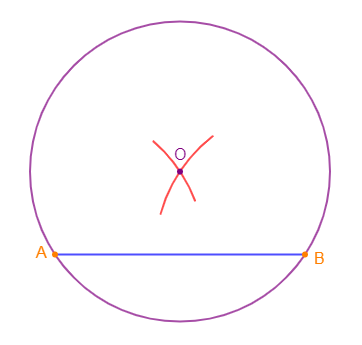
1) Traçons un segment $[AB]$ de longueur $5\;cm.$
2) Construisons un cercle de rayon $3\;cm$ passant par les points $A\ $ et $\ B.$
3) Expliquons notre méthode.
On place d'abord le centre $O$ de ce cercle.
On sait que le centre $O$ de ce cercle doit être à égale distance des points $A\ $ et $\ B$ tels que : $OA=OB=3\;cm$
Donc, avec le compas on fait un écartement de $3\;cm$ puis, on se place sur $A$ et on trace un arc de cercle.
Ensuite, avec le même écartement, on se place sur $B$ et on trace un autre arc de cercle du même côté que le premier arc.
Les deux arcs de cercle se coupent au point $O.$
On marque le point $O$ et avec le même écartement du compas, on se place sur $O$ et on trace le cercle.
On constate alors que ce cercle passe bien par les points $A\ $ et $\ B.$
Exercice 12
On donne la figure ci-dessous :
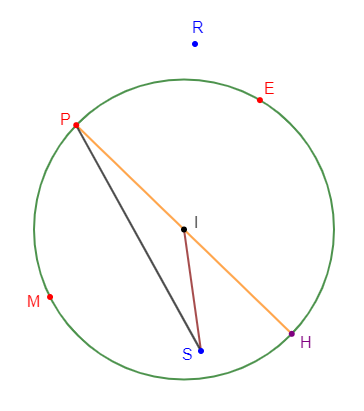
1) $R\ $ et $\ S$ sont deux points n'appartenant pas au cercle.
$\centerdot\ R$ est extérieur au cercle
$\centerdot\ S$ est intérieur au cercle
2) $P\ $ et $\ E$ sont deux points du cercle.
3) Le point $S$ n'appartient pas au cercle.
Sur la figure, on constate que la distance du centre $I$ au point $S$ est plus petite que le rayon du cercle.
Donc, le point $S$ n'appartient pas au cercle.
4) Pour que $[PH]$ soit un diamètre on doit placer $H$ sur le cercle de sorte que les points $P\;;\ I\ $ et $\ H$ soient alignés.
5) Le point $I$ n'est pas un point du cercle.
Justifions notre réponse.
On sait que les points du cercle sont les points situés à une même distance par rapport à un point appelé centre.
Or, on constate que $I$ est à égale distance de tous les points situés sur le cercle.
Donc, $I$ n'est pas un point du cercle. C'est plutôt le centre de ce cercle.
6) Justifions que $[SP]$ n'est pas une corde.
On sait que : une corde est un segment dont les extrémités sont sur le cercle.
Or, on constate que $[SP]$ est un segment dont l'une des extrémités ; le point $S$, n'appartient pas au cercle.
Par conséquent, $[SP]$ n'est pas une corde.
Exercice 13
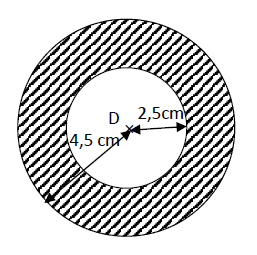
La figure ci-dessous est une couronne délimitée par deux cercles concentriques.
Calculons l'aire de la partie hachurée.

En observant la figure, on remarque que l'aire de la partie hachurée en faisant la différence entre l'aire délimitée par le grand cercle et l'aire délimitée par le petit cercle.
Soit $\mathcal{A}_{1}$ l'aire délimitée par le grand cercle de centre $D$ et de rayon $4.5\;cm\ $ et $\ \mathcal{A}_{1}$ l'aire délimitée par le petit cercle de centre $D$ et de rayon $2.5\;cm$
Alors, on a :
$$\text{Aire de la partie hachurée}=\mathcal{A}_{1}-\mathcal{A}_{2}$$
$-\ $ Calculons l'aire $\mathcal{A}_{1}$
L'aire $\mathcal{A}_{1}$ délimitée par le grand cercle de rayon $r$ est donnée par :
$$\mathcal{A}_{1}=r\times r\times\pi$$
En remplaçant $r$ par $4.5$ et en choisissant $\pi=3.14$, on obtient :
$\begin{array}{rcl}\mathcal{A}_{1}&=&r\times r\times\pi\\\\&=&4.5\times 4.5\times 3.14\\\\&=&63.585\end{array}$
D'où, $\boxed{\mathcal{A}_{1}=63.585\;cm^{2}}$
$-\ $ Calculons l'aire $\mathcal{A}_{2}$
L'aire $\mathcal{A}_{2}$ délimitée par le petit cercle de rayon $r$ est donnée par :
$$\mathcal{A}_{2}=r\times r\times\pi$$
En remplaçant $r$ par $2.5$ et en choisissant $\pi=3.14$, on obtient :
$\begin{array}{rcl}\mathcal{A}_{2}&=&r\times r\times\pi\\\\&=&2.5\times 2.5\times 3.14\\\\&=&19.625\end{array}$
Ainsi, $\boxed{\mathcal{A}_{2}=19.625\;cm^{2}}$
$-\ $ Calculons l'aire de la partie hachurée
L'aire de la partie hachurée est donnée par :
$\begin{array}{rcl}\text{Aire de la partie hachurée}&=&\mathcal{A}_{1}-\mathcal{A}_{2}\\\\&=&63.585-19.625\\\\&=&43.96\end{array}$
D'où, $\boxed{\text{Aire de la partie hachurée}=43.96\;cm^{2}}$
Exercice 14
A l'aide d'une poulie de $15\;cm$ de diamètre, Astou doit puiser de l'eau dans un puits de $9.42\;m$ de profondeur.
Déterminons le nombre de tours que doit faire la poulie pour sortir le seau du puits.
La poulie a une forme circulaire de diamètre $d=15\;cm.$
Donc, un tour est égal au périmètre de ce cercle.
On a alors :
$\begin{array}{rcl}\text{un tour}&=&d\times\pi\\\\&=&15\times 3.14\\\\&=&47.1\end{array}$
Ainsi, chaque tour de la poulie correspond à $47.1\;cm$
La profondeur du puits est égale à $9.42\;m$
Donc, en convertissant en $cm$, on obtient : $9.42\;m=942\;cm.$
Alors, le nombre de tours que doit faire la poulie pour sortir le seau du puits est donné par :
$\begin{array}{rcl}\text{Nombre de tour}&=&\dfrac{\text{Profondeur du puits}}{\text{Périmètre de la poulie}}\\\\&=&\dfrac{942}{47.1}\\\\&=&20\end{array}$
Par conséquent, la poulie doit faire $20$ tours pour sortir le seau du puits.
Exercice 15
Un berger a un enclos circulaire de $12\;m$ de diamètre qu'il veut entourer d'un grillage qui coûte $450\;F$ le mètre et doit y laisser une porte de $3.5\;m.$
Calculons le prix du grillage.
Calculons d'abord la longueur du grillage.
On a :
$$\text{Longueur du grillage}=\text{Périmètre enclos}-\text{Longueur de la porte}$$
Comme l'enclos est circulaire de diamètre $d=12\;m$ alors, son périmètre est donné par :
$\begin{array}{rcl}\text{Périmètre enclos}&=&d\times\pi\\\\&=&12\times 3.14\\\\&=&37.68\end{array}$
Donc, $\boxed{\text{Périmètre enclos}=37.68\;m}$
Ainsi,
$\begin{array}{rcl}\text{Longueur du grillage}&=&\text{Périmètre enclos}-\text{Dimension porte}\\\\&=&37.68-3.5\\\\&=&34.18\end{array}$
D'où, $\boxed{\text{Longueur du grillage}=34.18\;m}$
Calculons ensuite le prix du grillage
Comme le grillage coûte coûte $450\;F$ le mètre alors, le prix total est donné par :
$\begin{array}{rcl}\text{Prix du grillage}&=&450\times\text{Longueur du grillage}\\\\&=&450\times 34.18\\\\&=&15\,381\end{array}$
Ainsi, le prix du grillage est égal à $15\,381\;F$
Auteur:
Diny Faye

Commentaires
Mbacké (non vérifié)
jeu, 03/04/2021 - 23:55
Permalien
Demande un autorisation de voir les Cours et les Exercices.
Anonyme (non vérifié)
mar, 01/18/2022 - 14:36
Permalien
Solution exercices 5
Mame Thierno fall (non vérifié)
dim, 03/06/2022 - 11:46
Permalien
C’est bon pour toutes les
Ajouter un commentaire