Série d'exercices : Gravitation universelle - Ts
Classe:
Terminale
Exercice 1
Un satellite artificiel de la Terre, de masse $m$, se déplace vitesse constante sur une orbite circulaire dans un référentiel galiléen lié au centre de la Terre à l'altitude $h=3.6\cdot10^{7}m$ compté à partir de la surface de la Terre.
La trajectoire est située dans le plan équatorial et le satellite tourne dans le sens de rotation de la Terre.
Le rayon de la Terre est $R=6.4\cdot10^{6}m$
1. Calculer la valeur de l'intensité $g$ du champ de pesanteur à l'altitude $h$, sachant qu'à la surface de la Terre $g_{0}=9.8\,m\cdot s^{-2}.$
On rappelle la loi de la gravitation universelle $F=k\dfrac{Mm}{r^{2}}$0 où $M$ est la masse de la Terre et $r$ la distance du satellite au centre de la Terre.
2. Faire le bilan des forces appliquées au satellite supposé ponctuel et en déduire sa vitesse
3. Déterminer la période du mouvement dans le repère galiléen considéré ici.
Exercice 2
La Terre est assimilée à une sphère de rayon $T_{R}$ et de masse $M_{T}.$
Elle possède une répartition de masse à symétrie sphérique.
1. On suppose galiléen, le repère géocentrique dont l'origine coincide avec le centre de la Terre et dont les axes ont une direction fixe par rapport aux étoiles
Deux corps sphériques de masse $m_{1}$ et $m_{2}$, dont les centres sont distants de $r$ exercent l'un sur l'autre des forces d'attraction ayant pour intensité : $$F=G\dfrac{m_{1}m_{2}}{r^{2}}$$
$G$ est la constante de gravitation univerelle
1.1
1.1.1 Écrire l'expression de l'intensité $F_{0}$ de la force que la Terre exerce sur un corps ponctuel de masse $m=1Kg$ placé à surface
1.1.2 a) Déduire de la question 1.1.1, l'expression de la masse $M_{T}$ de la Terre en fonction de $g_{0}$, $R_{T}$ et $G$
b) Calculer $M_{T}$
On donne :
$G=6.67\cdot10^{-11}S.I$,
$g_{0}=9.8\,m\cdot s^{-2}$,
$R_{T}=6370Km$
1.2 Montrer qu'a l'altitude $h$ au-dessus de la Terre, l'intensité du champ de gravitation est donnée par la relation : $$g=g_{0}\dfrac{R_{T}^{2}}{\left(R_{T}+h\right)^{2}}$$
$g_{0}$ est l'intensité du champ de gravitation terrestre au niveau du sol
2. Un satellite assimilé à un point matériel décrit une orbite circulaire dont son centre est confondu avec celui de la Terre.
Il est à l'altitude $h.$
2.1 Montrer que le mouvement du satellite est uniforme.
2.2 Établir en fonction $g_{0}$, $R_{T}$ et $h.$
2.2.1 la vitesse $v$ du satellite ;
2.2.2 La période $T$ du satellite ;
2.3 Calculer $v$ et $T$
2.4 On pose $r=R_{T}+h$
2.4.1 Montrer que le rapport $\dfrac{T^{2}}{r^{3}}=cte$ est égal à un constante.
C'est la $3^{e}$ de Kepler
2.4.2 Exprimer le rapport $\dfrac{T^{2}}{r^{3}}=cte$ en fonction de $M_{T}$ et $G$
2.4.3 Calculer la masse $M_{T}$ de la Terre.
Cette valeur est-elle compatible avec celle de la question 1.1.2
On donne $h=300Km.$
Exercice 3
La terre est assimilée à une sphère homogène de centre $O$ de masse $M$ et de rayon $R.$
Le champ de gravitation crée par la Terre en tout point $A$ de l'espace situé à une distance $r$ du point $O$ est :
$$\overrightarrow{\mathfrak{G}}=-\dfrac{GM}{r^{2}}\overrightarrow{u}\quad\text{et}\quad\overrightarrow{u}=\dfrac{\overrightarrow{OA}}{\|\overrightarrow{OA}\|}$$
$G$ : Constante universelle de gravitation
1. Un satellite $(S)$ de masse $m$ décrit un mouvement uniforme sur une orbite circulaire de $r$ autour de la Terre.
Le mouvement est rapporté par rapport au repère géocentrique et on suppose que $(S)$ soumis à la seule action du champ de gravitation terrestre
1.1 Exprimer la vitesse $V$ de $(S)$ en fonction de l'intensité $G_{0}$ du champ de gravitation du sol, de $R$ et $r$
1.2 En déduire l'expression de la période $T$ du mouvement.
Calculer $T$
On donne $R=6400Km$ ;
$G_{0}=9.8\,m\cdot s^{-2}$ ;
$r=8000Km$
2.
2.1 A partir du travail élémentaire $\mathrm{d}w=-f\mathrm{d}r$ de la force de gravitation exercée par la Terre sur le satellite ; montrer que le travail de cette force lors du déplacement du sol jusqu'à l'orbite de rayon $r$ est donné par : $$W=mG_{0}R^{2}\left(\dfrac{1}{r}-\dfrac{1}{R}\right)$$
2.2 En déduire l'expression de l'énergie potentielle du système Terre-satellite en fonction de $G_{0}$, $m$, $r$ et $R.$
On choisira le niveau du sol comme étant de référence pour l'énergie potentielle
2.3 Exprimer l'énergie cinétique de $(S)$ en fonction de $G_{0}$, $m$, $r$ et $R$
En déduire l'expression de l'énergie mécanique $E$
3. Il se produit une très faible variation $\mathrm{d}r$ du rayon $r$, telle que la trajectoire puisse toujours être considéré comme circulaire
3.1 Exprimer la variation $\mathrm{d}v$ de la vitesse qui en résulte et montrer que $\mathrm{d}v=-\dfrac{\pi}{T}\mathrm{d}r$
3.2 La variation de $\mathrm{d}r$ est en réalité due au travail $\mathrm{d}w_{f}$ des forces de frottements exercées par les couches raréfiées de l'atmosphère pendant le déplacement.
Du signe de $\mathrm{d}w_{f}$, déduire l'effet de ces forces sur l'altitude et la vitesse de $(S).$
Exercice 4
On assimile le Soleil à une sphère de rayon $R_{S}$ et de masse $M_{S}$ présentant une répartition de masse à symétrie sphérique.
On suppose que la trajectoire de la Terre autour du Soleil est un cercle de rayon $r.$
1. Donner l'expression littérale du champ de gravitation $G_{0S}$ à la surface du Soleil.
Calculer sa valeur numérique.
2. Donner l'expression littérale du champ de gravitation $G_{S}$ en un point de l'orbite terrestre autour du Soleil.
Calculer sa valeur numérique.
3. Comparer la valeur du champ de gravitation $G_{S}$ précédente à celle $G_{0}T$ du champ de gravitation terrestre au niveau du sol.
Conclure.
Données :
$R_{S}=7.0\cdot10^{5}km$
$M_{S}=2.0\cdot10^{30}kg$
$r=1.5\cdot10^{8}km$
Constante de gravitation universelle : $G=6.67\cdot10^{-11}S.I.$
Champ de gravitation au niveau du sol : $G_{0}T=9.8\,N\cdot kg^{-1}$
Soit $M_{L}$ et $M_{T}$ les masses respectives de la Lune et de la Terre, ces astres étant supposés sphériques.
Soit $R_{L}$ et $R_{T}$ leurs rayons.
On a les relations $M_{T}=81\cdot M_{L}$ et $R_{T}=\dfrac{11}{3}R_{L}.$
4. Calculer la valeur du champ de gravitation lunaire $G_{0}L$ au niveau de son sol.
5. Il existe sur la ligne joignant les deux astres Terre et Lune un point où les champs de gravitation lunaire et terrestre se compensent.
a) Situer ce point $M$ remarquable en calculant sa distance $d$ au centre de la Terre.
b) Indiquer, sur le segment Terre-Lune, le domaine où l'action gravitationnelle d'un des deux astres est prépondérante.
Données :
Distance Terre-Lune : $D=380\ 000\,km.$
Exercice 5
Données :
Masse de la Terre $M_{T}=5.97\times 10^{24}kg$
Rayon de la Terre $R_{T}=6.38\times 10^{6}m$
Masse du Soleil $M_{S}=333\times 10^{3}\times M_{T}$
Constante universelle de gravitation $G=6.67\times 10^{-11}S.I.$
Valeur du champ de pesanteur au niveau du sol $g=9.81\,m/s^{2}$
1 Lancement d'un satellite
On étudie le lancement d'un satellite artificiel à partir d'un point $O$ de la surface terrestre.
1.a) Établir l'expression de la vitesse du point $O$ de la surface terrestre.
Dans le référentiel géocentrique $R_{g}$ (assimilé ici à un référentiel galiléen) en fonction de la vitesse angulaire de rotation de la Terre autour de l'axe de ses pôles $($cette vitesse angulaire est notée $\Omega)$, du rayon terrestre $R_{T}$ et de la latitude $\lambda$ du lieu du lancement.
1.b) En déduire les conditions les plus favorables pour le lancement du satellite.
Parmi les trois champs de tirs suivants, lequel choisir de préférence ?
Baïkonour au Kazakhstan $\lambda=46^{\circ}$ ;
Cap Canaveral aux USA $\lambda=28.5^{\circ}$ ;
Kourou en Guyane française $\lambda=5.23^{\circ}.$
1.c) Établir l'expression de l'énergie potentielle de gravitation d'un satellite en fonction de son altitude $z$ par rapport au sol.
On prend pour référence une énergie potentielle nulle à l'infini.
En déduire l'expression de l'énergie mécanique du satellite sur sa base de lancement dans le référentiel géocentrique.
1.d) On appelle ici vitesse de libération $v_{1}$, la vitesse verticale minimale qu'il faut communiquer initialement au satellite par rapport au sol, pour qu'il puisse se libérer de l'attraction terrestre.
Donner l'expression de $v_{1}.$
Calculer sa valeur numérique dans le cas où le satellite est lancé de la base de Kourou (on tient donc compte de la rotation de la terre).
2. Satellite artificiel en orbite
On considère un satellite artificiel de masse $m$ en mouvement circulaire autour de la Terre.
2.a) Montrer que le mouvement du satellite est uniforme.
Établir l'expression de la vitesse du satellite en fonction de son altitude ainsi que la troisième loi de Kepler liant la période de rotation $T$ du satellite au rayon $r$ de sa trajectoire.
2.b) Calculer le rayon de l'orbite d'un satellite géostationnaire .
2.c) Soit un satellite d'énergie mécanique initiale $Em_{0}.$
Son orbite est relativement basse et il subit donc les frottements des couches hautes de l'atmosphère.
Il s'ensuit que l'énergie mécanique du satellite varie selon la loi :
$Em=Em_{0}(1+bt)$, $b$ étant un coefficient constant positif.
En supposant que la trajectoire reste approximativement circulaire.
Établir l'expression du rayon $r$ et de la vitesse $v$ du satellite en fonction du temps.
Comparer les évolutions de $r$ et de $v$ ainsi que celles des énergies potentielle et cinétique.
Que devient l'énergie perdue ?
Exercice 6
Pour mettre un satellite en orbite, une fusée $a$, au décollage, une poussée de $7.5\cdot10^{5}N.$
La masse totale de la fusée est de $40$ tonnes.
1. Quelle est l'accélération de la fusée ?
2. Le satellite est placé sur une orbite circulaire de rayon $r.$
Exprimer la vitesse $v$ et la période $T$ du mouvement du satellite en fonction de $K$, constante universelle de gravitation, $r$ et $M$, la masse de la terre.
En déduire que $\dfrac{T^{2}}{R^{3}}=\text{constante}.$
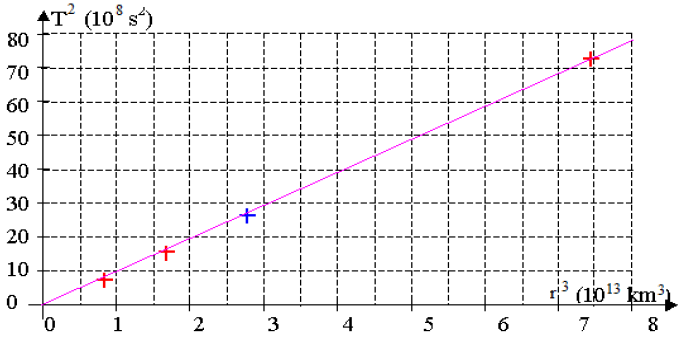
3. La courbe reproduite en annexe donne la représentation graphique de $T^{2}$ en fonction de $r^{3}.$
Elle est obtenue à partir de données numériques sur la période $T$ et le rayon $r$ de quelques satellites qui tournent autour de la Terre.
Déduire de la courbe la valeur de la masse $M$ de la Terre.
$K=6.67\cdot10^{-11}U.S.I.$
4. Le satellite est placé sur une orbite de rayon $r$, contenu dans le plan équatorial.
a) Exprimer les énergies potentielles $E_{P}$, $E_{C}$ et totale $E_{T}$ du satellite en fonction de la masse $M$ de la Terre, de la masse $m$ du satellite et de $r.$
$« E_{P}$ est nulle lorsque le satellite est infiniment éloigné de la Terre $».$
b) Avant d'être placé sur son orbite de rayon $r$, le satellite, était posé sur le sol, en un point $P$ de latitude $\gamma.$
Sa vitesse était, la vitesse $V_{e}$ due à la rotation de la Terre, supposée sphérique de rayon $R.$
Donner l'expression de $V_{e}$ en fonction de $ω_{T}$, vitesse angulaire de rotation de la Terre, $R$ et $\gamma.$
Déterminer les expressions des énergies potentielles $E_{P1}$, cinétique $E_{C1}$ et totale $E_{T1}$ du satellite au point $P.$
5. a) Pour placer le satellite sur son orbite, il a fallu lui fournir l'énergie $\Delta E=E_{T}-E_{T1}.$
Montrer que $\Delta E$ varie avec $\gamma.$
b) On considérera que le satellite tourne dans le même sens que la Terre.
Où doit-on choisir les bases de lancement pour l'énergie $\Delta E$ soit minimale ?
6. La première vitesse cosmique $V_{1}$ est la vitesse de satellisation circulaire à basse altitude autour de la Terre d'un engin spatial.
Calculer $V_{1}$ à l'altitude $h=100\,km.$
On donne $R=6400\,km$ et la masse $M$ de la Terre.
Exercice 7
Un satellite supposé ponctuel, de masse $m_{S}$, décrit une orbite circulaire d'altitude $h$ autour de la Terre assimilée à une sphère de rayon $R_{T}.$
On fera l'étude dans un référentiel géocentrique considéré comme galiléen.
1. Établir l'expression de l'intensité $g$ du vecteur champ de pesanteur à l'altitude $h$ en fonction de sa valeur $g_{0}$, au niveau du sol, de $R_{T}$ et de $h.$
2. Déterminer l'expression de la vitesse $v_{S}$ du satellite, celle de sa période et de son énergie cinétique.
Application numérique :
$m_{S}=1020\,kg$ ;
$g_{0}=9.81\,m/s^{2}$ ;
$R_{T}=6400\,Km$ ;
$h=400\,km.$
3. L'énergie potentielle du satellite dans le champ de pesanteur à l'altitude $h$ est donnée par la relation :
$$E_{P}=-\dfrac{Km_{S}M_{T}}{R_{T}+h}$$ avec $K$, constante de gravitation et $M_{T}$ masse de la Terre et en convenant que $E_{P}=0$ pour $h_{P\infty}.$
Justifier le signe négatif et exprimer $E_{P}$ en fonction de $m_{S}$, $g_{0}$, $R_{T}$ et $h.$
Déterminer l'expression de l'énergie mécanique $E$ du satellite puis comparer $E_{P}$ à $E_{C}$ et $E$ à $E_{C}.$
4. On fournit au satellite un supplément d'énergie $\Delta E=+5\cdot10^{8}J.$
Il prend alors une nouvelle orbite circulaire.
Déterminer :
a) Sa nouvelle énergie cinétique et sa vitesse
b) Sa nouvelle énergie potentielle et son altitude.
Exercice 8
Le $15$ octobre $1997$, le véhicule spatial Cassini emportait à son bord la sonde HUYGENS destinée à l'exploration des anneaux de Saturne.
Titan, le plus gros satellite de Saturne, a été découvrent en $1665$
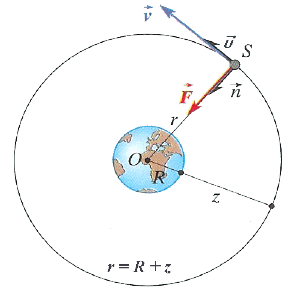
On étudie le mouvement supposé circulaire de Titan dans le référentiel centré sur Saturne et dont les trois axes sont dirigés vers trois étoiles lointaines supposées fixes
1. Reproduire le schéma ci-dessus et représenter qualitativement la force gravitationnelle qui agit sur Titan
2. Donner l'expression vectorielle de cette force
3. Établir du vecteur accélération du centre d'inertie de Titan sur son orbite et le représenter qualitativement sur le schéma précédent
4. Montrer que le mouvement de Titan sur son orbite est uniforme
5. Établir en fonction de $G$ $M_{S}$ et $r_{T}$ :
5.1 l'expression de la vitesse $V_{T}$ du centre d'inertie de Titan
5.2 l'expression de la période de révolution $T_{T}$ de Titan autour de Saturne
6. Montrer qu'au cours de sa révolution autour de Saturne :
$\dfrac{T_{T}^{2}}{r_{T}^{3}}=K=\text{constante}$ $(3^{e}$ loi de Kepler$)$
7. En fait Saturne possède un cortège de satellites dont au moins $60$ ont été identifiés à ce jour.
Parmi eux, figurent Rhéa et Dioné découverts par Jean Dominique Cassini respectivement en $1672$ et $1684$
7.1 Montrer que ces deux satellites vérifient la $3^{e}$ loi de Kepler
7.2 En déduire la masse $M_{S}$ de Saturne
On donne :
$-\ $ Constante de gravitation universelle $G$ : $G=6.67\cdot10^{-11}S.I$
$-\ $ Rayon de l'orbite de Rhéa $r_{R}=527070\,Km$
$-\ $ Période de révolution de Rhéa autour de Saturne $T_{R}=4.518\,jours$ soit $390355\,s$
$-\ $ Rayon de l'orbite de Dioné $r_{D}=377400\,Km$
$-\ $ Période de révolution de Dioné autour de Saturne $T_{D}=2.737\;jours$ soit $236477\,s$

Commentaires
Papa DOUMBOUYA (non vérifié)
mer, 01/29/2020 - 17:11
Permalien
Il y'a pas de solutions pour les exercices gravitationnel
Anonyme (non vérifié)
jeu, 02/04/2021 - 22:41
Permalien
Merci beaucoup pour tt
Daouda Ndiaye (non vérifié)
mar, 03/09/2021 - 08:05
Permalien
Bac
DENEKA (non vérifié)
lun, 11/27/2023 - 22:48
Permalien
Correction de l’exercice 2
DENEKA (non vérifié)
lun, 11/27/2023 - 22:48
Permalien
Correction de l’exercice 2
Ajouter un commentaire