Vous êtes ici

Solution des exercices : Le poids - La masse - Relation entre poids et masse - 2nd S

Classe:

Seconde

Exercice 1

Un solide en aluminium de masse $m=30\;g$ et de volume $V=12\;cm^{3}.$

1) Calculons sa masse volumique $\rho$ en $g.cm^{-3}$ puis en $kg.m^{-3}.$

Soit : $\rho=\dfrac{m}{V}$

A.N : $\rho=\dfrac{30}{12}=2.5$

D'où, $\boxed{\rho=2.5\;g.cm^{-3}}$

Exprimons le résultat en $kg.m^{-3}.$

On a :

$\begin{array}{rcl}\rho&=&2.5\;g.cm^{-3}\\ \\&=&2.5\times 10^{-3}\;kg\times 10^{6}\;m^{-3}\\ \\&=&2.5\cdot 10^{3}\;kg.m^{-3}\end{array}$

Ainsi, $\boxed{\rho=2.5\cdot 10^{3}\;kg.m^{-3}}$

2) Calculons sa densité $d$ par rapport à l'eau (on donne : $\rho_{\text{eau}}=1\;g.cm^{-3}$)

Soit : $d=\dfrac{\rho}{\rho_{\text{eau}}}$

A.N : $d=\dfrac{2.5}{1}=2.5$

Donc, $\boxed{d=2.5}$

3) Sachant que la masse volumique de l'aluminium est $\rho_{Al}=2.7\;g.cm^{-3}$ écrivons "Vrai" ou "Faux" devant chacune des affirmations suivantes :

a) Si le solide est plein alors il est en aluminium pur.$\quad\text{Faux}$

b) Si le solide est plein alors il est un alliage d'aluminium et d'un autre métal de masse volumique inférieure à $2.7\;g.cm^{-3}.\quad\text{Faux}$

c) Si le solide est en aluminium pur alors il est plein.$\quad\text{Faux}$

4) Sachant que le solide est en aluminium pur.

a) Montrons qu'il est creux.

Déterminons la masse $m'$ de l'aluminium à partir de $\rho_{Al}=2.7\;g.cm^{-3}$

On a : $m'=\rho_{Al}.V$

Soit : $m'=2.7\times 12=32.4\;g$

Par suite, $m'>m.$ Ce qui montre que le solide est creux.

b) Déterminons le volume $V_{c}$ de la cavité située à l'intérieure du solide

On a : $V_{c}=\dfrac{m'-m}{\rho_{Al}}$

A.N : $V_{c}=\dfrac{32.4-30}{2.7}=8.9$

D'où, $\boxed{V_{c}=8.9\;mL}$

Exercice 2

Un corps solide $(S)$ de masse $m=75\;g$ a la forme d'un cube d'arête $a=5\;cm.$

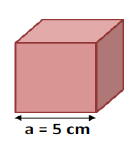
1) Calculons le volume du solide $(S).$

Le solide étant de forme cubique d'arête $a$ alors, son volume $V$ est donné par :

$$V=a^{3}$$

A.N : $V=5^{3}=125$

Donc, $\boxed{V=125\;cm^{3}}$

2) Calculons la masse volumique du solide $(S)$ en $g.cm^{-3}$ et en $kg.m^{-3}.$

Soit : Soit : $\rho_{(S)}=\dfrac{m}{V}$

A.N : $\rho_{(S)}=\dfrac{75}{125}=0.60$

D'où, $\boxed{\rho_{(S)}=0.60\;g.cm^{-3}}$

En exprimant le résultat en $kg.m^{-3}$, on obtient :

$\boxed{\rho_{(S)}=600\;kg.m^{-3}}$

3) Le solide $(S)$ est du bois, d'après le tableau ci-dessous car sa masse volumique correspond à celle du bois.

$$\begin{array}{|l|c|c|c|c|}\hline\text{Corps}&\text{Aluminium}&\text{Cuivre}&\text{Liège}&\text{Bois}\\\hline\rho\,(kg.m^{-3})&2700&8900&240&600\\\hline\end{array}$$

4) Calculons la densité du solide $(S)$ par rapport a l'eau.

Soit : $d=\dfrac{\rho_{(S)}}{\rho_{\text{eau}}}$

A.N : $d=\dfrac{600}{1000}=0.60$

Ainsi, $\boxed{d=0.60}$

5) On introduit le solide $(S)$ dans un récipient contenant de l'eau.

Le solide $(S)$ flotte à la surface de l'eau car la densité est inférieure à l'unité $(d<1)$

Exercice 3

I. Un commerçant désire acheter de l'huile pure, il pratique la démarche expérimentale suivante en utilisant un échantillon d'huile comme le montre la figure suivante :

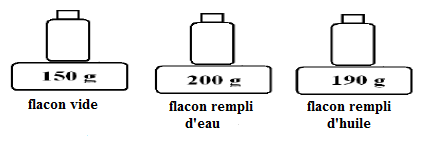
1) A partir des pesées précédentes, calculons :

a) La masse $m$ d'eau

On a : $m=200-150=50$

Donc, $\boxed{m=50\;g}$

b) La masse $m'$ d'huile

Soit : $m'=190-150=40$

Donc, $\boxed{m'=40\;g}$

c) On donne $\rho_{eau}=1\;g.cm^{-3}$

Déduisons le volume d'eau $V$ contenu dans le flacon en $cm^{3}$ puis en $l.$

On a : $V=\dfrac{m}{\rho_{\text{eau}}}$

A.N : $V=\dfrac{50}{1}=50$

D'où, $\boxed{V=50\;cm^{3}=0.05\;L}$

2) a) Déterminons la densité $d'$ de l'huile par rapport à l'eau.

Soit : $d'=\dfrac{m'}{m}$

Donc, $d'=\dfrac{40}{50}=0.80$

D'où, $\boxed{d'=0.80}$

b) On a : $\rho\neq\rho_{\text{huile}}.$

Par conséquent, l'huile que désire acheter le commerçant n'est pas de l'huile pure.

II. On dispose d'un bêcher de capacité $100\;ml$ et d'un corps $C$ de forme cubique de $4\;cm$ de côté

1) Calculons le volume $V$ du corps $C.$

Soit : $V=a^{3}=4^{3}=64$

Donc, $\boxed{V=64\;cm^{3}}$

2) Vérifions si on peut mesurer le volume du corps $C$ en l'introduisant dans un bêcher contenant $50\;mL$ d'eau.

Déterminons le volume du bêcher contenant l'eau et corps $C$

Soit : $V'=64+50=114\;mL$

On a : $V_{\text{bêcher}}=100\;mL<V'$ donc, on ne peut pas mesurer le volume du corps $C$ en l'introduisant dans un bêcher, car une quantité d'eau se déverse

3) Calculons le volume d'eau déversée $V_{D}$ lorsqu'on met le corps $C$ dans le bêcher

On a :

$\begin{array}{rcl} V_{D}&=&V'-V_{\text{bêcher}}\\ \\&=&114-100\\\\&=&14\end{array}$

Donc, $\boxed{V_{D}=14\;mL}$

Exercice 4

1.a. Détermination de la masse $m_{1}$ du liquide $L_{1}$

$\begin{array}{rcl} m_{1}&=&80-47\\\Rightarrow\boxed{m_{1}=33\;g }\end{array}$

b. Calcul de la masse volumique $\rho_{1}$ du liquide $L_{1}$ en $g\cdot cm^{-3}$ puis en $kg\cdot m^{-3}$

$\begin{array}{rcl} \rho_{1}&=&\dfrac{m_{1}}{V_{1}}\\&=&\dfrac{33}{40}\\\Rightarrow\rho_{1}&=&0.825\,gcm^{-3}\\\Rightarrow\boxed{\rho_{1}=825\,kgm^{-3}} \end{array}$

c. Déduisons la densité $d_{1}$ du liquide $L_{1}$ par rapport à l'eau.

$\begin{array}{rcl} d_{1}&=&\dfrac{\rho_{1}}{\rho_{\text{eau}}}\\&=&\dfrac{0.825}{1}\\\Rightarrow\boxed{d_{1}=0.825} \end{array}$

2.a. Détermination de la masse $m_{2}$ du liquide $L_{2}$

$\begin{array}{rcl} m_{2}93-47\\\Rightarrow\boxed{m_{2}=36\;g} \end{array}$

b. Calcul de la masse volumique $\rho_{2}$ du liquide $L_{2}$ en $g\cdot cm^{-3}$ puis en $kg\cdot m^{-3}$

$\begin{array}{rcl} \rho_{2}&=&\dfrac{m_{2}}{V_{2}}\\&=&\dfrac{36}{50}\\\Rightarrow\rho_{2}&=&0.72\,gcm^{-3}\\\Rightarrow\boxed{\rho_{2}=720\,kgm^{-3}} \end{array}$

c. Déduisons la densité $d_{2}$ du liquide $L_{2}$ par rapport à l'eau.

$\begin{array}{rcl} d_{2}&=&\dfrac{\rho_{2}}{\rho_{\text{eau}}}\\&=&\dfrac{0.72}{1}\\\Rightarrow\boxed{d_{2}=0.72} \end{array}$

3. Le liquides est le plus dense $d_{2}\succ\,d_{1}.$

Le liquide $L_{1}$ est le plus dense

4.a. La nature du mélange obtenu.

Le mélange obtenu est un mélange hétérogène

b. Calcul de la masse volumique du mélange

$\begin{array}{rcl} \rho&=&\dfrac{m_{1}+m_{2}}{V_{1}+V_{2}}\\&=&\dfrac{33+36}{40+50}\\\Rightarrow\boxed{\rho=0.77\,gcm^{-3}} \end{array}$

$\begin{array}{rcl}\text{ou } \rho&=&\dfrac{\rho_{1}V_{1}+\rho_{2}V_{2}}{V_{1}+V_{2}}\\&=&\dfrac{0.825\times 40+0.72\times 50}{40+50}\\\Rightarrow\boxed{\rho=0.77\,gcm^{-3}} \end{array}$

$\begin{array}{rcl} \text{ou }\rho&=&\dfrac{d_{1}\rho_{\text{eau}}V_{1}+d_{2}\rho_{\text{eau}}V_{2}}{V_{1}+V_{2}}\\&=&\dfrac{d_{1}V_{1}+d_{2}V_{2}}{V_{1}+V_{2}}\rho_{\text{eau}}\\&=&\dfrac{0.825\times40+0.72\times50}{40+50}\times1\\\Rightarrow\boxed{\rho=0.77\,gcm^{-3}} \end{array}$

Exercice 5

1.Complétons le tableau de mesures suivantes:

$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{Masse m (en g)}&0&100&200&400&700&1000\\ \hline \text{Poids P (en N)}&0&1&2&4&7&10\\ \hline \end{array}$

2. Construisons la courbe donnant le poids $P$ en fonction de la masse $m.$

Échelle : $1\,cm$ pour $100\,g$ et $1\;cm$ pour $1\,N$

3. Allure de la courbe obtenue

La courbe obtenue est une droite linéaire

4. Déduisons pour le poids et la masse la relation qui les lient

Le poids et la masse sont des grandeurs proportionnelles

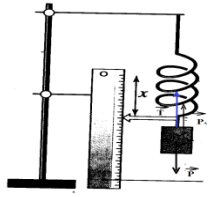
Exercice 6 : Réalisation d'un dynamique

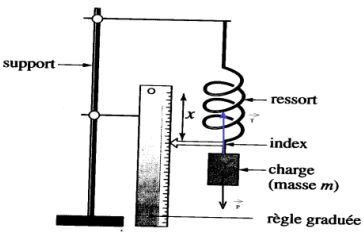
1.a Les force s'exerçant sur le solide sont :

$-\ $Le poids $\overrightarrow{P}$

$-\ $La tension du ressort $\overrightarrow{T}$

b. La somme des forces sur le solide est nulle car le solide est en équilibre :

$\overrightarrow{P}+\overrightarrow{T}=\overrightarrow{0}$

c. Déduisons une relation entre m (valeur de la masse suspendue) et $T$ (norme de la force exercée par le ressort sur la masse).

$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{T}&=&\overrightarrow{0}\\\Rightarrow\;mg-T&=&0\\\Rightarrow\boxed{T=mg }\end{array}$

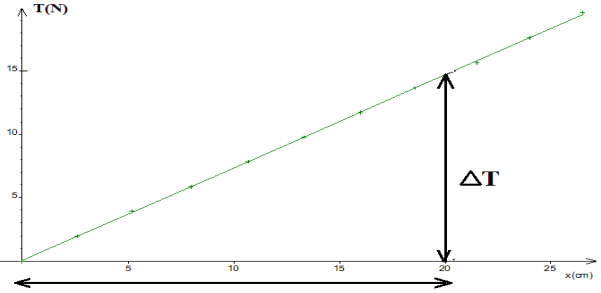
2. Construction du graphique donnant $T$ en fonction de $x$

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|} \hline m(kg)&0&0.20&0.40&0.60&0.80&1.00&1.20&1.40&1.60&1.80&2.00\\ \hline x(cm)&0&2.6&5.2&8.0&10.7&13.3&16.0&18.6&21.5&24.0&26.5\\ \hline T(N)&0&1.9&3.9&5.9&7.8&9.8&12&13&16&18&19\\ \hline \end{array}$$

Cette longueur représente l'allongement du ressort

3. Déduction de la valeur de la raideur du ressort et son unité.

$\begin{array}{rcl} k&=&\dfrac{\Delta T}{\Delta x}\\&=&\dfrac{14.5-0}{(20-0)\cdot 10^{2}}\\\Rightarrow\boxed{k=72.5\,N\cdot m^{-1}} \end{array}$

4.a Déduisons sa masse en utilisant le graphique.

$\begin{array}{rcl} T&=&mg\\\Rightarrow\;m&=&\dfrac{T}{g}\ ;\\x_{1}&=&16\;cm\\\Rightarrow\;T&=&12\,N\\\Rightarrow\;m&=&\dfrac{12}{10}\\\Rightarrow\boxed{m=1.2\,kg} \end{array}$

b. Schéma des forces appliquées sur me système.

$-\ $Déduisons l'expression littérale du volume de la boite.

$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{T}+\overrightarrow{P}_{A}&=&\overrightarrow{0}\\\Rightarrow\;mg-T-\rho_{\text{eau}}V_{ig}&=&0\\\Rightarrow\boxed{V_{i}=\dfrac{mg-kx_{2}}{\rho_{\text{eau}}g}} \end{array}$

Calcul de sa valeur.

$\begin{array}{rcl}V_{i}&=&\dfrac{mg-kx_{2}}{\rho_{\text{eau}}g}\\&=&\dfrac{1.20\times10-72.5\times10\cdot10^{-2}}{1000\times 10}\\\Rightarrow\;V_{i}&=&4.75\cdot10^{-4}m^{3}\\\Rightarrow\boxed{V_{1}=0.475L} \end{array}$

5. Déterminons graphiquement la valeur de la force nécessaire pour produire l'arrachement.

On trouve graphiquement $F=14.5\,N$

Exercice 7

Pour déterminer la densité du fer, on réalise les deux expériences suivantes :

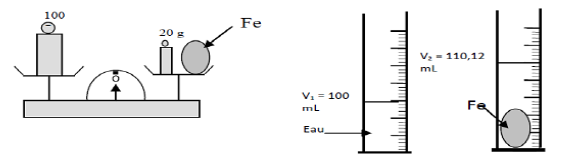
1) Détermination de la masse $m$ du fer.

D'après la première expérience à l'aide de la balance, on a :

$$m+20=100$$

Ce qui entraine : $m=100-20=80$

D'où, $\boxed{m=80\;g}$

2) Détermination du volume $V$ du fer

D'après la deuxième expérience avec les tubes, on peut écrire :

$$V+V_{1}=V_{2}$$

Ce qui donne :

$\begin{array}{rcl} V&=&V_{2}-V_{1}\\\\&=&110.12-100\\\\&=&10.12\end{array}$

Donc, $\boxed{V=10.12\;mL}$

3) Déduction de la masse volumique $\rho_{_{\text{Fer}}}$ du fer dans S.I.

En effet, la la masse volumique $\rho_{Fer}$ du fer dans S.I est donnée par :

$$\rho_{_{\text{Fer}}}=\dfrac{m}{V}$$

A.N : $\rho_{_{\text{Fer}}}=\dfrac{80}{10.12}=7.9$

D'où, $\boxed{\rho_{_{\text{Fer}}}=7.9\;g.cm^{-3}}$

4) Calcul de la densité $d$ du fer. Sachant que $\rho_{_{\text{eau}}}=1\;g.cm^{-3}$

La densité $d$ du fer est donnée par :

$$d=\dfrac{\rho_{_{\text{Fer}}}}{\rho_{_{\text{eau}}}}$$

A.N : $d=\dfrac{7.9}{1}=7.9$

Ainsi, $\boxed{d=7.9}$

5) Expliquons pourquoi si on lance un clou de fer dans l'eau il tombe au fond.

Si on lance un clou de fer dans l'eau il tombe au fond, c'est parce que le fer est plus dense que l'eau.

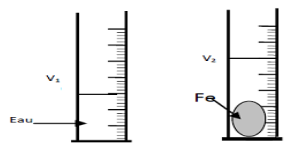
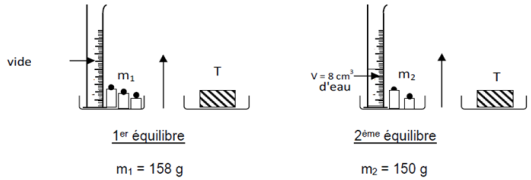
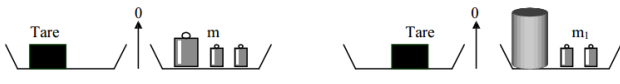
Exercice 8

1. Détermination, en $8\;cm^{3}$, du volume $V$ du solide

$\begin{array}{rcl} V&=&a^{3}\\&=&2^{3}\\\Rightarrow\boxed{V=8\;cm^{3}} \end{array}$

2. Proposons une autre méthode permettant de déterminer ce volume.

On peut utiliser la méthode du volume d'eau déplacé Faisons un schéma.

3.a. Rappel de l'expression de la masse volumique en précisant la signification de

de chaque terme.

$\rho=\dfrac{m_{\text{fer}}}{V}\Rightarrow\;V$ : volume du solide,

$m$ : masse du solide

b. Montrons que la masse volumique du fer est $\rho_{\text{Fer}}=7.9\,g\cdot cm^{-3}$

$\begin{array}{rcl} \rho_{\text{Fer}}&=&\dfrac{m_{\text{Fer}}}{V}\\&=&\dfrac{63.2}{8}\\\Rightarrow\boxed{\rho_{\text{Fer}} =7.9\,g\cdot cm^{-3}} \end{array}$

4.a. Détermination de, en $g$, la masse $m_{\text{eau}}$ du volume $V=8\,cm^{-3}$ d'eau.

$\begin{array}{rcl} m_{\text{eau}}+m_{2}\\&=&m_{1}\\\Rightarrow\;m_{\text{eau_{2}}}&=&m_{1}-m_{2} \\&=&158-150\\\Rightarrow\boxed{m_{\text{eau}}=8\,g} \end{array}$

b. Exprimons la densité $d$ du fer par rapport à l'eau en fonction de $m_{\text{eau}}$

et $m_{\text{eau}}$

$d=\dfrac{m_{\text{Fer}}}{m_{\text{eau}}}$

c. Calculer $d.$

$\begin{array}{rcl} d&=&\dfrac{m_{\text{Fer}}}{m_{\text{eau}}}\\&=&\dfrac{63.2}{8}\\\Rightarrow\boxed{d=7.9} \end{array}$

Exercice 9

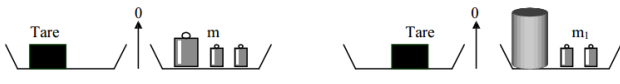
1.a. Calcul du volume de cylindre

$\begin{array}{rcl} V&=&\pi r^{2}h\\&=&\pi\times 2_{2}\times10\\\Rightarrow\boxed{V=125.7\;cm^{3}} \end{array}$

b. Détermination de sa masse

$\begin{array}{rcl} \rho_{Pb}&=&\dfrac{m_{Pb}}{V}\\&=&\dfrac{1.42\cdot10^{3}}{125.7}\\\Rightarrow\rho_{Pb} \\&=&11.3\,g\cdot cm^{-3}\\\Rightarrow\boxed{\rho_{Pb}=1130\,kg\cdot m^{-3}} \end{array}$

b. Détermination de la densité du plomb par rapport à l'eau

$\begin{array}{rcl} d&=&\dfrac{\rho_{Pb}}{\rho_{\text{eau}}}\\&=&\dfrac{11.3}{1}\\\Rightarrow\boxed{d=11.3} \end{array}$

c. La hauteur de l'eau dans l'éprouvette sera la somme de la hauteur du plomb et de la hauteur de l'eau au dessus du cylindre.

3. Détermination du volume de la sphère;

$\begin{array}{rcl} V&=&\dfrac{m}{\rho_{\text{Fer}}}\\&=&\dfrac{m}{d_{\text{Fer}}\rho_{\text{eau}}} \\&=&\dfrac{7.9}{1\times 7900}\\ \Rightarrow\boxed{V=1\,mL} \end{array}$

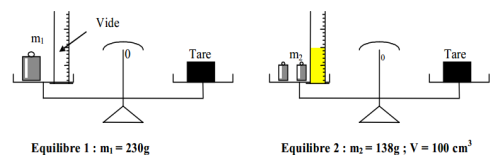
Exercice 10

1. Écrivons les égalités correspondantes pour chaque équilibre

$m_{1}+m_{\text{éprouvett e}}=m_{\text{Tare}}$

$m_{2}+m_{\text{éprouvette }}+m_{\text{huile}}=m_{\text{Tare}}$

2. Déduction de la masse de l'huile

$\begin{array}{rcl} m_{\text{huile}}&=&m_{1}-m_{2}\\&=&230-138\\\Rightarrow\;m_{\text{huile}}&=&92\,g \end{array}$

3. Détermination de la masse volumique de l'huile en $g\cdot cm^{-3}$ et $Kg\cdot m^{-3}$

$\begin{array}{rlc} \rho_{\text{huile}}&=&\dfrac{m_{\text{hule}}}{V}\\&=&\dfrac{92}{100}\\\Rightarrow\rho_{\text{huile}}&=&0.92\,g\cdot cm^{-3} \end{array}$

4. Détermination de la densité de l'huile par rapport à l'eau .

$\begin{array}{rcl} d&=&\dfrac{\rho_{\text{huile}}}{\rho_{\text{eau}}}\\&=&\dfrac{0.92}{1}\\\Rightarrow\;d&=&0.92 \end{array}$

L'eau est plus lourd(ou plus dense) que l'huile

5. a.Détermination de la masse de mercure

$\begin{array}{rcl} m&=&m_{2}-m_{1}\\&=&230-94\\\Rightarrow\;m&=&136\,g \end{array}$

b. Détermination de la masse volumique du mercure en $g\cdot cm^{-3}$ et $Kg\cdot m^{-3}$

$\begin{array}{rcl} \rho_{\text{mercure }}&=&\dfrac{m}{V}\\&=&\dfrac{136}{10}\\\Rightarrow\rho_{\text{mercure }}&=&13.6\,g\cdot cm^{-3 }\boxed{\rho_{\text{mercure}}=13.6\cdot kg\cdot m^{-3} }\end{array}$

c. Déterminer la densité du mercure par rapport à l'eau.

Conclure $\begin{array}{rcl} d&=&\dfrac{\rho_{\text{mercure}}}{\rho_{\text{eau}}}\\&=&\dfrac{13.6}{1}\\\Rightarrow\;d&=&13.6 \end{array}$

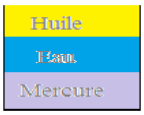
6. Représentons sur un schéma le mélange hétérogène obtenu et expliquons

Le mercure étant le corps le plus dense (lourd) se met au dessous du récipient suivi de l'eau et de huile

Exercice 11 :

Calculer du volume de la partie immergée.

$\begin{array}{rcl} V_{\text{eau}}&=&\rho_{\text{eau}}L1(h-3)\\&=&60\cdot10^{-2}\times(20-3)\cdot10^{-2}\\\Rightarrow\boxed{V_{\text{eau}}=0.0204\,m^{3}} \end{array}$

2 Calculer la masse d'eau déplacée.$\left(\rho_{\text{eau}}=1000\,kg/m^{3}\right)$

$\begin{array}{rcl} m_{\text{eau}}&=&\rho_{\text{eau}}V_{\text{eau}}\\&=&1000\times0.0204\\\Rightarrow\boxed{m_{\text{eau}}=20.4\,kg} \end{array}$

3. Calcul du poids d'eau déplacé

$\begin{array}{rcl} P&=&m_{\text{eau}}g\\&=&20.4\times10\\\Rightarrow\boxed{P=2.04\cdot10^{2}N} \end{array}$

Déduisons la valeur du poids du pavé.

$\begin{array}{rcl} P'&=&P\\&=&2.04\cdot10^{2}N \end{array}$

4. Calcul de la masse du pavé

$\begin{array}{rcl} m_{\text{pavé}}&=&\boxed{m_{\text{eau}}=20.4Kg} \end{array}$

5. a. Calcul du volume du pavé.

$\begin{array}{rcl} V&=&L1h\\&=&60\cdot10^{-2}\times20\cdot10^{-2}\times20\cdot10^{-2}\\\Rightarrow\boxed{V=0.024\cdot m^{3}} \end{array}$

b. Précisons le matériau constituant ce pavé

Déterminons la masse volumique du pavé

$\begin{array}{rcl} \rho&=&\dfrac{m}{V}\\&=&\dfrac{20.4}{0.024}\\\Rightarrow\boxed{\rho=850\,kg\cdot m^{3}} \end{array}$

Le matériau constituant ce pavé est le bois

$\begin{array}{|l|c|c|c|c|c|} \hline \text{Matériau }&\text{Polystyrène }&\text{Bois}&\text{glace }&\text{Aluminium }&\text{Fer }\\ \hline \text{Masse volumique }\left(kg/m^{3}\right)&11&850&920&2700&8000\\ \hline \end{array}$

Exercice 12

Un iceberg a un volume total $V_{T}= 600\;m^{3}$

Sa masse volumique (glace) est $\rho_{1}=910\;kg.m^{-3}$, celle de l'eau de mer est $\rho_{2}=1\,024\;kg.m^{-3}$

1) Schématisons l'iceberg flottant et précisons les forces auxquelles il est soumis lorsqu'il est à l'équilibre.

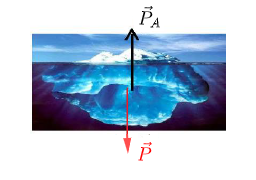
L'iceberg est soumis à son poids $\vec{P}$ et à la force d'Archimède $\vec{P}_{A}.$

2) Calculons la masse totale de l'iceberg.

Soit $m_{T}$ la masse totale de l'iceberg alors, on a :

$$m_{T}=\rho_{1}.V_{T}$$

A.N : $m_{T}=910\times 600=546\,000$

Ainsi, $\boxed{m_{T}=5.46\,10^{5}\;kg}$

3) Calculons le volume immergé (sous l'eau) $V_{i}$ de l'iceberg

La condition d'équilibre s'écrit :

$$\vec{P}+\vec{P}_{A}=\vec{0}$$

Alors, on a :

$\begin{array}{rcl} \vec{P}+\vec{P}_{A}=\vec{0}\\&\Rightarrow&-m_{1}.g+m_{2}.g=0\\\\&\Rightarrow&m_{2}.g=m_{1}.g\\\\&\Rightarrow&m_{2}=m_{1}\\\\&\Rightarrow&\rho_{2}.V_{i}=\rho_{1}.V_{T}\\\\&\Rightarrow&V_{i}=\dfrac{\rho_{1}}{\rho_{2}}V_{T}\\\\&=&V_{i}=\dfrac{910}{1\,024}\times 600\\\\&\Rightarrow&V_{i}=533\end{array}$

D'où, $\boxed{V_{i}=533\;m^{3}}$

4) Trouvons une relation entre le volume immergé $V_{i}$, le volume total $V_{T}$ et les masses volumiques.

En effet, on a : $m_{2}=m_{1}$

Or, $m_{2}=\rho_{2}.V_{i}\ $ et $\ m_{1}=\rho_{1}.V_{T}$

Donc, $\rho_{2}.V_{i}=\rho_{1}.V_{T}$

D'où, $\boxed{V_{i}=\dfrac{\rho_{1}}{\rho_{2}}V_{T}}$

5) En déduisons la proportion (pourcentage) de glace immergée dans cet iceberg.

Soit : $\dfrac{V_{i}}{V_{T}}=\dfrac{533}{600}=0.888$

Donc, on a $89\%$ de glace immergée dans cet iceberg.

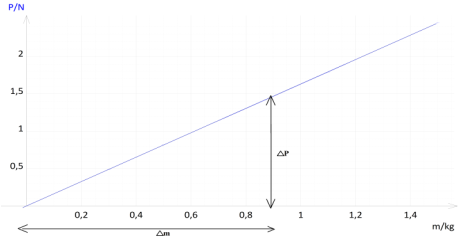
Exercice 13 : Sur la lune

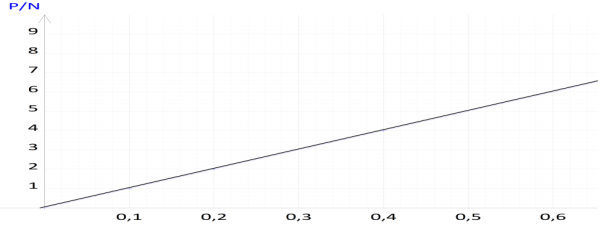
1. Tracé de la courbe traduisant la variation de $P$ en fonction de $m.$

2. Déduisons la valeur de l'intensité de la pesanteur lunaire $g$

$\begin{array}{rcl} g&=&\dfrac{\Delta P}{\Delta m}\\&=&\dfrac{\Delta P-0}{\Delta m-0}\\&=&\dfrac{1.45-0}{0.90-0}\\\Rightarrow\boxed{g=1.6\,N\cdot kg^{-1}} \end{array}$

3. Déduction de la masse de la Lune

$\begin{array}{rcl} g&=&6.67\cdot10^{-11}\dfrac{M}{R^{2}}\\\Rightarrow\;M&=&\dfrac{gR^{2}}{6.67\cdot10^{-11}}\\&=&\dfrac{1.6\times(1738000)^{2}}{6.67\cdot10^{-11}}\\\Rightarrow\boxed{M=7.25\cdot10^{21}kg }\end{array}$

Exercice 14

$\begin{array}{|l|c|c|c|c|c|} \hline \text{Métal }&\text{Fer }&\text{Plomb }&\text{Zinc }&\text{Argent }&\text{Soldat }\\ \hline \text{Masse de l'échantillons }(g)&45&73.5&29.5&76.9&81.4\\ \hline \text{Volume de l'échantillon }(mL)&5.8\,mL&6.5&11&7.3&7.2\\ \hline text{Masse volumique }\left(g\cdot mL^{-1}\right)&7.8&11.3&2.7&10.5&11.3\\ \hline \end{array}$

1. Pour vérifier la composition de ses soldats,François doit déterminer la masse volumique de les tous métaux et comparer ces massiques volumiques avec la masse volumique du soldat

2. L'éprouvette graduée sert à déterminer le volume de chaque échantillon.

Pour déterminer le volume de chaque échantillon, il le plonge dans un récipient gradué contenant une quantité précise d'eau.

En procédant ainsi, il augmente le niveau de l'eau proportionnellement à son volume.

En faisant la différence entre le volume d'eau initiale et le volume final, il trouve le volume du solide

3. Recopions et complétons le tableau en faisant apparaître tous les calculs.

$\begin{array}{rcl} V&=&\dfrac{m}{\rho_{\text{Fer}}}\\&=\dfrac{45}{7.8}\\\Rightarrow\boxed{V=5.8\,mL} \end{array}$ ;

$m=\rho_{V}$ et

$\rho=\dfrac{m}{V}$

4. Le soupçon de François n'est pas avéré, car la masse volumique des ses soldats correspond à la masse volumique du plomb.Ses soldats sont bien en plomb

Auteur:

Sidy Ndiaye

Commentaires

Oumou ly (non vérifié)

lun, 03/22/2021 - 20:05

Permalien

Demande aux auteurs de compléter la correction

Bonjour chers auteurs de ces exercices je vous prie de bien vouloir compléter la correction de l'exercice sur poids , masse, relation entre poids et masse 2nd

répondre

Youssoupha (non vérifié)

lun, 04/19/2021 - 01:43

Permalien

Pourquoi pas complete les

Pourquoi pas complete les exercice

répondre

Alboury (non vérifié)

mar, 05/11/2021 - 13:54

Permalien

Je veux tous les corrections

C'est génial

répondre

Mamadou mouctar... (non vérifié)

ven, 03/03/2023 - 13:40

Permalien

Correction

Je besoin tous les autres correctionsss sur poids et masse et la liaison chimique

répondre

Tabara diop (non vérifié)

mer, 01/10/2024 - 00:49

Permalien