Vous êtes ici

Série d'exercices : Étude du dipôle RC - Ts

Classe:

Terminale

Exercice 1

On veut déterminer la capacité $C$ d'un condensateur, pour cela on réalise sa charge avec un générateur de courant.

Ce générateur débite un courant d'intensité $I=0.5\,mA.$

On réalise la saisie automatique de la tension $U_{C}$ aux bornes du condensateur en fonction du temps.

Le montage utilisé est schématisé ci-dessous :

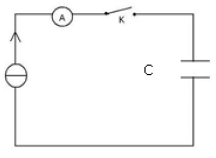
1) Refaire le schéma du montage ; représenter $U_{C}$, $q$ $(q>0)$, la voie $Y$ et la masse de l'oscilloscope afin que l'on puisse visualiser $U_{C}.$

2) A l'instant $t=0$ on ferme l'interrupteur $K.$

Établir la relation entre $I$, $C$, $U_{C}$ et $t.$

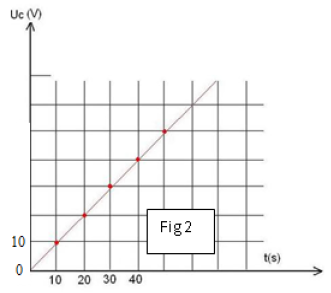
3) On obtient la courbe $U_{C}(t)$ : (voir document ci-dessous).

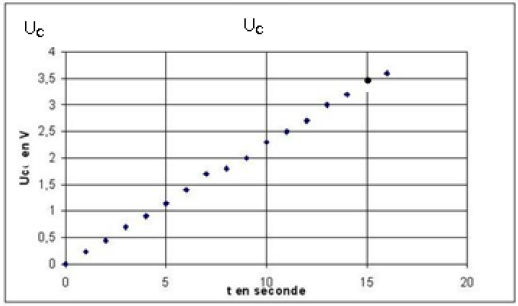
A l'aide de la courbe, déterminer la valeur de la capacité $C$ du condensateur.

4) Afin de ne pas détériorer le condensateur, la durée de charge ne doit pas dépasser $t_{max}=2\,min.$

a) Calculer la tension de claquage du condensateur.

b) Déduire l'énergie électrique maximale emmagasinée par le condensateur.

Exercice 2

Le montage représenté ci-dessous permet de charger et de décharger un condensateur dans une résistance $R.$

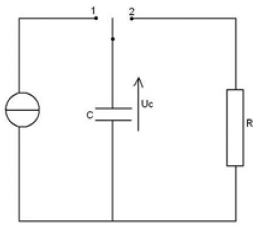
1) a) Pour chacune de ces deux opérations, quelle doit être la position de l'interrupteur ?

1) b) Des deux graphes (fig 1 et fig 2) proposés ci-dessous, lequel correspond à la charge de ce condensateur ?

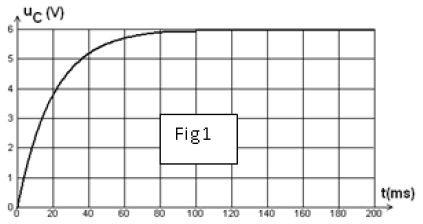
Justifier.

2) Le générateur de courant permet une charge, à intensité constante, d'un condensateur.

La charge dure $40\,s$ et l'intensité du courant a pour valeur $1\mu A.$

2) a) Calculer la charge du condensateur à la date $40\,s.$

2) b) Quelle est la valeur de l'énergie emmagasinée par le condensateur à cette date ?

2) c) Quelle est la capacité du condensateur ?

3) Sachant que ce condensateur est plan et que l'aire des deux surfaces communes en regard est $S=0.1\,m^{2}$ et que l'épaisseur du diélectrique qui se trouve entre les deux plaques est $e=0.02\,mm.$

a) déterminer la permittivité électrique absolue $\epsilon$ du diélectrique de ce condensateur.

b) Déduire la permittivité relative $\epsilon_{r}$ du diélectrique.

On donne $\epsilon_{0}=8.85\cdot10^{-12}u.s.i$

Exercice 3

Le circuit électrique représenté par la figure ci-dessous (fig 2) est constitué des éléments suivants :

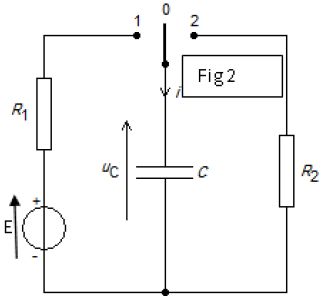
$-\ $ Un générateur de tension idéale de $f.e.m$ $E.$

$-\ $ Deux conducteurs ohmiques de résistances $R_{1}$ et $R_{2}.$

$-\ $ Un condensateur de capacité $C$ initialement déchargé.

$-\ $ Un commutateur $K.$

I. A l'instant $t=0$, on place le commutateur $K$ dans la position 1.

Un système d'acquisition approprié permet d'obtenir les courbes de variation de la charge $q(t)$ du condensateur et la tension $u_{R_{1}}(t)$ aux bornes du résistor $R_{1}.$ (voir fig 3 et fig 4).

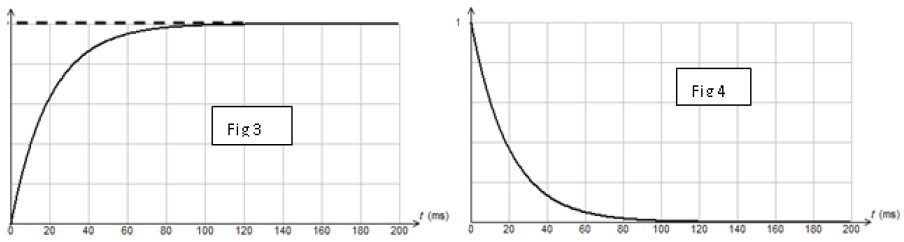
1) a) Préciser, en le justifiant, le graphe correspondant à la charge $q=f(t)$ et celui correspondant à la tension $u_{R_{1}}=g(t).$

b) Établir, à un instant de date $t$ quelconque la relation entre $q$, $u_{R_{1}}$, $E$ et $C.$

c) Montrer qu'à la date $t=0$, la tension $u_{R_{1}}$ est égale à $E.$

En déduire sa valeur $($pour le graphe de $u_{R_{1}}(t)$ : $1$ carreau$\ \longrightarrow\ 2\,V).$

d) A partir du graphe de $q(t)$, prélever la valeur de la charge électrique maximale $Q_{max}$ du condensateur $(1$ carreau$\ \longrightarrow\ 2\cdot10^{-4}C).$

2) a) Définir la constante de temps $\tau$ d'un dipôle $RC.$

Montrer que $\tau$ est un temps.

b) Montrer que l'équation différentielle régissant les variations de $u_{R_{1}}$ au cours du temps peut s'écrire sous la forme $$\tau_{1}\dfrac{\mathrm{d}u_{R_{1}}}{\mathrm{d}t}+u_{R_{1}}=0\text{ avec }\tau_{1}=R_{1}C.$$

c) La solution générale de cette équation est de la forme : $u_{R_{1}}=A\mathrm{e_{-\alpha\;t}}.$

Déterminer $A$ et $\alpha.$

d) Montrer que lorsque le condensateur est complètement chargé, sa tension est égale à $E.$

Déduire la valeur de la capacité $C.$

3) a) Déterminer graphiquement $\tau_{1}.$

Préciser la méthode utilisée.

b) Calculer la valeur de $R_{1}.$

c) Calculer l'énergie électrique emmagasinée dans le condensateur lorsque $u_{R_{1}}=u_{C}.$

II. Lorsque le condensateur est complètement chargé, on bascule le commutateur $K$ à la position $2$ à un instant choisi comme nouvelle origine des dates.

1) a) Écrire la loi des mailles correspondante.

b) Montrer qu'à la date $t=0$, la tension aux bornes du résistor $R_{2}$ est $u_{R_{2}}=-E.$

2) La tension aux bornes du résistor $R_{2}$ est donnée par l'expression $u_{R_{2}}=-E\cdot \mathrm{e^{-t/\tau_{2}}}$ avec $\tau_{2}=R_{2}C.$

a) Sachant qu'à la date $t_{2}=4\cdot10^{-2}s$, la charge du condensateur est $q=3.7\cdot10^{-4}C.$

Calculer $R_{2}.$

b) Représenter sur le même graphe l'allure de la courbe représentant $q$ en fonction du temps au cours de la décharge.

Même question pour la tension $u_{R_{2}}(t).$

Exercice 4

Au cours d'une séance de $TP$ on étudie la décharge d'un condensateur de capacité $C$ (préalablement chargé) à travers un dipôle ohmique de résistance $R.$

Un ordinateur muni d'une interface et d'un tableur a permis de tracer les courbes représentant l'évolution de la tension $u=u_{AB}$ et de l'intensité du courant dans le circuit (voir ci-dessous).

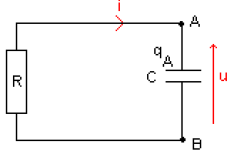
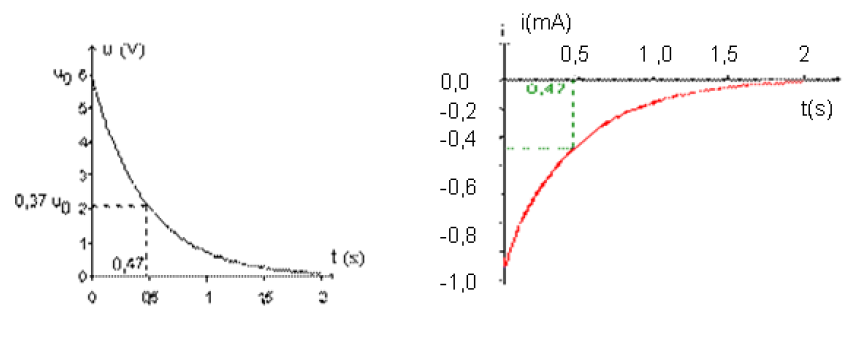
1) Établir la relation entre $i$ et $\dfrac{\mathrm{d}u}{\mathrm{d}t}.$

2) Donner, en justifiant la réponse, le signe de $q_{A}$ à l'instant $t=0.$

3) Indiquer, en justifiant les réponses, le sens réel du courant et le sens de déplacement des électrons.

4) Déterminer la valeur de la constante de temps $\tau$ du dipôle $RC.$

5) Déterminer les valeurs de $R$ et de $C.$

Exercice 5

On étudie le flash d'un appareil photographique jetable.

Dans ce type d'appareil, une pile de $1.5V$ alimente un oscillateur.

Un transformateur élève la tension qui, après avoir été redressée, permet de charger un condensateur.

Une lampe témoin s'allume lorsque le flash est prêt à fonctionner.

La décharge du condensateur dans une lampe à éclat engendre l'éclair.

Le condensateur utilisé porte les indications suivantes : $330\,V$ ; $160\mu F\pm;10\%.$

La durée minimale séparant deux déclenchements successifs du flash est de $10\,s.$

Pour vérifier la valeur de la capacité du condensateur, on réalise le montage schématisé ci-dessous.

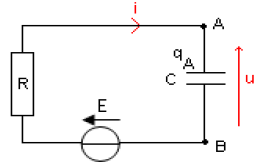
Le condensateur, initialement déchargé, est alimenté à travers un dipôle ohmique de résistance $R=12.5k\Omega$ par une source idéale de tension appliquant une tension $E=300\,V.$

A l'aide d'un oscilloscope numérique, on visualise la tension $u_{C}$ aux bornes du condensateur ainsi que la tension $u_{R}$ aux bornes du dipôle ohmique.

Ces courbes sont représentées ci-dessous.

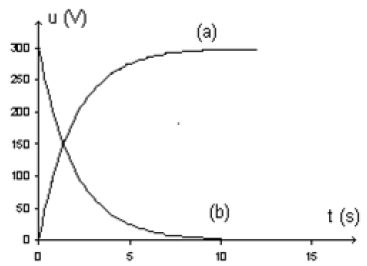
1) Indiquer, sur le schéma du montage, le branchement permettant à un oscilloscope de tracer les courbes (a) et (b).

On précisera sur le schéma les tensions effectivement mesurées.

2) Des tensions $u_{R}$ et $u_{C}$, quelle est celle qui permet de suivre l'évolution du courant (intensité) dans le circuit ?

Justifier la réponse.

3) Quelle est des deux courbes (a) et (b) celle qui représente $u_{C}$ ?

Justifier la réponse.

4) Montrer que le produit $R_{C}$ est homogène à une durée.

5) Montrer qu'une seule des équations différentielles suivantes est correcte.

$$(1)\quad R\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+Cu_{R}=0\ ;$$

$$(2)\quad C\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+Ru_{R}=0\ ;$$

$$(3)\quad RC\dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+u_{R}=0\ ;$$

$$(4)\quad \dfrac{\mathrm{d}u_{R}}{\mathrm{d}t}+RCu_{R}=0\ ;$$

6) La solution de l'équation différentielle vérifiée par la tension $u_{R}$ a pour expression : $u_{R}=E\mathrm{e^{-t/\tau}}$ avec $\tau=RC.$

Montrer que l'on peut écrire : $Ln(u_{R})=at+b.$

On exprimera $a$ et $b$ en fonction de $E$ et $\tau.$

7) La droite précédente est tracée par l'ordinateur (document ci-dessous).

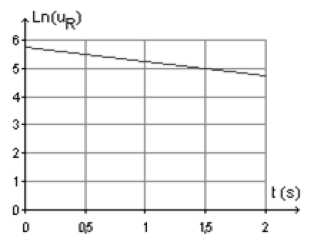
En déduire la valeur de la capacité $C$ du condensateur.

Cette valeur est-elle en accord avec l'indication portée sur le condensateur ?

Exercice 6

1. On considère le circuit électrique ci-dessous comprenant un conducteur ohmique de résistance $R=4.7\,k\Omega$, un condensateur de capacité $C$ et une alimentation stabilisée de tension à vide $E.$

Un fil conducteur relie les bornes $B$ et $D$ du condensateur.

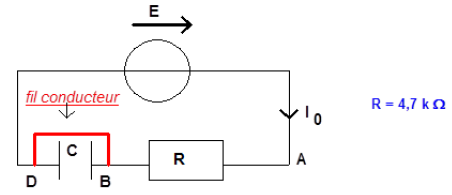
1.1 Que vaut la tension aux bornes du condensateur ?

1.2 Déterminer l'expression de l'intensité $I_{0}$ du courant dans le circuit en fonction de certains paramètres parmi les suivants $E$, $R$, $C.$

2. On se propose de suivre l'évolution de la tension $u_{BD}$ aux bornes du condensateur, au cours du temps.

Un ordinateur est relié au circuit électrique par l'intermédiaire d'une interface d'acquisition de données (voir figure 1)

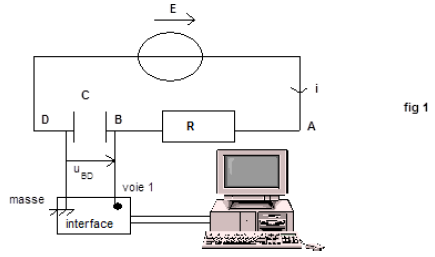
A la date $t=0$, on enlève le fil conducteur aux bornes du condensateur.

On enregistre alors la variation de la tension $u_{BD}$ aux bornes du condensateur au cours du temps.

L'acquisition de mesures étant terminée, on trace le graphe d'équation $u_{BD}=f(t)$ (voir document 1).

2.1 Déterminer, à partir du document 1, la valeur de la tension $E.$

En déduire la valeur de l'intensité $I_{0}$ du courant dans le circuit à $t=0.$

2.2 Établir que l'équation différentielle d'évolution de la tension $u_{BD}$ au cours du temps est donnée par l'expression :

$$\boxed{\dfrac{\mathrm{d}u_{BD}}{\mathrm{d}t}+\dfrac{u_{BD}}{RC}=\dfrac{E}{RC}}$$

Vérifier à partir de l'équation différentielle que la constante de temps du circuit $\tau=RC$ est homogène à une durée.

2.3 A partir du coefficient directeur de la tangente $(T)$ à la courbe $u_{BD}=f(t)$ à l'instant de date $t=0$, déterminer la constante de temps du circuit.

En déduire la valeur de la capacité $C$ du condensateur.

A partir du document 1, déterminer la durée au bout de laquelle on peut considérer que le condensateur est chargé.

Comparer cette durée à la constante de temps $\tau$ du circuit.

3. On désire visualiser sur un oscilloscope l'évolution de la tension $u_{BD}$ aux bornes du condensateur lors de sa charge.

Le circuit électrique comprend maintenant un générateur basse fréquence $(GBF)$ délivrant une tension carrée $u_{AD}$, un condensateur de capacité $C'=10\,nF$ et un conducteur ohmique de résistance $R'=10\,k\Omega.$ (fig 2).

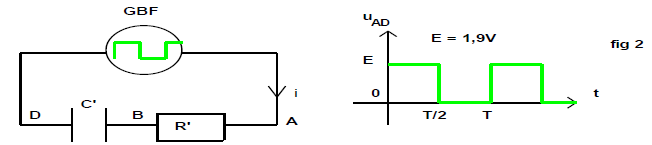
4. Indiquer, sur le circuit électrique de la figure 2, les branchements à réaliser pour visualiser sur la voie 1 de l'oscilloscope la tension délivrée par le générateur basse fréquence, et sur la voie 2 la tension aux bornes du condensateur.

Exercice 7

I. On se propose d'étudier l'évolution de la tension aux bornes d'un condensateur dans le but de déterminer la capacité du condensateur.

Un générateur de tension de force électromotrice $E$ alimente un conducteur ohmique de résistance $R=100\Omega$ et un condensateur de capacité $C$, associés en série (figure 1).

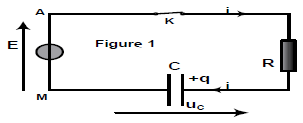
Un dispositif d'acquisition de données relié à un ordinateur permet de suivre l'évolution de la tension $u_{C}$ aux bornes du condensateur en fonction du temps.

À la date $t=0$, on ferme l'interrupteur $K$ et l'ordinateur enregistre la courbe $u_{C}=f(t).$

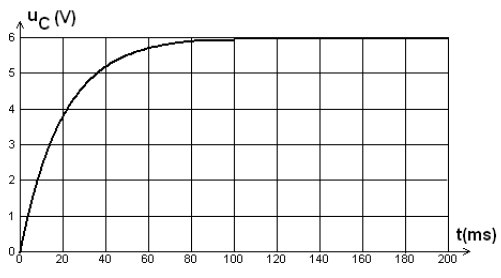
1) À l'aide de la courbe $u_{C}(t)$, déterminer la date $t$ à partir de laquelle on peut considérer que la tension $u_{C}$ est constante.

Quel phénomène physique est mis en évidence par la portion de courbe située avant la date $t$ ?

2) Déterminer la valeur de $E.$

Expliquer.

3) Déterminer la valeur de la constante de temps $\tau$ du circuit.

4) En déduire une valeur approchée de $C.$

5) Évaluer, à partir de la figure ci-dessus, la durée $\Delta\;t$ nécessaire pour charger complètement le condensateur.

Comparer $\Delta\;t$ à $\tau.$

6) Faut-il augmenter ou diminuer la valeur de $R$ pour charger plus rapidement le condensateur ?

Justifier la réponse.

7) En respectant l'orientation d'intensité qui est indiquée sur la figure 1, établir l'équation différentielle vérifiée par la tension $u_{C}.$

8) Sachant que $u_{C}=E\left(1-\mathrm{e^{-t/RC}}\right)$ est solution de l'équation différentielle et en respectant l'orientation d'intensité qui est indiquée sur la figure 1, établir l'expression de $i(t).$

En déduire l'allure de la courbe $i=f(t).$

Exercice 8

On dispose au laboratoire d'un condensateur de capacité $C$ inconnue, pour déterminer expérimentalement la valeur de $C$, deux groupes d'élèves proposent deux solutions différentes.

I. Le premier groupe réalise un circuit électrique comportant :

$\ast\ $ Un générateur idéal de courant débitant un courant d'intensité constante $I=20\mu A.$

$\ast\ $ Un voltmètre.

$\ast\ $ Le condensateur de capacité $C$ inconnue.

$\ast\ $ Un conducteur ohmique de résistance $R$

$\ast\ $ Un interrupteur $K$ et un chronomètre.

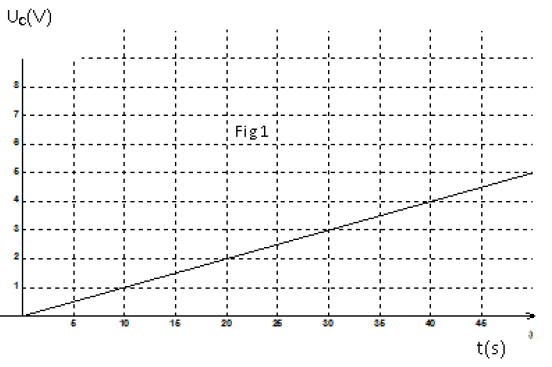
A la date $t=0$, ils ferment l'interrupteur $K$ et mesurent à différentes dates la tension aux bornes du condensateur, ce qui leur a permis de tracer la courbe de variation de la tension $u_{c}$ aux bornes du condensateur en fonction du temps (figure 1 ).

1) Représenter le schéma du circuit en indiquant le branchement du voltmètre.

2) Établir l'expression de $u_{C}$ en fonction de $I$, $C$ et $t.$

3) Déterminer graphiquement la valeur de la capacité $C.$

Calculer à la date $t=20\,s$, l'énergie emmagasinée dans le condensateur.

II. Le deuxième groupe réalise un circuit électrique comportant :

$-\ $ Un générateur basse fréquence $G.B.F$ de signaux carrés, de fréquence $N$, fournissant alternativement une tension nulle ou positive $U_{m}$ (Tension créneaux).

$-\ $ Un oscilloscope bicourbe,

$-\ $ Le condensateur de capacité $C$ inconnue.

$-\ $ Un conducteur ohmique de résistance $R$ réglable et un interrupteur $K.$

1) Représenter le schéma du circuit en indiquant les branchements des fils de masse et les entrées $Y_{A}$ et $Y_{B}$ de l'oscilloscope nécessaire pour visualiser respectivement la tension fournie par le $G.B.F$ et la tension aux bornes du condensateur.

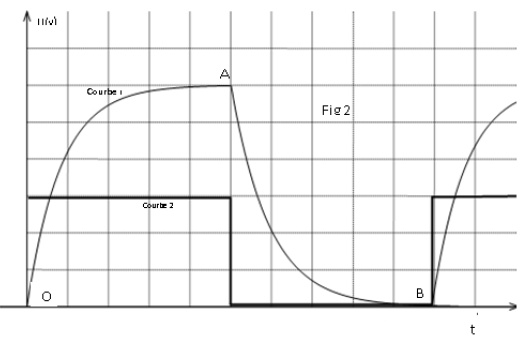
2) Avec $R=40\Omega$, on observe sur l'écran de l'oscillo les courbes de la figure 2.

Les réglages de l'oscilloscope indiquent Sensibilité verticales sur $Y_{A}$ : $2V\cdot div^{-1}$ et sur $Y_{B}$ : $1V\cdot div^{-1}.$

Sensibilité horizontale : $10\,ms\cdot div^{-1}.$

a) Identifier les courbes 1 et 2, interpréter le phénomène observé principalement, dans les zones $OA$ et $AB.$

b) Établir l'équation différentielle régissant les variations de $u_{C}$ dans la zone $OA.$

Donner l'expression de sa solution en fonction de $U_{m}$, $R$, $C$ et $t.$

c) Déterminer graphiquement

$-\ $ La période $T$ du $G.B.F$ et la tension maximale $U_{m}$ fournie.

Calculer la fréquence $N.$

$-\ $ la constante de temps $\tau.$

Déduire la valeur de la capacité $C$ du condensateur, la comparer à celle trouvée par le premier groupe.

d) Tracer sur le même graphe l'allure de la courbe de variation de la tension $u_{R}$ aux bornes du résistor en fonction du temps.

Préciser sur le graphe les deux régimes.

3) On règle la résistance $R$ à la valeur $60\Omega.$

a) Calculer la nouvelle valeur de la constante de temps.

Tracer, sur le même graphe, l'allure de la courbe représentant $u_{C}$ en fonction du temps.

Exercice 9

I. Le condensateur de capacité $C$ utilisé dans le montage schématisé ci-dessous est alimenté par un générateur de tension supposé idéal délivrant entre ses bornes une tension $E=6V.$

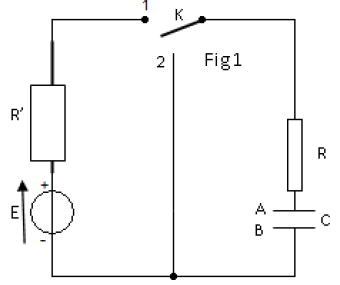
Un conducteur ohmique a une résistance $R=300\Omega$ alors que l'autre sa résistance $R'$ est inconnue.

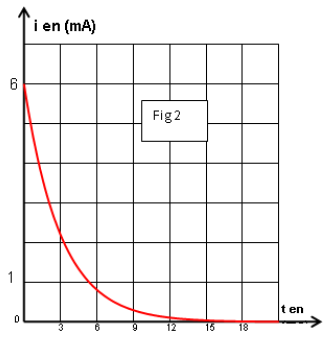
Le condensateur étant initialement déchargé, le commutateur $K$ est placé sur la position $1$ à un instant pris comme origine de temps et à l'aide d'un ordinateur muni d'une interface on a pu suivre l'évolution de l'intensité de courant électrique dans le circuit voir figure 2 (page à compléter et à remettre avec la copie)

1) En désignant par $q$ la charge positive portée par l'armature $A$ du condensateur à une date $t.$

Indiquer sur le schéma le sens arbitraire positif du courant $i(t).$

2) En appliquant la loi des mailles, établir l'équation différentielle régissant les variations de l'intensité du courant $i(t).$

3) Cette équation différentielle admet pour solution : $i(t)=A\cdot\mathrm{e^{-\alpha\;t}}$ où $A$ et $\alpha$ sont deux constantes positives qu'on déterminera leurs expressions.

4) Déterminer l'expression de la tension aux bornes du condensateur $u_{AB}(t).$

5) En utilisant le graphe de $i(t)$, déterminer :

a) la valeur de la résistance $R'.$

b) la valeur de la constante de temps $\tau.$

Déduire la valeur de la capacité $C.$

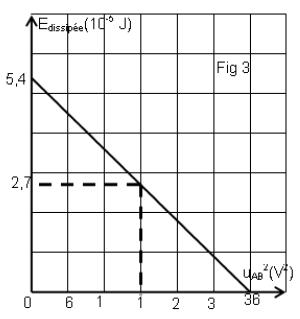
II. Lorsque l'intensité de courant s'annule dans le circuit, on bascule le commutateur $K$ sur la position $2$ à une date considérée comme origine de temps alors qu'on a programmé l'ordinateur pour tracer la courbe d'évolution de l'énergie dissipée dans le résistor $R$ en fonction de $u_{AB}^{2}.$

La courbe obtenue est donnée par la figure 3