Vous êtes ici

Série d'exercices : Équilibre d'un solide mobile autour d'un axe - 2nd S

Classe:

Seconde

Exercice 1

Un chemin forestier est fermé par une barrière constituée d'une poutre (1) et d'un contre-poids (2).

La barrière peut tourner autour d'un axe $\Delta$ perpendiculaire en $O$ au plan de la figure

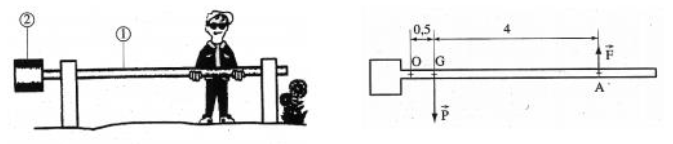
Les cotes sont en mètres. La masse de la barrière est $60\;kg\;;\ G$ est son centre de gravité.

Un promeneur veut la soulever en exerçant en $A$ une force $\vec{F}$ d'intensité $100\;N.$

1) Calculer :

a) l'intensité du poids $\vec{P}$ de la barrière. On donne : $g=10\;N.kg^{-1}.$

b) le moment de $\vec{P}$ par rapport à $\Delta.$

c) le moment de $\vec{F}$ par rapport à $\Delta.$

2) Le promeneur peut-il soulever la barrière ? Justifier la réponse

Exercice 2

Le chargeur représenté ci-dessous se compose:

$-\ $ d'un châssis et du conducteur de masse $400\;kg$ ;

$-\ $ de son chargement de masse $420\;kg$ ;

$-\ $ d'un système de levage et du godet de masse $150\;kg.$

Le poids du châssis s'applique au point $G_{1}$

Le poids du chargement au poing $G_{2}$

Le poids du système de levage au poing $G_{3}$

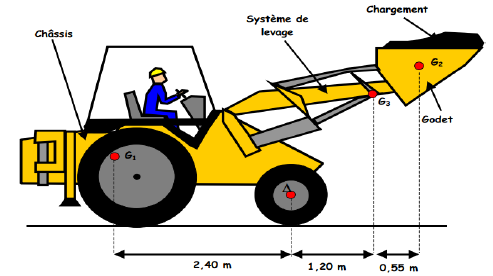
1) Calculer les intensités des poids du châssis, $P_{1}\;,\ P_{2}\ $ et $\ P_{3}$ , du chargement et du système de levage

2) Calculer le moment du poids $P_{1}$ par rapport à l'axe $\Delta$ de la roue avant.

3) Calculer le moment du poids $P_{2}$ par rapport à l'axe $\Delta$ de la roue avant.

4) Calculer le moment du poids $P_{3}$ par rapport à l'axe $\Delta$ de la roue avant.

5) Le chargeur ainsi chargé pivote-t-il autour de l'axe $\Delta\ ?$

6) Quelle est la charge maximale que peut transporter le godet

Exercice 3

Un solide $(S)$ de masse $m=200\;g$ est relié à un fil de masse négligeable passant par la gorge d'une poulie à axe fixe $(\Delta)$, de masse négligeable et de rayon $r.$

L'autre extrémité du fil est attachée à un ressort de raideur $k$ et de masse négligeable.

A l'équilibre, l'axe du ressort fait un angle $\alpha=30^{\circ}$ avec l'horizontale et le ressort est allongé de $\Delta l=4\;cm.$ On néglige tout type de frottement.

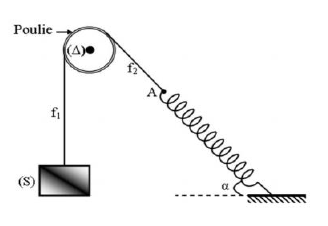
1) a) Représenter les forces exercées sur le solide $(S).$

b) Écrire la condition d'équilibre de $(S)$ et déterminer l'expression de la tension du fil $f_{1}$, puis calculer sa valeur.

2) a) Représenter les forces exercées sur la poulie.

b) En appliquant le théorème des moments, déterminer la tension du fil $f_{2}$

c) Déduire la tension du fil $f_{2}$ au point $A.$

3) Déterminer la valeur de la raideur du ressort $k$

4) Par projection de la relation vectorielle, traduisant l'équilibre de la poulie, dans un repère orthonormé, montrer que la valeur de la réaction $R$ de l'axe ($\Delta$) est $R=mg\sqrt{2(1+\sin\alpha)}$

Calculer sa valeur.

On prendra : $g=10\;N.kg^{-1}$

Exercice 4

On dispose d'une règle homogène, de masse négligeable, pouvant tourner autour d'un axe horizontal $\Delta$ passant par son centre d'inertie $O.$ On veut connaître le comportement de la règle dans les situations suivantes

1) La règle, initialement au repos, est soumise à un seul couple de forces $(\vec{F}\;,\ \vec{F'})\ :$

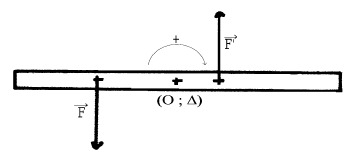
Indiquer quel est le comportement de la règle et donner le signe du moment du couple de forces.

2) La règle, initialement au repos, est soumise à deux couples de forces $(\vec{F}_{1}\;,\ \vec{F}_{2})\ $ et $\ (\vec{F}_{3}\;,\ \vec{F}_{4})$ tels que

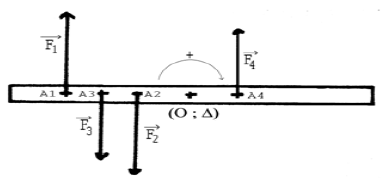
Échelle : $1\;cm\longleftrightarrow 2\;N\ $ et $\ 1\;cm\longleftrightarrow10\;cm$

2.1) Calculer le moment de chaque couple.

2.2) Exprimer la condition d'équilibre de la règle.

Montrer alors que la règle n'est pas en équilibre mais en rotation non uniforme.

Préciser dans quel sens se fait cette rotation.

2.3) On veut obtenir l'équilibre de cette règle :

2.3.1) Pour cela, on déplace le point d'application $A_{3}$ de la force $\vec{F}_{3}$

Déterminer la position de $A_{3}$ par rapport à $O$ pour que la règle soit en équilibre.

2.3.2) Le point $A_{3}$ reprend sa position initiale : $OA_{3}=0.20\;m$ et on incline les forces $\vec{F}_{3}\ $ et $\ \vec{F}_{4}$ d'un angle $\alpha$ par rapport à la verticale comme le montre le schéma ci-dessous.

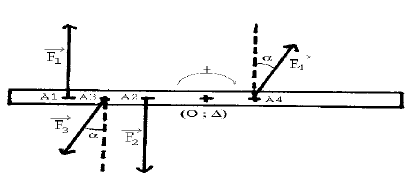
Donner l'expression du moment du couple $(\vec{F}_{3}\;,\ \vec{F}_{4})$ en fonction de $\alpha\;,\ F_{3}\;,\ A_{3}A_{4}$

Déterminer la valeur de $\alpha$ pour laquelle la règle est en équilibre

Exercice 5

Une tige rigide et homogène $(AB)$ de longueur $L$, de masse M peut tourner sans frottement autour d'un axe fixe ($\Delta$) horizontal qui lui est orthogonal passant par le point $O$ (voir figure 2).

Pour maintenir la tige $AB$ en équilibre suivant une direction faisant un angle $\alpha=30^{\circ}$ avec la verticale,

on fixe à son extrémité B un ressort à aspires non jointives , de masse négligeable et de raideur $K=10\;N.m^{-1}\;;\ OA=\dfrac{L}{4}$

L'axe de ressort maintenu horizontal. On donne :

On se propose d'étudier l'équilibre de la tige $AB.$

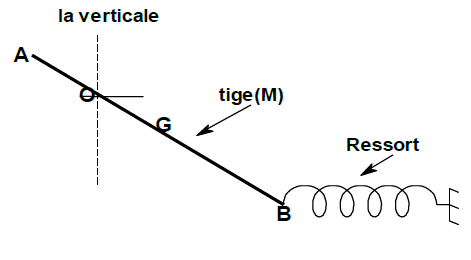
1) Représenter toutes les forces extérieures appliquée à la tige $AB.$

2) Donner l'expression de moment de chaque force par rapport à l'axe de rotation $(\Delta)$ passant par le point $O.$

3) Par application du théorème des moments à la tige $AB$ en équilibre ,

Établir l'expression de la tension du ressort exercée à l'extrémité $B$ en fonction de : $M\;,\ g\ $ et $\ \alpha$

4) A l'équilibre, le ressort s'allonge de $x=5\;cm.$

Calculer la tension du ressort.

En déduire la masse $M$ de la tige $AB.$ On prendra $g=10\;N.kg^{-1}$

5. a) Calculer la réaction de l'axe $(\delta)$ en $O.$

b) Déterminer l'angle $\beta$ que fait la direction de la réaction avec la verticale.

Exercice 6

Une barre homogène de longueur $L=AB=60\;cm$ et de masse $m=2\;kg$ peut tourner autour de son extrémité $A.$

Un fil horizontal fixé en B maintient la barre en équilibre.

La barre fait le plan horizontal un angle de $\alpha=15^{\circ}$

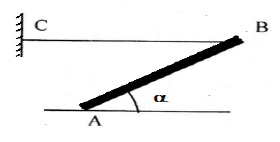
1) Représenter les forces qui s'exercent sur la barre

2) calculer l'intensité de la force exercée par le fil $BC$ sur la barre.

3) Déterminer les caractéristiques de.la réaction du sol sur la barre.

Exercice 7

On considère le dispositif suivant, il est formé par :

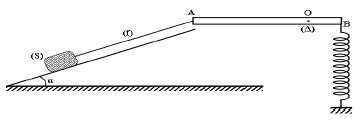
$-\ $ Une tige $AB$ de longueur $L$, de masse négligeable et mobile autour d'un axe fixe ($\delta$) placé au point $O$ (perpendiculaire au plan de la figure), tel que $OB=\dfrac{L}{4}$

$-\ $ Un ressort de raideur $k=30\;N.m^{-1}$, de masse négligeable et perpendiculaire à la tige au point $B$ où il est attaché.

$-\ $ Un solide $(S)$ de masse $400\;g$, posé sur un plan incliné de $\alpha=30^{\circ}$ par rapport à l'horizontale, et en équilibre grâce à un fil $(f)$ attaché à l'extrémité $A$ de la tige.

Le plan est supposé lisse.

$-\ $ On prendra $g=10\;N.kg^{-1}$

1) a) Représenter les forces extérieures qui s'exercent sur le solide $(S)$ à l'équilibre.

b) Écrire la condition d'équilibre du solide $(S).$

c) Étudier cet équilibre et déterminer l'expression de la tension $T$ du fil $(f)$ en fonction de $m\;,\ g\ $ et $\ \alpha$

d) Calculer la valeur de $T$

2) a) Représenter les forces extérieures qui s'exercent sur la tige $AB$ à l'équilibre.

b) Écrire la condition d'équilibre, traduite par le théorème des moments, de la tige $AB.$

c) Donner l'expression du moment de chacune de ces forces.

d) Déduire l'expression de la tension $T_{B}$ du ressort au point $B$ en fonction de $m\;,\ g\ $ et $\ \alpha$

e) Calculer la valeur de $T_{B}$

h) Déduire l'allongement $\delta l$ du ressort.

3) a) Écrire la deuxième condition d'équilibre de la tige.

b) Étudier cet équilibre et déterminer la valeur de la réaction R de l'axe $(\delta)$ ainsi que celle de l'angle $\beta$ que fait la réaction avec la verticale

Exercice 8

Une tige rigide et homogène de longueur L et de masse $M=500\;g$, est suspendue par l'une de ses extrémités, notée $O$, à un axe $(\delta)$ horizontal qui lui est perpendiculaire et autour duquel elle peut tourner sans frottement .

On maintient la tige en équilibre suivant une direction faisant avec la verticale un angle $\alpha=30^{\circ}.$

L'équilibre est assuré à l'aide d'un fil de masse négligeable lié à l'extrémité libre $A$ de la tige et tendu horizontalement à l'autre extrémité du fil qui passe à travers la gorge d'une poulie on accroche un solide de masse $m$ (voir figure 1).

On néglige toutes les forces de frottement.

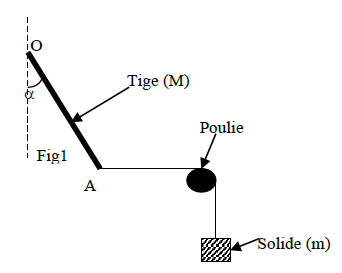
1) Quelles sont les forces extérieures appliquées à la tige ? Les représenter.

2)a) A l'aide du théorème des moments appliqué à la tige en équilibre, établir l'expression de la tension du fil appliquée au point $A$ en fonction de : $M\;,\ g\ $ et $\ \alpha.$

b) En déduire l'expression de la masse $m$ du solide. Calculer sa valeur.

Déterminer la valeur de la réaction de l'axe sur la tige en $O$ ainsi que l'angle $\beta$ qu'elle fait avec la verticale.

Exercice 9

On utilise dans cet exercice

$-\ $ Une sphère métallique homogène, de rayon $r=3\;cm$, de masse $M=1\;kg$

$-\ $ Une tige métallique de longueur $L=47\;cm$ ,très fine ,dont la masse est négligeable devant celle de la sphère. On prendra $g=10\;N.Kg^{-1}.$

On soude la tige à la sphère .Le dispositif ainsi constitué peut tourner, dans le plan vertical, autour d'un axe $(\delta)$, horizontal, passant par l'extrémité $O$ de la tige.

En un point $A$ de la tige, tel que : $OA=a=40\;cm$ on fixe un fil que l'on supposera toujours vertical.

Lorsque le système est en équilibre la tige fait un angle $\alpha$ avec l'horizontale.

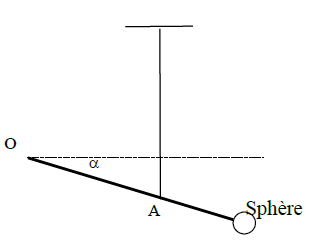
1) Représenter les forces exercées la tige à l'équilibre.

2) Par application du théorème des moments, établir l'expression de la tension du fil $T_{A}$ du fil appliquée en $A.$

Calculer sa valeur.

3) Déterminer la réaction $R$ de l'axe en $O.$

4) On remplace maintenant le fil par un ressort de raideur $K$ et de masse négligeable.

Ce ressort que l'on supposera toujours vertical n'est pas tendu lorsque la tige est horizontale.

Lorsque le système est en équilibre la tige fait un angle $\Theta=6^{\circ}$ avec l'horizontale.

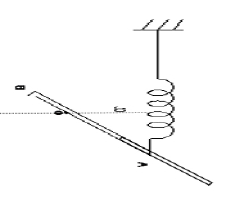
Calculer l'allongement du ressort à l'équilibre

En déduire la raideur $K$ du ressort.

Exercice 10

On suspend des poids différents à des distances variables afin que le système soit en équilibre et on note les résultats obtenus.

Expérience :

$m_{1}=800\;g\;;\ m_{2}=400\;g$

$d=1.5\;cm\;;\ D=3\;cm$

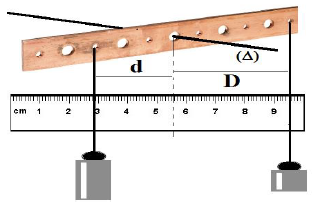
1) Faire le bilan des actions s'exerçant sur la barre à trous.

2) Sur la figure ci-dessus, tracer la direction de ces forces.

3) Déterminer les caractéristiques de ces forces lorsque cela est possible.

4) Calculer le moment de chaque force

5) Calculer la somme des moments des forces s'exerçant sur la une barre à trous

Exercice 11

On donne $g=10\;N.Kg^{-1}$

Une tige $AB$ de masse $m$, de longueur $L=60\;cm$, homogène, de section constante, mobile autour d'un axe horizontal ($\delta$) orthogonal à la tige passant par son extrémité $A.$

A son extrémité $B$ on exerce une force $F_{B}$ de même direction que la tige et de valeur $4\;N.$

Au point $C$ tel que $AC=\dfrac{L}{4}$ est appliquée une force $F_{C}$ de direction verticale dirigée vers le haut et de valeur $6\;N$ (Voir figure)

1.1) Faire le bilan des forces extérieures exercées sur la tige.

1.2) Calculer la valeur algébrique des moments par rapport à l'axe $\delta$ des forces $F_{B}\ $ et $\ F_{C}.$

2) Sachant que la tige est en équilibre dans cette position.

2.1) Calculer la valeur algébrique du moment du poids par rapport à l'axe $\delta.$

2.2) Déduire la masse $m$ de la tige.

3) La direction de la force $F_{B}$ fait maintenant un angle $\alpha=30^{\circ}$ avec celle de la tige (Voir figure 2).

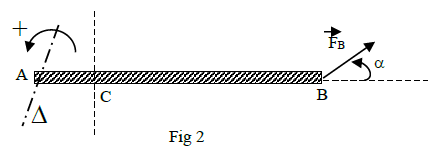
Que deviennent le sens et la valeur de la force $F_{C}$ pour que la tige garde la même position d'équilibre.

Exercice 12

Le schéma ci-dessous représente un cabestan (treuil) : il est constitué de deux manivelles solidaires d'un tambour $(t)$ d'axe $O$, sur lequel s'enroule un câble tendu.

Les mains exercent, aux extrémités des manivelles, deux forces $F_{1}\ $ et $\ F_{2}$ parallèles et de même intensité $100\;N$

Le câble exerce, en $A$, sur le tambour, une force $\vec{F}_{c/t}$ verticale.

l'ensemble des autres forces d'exerçant sur le treuil est équivalent à une force $R$ exercée en $O.$

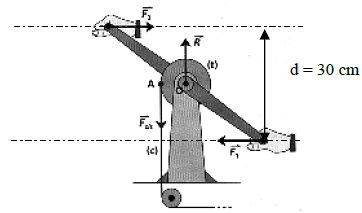
1) Quel est le moment de la force $\vec{R}$ par rapport à $O\ ?$

2) Calculer le moment du couple $(\vec{F_{1}}\;,\ F_{2})$

3) Sachant que le treuil est en équilibre dans cette position, en déduire l'intensité de la force exercée par le câble tendu sur le tambour (on donne $OA=6.5\;cm)$

Exercice 13

I Un mobile est constitué de 3 poulies solidaires entre elles pouvant tourner autour du même axe.

On attache un fil à chaque poulie et une masse.

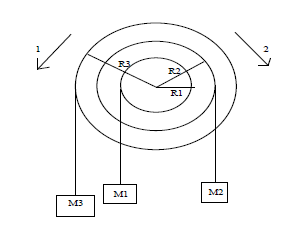
$$M_{1}=200\;g\quad R_{1}=5\;cm$$

$$M_{2}=300\;g\quad R_{2}=10\;cm$$

$$M_{3}=100\;g\quad R_{3}=16\;cm$$

1) Le solide est il en équilibre ?

$\ast\ $ S'il ne l'est pas, dans quel sens tourne t-il ? 1 ou 2 ? Pourquoi ?

2) Par quelle masse devrait-on remplacer $M_{2}$ pour qu'il soit en équilibre ?

3) Si $M_{2}$ était toujours égale à $300\;g$, à quelle distance de l'axe $R_{3}$ devrait-on attacher $M_{3}$

Exercice 14

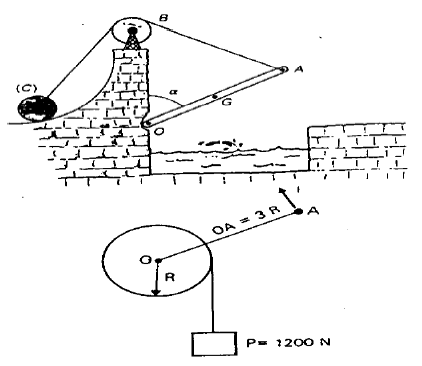
1) Le pont-levis est mobile autour de l'axe horizontal $O.$ Il est constitué d'un plateau de poids $P=5000\;N$ et dont le centre d'inertie $G$ est au milieu de $OA.$

Il est maintenu en équilibre, dans la position correspondant à $\alpha=60^{\circ}$, grâce au contre poids $C$ et à la corde $ABC$ dont on néglige la masse. $OA=OB=4\;m.$

Calculer la tension $T$ de la corde dans ces conditions, puis sa tension $T'$ lorsque le pont est abaissé mais sans reposé.

2) Soit un treuil de masse $M=20\;kg$ ; il permet de soulever une charge de $1200\;N.$

Déterminer le module de la force $F$ qu'il faut exercer perpendiculairement à $OA$ pour soulever la charge

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur:

Sidy Mouhamed Ndiaye

Commentaires

Fallou Biteye (non vérifié)

sam, 06/19/2021 - 10:19