Vous êtes ici

Solution des exercices : Droites remarquables - 4e

Classe:

Quatrième

Exercice 1

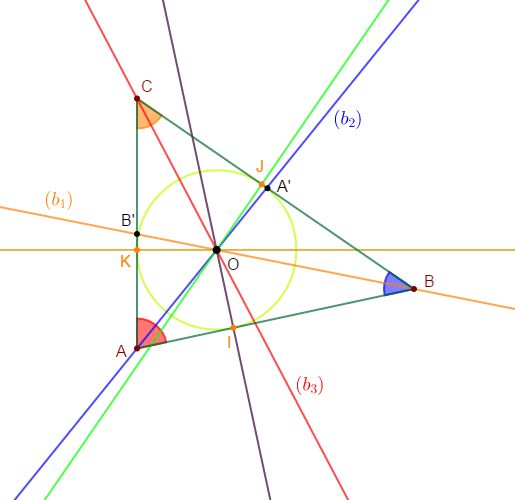
1) Construisons un triangle

$ABC$ quelconque.

2) a) Construisons la droite

$(b_{2})$ bissectrice de l'angle

$\widehat{A}$ ; elle coupe

$(BC)$ en

$A'.$

b) Construisons la droite

$(b_{1})$ bissectrice de l'angle

$\widehat{B}$ ; elle coupe

$(AC)$ en

$B'.$

3) a)

$(b_{1})\$ et

$\ (b_{2})$ se coupent en

$O$ , marquons

$O.$

4) a) La droite perpendiculaire à

$(AB)$ et passant par

$O$ coupe la droite

$(AB)$ en

$I.$

b) La droite perpendiculaire à

$(BC)$ et passant par

$O$ coupe la droite

$(BC)$ en

$J.$

c) La perpendiculaire à

$(AC)$ et passant par

$O$ coupe la droite

$(AC)$ en

$K.$

5) a) Démontrons que :

$OI=OJ=OK$

En effet, on sait que Si un point

$M$ appartient à la bissectrice d'un angle alors, il est équidistant des supports des deux côtés de l'angle.

Or,

$O\in(b_{1})$ bissectrice de l'angle

$\widehat{B}$ donc,

$O$ est équidistant des supports des deux côtés de l'angle

$\widehat{B}.$

C'est-à-dire ;

$d(O\;,\ (AB)=d(O\;,\ (BC)$

Comme,

$d(O\;,\ (AB)=OI\$ et

$\ d(O\;,\ (BC)=OJ$ alors, on obtient :

$OI=OJ$

De même, le point

$O$ appartient à

$(b_{2})$ bissectrice de l'angle

$\widehat{A}$ donc,

$O$ est équidistant des supports des deux côtés de l'angle

$\widehat{A}.$

Ce qui signifie :

$d(O\;,\ (AB))=d(O\;,\ (AC))$

Or,

$d(O\;,\ (AB))=OI\$ et

$\ d(O\;,\ (AC))=OK$

Par suite,

$OI=OK$

Ainsi,

$OI=OJ\$ et

$\ OI=OK$

Ce qui donne alors,

$OI=OJ=OK$

b) En déduisons que

$(b_{3})$ bissectrice de

$\widehat{C}$ passe par

$O.$

On a :

$OI=OJ=OK$

Alors,

$OJ=OK$

Ce qui signifie :

$d(O\;,\ (BC))=d(O\;,\ (AC))$

Donc, le point

$O$ est équidistant des supports des deux côtés de l'angle

$\widehat{C}.$

Par conséquent,

$O$ appartient à la bissectrice

$(b_{3})$ de l'angle

$\widehat{C}.$

D'où,

$(b_{3})$ passe par

$O.$

c) Énonçons la propriété que nous venons de démontrer pour les bissectrices.

Propriété : Dans un triangle, les trois bissectrices sont concourantes (se coupent en un même point).

d) Le point

$O$ représente le centre du cercle inscrit dans le triangle

$ABC$

Exercice 2

Construisons un triangle

$MNP$ tel que :

$MN=6\;cm\;;\ NP=5\;cm\ \text{ et }\ MP=7\;cm$

1) La bissectrice de l'angle

$\widehat{M}$ coupe

$[NP]$ en

$E.$

2) La bissectrice de l'angle

$\widehat{N}$ coupe

$(ME)$ en

$I.$

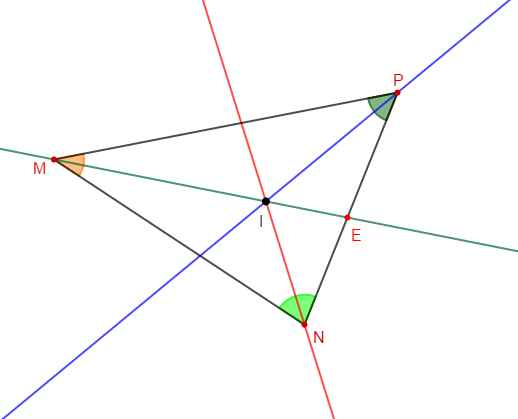
3) Démontrons que

$(IP)$ est la bissectrice de l'angle

$\widehat{MPN}.$

Comme la bissectrice de l'angle

$\widehat{M}$ coupe le segment

$[NP]$ en

$E$ alors, la droite

$(ME)$ représente la bissectrice de l'angle

$\widehat{M}.$

De plus, la bissectrice de l'angle

$\widehat{N}$ coupe

$(ME)$ en

$I.$

Cela signifie que la bissectrice de l'angle

$\widehat{M}$ et bissectrice de l'angle

$\widehat{N}$ se rencontrent en

$I.$

Or, dans un triangle, les trois bissectrices se coupent en un même point.

Par conséquent, la troisième bissectrice, celle de l'angle

$\widehat{P}$ , passe aussi par le point

$I.$

Ce qui montre que

$(IP)$ est la bissectrice de l'angle

$\widehat{MPN}.$

Exercice 3

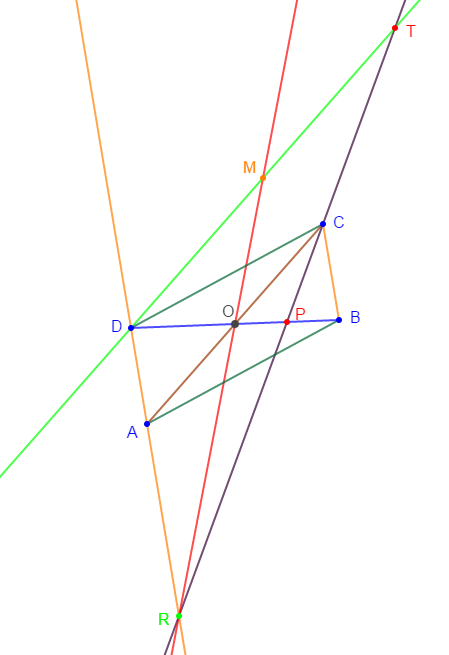
$ABCD$ est un parallélogramme de centre

$O\;,\ P$ est le milieu de

$[OB].$

Les droites

$(CP)\$ et

$\ (DA)$ se coupent en

$R.$

$T$ est le symétrique de

$R$ par rapport à

$P$

Les droites

$(RO)\$ et

$\ (DT)$ se coupent en

$M.$

1) Faisons une figure complète.

2) Montrons que

$(DP)$ est une médiane de

$RDT.$

Comme

$T$ est le symétrique de

$R$ par rapport à

$P$ alors,

$P$ est le milieu de

$[RT]$

Or, la droite

$(DP)$ passe par le sommet

$D$ du triangle

$RDT$ et par milieu

$P$ du côté opposé à ce sommet.

Donc,

$(DP)$ est une médiane de

$RDT.$

3) Montrons que

$DO=\dfrac{2}{3}DP$

On a :

$DO+OP=DP$

Or,

$P$ est milieu de

$[OB]$ ce qui signifie que

$OP=\dfrac{1}{2}OB$

Donc, en remplaçant

$OP$ par

$\dfrac{1}{2}OB$ , on obtient :

$DO+OP=DO+\dfrac{1}{2}OB=DP$

Par ailleurs,

$O$ est le centre du parallélogramme

$ABCD$ donc,

$O$ est le milieu des deux diagonales de

$ABCD.$

Ainsi,

$O$ est milieu de

$DB$

Alors,

$OB=DO$

Donc, en remplaçant

$OB=DO$ , on obtient :

$DO+\dfrac{1}{2}OB=DO+\dfrac{1}{2}DO=DP$

Par suite,

$\begin{array}{rcl} DO+\dfrac{1}{2}DO=DP&\Rightarrow&\dfrac{2DO}{2}+\dfrac{DO}{2}=DP\\\\&\Rightarrow&\dfrac{2DO+DO}{2}=DP\\\\&\Rightarrow&\dfrac{3DO}{2}=DP\\\\&\Rightarrow&3DO=2DP\\\\&\Rightarrow&DO=\dfrac{2}{3}DP\end{array}$

D'où,

$\boxed{DO=\dfrac{2}{3}DP}$

$O$ est le centre de gravité du triangle

$RDT.$

En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.

Or, le point

$O$ situé sur la médiane issue de

$D$ vérifie :

$DO=\dfrac{2}{3}DP$

Par conséquent,

$O$ est le centre de gravité du triangle

$RDT.$

5) Démontrons que

$M$ est milieu du segment

$[DT].$

La droite

$(RO)$ passe par

$R$ et par

$O$ centre de gravité du triangle

$RDK$ donc,

$(RO)$ est une médiane.

On sait que : dans un triangle, une médiane est une droite passant un sommet et par le milieu du côté opposé à ce sommet.

Or, le côté opposé au sommet

$R$ est le segment

$[DT]$ et que

$(RO)$ coupe

$(DT)$ en

$M.$

Par conséquent,

$M$ est milieu de

$[DT].$

Exercice 4

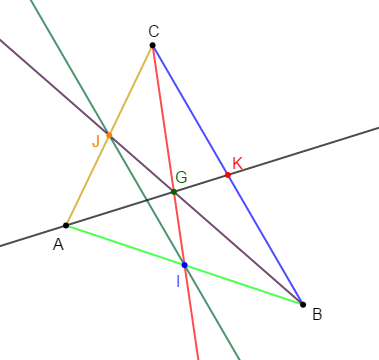
1) Construisons un triangle

$ABC$ tel que :

$AB=5\;cm\;,\ AC=4\;cm\$ et

$\ BC=6\;cm.$

$I\$ et

$\ J$ sont les milieux respectifs de

$[AB]\$ et

$\ [AC].$

2) Montrons que les droites

$(IJ)\$ et

$\ (BC)$ sont parallèles puis calculons

$IJ.$

Considérons le triangle

$ABC$ , on remarque alors que la droite

$(IJ)$ passe par les points

$I\$ et

$\ J$ milieux respectifs des côtés

$[AB]\$ et

$\ [AC].$

Donc, d'après le théorème de la droite des milieux les droites

$(IJ)\$ et

$\ (BC)$ sont parallèles.

Par ailleurs, d'après une conséquence du théorème de la droite des milieux, on a :

$IJ=\dfrac{BC}{2}$

Par suite, en remplaçant

$BC$ par sa valeur, on obtient :

$IJ=\dfrac{6}{2}=3$

D'où,

$\boxed{IJ=3\;cm}$

3) Les demi-droites

$[BJ)\$ et

$\ [CI)$ se coupent en

$G.$

a) Les demi-droites

$[BJ)\$ et

$\ [CI)$ sont des médianes du triangle

$ABC$

b) Le point

$G$ est le centre de gravité du triangle

$ABC$

4) Soit

$K$ le milieu du segment

$[BC].$ Montrons que les points

$A\;,\ G\$ et

$\ K$ sont alignés.

En effet, la droite

$(AK)$ passe par le sommet

$A$ et par

$K$ ; milieu du côté opposé à ce sommet.

Par conséquent,

$(AK)$ est une médiane du triangle

$ABC.$

Or,

$G$ est le centre de gravité du triangle

$ABC$ donc, la droite

$(AK)$ passe par

$G.$

Par suite,

$A\;,\ G\$ et

$\ K$ appartiennent à la même droite

$(AK).$

D'où, les points

$A\;,\ G\$ et

$\ K$ sont alignés.

5) On donne

$AK=3\;cm$ . Calculons

$AG\$ et

$\ GK.$

En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.

Ce qui signifie que :

$AG=\dfrac{2}{3}AK$

Donc, en remplaçant

$AK$ par sa valeur, on obtient :

$AG=\dfrac{2\times 3}{3}=2$

Ainsi,

$\boxed{AK=2\;cm}$

Par ailleurs, on a :

$G\in[AK]$ alors,

$AG+GK=AK$

Par suite,

$\begin{array}{rcl} GK&=&AK-AG\\\\&=&3-2\\\\&=&1\end{array}$

D'où,

$\boxed{GK=1\;cm}$

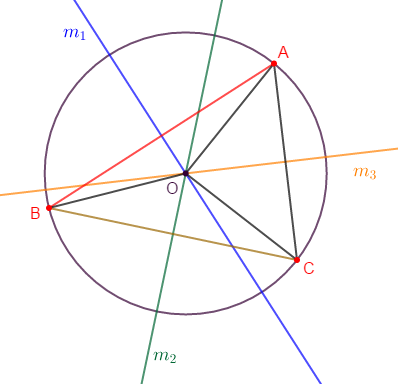
Exercice 5

1) Construisons un triangle

$ABC$ quelconque.

2) a) Construisons la droite

$(m_{1})$ médiatrice de

$[AB].$

b) Construisons la droite

$(m_{2})$ médiatrice de

$[BC].$

2) a) Les droites

$(m_{1})\$ et

$\ (m_{2})$ se coupent en

$O.$

3) a) Démontrons que :

$OA=OB=OC.$

On a :

$(m_{1})$ médiatrice de

$[AB]\$ et

$\ O\in(m_{1})$

En effet, on sait que : si un point appartient à la médiatrice d'un segment alors, ce point est à égale distance des extrémités de ce segment.

Or,

$O\in(m_{1})$ médiatrice du segment

$[AB]$ donc,

$O$ est équidistant des extrémités

$A\$ et

$\ B$ de ce segment.

Ce qui se traduit par :

$OA=OB$

De la même manière, comme

$O\in(m_{2})$ médiatrice du segment

$[BC]$ alors,

$O$ est à égale distance des extrémités

$B\$ et

$\ C$ de ce segment.

Ce qui peut s'écrire :

$OB=OC$

Ainsi, on a :

$OA=OB\$ et

$\ OB=OC$

D'où,

$\boxed{OA=OB=OC}$

b) En déduisons que la droite

$(m_{3})$ médiatrice de

$[AC]$ passe par

$O.$

En effet, on sait que tout point situé à égale distance des extrémités d'un segment appartient à la médiatrice de ce segment.

Or, d'après le résultat de 3) a) on a :

$OC=OA$

Ce qui signifie que le point

$O$ est à égale distance des points

$A\$ et

$\ C.$

Par conséquent,

$O$ appartient à la médiatrice du segment

$[AC].$

D'où, la droite

$(m_{3})$ médiatrice de

$[AC]$ passe par

$O.$

c) Énonçons la propriété que nous venons de démontrer pour les médiatrices.

Dans un triangle, les médiatrices des côtés se coupent en un point.

d) Le point

$O$ est le centre du cercle circonscrit au triangle

$ABC$

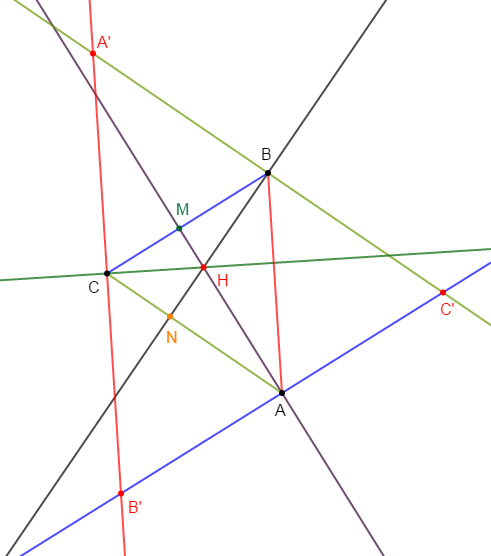
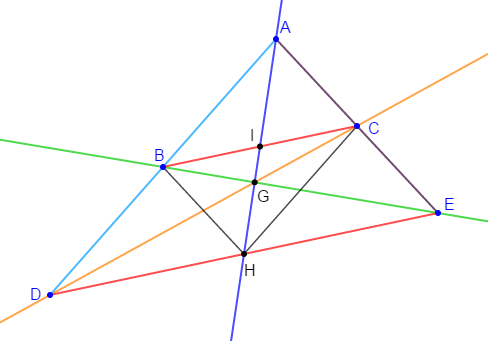
Exercice 6

1) Construisons un triangle

$ABC$ quelconque.

2) a) Construisons

$(AM)$ hauteur issue de

$A.$

b) Construisons la droite

$(BN)$ hauteur issue de

$B.$

3) Les deux droites

$(AM)\$ et

$\ (BN)$ se coupent en

$H$ , plaçons le point

$H.$

4) a) Construisons la droite

$(B'C')$ passant par

$A$ et parallèle à

$(BC).$

b) Construisons la droite

$(A'C')$ passant par

$B$ et parallèle à

$(AC).$

c) Construisons la droite

$(B'A')$ passant par

$C$ et parallèle à

$(AB).$

5) Démontrons que les quadrilatères

$ABCB'\;;\ BCAC'\$ et

$\ CABA'$ sont des parallélogrammes.

On a :

$(B'C)\parallel(AB)\$ et

$\ (BC)\parallel(B'A)$

Donc, le quadrilatère

$ABCA'$ a ses côtés parallèles

$2$ à

$2.$

Par conséquent,

$ABCA'$ est un parallélogramme.

On a :

$(BC)\parallel(AC')\$ et

$\ (AC)\parallel(BC')$

Donc, le quadrilatère

$BCAC'$ a ses côtés parallèles

$2$ à

$2.$

D'où,

$BCAC'$ est un parallélogramme.

On a :

$(A'C)\parallel(AB)\$ et

$\ (AC)\parallel(A'B)$

Donc, le quadrilatère

$CABA'$ a ses côtés parallèles

$2$ à

$2.$

Par conséquent,

$CABA'$ est un parallélogramme.

6) a) Démontrons que

$(AH)$ est la médiatrice de

$[B'C'].$

En effet, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est aussi perpendiculaire à l'autre.

Or, dans le triangle

$ABC$ , on a :

$(AH)$ hauteur issue de

$A$ donc,

$(AH)$ perpendiculaire à

$(BC).$

De plus,

$(BC)\parallel(B'C')$

Par suite,

$(AH)$ est perpendiculaire à

$(B'C').$

Par ailleurs,

$ABCB'\$ et

$\ ABCB'$ sont des parallélogrammes alors,

$BC=AC'\$ et

$\ BC=AC'.$

Or,

$B'\;,\ A\$ et

$\ C'$ alignés donc,

$A$ est milieu de

$[B'C']$

Ainsi,

$(AH)$ est perpendiculaire à

$[B'C']$ et passe par le milieu de ce segment.

Par conséquent,

$(AH)$ est la médiatrice de

$[B'C'].$

b) Démontrons que

$(BH)$ est la médiatrice de

$[A'C'].$

Dans le triangle

$ABC$ , on a :

$(BH)$ hauteur issue de

$B$ alors,

$(BH)$ est perpendiculaire à

$(AC).$

Or,

$(AC)$ est parallèle à

$(A'C').$

Donc,

$(BH)$ est perpendiculaire à

$(A'C').$

De plus, comme

$CABA'\$ et

$\ BCAC'$ sont des parallélogrammes alors, on a :

$AC=A'B\$ et

$\ AC=BC'.$

Or, les points

$A'\;,\ B\$ et

$\ C'$ sont alignés donc,

$B$ est milieu de

$[A'C']$

Ainsi,

$(BH)$ est perpendiculaire à

$[A'C']$ et passe par le milieu de ce segment.

Par conséquent,

$(BH)$ est la médiatrice de

$[A'C'].$

c) Démontrons que

$(CH)$ est la troisième médiatrice du triangle

$A'B'C'.$

On a :

$H$ appartient à la médiatrice de

$[B'C']$ alors,

$HB'=HC'$

$H$ appartient à la médiatrice de

$[A'C']$ alors,

$HA'=HC'$

Ainsi,

$HB'=HC'\$ et

$\ HA'=HC'$

Par suite,

$HB'=HA'$ ce qui signifie que

$H$ est situé à égale distance des points

$A'\$ et

$\ B'.$

Or, on sait que tout point situé à égale distance des extrémités d'un segment appartient à la médiatrice de ce segment.

Donc,

$H$ appartient à la médiatrice de

$[A'B'].$

De plus,

$C$ est milieu de

$[A'B'].$

Par conséquent,

$(CH)$ est la troisième médiatrice du triangle

$A'B'C'.$

7) a) Les médiatrices du triangle

$A'B'C'$ représentent les hauteurs du triangle

$ABC$

b) Énonçons la propriété que nous venons de démontrer pour les hauteurs du triangle.

Dans un triangle, les trois hauteurs se coupent en un point.

c) Le point

$H$ représente l'orthocentre du triangle

$ABC$

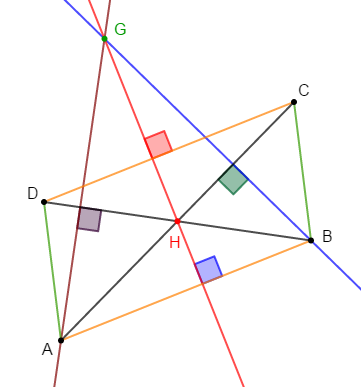
Exercice 7

Soit

$ABCD$ un parallélogramme de centre

$H.$

La perpendiculaire à

$(DB)$ passant par

$A$ et la perpendiculaire à

$(AC)$ passant par

$B$ se coupent en

$G.$

1) Faisons une figure.

2) Le point

$H$ est l'orthocentre du triangle

$AGB.$

3) Montrons que les droites

$(GH)\$ et

$\ (AB)$ sont perpendiculaires.

Comme

$H$ est l'orthocentre de

$AGB$ alors, la droite

$(GH)$ passant par le sommet

$G$ et par

$H$ est hauteur du triangle

$AGB.$

Par suite,

$(GH)$ est perpendiculaire au côté opposé au sommet

$G.$

D'où, les droites

$(GH)\$ et

$\ (AB)$ sont perpendiculaires.

4) Montrons que les droites

$(GH)\$ et

$\ (DC)$ sont perpendiculaires.

En effet, comme

$ABCD$ est un parallélogramme alors, les droites

$(AB)\$ et

$\ (DC)$ sont parallèles.

De plus, d'après le résultat de

$3)$ , les droites

$(GH)\$ et

$\ (AB)$ sont perpendiculaires.

Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est aussi perpendiculaire à l'autre.

Par conséquent, les droites

$(GH)\$ et

$\ (DC)$ sont perpendiculaires.

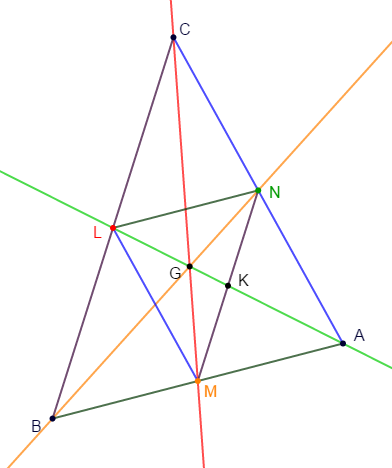
Exercice 8

Soit

$ABC$ un triangle tel que :

$AB=6\;cm\;;\ AC=7\;cm\$ et

$\ BC=8\;cm.$

Les points

$L\;,\ M\$ et

$\ N$ sont les milieux respectifs des côtés

$[BC]\;,\ [AB]\$ et

$\ [AC]$ du triangle.

$G$ est le centre de gravité.

1) Faisons une figure complète.

2) Démontrons que

$MLNA$ est un parallélogramme. Soit

$K$ sont centre.

Considérons le triangle

$ABC.$

On a :

$M\$ et

$\ L$ milieux respectifs des côtés

$[AB]\$ et

$\ [BC].$

Donc, d'après le théorème de la droite des milieux la droite

$(ML)$ passant par

$M\$ et

$\ L$ est parallèle à la droite

$(AC).$

Par suite,

$(ML)$ est parallèle à

$(AN)$

De la même manière, on a :

$N\$ et

$\ L$ milieux respectifs des côtés

$[AC]\$ et

$\ [BC].$

Alors, d'après le théorème de la droite des milieux la droite

$(NL)$ passant par

$N\$ et

$\ L$ est parallèle à la droite

$(AC).$

Donc,

$(NL)$ est parallèle à

$(AM)$

Ainsi, on a :

$(ML)\parallel(AN)\$ et

$\ (NL)\parallel(AM)$

Donc, le quadrilatère

$MLNA$ a ses côtés parallèles

$2$ à

$2.$

Par conséquent, c'est un parallélogramme.

En déduisons que :

$AK=\dfrac{1}{2}AL$ puis

$KG=\dfrac{1}{6}AL$

Comme

$K$ est le centre du parallélogramme

$MLNA$ alors,

$K$ est milieu de

$[AL].$

D'où,

$\boxed{AL=\dfrac{1}{2}AL}$

Par ailleurs,

$G$ étant le centre de gravité du triangle

$ABC$ donc,

$AG=\dfrac{2}{3}AL$

Comme

$K\in[AG]$ alors, on a :

$KG+AK=AG$

Donc,

$KG=AG-AK$

Par suite, en remplaçant

$AG\$ et

$\ AK$ par leur expression, on obtient :

$\begin{array}{rcl} KG&=&AG-AK\\\\&=&\dfrac{2}{3}AL-\dfrac{1}{2}AL\\\\&=&\dfrac{4}{6}AL-\dfrac{3}{6}AL\\\\&=&\dfrac{1}{6}AL\end{array}$

D'où,

$\boxed{KG=\dfrac{1}{6}AL}$

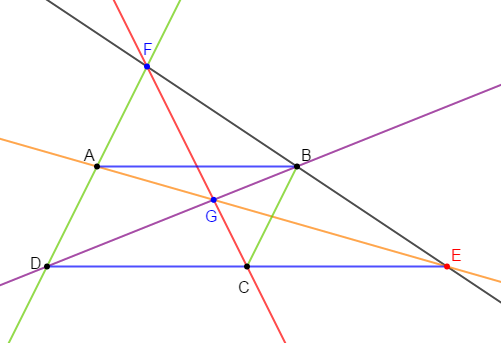
Exercice 9

Soit

$ABCD$ un parallélogramme et

$E$ le symétrique de

$D$ par rapport à

$C.$ Les droites

$(AD)\$ et

$\ (BE)$ se coupent en

$F.$

1) Montrons que

$B$ est le milieu du segment

$[EF].$

Considérons le triangle

$DEF.$

On a :

$E$ le symétrique de

$D$ par rapport à

$C$ donc,

$C$ est milieu de

$[DE].$

Comme

$ABCD$ est un parallélogramme alors,

$(BC)$ est parallèle à

$(AD).$

C'est à dire

$(BC)\$ et

$\ (DF)$ sont parallèles.

Ainsi, d'après le théorème de la droite des milieux, la droite

$(BC)$ passant par le milieu de

$[DE]$ et parallèle à

$(DF)$ coupe

$[FE]$ en son milieu.

Par conséquent,

$B$ est le milieu du segment

$[EF].$

2) Montrons que

$A$ est le milieu du segment

$[DF].$

Comme

$ABCD$ est un parallélogramme alors,

$(AB)\$ et

$(DC)$ sont parallèles.

C'est à dire

$(AB)$ parallèle à

$(DE).$

En considérant le triangle

$DEF$ , on remarque que la droite

$(AB)$ passant par

$B$ milieu de

$[EF]$ et parallèle à

$(DE)$ , coupe

$[DF]$ en

$A.$

Donc, en appliquant le théorème de la droite des milieux dans ce triangle, on obtient :

$A$ milieu de

$[DF].$

3) Les droites

$(FC)\$ et

$\ (DB)$ se coupent en

$G.$ Démontrons que les points

$A\;,\ G\$ et

$\ E$ sont alignés.

En effet,

$(FC)\$ et

$\ (DB)$ sont deux médianes du triangle

$DEF.$

Donc,

$G$ est le centre de gravité de ce triangle.

Comme la droite

$(AE)$ passe par le sommet

$E$ et par le milieu

$A$ du segment

$[DF]$ alors,

$(AE)$ est la troisième médiane du triangle

$DEF.$

Par conséquent, elle passe par le point

$G.$

Ainsi, les points

$A\;,\ G\$ et

$\ E$ appartiennent à une même droite.

Ce qui montre que ces points sont alignés.

Exercice 10

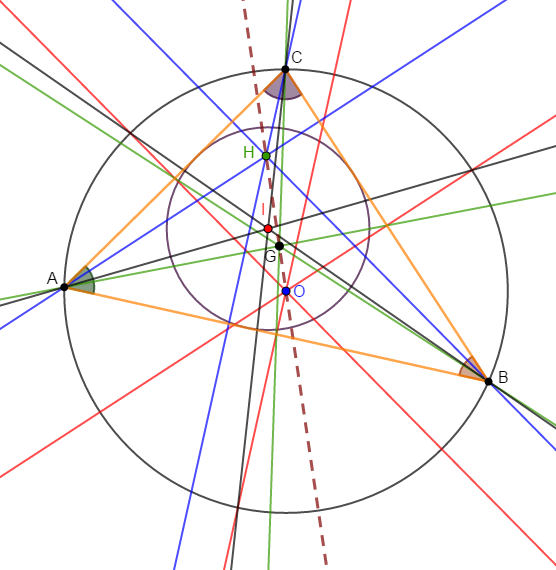
1) Construisons un triangle

$ABC$ tel que

$AB=14\;cm\;,\ AC=10\;cm\$ et

$\ BC=12\;cm.$

2) Construisons ses médiatrices en rouge, ses médianes en vert, ses hauteurs en bleu et ses bissectrices en noir.

3) Plaçons le point

$G$ centre de gravité du triangle, le point

$O$ centre du cercle circonscrit, le point

$I$ centre du cercle inscrit et le point

$H$ orthocentre du triangle.

4) Pour ce triangle

$ABC$ , construisons les cercles circonscrit et inscrit.

5) Traçons la droite qui passe par

$O\$ et

$\ G.$

Nous constatons que cette droite passe par

$H.$

Exercice 11

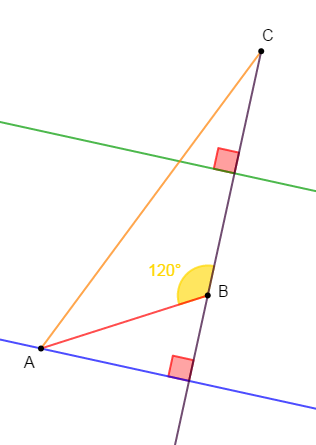
Construis le triangle

$ABC$ tel que :

$AB=3.5\;cm\;,\ \widehat{ABC}=120^{\circ}\$ et

$\ BC=5\;cm.$

1) Traçons en bleu la hauteur issue de

$A$ et en vert la médiatrice du segment

$[BC].$

2) Démontrons que ces deux droites sont parallèles.

En effet, la hauteur issue de

$A$ est la droite passant par

$A$ et perpendiculaire au côté opposé au sommet

$A.$

Donc, la hauteur est perpendiculaire à la droite

$(BC).$

Par ailleurs, la médiatrice du segment

$[BC]$ est la droite perpendiculaire à la droite

$(BC)$ et passant par le milieu du segment

$[BC].$

Or, on sait que : si deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.

D'où, la hauteur issue de

$A$ et la médiatrice de

$[BC]$ sont parallèles.

Exercice 12

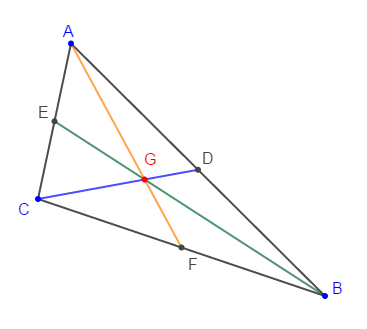
$ABC$ est un triangle de centre de gravité

$G.$

$E\;,\ D\$ et

$\ F$ sont les milieux respectifs de

$[AC]\;,\ [AB]\$ et

$\ [BC].$

On donne :

$AE=2\;cm\;,\ AG=3\;cm\;,\ GD=1\;cm\$ et

$\ BE=6\;cm.$

Calculons

$AC\;,\ GF\;,\ GC\;,\ BG\$ et

$\ GE.$

$-\$ Calcul de

$AC$

Comme

$E$ est milieu de

$[AC]$ alors,

$AC=2AE.$

Donc, en remplaçant

$AE$ par sa valeur, on obtient :

$AC=2\times 2=4$

D'où,

$\boxed{AC=4\;cm}$

$-\$ Calcul de

$GF$

En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.

Donc,

$AG=\dfrac{2AF}{3}$

Par suite,

Comme

$AG+GF=AF$ alors,

$GF=AF-AG$

En remplaçant

$AG$ par son expression, on obtient :

$\begin{array}{rcl} GF&=&AF-AG\\\\&=&AF-\dfrac{2AF}{3}\\\\&=&\dfrac{3AF}{3}-\dfrac{2AF}{3}\\\\&=&\dfrac{AF}{3}\end{array}$

Donc,

$GF=\dfrac{AF}{3}$

Ainsi, on a :

$\left\lbrace\begin{array}{rcl} AG&=&2\times\dfrac{AF}{3}\\\\GF&=&\dfrac{AF}{3}\end{array}\right.\ \Rightarrow\ AG=2GF$

Par suite,

$GF=\dfrac{AG}{2}=\dfrac{3}{2}=1.5$

D'où,

$\boxed{GF=1.5\;cm}$

$-\$ Calcul de

$GC$

En procédant de la même manière que dans le calcul précédent, on obtient :

$\left\lbrace\begin{array}{rcl} GC&=&2\times\dfrac{CD}{3}\\\\GD&=&\dfrac{CD}{3}\end{array}\right.\ \Rightarrow\ GC=2GD$

Par suite,

$GC=2\times 1=2$

Ainsi,

$\boxed{GC=2\;cm}$

$-\$ Calcul de

$BG$

Comme le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet alors, on a :

$GB=\dfrac{2BE}{3}$

Ce qui donne :

$GB=\dfrac{2\times 6}{3}=\dfrac{12}{3}=4$

Ainsi,

$\boxed{GB=4\;cm}$

$-\$ Calcul de

$GE$

On a :

$GE+GB=BE$ donc,

$GE=BE-GB$

Ainsi,

$GE=6-4=2$

D'où,

$\boxed{GE=2\;cm}$

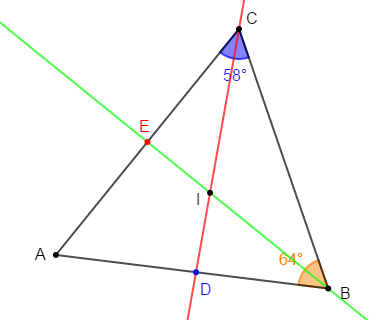
Exercice 13

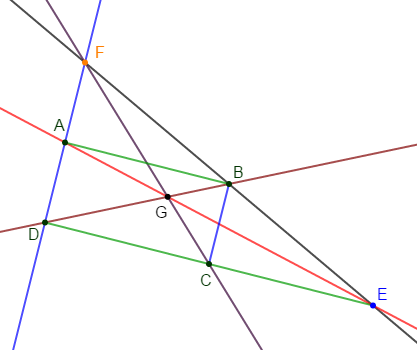
Sur la figure ci-dessous,

$\widehat{ABC}=64^{\circ}\$ et

$\ \widehat{ACB}=58^{\circ}.$

$(BE)$ est la bissectrice de l'angle

$\widehat{B}\$ et

$\ (CD)$ est la bissectrice de l'angle

$\widehat{C}.$

Les deux bissectrices se coupent en

$I.$

Calculons la mesure des angles

$\widehat{ACD}\;,\ \widehat{ADC}\;,\ \widehat{BIC}\;,\ \widehat{BAC}.$

$-\$ Calcul de la mesure de l'angle

$\widehat{ACD}$

Comme

$(CD)$ est la bissectrice de l'angle

$\widehat{C}$ alors,

$(CD)$ partage cet angle en deux angles de même mesure :

$\widehat{ACD}\$ et

$\ \widehat{DCB}$

Ainsi,

$\widehat{ACD}=\widehat{DCB}=\dfrac{\widehat{ACB}}{2}$

Par suite,

$\begin{array}{rcl}\widehat{ACD}&=&\dfrac{\widehat{ACB}}{2}\\\\&=&\dfrac{58^{\circ}}{2}\\\\&=&29^{\circ}\end{array}$

D'où,

$\boxed{\widehat{ACD}=29^{\circ}}$

$-\$ Calcul de la mesure de l'angle

$\widehat{BAC}.$

On sait que dans un triangle, la somme des angles est égale à

$180^{\circ}.$

Donc, dans le triangle

$ABC$ , on a :

$\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^{\circ}$

Par suite,

$\widehat{BAC}=180^{\circ}-\widehat{ACB}-\widehat{ABC}$

Ainsi,

$\begin{array}{rcl}\widehat{BAC}&=&180^{\circ}-58^{\circ}-64^{\circ}\\\\&=&58^{\circ}\end{array}$

D'où,

$\boxed{\widehat{BAC}=58^{\circ}}$

$-\$ Calcul de la mesure de l'angle

$\widehat{ADC}$

Comme la somme des angles d'un triangle est égale à

$180^{\circ}$ alors, en considérant le triangle

$ADC$ , on a :

$\widehat{ADC}+\widehat{ACD}+\widehat{DAC}=180^{\circ}$

Ce qui donne :

$\widehat{ADC}=180^{\circ}-\widehat{ACD}-\widehat{DAC}$

Par suite,

$\begin{array}{rcl}\widehat{ADC}&=&180^{\circ}-29^{\circ}-58^{\circ}\\\\&=&93^{\circ}\end{array}$

Ainsi,

$\boxed{\widehat{ADC}=93^{\circ}}$

$-\$ Calcul de la mesure de l'angle

$\widehat{BIC}$

En considérant le triangle

$BIC$ , on a :

$\widehat{BIC}+\widehat{ICB}+\widehat{CBI}=180^{\circ}$

Comme

$(BE)$ est la bissectrice de l'angle

$\widehat{B}$ alors,

$(BE)$ partage cet angle en deux angles de même mesure.

Ainsi,

$\widehat{CBI}=\dfrac{\widehat{ABC}}{2}=\dfrac{64^{\circ}}{2}=32^{\circ}$

Par ailleurs, on a :

$\widehat{ICB}=\widehat{DCB}\$ et

$\ \widehat{DCB}=\widehat{ACD}=29^{\circ}$

Donc,

$\widehat{ICB}=29^{\circ}$

Alors, les angles du triangle

$BIC$ vérifient :

$\widehat{BIC}+29^{\circ}+32^{\circ}=180^{\circ}$

Par suite

$\begin{array}{rcl}\widehat{BIC}&=&180^{\circ}-29^{\circ}-32^{\circ}\\\\&=&119^{\circ}\end{array}$

D'où,

$\boxed{\widehat{BIC}=119^{\circ}}$

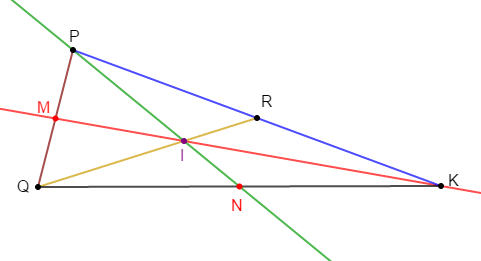
Exercice 14

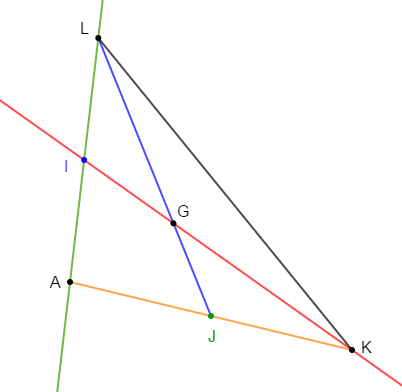
On donne un segment

$[AK].$

Soit

$J$ son milieu.

Plaçons un point

$L$ n'appartenant pas à

$(AK)$ tel que

$JL=6\;cm.$

Plaçons sur

$[JL]$ le point

$G$ tel que

$LG=4\;cm.$

$(KG)$ coupe

$(AL)$ en

$I.$

Démontons que

$I$ est le milieu de

$[AL].$

Considérons le triangle

$AKL.$

Comme

$J$ est milieu de

$[AK]$ alors,

$[LJ)$ est la médiane issue de

$L.$

Par ailleurs, en calculant le rapport

$\dfrac{LG}{JL}$ , on trouve :

$\dfrac{LG}{JL}=\dfrac{4}{6}=\dfrac{2}{3}$

Donc,

$\dfrac{LG}{JL}=\dfrac{2}{3}$

Par suite,

$LG=\dfrac{2}{3}JL$

Ainsi, le point

$G$ est situé au deux tiers de

$[LJ]$ , à partir du sommet

$L.$

Ce qui signifie que

$G$ est le centre de gravité du triangle

$AKL.$

Par conséquent, la droite

$(KG)$ , passant par le sommet

$K$ et par

$G$ , est aussi une médiane de ce triangle.

De plus,

$(KG)$ coupe

$[AL]$ en

$I.$

Or, on sait que : dans un triangle, une médiane issue d'un sommet, coupe le côté opposé à ce sommet en son milieu.

D'où,

$I$ est le milieu de

$[AL].$

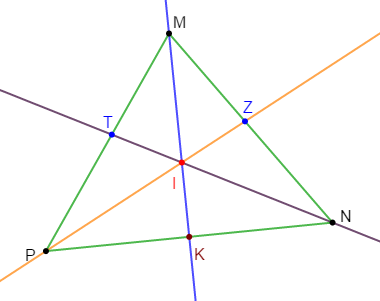
Exercice 15

$MNP$ est un triangle isocèle en

$M\;,\ K$ est le milieu de

$[NP].$

Les bissectrices

$(PZ)\$ et

$\ (NT)$ des angles

$\widehat{MPN}\$ et

$\ \widehat{MNP}$ se coupent en

$I.$

Démontrons que

$(MK)$ passe par

$I.$

En effet, la droite

$(MK)$ passant le sommet

$M$ , coupe

$[PN]$ par le milieu

$K.$ Donc,

$(MK)$ est aussi médiane du triangle

$MNP.$

Comme le triangle

$MNP$ est isocèle en

$M$ alors, la médiane

$(MK)$ issue de

$M$ est aussi bissectrice de l'angle

$\widehat{PMN}.$

De plus, on sait que : dans un triangle, les trois bissectrices se coupent en un point.

Or, les deux bissectrices

$(PZ)\$ et

$\ (NT)$ se coupent en

$I.$

Par conséquent, la troisièmes bissectrice

$(MK)$ passe alors par

$I.$

Exercice 16

$KELI$ est un parallélogramme de centre

$O.$

1) Construisons le point

$M$ centre de gravité du triangle

$KEI$ et le point

$N$ centre de gravité du triangle

$ILE.$

2) Démontre que les points

$K\;,\ M\;,\ O\;,\ N\$ et

$\ L$ sont alignés.

En effet,

$KELI$ étant un parallélogramme de centre

$O$ alors, ses diagonales

$[IE]\$ et

$\ [KL]$ ont même milieu

$O.$

Dans le triangle

$KEI$ , on a :

$(KL)$ passe par le sommet

$K$ et par le milieu

$O$ du côté opposé à ce sommet donc,

$(KL)$ est une médiane de ce triangle.

Donc,

$(KL)$ passe par le centre de gravité

$M$ du triangle

$KEI.$

Par suite,

$K\;,\ M\;,\ O$ appartiennent à la même droite

$(KL).$

De la même manière, en considérant le triangle

$ILE$ , on a :

$(KL)$ passe par

$L\$ et

$\ O$ donc, la droite

$(KL)$ est une médiane de ce triangle.

Elle passe alors par le centre de gravité

$N$ du triangle

$ILE.$

Par suite,

$L\;,\ N\;,\ O$ appartiennent à la même droite (

$KL).$

Ainsi,

$K\;,\ M\;,\ O\;,\ N\;,\ L$ appartiennent tous à la même droite

$(KL).$

Par conséquent, ces points sont alignés.

3) Démontrons que

$KM=MN=NL.$

En effet, on sait que : le centre de gravité d'un triangle est situé au deux tiers de chaque médiane, à partir du sommet.

Donc :

dans le triangle

$KEI$ , on a :

$KM=\dfrac{2}{3}KO$

dans le triangle

$ILE$ , on a :

$NL=\dfrac{2}{3}LO$

Or, le point

$O$ est milieu de

$[KL]$ donc,

$KO=LO=\dfrac{KL}{2}$

Ainsi, en remplaçant

$KO\$ et

$\ LO$ par

$\dfrac{KL}{2}$ , on obtient :

$\begin{array}{rcl} KM&=&\dfrac{2}{3}KO\\\\&=&\dfrac{2}{3}\times\dfrac{KL}{2}\\\\&=&\dfrac{KL}{3}\end{array}$

Donc,

$\boxed{KM=\dfrac{KL}{3}}$

$\begin{array}{rcl} NL&=&\dfrac{2}{3}LO\\\\&=&\dfrac{2}{3}\times\dfrac{KL}{2}\\\\&=&\dfrac{KL}{3}\end{array}$

Ainsi,

$\boxed{NL=\dfrac{KL}{3}}$

Par ailleurs, on a :

$KM+MN+NL=KL$

Ce qui donne alors,

$MN=KL-KM-NL$

Donc, en remplaçant

$KM\$ et

$\ NL$ par

$\dfrac{KL}{3}$ , on obtient :

$\begin{array}{rcl} MN&=&KL-KM-NL\\\\&=&KL-\dfrac{KL}{3}-\dfrac{KL}{3}\\\\&=&KL-\dfrac{2KL}{3}\\\\&=&\dfrac{3KL}{3}-\dfrac{2KL}{3}\\\\&=&\dfrac{KL}{3}\end{array}$

Donc,

$\boxed{MN=\dfrac{KL}{3}}$

Ainsi, on a :

$\left\lbrace\begin{array}{rcl} KM=\dfrac{KL}{3}\\\\MN=\dfrac{KL}{3}\\\\MN=\dfrac{KL}{3}\end{array}\right.$

Par conséquent,

$\boxed{KM=MN=NL}$

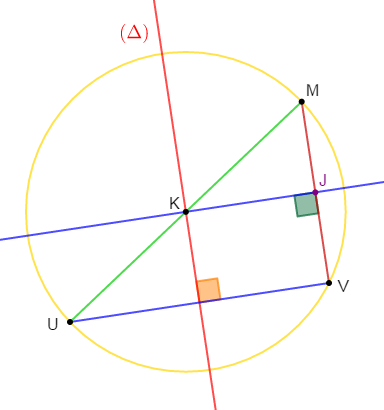
Exercice 17

1) Construisons un segment

$[UV]$ et sa médiatrice

$(\Delta).$

Marquons un point

$K$ sur cette médiatrice,

$K$ n'appartient pas à

$[UV]$ et le point

$M$ symétrique de

$U$ par rapport à

$K.$

2) Démontrons que

$K$ est le centre du cercle circonscrit au triangle

$MUV.$

On considère le triangle

$MUV.$

On a :

$(\Delta)$ médiatrice de

$[UV]$ alors,

$(\Delta)$ est perpendiculaire à

$(UV)$ et passe par le milieu de

$[UV].$

Par ailleurs,

$M$ symétrique de

$U$ par rapport à

$K$ donc,

$K$ est milieu de

$[MU].$

Ainsi, d'après le théorème de la droite des milieux,

$(\Delta)$ est parallèle à

$(MV).$

Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.

Donc,

$(UV)$ est perpendiculaire à

$(MV).$

D'où,

$MUV$ est un tringle rectangle en

$V.$

Par conséquent, le centre du cercle circonscrit est le milieu

$K$ de l'hypoténuse

$[MU].$

3) La parallèle à

$(UV)$ passant par

$K$ coupe

$(MV)$ en

$J.$

Démontrons que

$(KJ)$ est la médiatrice du segment

$[MV].$

En effet, considérons le triangle

$MUV.$

Comme

$K$ est milieu de

$[MU]$ alors, d'après la réciproque du théorème de la droite des milieux, la parallèle à

$(UV)$ passant par

$K$ coupe

$[MV]$ en son milieu.

Donc,

$J$ est milieu de

$[MV]$

Par ailleurs, comme

$(KJ)$ est parallèle à

$(UV)\$ et

$\ (MV)$ est perpendiculaire à

$(UV)$ alors,

$(KJ)$ est perpendiculaire à

$(MV).$

Ainsi, on a :

$(KJ)$ est perpendiculaire à

$(MV)$ et passe par le milieu de

$[MV].$

Par conséquent,

$(KJ)$ est la médiatrice du segment

$[MV].$

Exercice 18

Traçons un triangle

$ABC.$

On appelle

$D$ le symétrique de

$A$ par rapport à

$B$ et

$E$ le symétrique de

$A$ par rapport à

$C.$

1) Démontrons que les droites

$(BC)$ et

$(DE)$ sont parallèles.

Considérons le triangle

$ADE.$

On a :

$D$ symétrique de

$A$ par rapport à

$B$ alors,

$B$ est milieu de

$[AD]$

$E$ symétrique de

$A$ par rapport à

$C$ donc,

$C$ est milieu de

$[AE]$

Alors, d'après le théorème de la droite des milieux, la droite

$(BC)$ passant par

$B\$ et

$\ C$ milieux respectifs des segments

$[AD]\$ et

$\ [AE]$ est parallèle à la droite

$(DE).$

2) On appelle

$I$ le milieu du segment

$[BC].$

La droite

$(AI)$ coupe

$(DE)$ en

$H.$

Démontrons que

$I$ est le milieu du segment

$[AH].$

Considérons le triangle

$ADH.$

On a : la droite

$(BI)$ passant par

$B$ milieu de

$[AD]$ est parallèle à

$(DH).$

Donc, d'après la réciproque du théorème de la droite des milieux, la droite

$(BI)$ coupe le segment

$[AH]$ en son milieu.

Or,

$(BI)\$ et

$\ [AH]$ se coupent en

$I.$

Par conséquent,

$I$ est le milieu du segment

$[AH].$

3) Démontrons que les droites

$(DC)\;,\ (AH)\$ et

$\ (BE)$ sont concourantes.

En effet, comme

$[BC]\$ et

$\ [AH]$ ont même milieu

$I$ alors,

$ABHC$ est un parallélogramme.

Par suite,

$(BH)$ est parallèle à

$(AC).$

Or,

$B$ est milieu de

$[AD].$

Donc, en appliquant la réciproque du théorème de la droite des milieux dans le triangle

$ADE$ , on a :

$(BH)$ coupe

$[DE]$ en son milieu.

Ainsi,

$H$ est milieu de

$[DE].$

D'où,

$(AH)$ est une médiane du triangle

$ADE.$

Par ailleurs,

$(DC)\$ et

$\ (AH)$ sont aussi des médianes de ce même triangle.

Or, on sait que : dans un triangle, les médianes se coupent en un point.

Par conséquent, les droites

$(DC)\;,\ (AH)\$ et

$\ (BE)$ sont concourantes.

Exercice 19

Soit un parallélogramme

$ABCD.$

Le point

$E$ est le symétrique de

$D$ par rapport à

$C.$

Les droites

$(AD)\$ et

$\ (BE)$ se coupent en

$F.$

1) Montrons que

$B$ est le milieu de

$[EF].$

Considérons le triangle

$DEF.$

Comme

$E$ est le symétrique de

$D$ par rapport à

$C$ alors,

$C$ est milieu de

$[DE].$

Par ailleurs,

$ABCD$ étant un parallélogramme alors,

$(BC)$ est parallèle à

$(AD).$

Ainsi, dans le triangle

$DEF$ , la droite

$(BC)$ parallèle à

$(DF)$ et passant par

$C$ milieu de

$[DF]$ , coupe

$[EF]$ en

$B.$

Donc, d'après la réciproque du théorème de la droite des milieux,

$B$ est le milieu de

$[EF].$

2) Montrons que

$A$ est le milieu de

$[DF].$

En effet, comme

$ABCD$ est un parallélogramme alors,

$(AB)$ est parallèle à

$(DC).$

Donc, en considérant le triangle

$DEF$ , on a : la droite

$(AB)$ passant par

$B$ milieu de

$[EF]$ et parallèle à la droite

$(DE)$ , coupe

$[DF]$ en

$A.$

Ainsi, d'après la réciproque du théorème de la droite des milieux,

$A$ est le milieu de

$[DF].$

3) Les droites

$(DB)\$ et

$\ (FC)$ se coupent en

$G.$

Démontrons que les points

$E\;,\ G\$ et

$\ A$ sont alignés.

On a :

$(DB)\$ et

$\ (FC)$ sont deux médianes du triangle

$DEF$ qui se coupent en

$G.$

$G$ est alors le centre de gravité du triangle

$DEF.$

Comme

$(AE)$ passe par le sommet

$E$ et par le milieu

$A$ du côté opposé à ce sommet alors,

$(AE)$ est la troisième médiane du triangle

$DEF.$

Ce qui signifie que,

$(AE)$ passe aussi par

$G.$

Par conséquent, les points

$E\;,\ G\$ et

$\ A$ sont alignés.

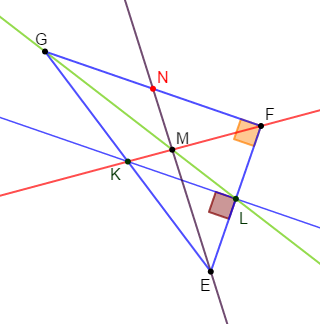
Exercice 20

1) Construisons un triangle

$EFG$ rectangle en

$F.$

Plaçons

$K$ le milieu du segment

$[EG].$

Traçons la droite passant par

$K$ et perpendiculaire à

$(EF).$

Elle coupe

$[EF]$ en

$L.$

2) Démontrons que

$L$ est le milieu du segment

$[EF].$

Dans le triangle

$EFG$ , on a :

$K$ milieu de

$[GF].$

De pus, on sait que : si deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.

Or,

$(EF)$ perpendiculaire à

$(KL)\$ et

$\ (EF)$ perpendiculaire à

$(GF).$

Par conséquent,

$(KL)\$ et

$\ (GF)$ sont parallèles.

Donc, en appliquant la réciproque du théorème de la droite des milieux,

$L$ est le milieu de

$[EF].$

3) Les droites

$(FK)\$ et

$\ (GL)$ se coupent en

$M.$

Les droites

$(FK)\$ et

$\ (GL)$ représentent des médianes du triangle

$EFG$

En effet, ces droites passent par un sommet et par le milieu du côté opposé au sommet.

Par conséquent, ce sont des médianes du triangle

$EFG.$

Déduisons-en que la droite

$(EM)$ coupe le segment

$[FG]$ en son milieu.

En effet, on a : les deux médianes

$(FK)\$ et

$\ (GL)$ se coupent en

$M$ donc,

$M$ est le centre de gravité du triangle

$EFG.$

Comme

$(AM)$ passe par le sommet

$E$ et par le centre de gravité

$M$ alors,

$(EM)$ représente la troisième médiane du triangle

$EFG.$

Or, on sait que : dans un triangle, une médiane est une droite qui passe par un sommet et qui coupe le côté opposé à ce sommet en son milieu.

D'où, la droite

$(EM)$ coupe le segment

$[FG]$ en son milieu.

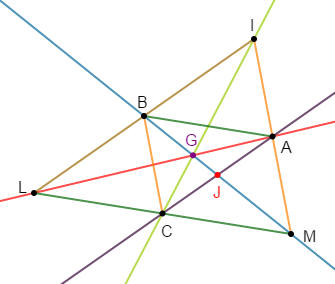
Exercice 21

$MIL$ est un triangle,

$A\;,\ B\$ et

$\ C$ les milieux respectifs des cotés

$[MI]\;,\ [IL]\$ et

$\ [ML].$

Soit

$G$ son centre de gravité.

1) Démontrons que le quadrilatère

$MABC$ est un parallélogramme.

$(AC)\$ et

$\ (MB)$ se coupent en

$J.$

Démontrons que

$J$ est le milieu de

$[AC].$

Dans le triangle

$MIL$ , on a :

$A\;,\ B\$ et

$\ C$ milieux respectifs des côtés

$[MI]\;,\ [IL]\$ et

$\ [ML].$

Donc, en appliquant le théorème de la droite des milieux, on obtient :

$(BC)\parallel(AM)\$ et

$\ (AB)\parallel(MC)$

Ainsi, le quadrilatère

$MABC$ a ses côtés parallèles

$2$ à

$2.$

Par conséquent, c'est un parallélogramme.

D'où, ses diagonales

$[AC]\$ et

$\ [BM]$ se coupent en leur milieu.

Ce qui signifie que

$J$ est le milieu de

$[AC].$

3) Démontrons que

$G$ est le centre de gravité du triangle

$ABC.$

En effet, dans le triangle

$ABC$ , on a :

$(BM)$ passe le sommet

$B$ et par le milieu

$J$ du côté

$[AC].$ Donc, la droite

$(BM)$ est une médiane.

Par ailleurs, en appliquant la même méthode que dans la question

$2)$ , on peut montrer que

$AIBC\$ et

$\ ABLC$ sont des parallélogrammes.

Ainsi, les diagonales

$(CI)\$ et

$\ (AB)$ se coupent en leur milieu. Donc,

$(CI)$ passe par le sommet

$C$ et par le milieu du côté

$[AB].$

Par suite, la droite

$(CI)$ est une médiane du triangle

$ABC$

De la même manière, les diagonales

$(AL)\$ et

$\ (BC)$ se coupent en leur milieu.

Donc,

$(AL)$ passant par le sommet

$A$ , coupe

$[BC]$ par le milieu.

Par conséquent, la droite

$(AL)$ est une médiane du triangle

$ABC$

Ainsi, on constate que ces trois médianes

$(BM)\;,\ (CI)\$ et

$\ (AL)$ se coupent en

$G.$

Or, dans un triangle, les trois médianes se coupent en un point appelé centre de gravité de ce triangle.

Donc,

$G$ est le centre de gravité du triangle

$ABC.$

Exercice 22

$PQR$ est un triangle.

1) Construisons le point

$M$ milieu de

$[PQ]$ et le point

$K$ , symétrique de

$P$ par rapport à

$R.$

La droite

$(KM)$ coupe le segment

$[RQ]$ en

$I$ et la droite

$(PI)$ coupe

$[KQ]$ en

$N.$

2) Démontrons que

$N$ est le milieu du segment

$[KQ].$

Considérons le triangle

$PQK.$

Comme

$K$ est le symétrique de

$P$ par rapport à

$R$ alors,

$R$ est milieu de

$[PK].$

Or,

$M$ est le milieu de

$[PQ]$

Donc, les droites

$(KM)\$ et

$\ (RQ)$ sont des médianes de ce triangle.

Par ailleurs,

$(KM)\$ et

$\ (RQ)$ se coupent en

$I.$

Par conséquent,

$I$ est le centre de gravité du triangle

$PQK.$

Ainsi,

$(PI)$ étant la droite passant par le sommet

$P$ et par le centre de gravité

$I$ alors,

$(PI)$ est la troisième médiane de ce triangle.

Donc, la droite

$(PI)$ coupe

$[KQ]$ par le milieu.

D'où,

$N$ est le milieu du segment

$[KQ].$

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

dim, 06/27/2021 - 13:51

Permalien

Merci

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solution des exercices : Droites remarquables - 4e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Commentaires

Merci

Ajouter un commentaire

Plain text