Solution des exercices : Droites remarquables - 4e
Classe:
Quatrième
Exercice 1
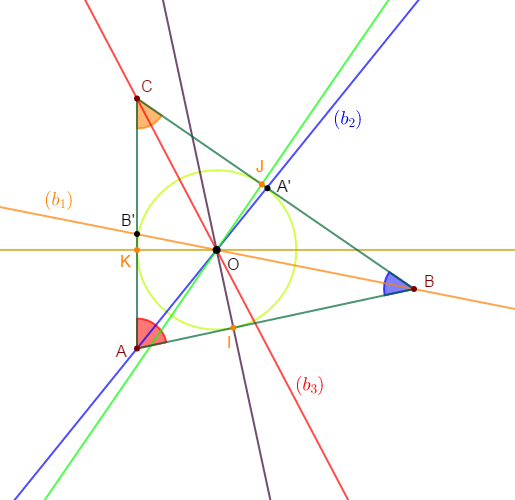
1) Construisons un triangle $ABC$ quelconque.
2) a) Construisons la droite $(b_{2})$ bissectrice de l'angle $\widehat{A}$ ; elle coupe $(BC)$ en $A'.$
b) Construisons la droite $(b_{1})$ bissectrice de l'angle $\widehat{B}$ ; elle coupe $(AC)$ en $B'.$
3) a) $(b_{1})\ $ et $\ (b_{2})$ se coupent en $O$, marquons $O.$
4) a) La droite perpendiculaire à $(AB)$ et passant par $O$ coupe la droite $(AB)$ en $I.$
b) La droite perpendiculaire à $(BC)$ et passant par $O$ coupe la droite $(BC)$ en $J.$
c) La perpendiculaire à $(AC)$ et passant par $O$ coupe la droite $(AC)$ en $K.$
5) a) Démontrons que : $OI=OJ=OK$
En effet, on sait que Si un point $M$ appartient à la bissectrice d'un angle alors, il est équidistant des supports des deux côtés de l'angle.
Or, $O\in(b_{1})$ bissectrice de l'angle $\widehat{B}$ donc, $O$ est équidistant des supports des deux côtés de l'angle $\widehat{B}.$
C'est-à-dire ; $d(O\;,\ (AB)=d(O\;,\ (BC)$
Comme, $d(O\;,\ (AB)=OI\ $ et $\ d(O\;,\ (BC)=OJ$ alors, on obtient : $OI=OJ$
De même, le point $O$ appartient à $(b_{2})$ bissectrice de l'angle $\widehat{A}$ donc, $O$ est équidistant des supports des deux côtés de l'angle $\widehat{A}.$
Ce qui signifie : $d(O\;,\ (AB))=d(O\;,\ (AC))$
Or, $d(O\;,\ (AB))=OI\ $ et $\ d(O\;,\ (AC))=OK$
Par suite, $OI=OK$
Ainsi, $OI=OJ\ $ et $\ OI=OK$
Ce qui donne alors, $$OI=OJ=OK$$
b) En déduisons que $(b_{3})$ bissectrice de $\widehat{C}$ passe par $O.$
On a : $OI=OJ=OK$
Alors, $OJ=OK$
Ce qui signifie : $d(O\;,\ (BC))=d(O\;,\ (AC))$
Donc, le point $O$ est équidistant des supports des deux côtés de l'angle $\widehat{C}.$
Par conséquent, $O$ appartient à la bissectrice $(b_{3})$ de l'angle $\widehat{C}.$
D'où, $(b_{3})$ passe par $O.$
c) Énonçons la propriété que nous venons de démontrer pour les bissectrices.
Propriété : Dans un triangle, les trois bissectrices sont concourantes (se coupent en un même point).
d) Le point $O$ représente le centre du cercle inscrit dans le triangle $ABC$
Exercice 2
Construisons un triangle $MNP$ tel que :
$$MN=6\;cm\;;\ NP=5\;cm\ \text{ et }\ MP=7\;cm$$
1) La bissectrice de l'angle $\widehat{M}$ coupe $[NP]$ en $E.$
2) La bissectrice de l'angle $\widehat{N}$ coupe $(ME)$ en $I.$
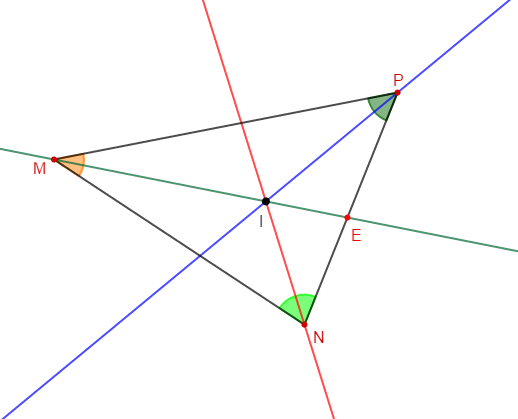
3) Démontrons que $(IP)$ est la bissectrice de l'angle $\widehat{MPN}.$
Comme la bissectrice de l'angle $\widehat{M}$ coupe le segment $[NP]$ en $E$ alors, la droite $(ME)$ représente la bissectrice de l'angle $\widehat{M}.$
De plus, la bissectrice de l'angle $\widehat{N}$ coupe $(ME)$ en $I.$
Cela signifie que la bissectrice de l'angle $\widehat{M}$ et bissectrice de l'angle $\widehat{N}$ se rencontrent en $I.$
Or, dans un triangle, les trois bissectrices se coupent en un même point.
Par conséquent, la troisième bissectrice, celle de l'angle $\widehat{P}$, passe aussi par le point $I.$
Ce qui montre que $(IP)$ est la bissectrice de l'angle $\widehat{MPN}.$
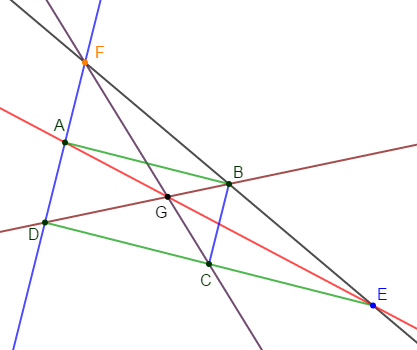
La droite $(RO)$ passe par $R$ et par $O$ centre de gravité du triangle $RDK$ donc, $(RO)$ est une médiane.
Exercice 3
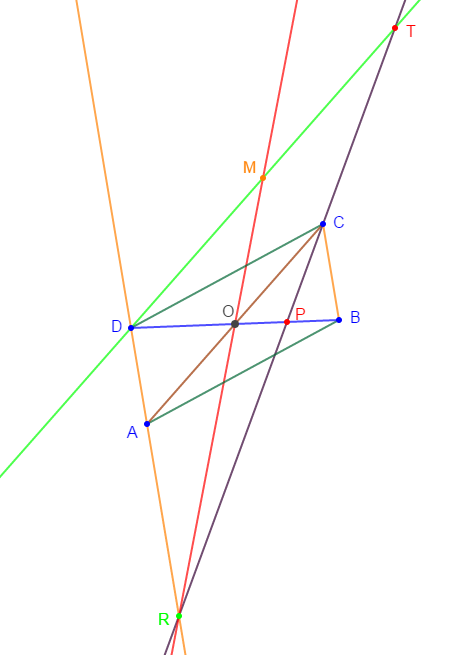
$ABCD$ est un parallélogramme de centre $O\;,\ P$ est le milieu de $[OB].$
Les droites $(CP)\ $ et $\ (DA)$ se coupent en $R.$
$T$ est le symétrique de $R$ par rapport à $P$
Les droites $(RO)\ $ et $\ (DT)$ se coupent en $M.$
1) Faisons une figure complète.

2) Montrons que $(DP)$ est une médiane de $RDT.$
Comme $T$ est le symétrique de $R$ par rapport à $P$ alors, $P$ est le milieu de $[RT]$
Or, la droite $(DP)$ passe par le sommet $D$ du triangle $RDT$ et par milieu $P$ du côté opposé à ce sommet.
Donc, $(DP)$ est une médiane de $RDT.$
3) Montrons que $DO=\dfrac{2}{3}DP$
On a : $DO+OP=DP$
Or, $P$ est milieu de $[OB]$ ce qui signifie que $OP=\dfrac{1}{2}OB$
Donc, en remplaçant $OP$ par $\dfrac{1}{2}OB$, on obtient :
$$DO+OP=DO+\dfrac{1}{2}OB=DP$$
Par ailleurs, $O$ est le centre du parallélogramme $ABCD$ donc, $O$ est le milieu des deux diagonales de $ABCD.$
Ainsi, $O$ est milieu de $DB$
Alors, $OB=DO$
Donc, en remplaçant $OB=DO$, on obtient :
$$DO+\dfrac{1}{2}OB=DO+\dfrac{1}{2}DO=DP$$
Par suite,
$\begin{array}{rcl} DO+\dfrac{1}{2}DO=DP&\Rightarrow&\dfrac{2DO}{2}+\dfrac{DO}{2}=DP\\\\&\Rightarrow&\dfrac{2DO+DO}{2}=DP\\\\&\Rightarrow&\dfrac{3DO}{2}=DP\\\\&\Rightarrow&3DO=2DP\\\\&\Rightarrow&DO=\dfrac{2}{3}DP\end{array}$
D'où, $\boxed{DO=\dfrac{2}{3}DP}$
4) $O$ est le centre de gravité du triangle $RDT.$
En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.
Or, le point $O$ situé sur la médiane issue de $D$ vérifie :
$$DO=\dfrac{2}{3}DP$$
Par conséquent, $O$ est le centre de gravité du triangle $RDT.$
5) Démontrons que $M$ est milieu du segment $[DT].$
La droite $(RO)$ passe par $R$ et par $O$ centre de gravité du triangle $RDK$ donc, $(RO)$ est une médiane.
On sait que : dans un triangle, une médiane est une droite passant un sommet et par le milieu du côté opposé à ce sommet.
Or, le côté opposé au sommet $R$ est le segment $[DT]$ et que $(RO)$ coupe $(DT)$ en $M.$
Par conséquent, $M$ est milieu de $[DT].$
Exercice 4
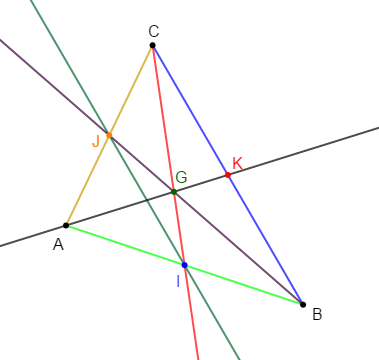
1) Construisons un triangle $ABC$ tel que :
$AB=5\;cm\;,\ AC=4\;cm\ $ et $\ BC=6\;cm.$
$I\ $ et $\ J$ sont les milieux respectifs de $[AB]\ $ et $\ [AC].$
2) Montrons que les droites $(IJ)\ $ et $\ (BC)$ sont parallèles puis calculons $IJ.$
Considérons le triangle $ABC$, on remarque alors que la droite $(IJ)$ passe par les points $I\ $ et $\ J$ milieux respectifs des côtés $[AB]\ $ et $\ [AC].$
Donc, d'après le théorème de la droite des milieux les droites $(IJ)\ $ et $\ (BC)$ sont parallèles.
Par ailleurs, d'après une conséquence du théorème de la droite des milieux, on a :
$$IJ=\dfrac{BC}{2}$$
Par suite, en remplaçant $BC$ par sa valeur, on obtient : $IJ=\dfrac{6}{2}=3$
D'où, $\boxed{IJ=3\;cm}$
3) Les demi-droites $[BJ)\ $ et $\ [CI)$ se coupent en $G.$
a) Les demi-droites $[BJ)\ $ et $\ [CI)$ sont des médianes du triangle $ABC$
b) Le point $G$ est le centre de gravité du triangle $ABC$
4) Soit $K$ le milieu du segment $[BC].$ Montrons que les points $A\;,\ G\ $ et $\ K$ sont alignés.
En effet, la droite $(AK)$ passe par le sommet $A$ et par $K$ ; milieu du côté opposé à ce sommet.
Par conséquent, $(AK)$ est une médiane du triangle $ABC.$
Or, $G$ est le centre de gravité du triangle $ABC$ donc, la droite $(AK)$ passe par $G.$
Par suite, $A\;,\ G\ $ et $\ K$ appartiennent à la même droite $(AK).$
D'où, les points $A\;,\ G\ $ et $\ K$ sont alignés.
5) On donne $AK=3\;cm$. Calculons $AG\ $ et $\ GK.$
En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.
Ce qui signifie que :
$$AG=\dfrac{2}{3}AK$$
Donc, en remplaçant $AK$ par sa valeur, on obtient : $AG=\dfrac{2\times 3}{3}=2$
Ainsi, $\boxed{AK=2\;cm}$
Par ailleurs, on a : $G\in[AK]$ alors, $AG+GK=AK$
Par suite,
$\begin{array}{rcl} GK&=&AK-AG\\\\&=&3-2\\\\&=&1\end{array}$
D'où, $\boxed{GK=1\;cm}$

Exercice 5
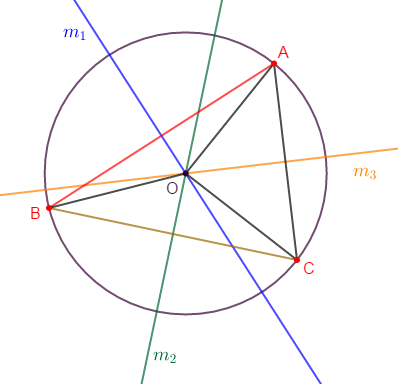
1) Construisons un triangle $ABC$ quelconque.
2) a) Construisons la droite $(m_{1})$ médiatrice de $[AB].$
b) Construisons la droite $(m_{2})$ médiatrice de $[BC].$
2) a) Les droites $(m_{1})\ $ et $\ (m_{2})$ se coupent en $O.$
3) a) Démontrons que : $OA=OB=OC.$
On a : $(m_{1})$ médiatrice de $[AB]\ $ et $\ O\in(m_{1})$
En effet, on sait que : si un point appartient à la médiatrice d'un segment alors, ce point est à égale distance des extrémités de ce segment.
Or, $O\in(m_{1})$ médiatrice du segment $[AB]$ donc, $O$ est équidistant des extrémités $A\ $ et $\ B$ de ce segment.
Ce qui se traduit par :
$$OA=OB$$
De la même manière, comme $O\in(m_{2})$ médiatrice du segment $[BC]$ alors, $O$ est à égale distance des extrémités $B\ $ et $\ C$ de ce segment.
Ce qui peut s'écrire :
$$OB=OC$$
Ainsi, on a : $OA=OB\ $ et $\ OB=OC$
D'où, $\boxed{OA=OB=OC}$
b) En déduisons que la droite $(m_{3})$ médiatrice de $[AC]$ passe par $O.$
En effet, on sait que tout point situé à égale distance des extrémités d'un segment appartient à la médiatrice de ce segment.
Or, d'après le résultat de 3) a) on a :
$$OC=OA$$
Ce qui signifie que le point $O$ est à égale distance des points $A\ $ et $\ C.$
Par conséquent, $O$ appartient à la médiatrice du segment $[AC].$
D'où, la droite $(m_{3})$ médiatrice de $[AC]$ passe par $O.$
c) Énonçons la propriété que nous venons de démontrer pour les médiatrices.
Dans un triangle, les médiatrices des côtés se coupent en un point.
d) Le point $O$ est le centre du cercle circonscrit au triangle $ABC$

Exercice 6
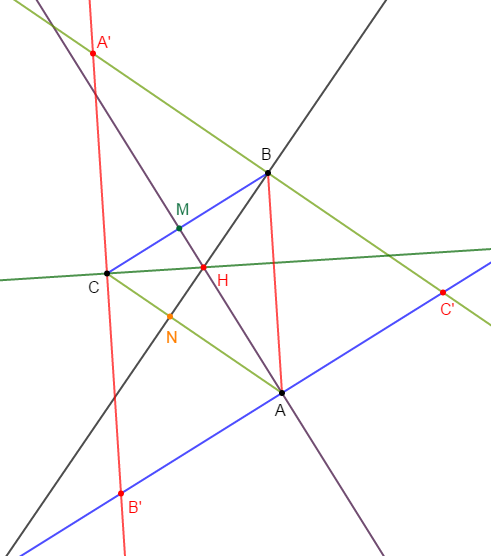
1) Construisons un triangle $ABC$ quelconque.
2) a) Construisons $(AM)$ hauteur issue de $A.$
b) Construisons la droite $(BN)$ hauteur issue de $B.$
3) Les deux droites $(AM)\ $ et $\ (BN)$ se coupent en $H$, plaçons le point $H.$
4) a) Construisons la droite $(B'C')$ passant par $A$ et parallèle à $(BC).$
b) Construisons la droite $(A'C')$ passant par $B$ et parallèle à $(AC).$
c) Construisons la droite $(B'A')$ passant par $C$ et parallèle à $(AB).$
5) Démontrons que les quadrilatères $ABCB'\;;\ BCAC'\ $ et $\ CABA'$ sont des parallélogrammes.
On a : $(B'C)\parallel(AB)\ $ et $\ (BC)\parallel(B'A)$
Donc, le quadrilatère $ABCA'$ a ses côtés parallèles $2$ à $2.$
Par conséquent, $ABCA'$ est un parallélogramme.
On a : $(BC)\parallel(AC')\ $ et $\ (AC)\parallel(BC')$
Donc, le quadrilatère $BCAC'$ a ses côtés parallèles $2$ à $2.$
D'où, $BCAC'$ est un parallélogramme.
On a : $(A'C)\parallel(AB)\ $ et $\ (AC)\parallel(A'B)$
Donc, le quadrilatère $CABA'$ a ses côtés parallèles $2$ à $2.$
Par conséquent, $CABA'$ est un parallélogramme.
6) a) Démontrons que $(AH)$ est la médiatrice de $[B'C'].$
En effet, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est aussi perpendiculaire à l'autre.
Or, dans le triangle $ABC$, on a : $(AH)$ hauteur issue de $A$ donc, $(AH)$ perpendiculaire à $(BC).$
De plus, $(BC)\parallel(B'C')$
Par suite, $(AH)$ est perpendiculaire à $(B'C').$
Par ailleurs, $ABCB'\ $ et $\ ABCB'$ sont des parallélogrammes alors, $BC=AC'\ $ et $\ BC=AC'.$
Or, $B'\;,\ A\ $ et $\ C'$ alignés donc, $A$ est milieu de $[B'C']$
Ainsi, $(AH)$ est perpendiculaire à $[B'C']$ et passe par le milieu de ce segment.
Par conséquent, $(AH)$ est la médiatrice de $[B'C'].$
b) Démontrons que $(BH)$ est la médiatrice de $[A'C'].$
Dans le triangle $ABC$, on a : $(BH)$ hauteur issue de $B$ alors, $(BH)$ est perpendiculaire à $(AC).$
Or, $(AC)$ est parallèle à $(A'C').$
Donc, $(BH)$ est perpendiculaire à $(A'C').$
De plus, comme $CABA'\ $ et $\ BCAC'$ sont des parallélogrammes alors, on a : $AC=A'B\ $ et $\ AC=BC'.$
Or, les points $A'\;,\ B\ $ et $\ C'$ sont alignés donc, $B$ est milieu de $[A'C']$
Ainsi, $(BH)$ est perpendiculaire à $[A'C']$ et passe par le milieu de ce segment.
Par conséquent, $(BH)$ est la médiatrice de $[A'C'].$
c) Démontrons que $(CH)$ est la troisième médiatrice du triangle $A'B'C'.$
On a :
$H$ appartient à la médiatrice de $[B'C']$ alors, $HB'=HC'$
$H$ appartient à la médiatrice de $[A'C']$ alors, $HA'=HC'$
Ainsi, $HB'=HC'\ $ et $\ HA'=HC'$
Par suite, $HB'=HA'$ ce qui signifie que $H$ est situé à égale distance des points $A'\ $ et $\ B'.$
Or, on sait que tout point situé à égale distance des extrémités d'un segment appartient à la médiatrice de ce segment.
Donc, $H$ appartient à la médiatrice de $[A'B'].$
De plus, $C$ est milieu de $[A'B'].$
Par conséquent, $(CH)$ est la troisième médiatrice du triangle $A'B'C'.$
7) a) Les médiatrices du triangle $A'B'C'$ représentent les hauteurs du triangle $ABC$
b) Énonçons la propriété que nous venons de démontrer pour les hauteurs du triangle.
Dans un triangle, les trois hauteurs se coupent en un point.
c) Le point $H$ représente l'orthocentre du triangle $ABC$

Exercice 7
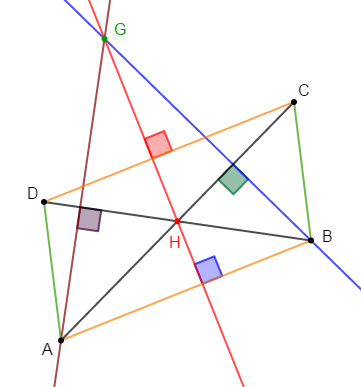
Soit $ABCD$ un parallélogramme de centre $H.$
La perpendiculaire à $(DB)$ passant par $A$ et la perpendiculaire à $(AC)$ passant par $B$ se coupent en $G.$
1) Faisons une figure.

2) Le point $H$ est l'orthocentre du triangle $AGB.$
3) Montrons que les droites $(GH)\ $ et $\ (AB)$ sont perpendiculaires.
Comme $H$ est l'orthocentre de $AGB$ alors, la droite $(GH)$ passant par le sommet $G$ et par $H$ est hauteur du triangle $AGB.$
Par suite, $(GH)$ est perpendiculaire au côté opposé au sommet $G.$
D'où, les droites $(GH)\ $ et $\ (AB)$ sont perpendiculaires.
4) Montrons que les droites $(GH)\ $ et $\ (DC)$ sont perpendiculaires.
En effet, comme $ABCD$ est un parallélogramme alors, les droites $(AB)\ $ et $\ (DC)$ sont parallèles.
De plus, d'après le résultat de $3)$, les droites $(GH)\ $ et $\ (AB)$ sont perpendiculaires.
Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est aussi perpendiculaire à l'autre.
Par conséquent, les droites $(GH)\ $ et $\ (DC)$ sont perpendiculaires.
Exercice 8
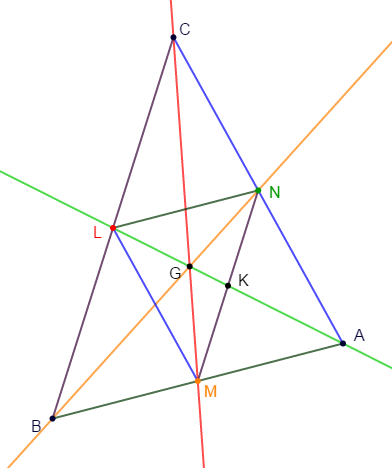
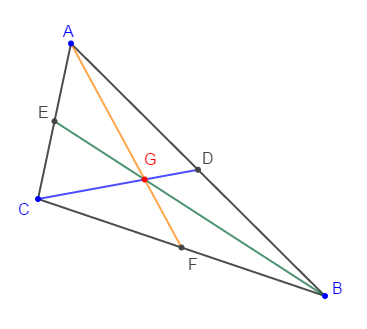
Soit $ABC$ un triangle tel que :
$AB=6\;cm\;;\ AC=7\;cm\ $ et $\ BC=8\;cm.$
Les points $L\;,\ M\ $ et $\ N$ sont les milieux respectifs des côtés $[BC]\;,\ [AB]\ $ et $\ [AC]$ du triangle.
$G$ est le centre de gravité.
1) Faisons une figure complète.

2) Démontrons que $MLNA$ est un parallélogramme. Soit $K$ sont centre.
Considérons le triangle $ABC.$
On a : $M\ $ et $\ L$ milieux respectifs des côtés $[AB]\ $ et $\ [BC].$
Donc, d'après le théorème de la droite des milieux la droite $(ML)$ passant par $M\ $ et $\ L$ est parallèle à la droite $(AC).$
Par suite, $(ML)$ est parallèle à $(AN)$
De la même manière, on a : $N\ $ et $\ L$ milieux respectifs des côtés $[AC]\ $ et $\ [BC].$
Alors, d'après le théorème de la droite des milieux la droite $(NL)$ passant par $N\ $ et $\ L$ est parallèle à la droite $(AC).$
Donc, $(NL)$ est parallèle à $(AM)$
Ainsi, on a : $(ML)\parallel(AN)\ $ et $\ (NL)\parallel(AM)$
Donc, le quadrilatère $MLNA$ a ses côtés parallèles $2$ à $2.$
Par conséquent, c'est un parallélogramme.
En déduisons que : $AK=\dfrac{1}{2}AL$ puis $KG=\dfrac{1}{6}AL$
Comme $K$ est le centre du parallélogramme $MLNA$ alors, $K$ est milieu de $[AL].$
D'où, $\boxed{AL=\dfrac{1}{2}AL}$
Par ailleurs, $G$ étant le centre de gravité du triangle $ABC$ donc,
$$AG=\dfrac{2}{3}AL$$
Comme $K\in[AG]$ alors, on a : $KG+AK=AG$
Donc, $KG=AG-AK$
Par suite, en remplaçant $AG\ $ et $\ AK$ par leur expression, on obtient :
$\begin{array}{rcl} KG&=&AG-AK\\\\&=&\dfrac{2}{3}AL-\dfrac{1}{2}AL\\\\&=&\dfrac{4}{6}AL-\dfrac{3}{6}AL\\\\&=&\dfrac{1}{6}AL\end{array}$
D'où, $\boxed{KG=\dfrac{1}{6}AL}$
Exercice 9
Soit $ABCD$ un parallélogramme et $E$ le symétrique de $D$ par rapport à $C.$ Les droites $(AD)\ $ et $\ (BE)$ se coupent en $F.$
1) Montrons que $B$ est le milieu du segment $[EF].$
Considérons le triangle $DEF.$
On a : $E$ le symétrique de $D$ par rapport à $C$ donc, $C$ est milieu de $[DE].$
Comme $ABCD$ est un parallélogramme alors, $(BC)$ est parallèle à $(AD).$
C'est à dire $(BC)\ $ et $\ (DF)$ sont parallèles.
Ainsi, d'après le théorème de la droite des milieux, la droite $(BC)$ passant par le milieu de $[DE]$ et parallèle à $(DF)$ coupe $[FE]$ en son milieu.
Par conséquent, $B$ est le milieu du segment $[EF].$
2) Montrons que $A$ est le milieu du segment $[DF].$
Comme $ABCD$ est un parallélogramme alors, $(AB)\ $ et $(DC)$ sont parallèles.
C'est à dire $(AB)$ parallèle à $(DE).$
En considérant le triangle $DEF$, on remarque que la droite $(AB)$ passant par $B$ milieu de $[EF]$ et parallèle à $(DE)$, coupe $[DF]$ en $A.$
Donc, en appliquant le théorème de la droite des milieux dans ce triangle, on obtient : $A$ milieu de $[DF].$
3) Les droites $(FC)\ $ et $\ (DB)$ se coupent en $G.$ Démontrons que les points $A\;,\ G\ $ et $\ E$ sont alignés.
En effet, $(FC)\ $ et $\ (DB)$ sont deux médianes du triangle $DEF.$
Donc, $G$ est le centre de gravité de ce triangle.
Comme la droite $(AE)$ passe par le sommet $E$ et par le milieu $A$ du segment $[DF]$ alors, $(AE)$ est la troisième médiane du triangle $DEF.$
Par conséquent, elle passe par le point $G.$
Ainsi, les points $A\;,\ G\ $ et $\ E$ appartiennent à une même droite.
Ce qui montre que ces points sont alignés.

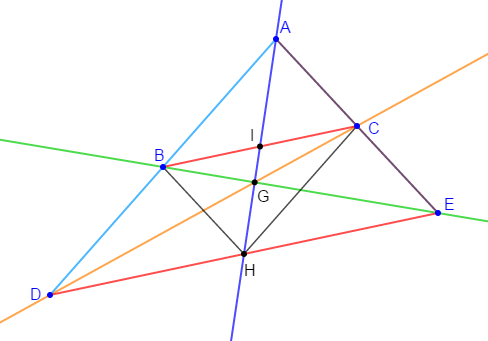
Exercice 10
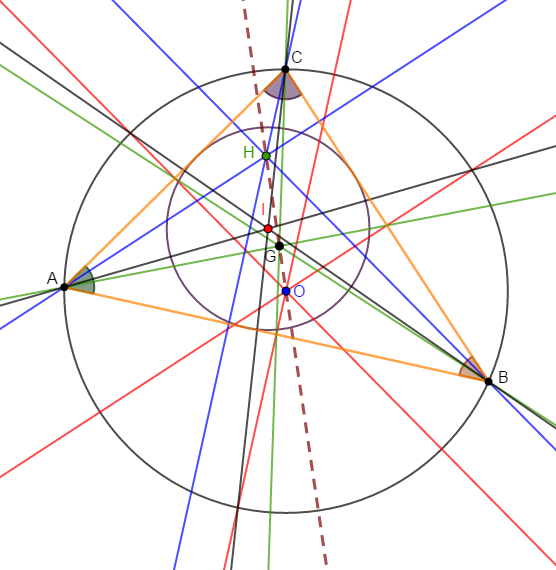
1) Construisons un triangle $ABC$ tel que $AB=14\;cm\;,\ AC=10\;cm\ $ et $\ BC=12\;cm.$
2) Construisons ses médiatrices en rouge, ses médianes en vert, ses hauteurs en bleu et ses bissectrices en noir.
3) Plaçons le point $G$ centre de gravité du triangle, le point $O$ centre du cercle circonscrit, le point $I$ centre du cercle inscrit et le point $H$ orthocentre du triangle.
4) Pour ce triangle $ABC$, construisons les cercles circonscrit et inscrit.
5) Traçons la droite qui passe par $O\ $ et $\ G.$
Nous constatons que cette droite passe par $H.$

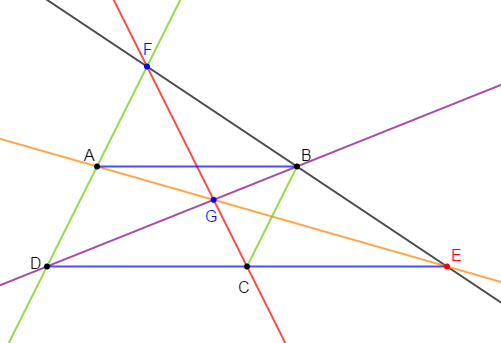
Exercice 11
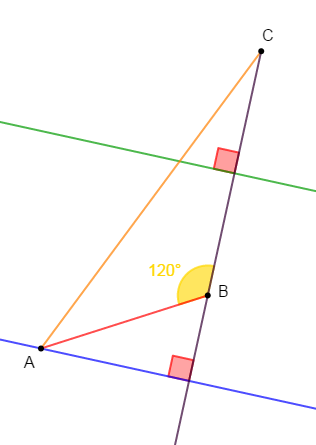
Construis le triangle $ABC$ tel que :
$AB=3.5\;cm\;,\ \widehat{ABC}=120^{\circ}\ $ et $\ BC=5\;cm.$
1) Traçons en bleu la hauteur issue de $A$ et en vert la médiatrice du segment $[BC].$

2) Démontrons que ces deux droites sont parallèles.
En effet, la hauteur issue de $A$ est la droite passant par $A$ et perpendiculaire au côté opposé au sommet $A.$
Donc, la hauteur est perpendiculaire à la droite $(BC).$
Par ailleurs, la médiatrice du segment $[BC]$ est la droite perpendiculaire à la droite $(BC)$ et passant par le milieu du segment $[BC].$
Or, on sait que : si deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.
D'où, la hauteur issue de $A$ et la médiatrice de $[BC]$ sont parallèles.
Exercice 12
$ABC$ est un triangle de centre de gravité $G.$
$E\;,\ D\ $ et $\ F$ sont les milieux respectifs de $[AC]\;,\ [AB]\ $ et $\ [BC].$

On donne :
$AE=2\;cm\;,\ AG=3\;cm\;,\ GD=1\;cm\ $ et $\ BE=6\;cm.$
Calculons $AC\;,\ GF\;,\ GC\;,\ BG\ $ et $\ GE.$
$-\ $ Calcul de $AC$
Comme $E$ est milieu de $[AC]$ alors, $AC=2AE.$
Donc, en remplaçant $AE$ par sa valeur, on obtient : $AC=2\times 2=4$
D'où, $\boxed{AC=4\;cm}$
$-\ $ Calcul de $GF$
En effet, on sait que le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.
Donc, $AG=\dfrac{2AF}{3}$
Par suite,
Comme $AG+GF=AF$ alors, $GF=AF-AG$
En remplaçant $AG$ par son expression, on obtient :
$\begin{array}{rcl} GF&=&AF-AG\\\\&=&AF-\dfrac{2AF}{3}\\\\&=&\dfrac{3AF}{3}-\dfrac{2AF}{3}\\\\&=&\dfrac{AF}{3}\end{array}$
Donc, $GF=\dfrac{AF}{3}$
Ainsi, on a :
$$\left\lbrace\begin{array}{rcl} AG&=&2\times\dfrac{AF}{3}\\\\GF&=&\dfrac{AF}{3}\end{array}\right.\ \Rightarrow\ AG=2GF$$
Par suite, $GF=\dfrac{AG}{2}=\dfrac{3}{2}=1.5$
D'où, $\boxed{GF=1.5\;cm}$
$-\ $ Calcul de $GC$
En procédant de la même manière que dans le calcul précédent, on obtient :
$$\left\lbrace\begin{array}{rcl} GC&=&2\times\dfrac{CD}{3}\\\\GD&=&\dfrac{CD}{3}\end{array}\right.\ \Rightarrow\ GC=2GD$$
Par suite, $GC=2\times 1=2$
Ainsi, $\boxed{GC=2\;cm}$
$-\ $ Calcul de $BG$
Comme le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet alors, on a : $GB=\dfrac{2BE}{3}$
Ce qui donne : $GB=\dfrac{2\times 6}{3}=\dfrac{12}{3}=4$
Ainsi, $\boxed{GB=4\;cm}$
$-\ $ Calcul de $GE$
On a : $GE+GB=BE$ donc, $GE=BE-GB$
Ainsi, $GE=6-4=2$
D'où, $\boxed{GE=2\;cm}$
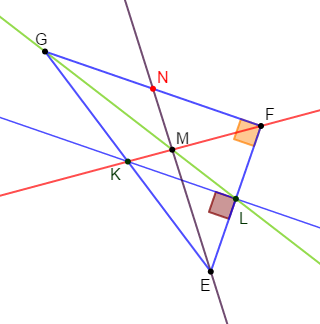
Exercice 13
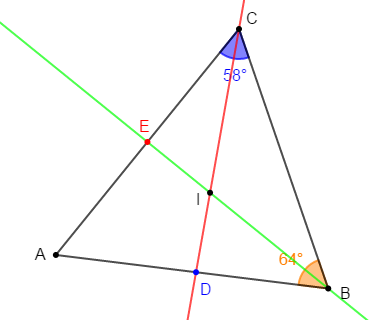
Sur la figure ci-dessous, $\widehat{ABC}=64^{\circ}\ $ et $\ \widehat{ACB}=58^{\circ}.$
$(BE)$ est la bissectrice de l'angle $\widehat{B}\ $ et $\ (CD)$ est la bissectrice de l'angle $\widehat{C}.$
Les deux bissectrices se coupent en $I.$

Calculons la mesure des angles $\widehat{ACD}\;,\ \widehat{ADC}\;,\ \widehat{BIC}\;,\ \widehat{BAC}.$
$-\ $ Calcul de la mesure de l'angle $\widehat{ACD}$
Comme $(CD)$ est la bissectrice de l'angle $\widehat{C}$ alors, $(CD)$ partage cet angle en deux angles de même mesure : $\widehat{ACD}\ $ et $\ \widehat{DCB}$
Ainsi,
$$\widehat{ACD}=\widehat{DCB}=\dfrac{\widehat{ACB}}{2}$$
Par suite,
$\begin{array}{rcl}\widehat{ACD}&=&\dfrac{\widehat{ACB}}{2}\\\\&=&\dfrac{58^{\circ}}{2}\\\\&=&29^{\circ}\end{array}$
D'où, $\boxed{\widehat{ACD}=29^{\circ}}$
$-\ $ Calcul de la mesure de l'angle $\widehat{BAC}.$
On sait que dans un triangle, la somme des angles est égale à $180^{\circ}.$
Donc, dans le triangle $ABC$, on a :
$$\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^{\circ}$$
Par suite, $\widehat{BAC}=180^{\circ}-\widehat{ACB}-\widehat{ABC}$
Ainsi,
$\begin{array}{rcl}\widehat{BAC}&=&180^{\circ}-58^{\circ}-64^{\circ}\\\\&=&58^{\circ}\end{array}$
D'où, $\boxed{\widehat{BAC}=58^{\circ}}$
$-\ $ Calcul de la mesure de l'angle $\widehat{ADC}$
Comme la somme des angles d'un triangle est égale à $180^{\circ}$ alors, en considérant le triangle $ADC$, on a :
$$\widehat{ADC}+\widehat{ACD}+\widehat{DAC}=180^{\circ}$$
Ce qui donne : $\widehat{ADC}=180^{\circ}-\widehat{ACD}-\widehat{DAC}$
Par suite,
$\begin{array}{rcl}\widehat{ADC}&=&180^{\circ}-29^{\circ}-58^{\circ}\\\\&=&93^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{ADC}=93^{\circ}}$
$-\ $ Calcul de la mesure de l'angle $\widehat{BIC}$
En considérant le triangle $BIC$, on a :
$$\widehat{BIC}+\widehat{ICB}+\widehat{CBI}=180^{\circ}$$
Comme $(BE)$ est la bissectrice de l'angle $\widehat{B}$ alors, $(BE)$ partage cet angle en deux angles de même mesure.
Ainsi, $\widehat{CBI}=\dfrac{\widehat{ABC}}{2}=\dfrac{64^{\circ}}{2}=32^{\circ}$
Par ailleurs, on a : $\widehat{ICB}=\widehat{DCB}\ $ et $\ \widehat{DCB}=\widehat{ACD}=29^{\circ}$
Donc, $\widehat{ICB}=29^{\circ}$
Alors, les angles du triangle $BIC$ vérifient :
$$\widehat{BIC}+29^{\circ}+32^{\circ}=180^{\circ}$$
Par suite
$\begin{array}{rcl}\widehat{BIC}&=&180^{\circ}-29^{\circ}-32^{\circ}\\\\&=&119^{\circ}\end{array}$
D'où, $\boxed{\widehat{BIC}=119^{\circ}}$

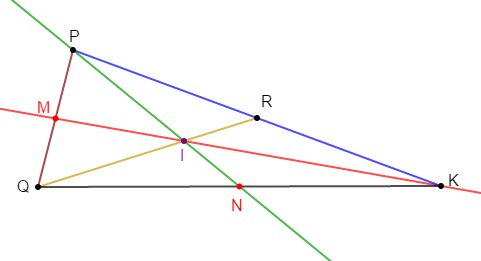
Exercice 14
On donne un segment $[AK].$
Soit $J$ son milieu.
Plaçons un point $L$ n'appartenant pas à $(AK)$ tel que $JL=6\;cm.$
Plaçons sur $[JL]$ le point $G$ tel que $LG=4\;cm.$
$(KG)$ coupe $(AL)$ en $I.$
Démontons que $I$ est le milieu de $[AL].$
Considérons le triangle $AKL.$
Comme $J$ est milieu de $[AK]$ alors, $[LJ)$ est la médiane issue de $L.$
Par ailleurs, en calculant le rapport $\dfrac{LG}{JL}$, on trouve : $\dfrac{LG}{JL}=\dfrac{4}{6}=\dfrac{2}{3}$
Donc, $\dfrac{LG}{JL}=\dfrac{2}{3}$
Par suite, $LG=\dfrac{2}{3}JL$
Ainsi, le point $G$ est situé au deux tiers de $[LJ]$, à partir du sommet $L.$
Ce qui signifie que $G$ est le centre de gravité du triangle $AKL.$
Par conséquent, la droite $(KG)$, passant par le sommet $K$ et par $G$, est aussi une médiane de ce triangle.
De plus, $(KG)$ coupe $[AL]$ en $I.$
Or, on sait que : dans un triangle, une médiane issue d'un sommet, coupe le côté opposé à ce sommet en son milieu.
D'où, $I$ est le milieu de $[AL].$

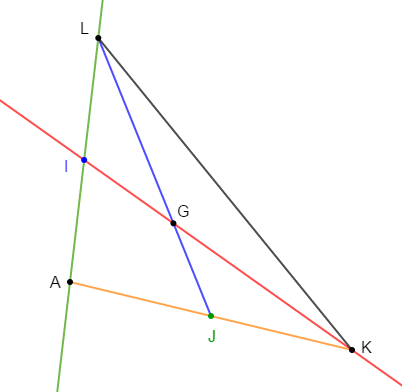
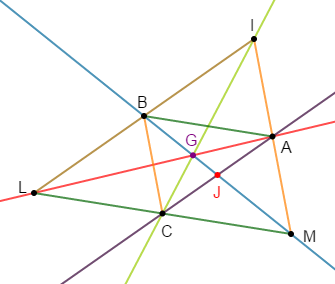
Exercice 15
$MNP$ est un triangle isocèle en $M\;,\ K$ est le milieu de $[NP].$
Les bissectrices $(PZ)\ $ et $\ (NT)$ des angles $\widehat{MPN}\ $ et $\ \widehat{MNP}$ se coupent en $I.$
Démontrons que $(MK)$ passe par $I.$
En effet, la droite $(MK)$ passant le sommet $M$, coupe $[PN]$ par le milieu $K.$ Donc, $(MK)$ est aussi médiane du triangle $MNP.$
Comme le triangle $MNP$ est isocèle en $M$ alors, la médiane $(MK)$ issue de $M$ est aussi bissectrice de l'angle $\widehat{PMN}.$
De plus, on sait que : dans un triangle, les trois bissectrices se coupent en un point.
Or, les deux bissectrices $(PZ)\ $ et $\ (NT)$ se coupent en $I.$
Par conséquent, la troisièmes bissectrice $(MK)$ passe alors par $I.$

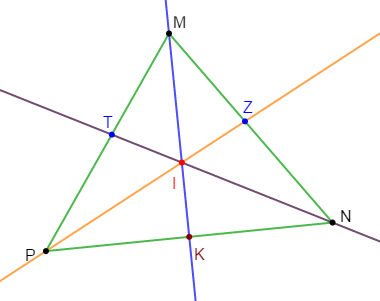
Exercice 16
$KELI$ est un parallélogramme de centre $O.$
1) Construisons le point $M$ centre de gravité du triangle $KEI$ et le point $N$ centre de gravité du triangle $ILE.$

2) Démontre que les points $K\;,\ M\;,\ O\;,\ N\ $ et $\ L$ sont alignés.
En effet, $KELI$ étant un parallélogramme de centre $O$ alors, ses diagonales $[IE]\ $ et $\ [KL]$ ont même milieu $O.$
Dans le triangle $KEI$, on a : $(KL)$ passe par le sommet $K$ et par le milieu $O$ du côté opposé à ce sommet donc, $(KL)$ est une médiane de ce triangle.
Donc, $(KL)$ passe par le centre de gravité $M$ du triangle $KEI.$
Par suite, $K\;,\ M\;,\ O$ appartiennent à la même droite $(KL).$
De la même manière, en considérant le triangle $ILE$, on a : $(KL)$ passe par $L\ $ et $\ O$ donc, la droite $(KL)$ est une médiane de ce triangle.
Elle passe alors par le centre de gravité $N$ du triangle $ILE.$
Par suite, $L\;,\ N\;,\ O$ appartiennent à la même droite ($KL).$
Ainsi, $K\;,\ M\;,\ O\;,\ N\;,\ L$ appartiennent tous à la même droite $(KL).$
Par conséquent, ces points sont alignés.
3) Démontrons que $KM=MN=NL.$
En effet, on sait que : le centre de gravité d'un triangle est situé au deux tiers de chaque médiane, à partir du sommet.
Donc :
dans le triangle $KEI$, on a : $KM=\dfrac{2}{3}KO$
dans le triangle $ILE$, on a : $NL=\dfrac{2}{3}LO$
Or, le point $O$ est milieu de $[KL]$ donc, $KO=LO=\dfrac{KL}{2}$
Ainsi, en remplaçant $KO\ $ et $\ LO$ par $\dfrac{KL}{2}$, on obtient :
$\begin{array}{rcl} KM&=&\dfrac{2}{3}KO\\\\&=&\dfrac{2}{3}\times\dfrac{KL}{2}\\\\&=&\dfrac{KL}{3}\end{array}$
Donc, $\boxed{KM=\dfrac{KL}{3}}$
$\begin{array}{rcl} NL&=&\dfrac{2}{3}LO\\\\&=&\dfrac{2}{3}\times\dfrac{KL}{2}\\\\&=&\dfrac{KL}{3}\end{array}$
Ainsi, $\boxed{NL=\dfrac{KL}{3}}$
Par ailleurs, on a : $KM+MN+NL=KL$
Ce qui donne alors, $MN=KL-KM-NL$
Donc, en remplaçant $KM\ $ et $\ NL$ par $\dfrac{KL}{3}$, on obtient :
$\begin{array}{rcl} MN&=&KL-KM-NL\\\\&=&KL-\dfrac{KL}{3}-\dfrac{KL}{3}\\\\&=&KL-\dfrac{2KL}{3}\\\\&=&\dfrac{3KL}{3}-\dfrac{2KL}{3}\\\\&=&\dfrac{KL}{3}\end{array}$
Donc, $\boxed{MN=\dfrac{KL}{3}}$
Ainsi, on a : $\left\lbrace\begin{array}{rcl} KM=\dfrac{KL}{3}\\\\MN=\dfrac{KL}{3}\\\\MN=\dfrac{KL}{3}\end{array}\right.$
Par conséquent, $\boxed{KM=MN=NL}$
Exercice 17
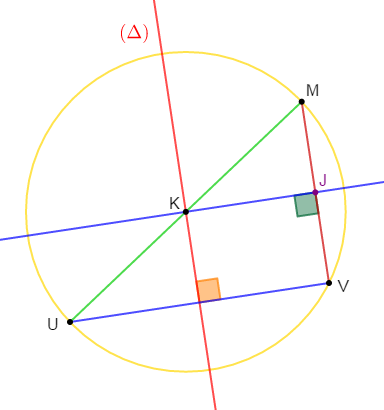
1) Construisons un segment $[UV]$ et sa médiatrice $(\Delta).$
Marquons un point $K$ sur cette médiatrice, $K$ n'appartient pas à $[UV]$ et le point $M$ symétrique de $U$ par rapport à $K.$
2) Démontrons que $K$ est le centre du cercle circonscrit au triangle $MUV.$
On considère le triangle $MUV.$
On a : $(\Delta)$ médiatrice de $[UV]$ alors, $(\Delta)$ est perpendiculaire à $(UV)$ et passe par le milieu de $[UV].$
Par ailleurs, $M$ symétrique de $U$ par rapport à $K$ donc, $K$ est milieu de $[MU].$
Ainsi, d'après le théorème de la droite des milieux, $(\Delta)$ est parallèle à $(MV).$
Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Donc, $(UV)$ est perpendiculaire à $(MV).$
D'où, $MUV$ est un tringle rectangle en $V.$
Par conséquent, le centre du cercle circonscrit est le milieu $K$ de l'hypoténuse $[MU].$
3) La parallèle à $(UV)$ passant par $K$ coupe $(MV)$ en $J.$
Démontrons que $(KJ)$ est la médiatrice du segment $[MV].$
En effet, considérons le triangle $MUV.$
Comme $K$ est milieu de $[MU]$ alors, d'après la réciproque du théorème de la droite des milieux, la parallèle à $(UV)$ passant par $K$ coupe $[MV]$ en son milieu.
Donc, $J$ est milieu de $[MV]$
Par ailleurs, comme $(KJ)$ est parallèle à $(UV)\ $ et $\ (MV)$ est perpendiculaire à $(UV)$ alors, $(KJ)$ est perpendiculaire à $(MV).$
Ainsi, on a : $(KJ)$ est perpendiculaire à $(MV)$ et passe par le milieu de $[MV].$
Par conséquent, $(KJ)$ est la médiatrice du segment $[MV].$

Exercice 18
Traçons un triangle $ABC.$
On appelle $D$ le symétrique de $A$ par rapport à $B$ et $E$ le symétrique de $A$ par rapport à $C.$
1) Démontrons que les droites $(BC)$ et $(DE)$ sont parallèles.
Considérons le triangle $ADE.$
On a :
$D$ symétrique de $A$ par rapport à $B$ alors, $B$ est milieu de $[AD]$
$E$ symétrique de $A$ par rapport à $C$ donc, $C$ est milieu de $[AE]$
Alors, d'après le théorème de la droite des milieux, la droite $(BC)$ passant par $B\ $ et $\ C$ milieux respectifs des segments $[AD]\ $ et $\ [AE]$ est parallèle à la droite $(DE).$
2) On appelle $I$ le milieu du segment $[BC].$
La droite $(AI)$ coupe $(DE)$ en $H.$
Démontrons que $I$ est le milieu du segment $[AH].$
Considérons le triangle $ADH.$
On a : la droite $(BI)$ passant par $B$ milieu de $[AD]$ est parallèle à $(DH).$
Donc, d'après la réciproque du théorème de la droite des milieux, la droite $(BI)$ coupe le segment $[AH]$ en son milieu.
Or, $(BI)\ $ et $\ [AH]$ se coupent en $I.$
Par conséquent, $I$ est le milieu du segment $[AH].$
3) Démontrons que les droites $(DC)\;,\ (AH)\ $ et $\ (BE)$ sont concourantes.
En effet, comme $[BC]\ $ et $\ [AH]$ ont même milieu $I$ alors, $ABHC$ est un parallélogramme.
Par suite, $(BH)$ est parallèle à $(AC).$
Or, $B$ est milieu de $[AD].$
Donc, en appliquant la réciproque du théorème de la droite des milieux dans le triangle $ADE$, on a : $(BH)$ coupe $[DE]$ en son milieu.
Ainsi, $H$ est milieu de $[DE].$
D'où, $(AH)$ est une médiane du triangle $ADE.$
Par ailleurs, $(DC)\ $ et $\ (AH)$ sont aussi des médianes de ce même triangle.
Or, on sait que : dans un triangle, les médianes se coupent en un point.
Par conséquent, les droites $(DC)\;,\ (AH)\ $ et $\ (BE)$ sont concourantes.

Exercice 19
Soit un parallélogramme $ABCD.$
Le point $E$ est le symétrique de $D$ par rapport à $C.$
Les droites $(AD)\ $ et $\ (BE)$ se coupent en $F.$
1) Montrons que $B$ est le milieu de $[EF].$
Considérons le triangle $DEF.$
Comme $E$ est le symétrique de $D$ par rapport à $C$ alors, $C$ est milieu de $[DE].$
Par ailleurs, $ABCD$ étant un parallélogramme alors, $(BC)$ est parallèle à $(AD).$
Ainsi, dans le triangle $DEF$, la droite $(BC)$ parallèle à $(DF)$ et passant par $C$ milieu de $[DF]$, coupe $[EF]$ en $B.$
Donc, d'après la réciproque du théorème de la droite des milieux, $B$ est le milieu de $[EF].$
2) Montrons que $A$ est le milieu de $[DF].$
En effet, comme $ABCD$ est un parallélogramme alors, $(AB)$ est parallèle à $(DC).$
Donc, en considérant le triangle $DEF$, on a : la droite $(AB)$ passant par $B$ milieu de $[EF]$ et parallèle à la droite $(DE)$, coupe $[DF]$ en $A.$
Ainsi, d'après la réciproque du théorème de la droite des milieux, $A$ est le milieu de $[DF].$
3) Les droites $(DB)\ $ et $\ (FC)$ se coupent en $G.$
Démontrons que les points $E\;,\ G\ $ et $\ A$ sont alignés.
On a : $(DB)\ $ et $\ (FC)$ sont deux médianes du triangle $DEF$ qui se coupent en $G.$
$G$ est alors le centre de gravité du triangle $DEF.$
Comme $(AE)$ passe par le sommet $E$ et par le milieu $A$ du côté opposé à ce sommet alors, $(AE)$ est la troisième médiane du triangle $DEF.$
Ce qui signifie que, $(AE)$ passe aussi par $G.$
Par conséquent, les points $E\;,\ G\ $ et $\ A$ sont alignés.

Exercice 20
1) Construisons un triangle $EFG$ rectangle en $F.$
Plaçons $K$ le milieu du segment $[EG].$
Traçons la droite passant par $K$ et perpendiculaire à $(EF).$
Elle coupe $[EF]$ en $L.$
2) Démontrons que $L$ est le milieu du segment $[EF].$
Dans le triangle $EFG$, on a : $K$ milieu de $[GF].$
De pus, on sait que : si deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.
Or, $(EF)$ perpendiculaire à $(KL)\ $ et $\ (EF)$ perpendiculaire à $(GF).$
Par conséquent, $(KL)\ $ et $\ (GF)$ sont parallèles.
Donc, en appliquant la réciproque du théorème de la droite des milieux, $L$ est le milieu de $[EF].$
3) Les droites $(FK)\ $ et $\ (GL)$ se coupent en $M.$
Les droites $(FK)\ $ et $\ (GL)$ représentent des médianes du triangle $EFG$
En effet, ces droites passent par un sommet et par le milieu du côté opposé au sommet.
Par conséquent, ce sont des médianes du triangle $EFG.$
Déduisons-en que la droite $(EM)$ coupe le segment $[FG]$ en son milieu.
En effet, on a : les deux médianes $(FK)\ $ et $\ (GL)$ se coupent en $M$ donc, $M$ est le centre de gravité du triangle $EFG.$
Comme $(AM)$ passe par le sommet $E$ et par le centre de gravité $M$ alors, $(EM)$ représente la troisième médiane du triangle $EFG.$
Or, on sait que : dans un triangle, une médiane est une droite qui passe par un sommet et qui coupe le côté opposé à ce sommet en son milieu.
D'où, la droite $(EM)$ coupe le segment $[FG]$ en son milieu.

Exercice 21
$MIL$ est un triangle, $A\;,\ B\ $ et $\ C$ les milieux respectifs des cotés $[MI]\;,\ [IL]\ $ et $\ [ML].$
Soit $G$ son centre de gravité.
1) Démontrons que le quadrilatère $MABC$ est un parallélogramme.
2) $(AC)\ $ et $\ (MB)$ se coupent en $J.$
Démontrons que $J$ est le milieu de $[AC].$
Dans le triangle$MIL$, on a : $A\;,\ B\ $ et $\ C$ milieux respectifs des côtés $[MI]\;,\ [IL]\ $ et $\ [ML].$
Donc, en appliquant le théorème de la droite des milieux, on obtient : $(BC)\parallel(AM)\ $ et $\ (AB)\parallel(MC)$
Ainsi, le quadrilatère $MABC$ a ses côtés parallèles $2$ à $2.$
Par conséquent, c'est un parallélogramme.
D'où, ses diagonales $[AC]\ $ et $\ [BM]$ se coupent en leur milieu.
Ce qui signifie que $J$ est le milieu de $[AC].$
3) Démontrons que $G$ est le centre de gravité du triangle $ABC.$
En effet, dans le triangle $ABC$, on a : $(BM)$ passe le sommet $B$ et par le milieu $J$ du côté $[AC].$ Donc, la droite $(BM)$ est une médiane.
Par ailleurs, en appliquant la même méthode que dans la question $2)$, on peut montrer que $AIBC\ $ et $\ ABLC$ sont des parallélogrammes.
Ainsi, les diagonales $(CI)\ $ et $\ (AB)$ se coupent en leur milieu. Donc, $(CI)$ passe par le sommet $C$ et par le milieu du côté $[AB].$
Par suite, la droite $(CI)$ est une médiane du triangle $ABC$
De la même manière, les diagonales $(AL)\ $ et $\ (BC)$ se coupent en leur milieu.
Donc, $(AL)$ passant par le sommet $A$, coupe $[BC]$ par le milieu.
Par conséquent, la droite $(AL)$ est une médiane du triangle $ABC$
Ainsi, on constate que ces trois médianes $(BM)\;,\ (CI)\ $ et $\ (AL)$ se coupent en $G.$
Or, dans un triangle, les trois médianes se coupent en un point appelé centre de gravité de ce triangle.
Donc, $G$ est le centre de gravité du triangle $ABC.$

Exercice 22
$PQR$ est un triangle.
1) Construisons le point $M$ milieu de $[PQ]$ et le point $K$, symétrique de $P$ par rapport à $R.$
La droite $(KM)$ coupe le segment $[RQ]$ en $I$ et la droite $(PI)$ coupe $[KQ]$ en $N.$
2) Démontrons que $N$ est le milieu du segment $[KQ].$
Considérons le triangle $PQK.$
Comme $K$ est le symétrique de $P$ par rapport à $R$ alors, $R$ est milieu de $[PK].$
Or, $M$ est le milieu de $[PQ]$
Donc, les droites $(KM)\ $ et $\ (RQ)$ sont des médianes de ce triangle.
Par ailleurs, $(KM)\ $ et $\ (RQ)$ se coupent en $I.$
Par conséquent, $I$ est le centre de gravité du triangle $PQK.$
Ainsi, $(PI)$ étant la droite passant par le sommet $P$ et par le centre de gravité $I$ alors, $(PI)$ est la troisième médiane de ce triangle.
Donc, la droite $(PI)$ coupe $[KQ]$ par le milieu.
D'où, $N$ est le milieu du segment $[KQ].$

Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
dim, 06/27/2021 - 13:51
Permalien
Merci
Ajouter un commentaire