Les nombres décimaux relatifs - 5e

Classe: 
Cinquième
 

I. Rappels

I.1. Les nombres entiers naturels

Les nombres entiers naturels sont les nombres qui nous servent à compter.
 
Exemples : 1; 2; 3;……; 100…etc
 
L'ensemble des entiers naturels se nomme N

I.2. Les nombres entiers relatifs

Les nombres entiers relatifs sont les nombres entiers naturels précédés par un signe (+) ou un signe (−).

Exemples :

−20; 0; +100
 
L'ensemble des entiers relatifs se note Z

Remarque 

Tout entier naturel est aussi un entier relatif ; c'est-à-dire
N⊂Z

I.3. Les nombres décimaux

Un nombre décimal est un nombre composé de deux parties : une partie entière (PE) et une partie décimale (PD), séparées par une virgule.

Exemples :

1634⏟PE,28⏟PD;260,20;5,3

II. Les décimaux relatifs

II.1. Définition

Les nombres décimaux relatifs sont les nombres décimaux précédés par les signes (+) ou (−)

Exemples :

−0,5;+10,4;+20
 
L'ensemble des décimaux relatifs se note D

Remarque 

Tout entier relatif est un décimal relatif. On a finalement :
N⊂Z⊂D
La partie entière comme la partie décimale d'un nombre décimal relatif peuvent être nulles.

II.2. Repérer des points sur une droite graduée par des décimaux relatifs

Sur une droite (D) donnée, on demande de :
 
1) Placer les points A  et  B
 
2) Graduer la droite (D) en prenant A comme origine et distance A−B comme unité.
 
3) Placer le point C tel que A−C égale à 2,5cm
 
4) Placer le point E tel que A soit le milieu de [E−C]
 
5) Quel est le nombre décimal associé à E ?

Solution


 

 
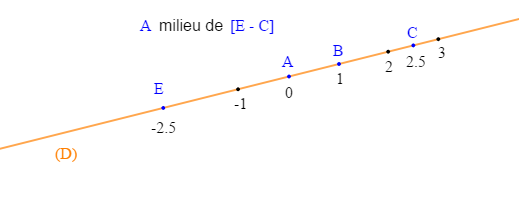
−2,5 est la valeur de E
 
Sur la droite graduée, le nombre associé à un point est appelé abscisse.

Exemples :

0 est l'abscisse du point A
 
1 est l'abscisse du point B
 
2,5 est l'abscisse du point C
 
−2,5 est l'abscisse du point E

II.3. Valeur absolue

Sur une droite graduée, la valeur absolue d'un nombre est la distance du point d'origine au point associé à ce nombre.
 
Pour le cas de l'exemple précédent :
 
AC=+2,5=|+2,5|
 
AE=2,5=|−2,5|
 
D'une manière générale, la valeur absolue du nombre a se note |a| et il est toujours plus grand que 0 ; c'est-à-dire toujours positive.

Application

Sur une droite graduée, les points E; F; G d'abscisses respectives −5; −1; +2.5
 
Placer les points E; F; G puis calculer les distances EF; FG; EG

 

 
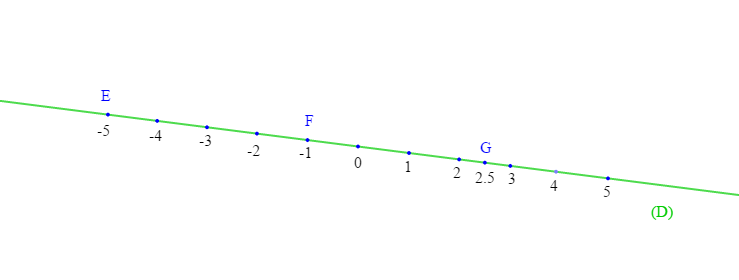
La distance EF est de : |+4|
 
La distance FG est de : |+3,5|
 
La distance EG est de : |+7,5|

III. Comparaison des nombres décimaux

III.1. Nombres décimaux de signes différents

Si deux nombres décimaux relatifs sont de signes différents, le plus grand est celui qui a le signe positif.

Exemple :

−5,2<+2,4

III.2. Nombres décimaux relatifs positifs

+5>+2 évidence
 
+1001<3005

III.3. Nombres décimaux relatifs négatifs

−10<−3
 
3<10 donc, −3 est plus grand que −10
 
Si deux décimaux relatifs sont négatifs, le plus grand est celui qui a la plus petite valeur absolue.

Exemples :

−7,5;−139,4
 
|−7,5|=+7,5  et  |−139,4|=139,4
 
7,5 étant plus petit donc, −7,5>−139,4

Remarque

De deux nombres décimaux relatifs négatifs, le plus grand est celui étant plus proche de 0.

Application

1) Ranger dans l'ordre croissant :
−102,5;+7;−15,2;0;−2;+3,4;+4,6
1) Ranger dans l'ordre décroissant :
+13;−2,7;−5,3;0;−100;+18;+46

Réponses

1) Je range dans l'ordre croissant
−102,5;−15,2;−2;0;+3,4;+4,6;+7
1) Je range dans l'ordre décroissant
+46;+18;+13;0;−2,7;−5,3;−100

Remarque

−6  et  +6 sont des nombres opposés car ils ont la même valeur absolue mais des signes contraires.
 

Auteur: 
Mamadou Siradji Dia

Commentaires

Assane sogue (non vérifié)

lun, 11/23/2020 - 21:10

C'est un bon site

Ndeye sokhna gueye (non vérifié)

lun, 07/05/2021 - 15:29

Merci beaucoup

Ndeye sokhna gueye (non vérifié)

lun, 07/05/2021 - 15:29

Merci beaucoup

Assane sogue (non vérifié)

lun, 11/23/2020 - 21:12

C'est un bon site parce qu'il me tout nécessaire

Anonyme (non vérifié)

mer, 12/30/2020 - 11:15

Bien mais pas d'exercice s

Mouhamed Bitéye (non vérifié)

mer, 05/26/2021 - 22:26

En apprenant

Mouhamed Bitéye (non vérifié)

mer, 05/26/2021 - 22:26

En apprenant

mame diarra bao (non vérifié)

ven, 06/04/2021 - 20:57

Très intéressant mais pas d'évaluation

Anonyme (non vérifié)

sam, 06/19/2021 - 14:58

POUR INFO IL Y A DES EXERCICES

Moussou Sow sy (non vérifié)

jeu, 06/24/2021 - 00:17

C'est un très bon site j'y apprends beaucoup de chose je veux être doué en math pour devenir docteur

Anonyme (non vérifié)

sam, 06/26/2021 - 17:21

C'est un très bon math

Baye Mbåckę sënē (non vérifié)

mar, 07/06/2021 - 18:00

Aucune balise HTML autorisee

Anonyme (non vérifié)

dim, 07/04/2021 - 08:32

j'apprends bien le math car je veux être un ingénieur

Anonyme (non vérifié)

lun, 07/12/2021 - 22:34

C'est vraiment intéressant

Anonyme (non vérifié)

lun, 07/26/2021 - 04:27

J'adore ce site c'est le meuilleur

maman khady sene (non vérifié)

mar, 06/14/2022 - 08:50

c trop bien la leçon

maman khady sene (non vérifié)

mar, 06/14/2022 - 08:50

c trop bien la leçon

Ajouter un commentaire