Repérage dans le plan 3e
Classe:
Troisième
I. repérage orthonormal
Soient $\vec{i}\ $ et $\ \vec{j}$ deux vecteurs du plan de direction respective $(x'x)\ $ et $\ (y'y)$ non parallèles et $O$ leur point d'intersection.
On appelle repère cartésien, le triplet $(O\;;\ \vec{i}\;,\ \vec{j}).$
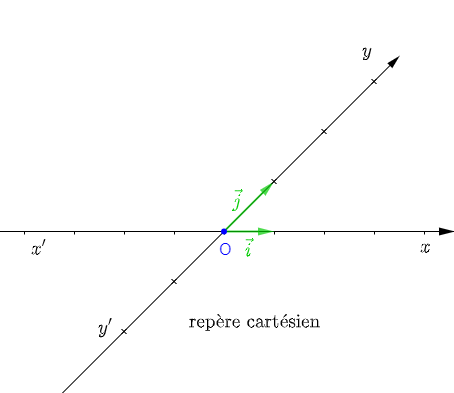
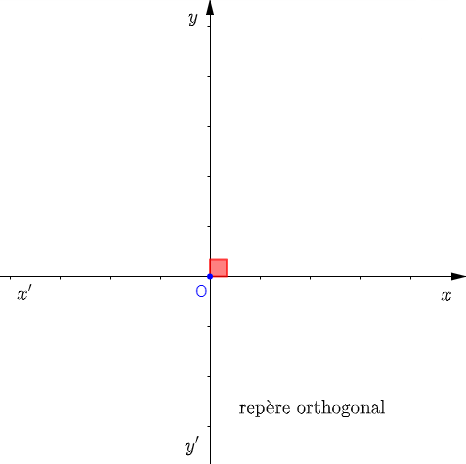
Si $(x'x)\perp(y'y)$ alors, le repère cartésien sera le repère orthogonal.
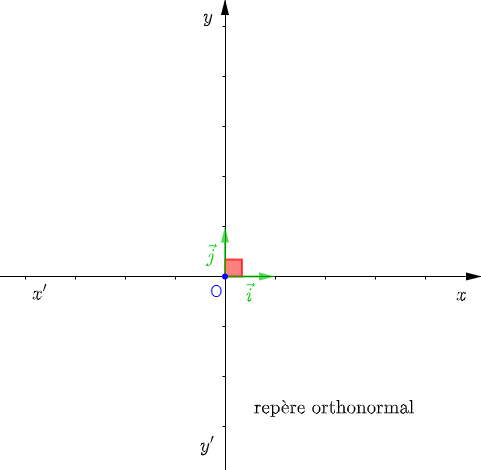
Si, pour le repère orthogonal, on a $\ell_{\vec{i}}=\ell_{\vec{j}}$ alors, le repère sera dit repère orthonormal.
Le point $O$ est appelé origine du repère et les axes $(x'x)\ $ et $\ (y'y)$sont respectivement appelés axe des abscisses et axe des ordonnées.
Remarque :
En posant $\vec{i}=\overrightarrow{OI}\ $ et $\ \vec{j}=\overrightarrow{OJ}$, le repère orthonormal sera noté $(O\;;\ I\;,\ J)$
II. Coordonnées d'un point dans un repère orthonormal
Soient $(O\;;\ I\;,\ J)$ un repère orthonormal et $M$ un point du plan.
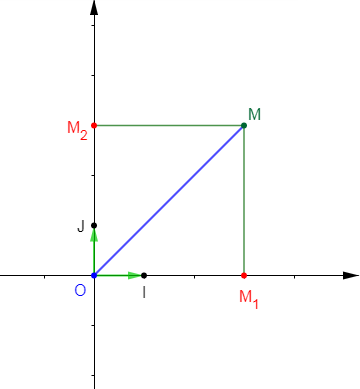
On a : $OM_{1}MM_{2}$ un parallélogramme alors, $\overrightarrow{OM}=\overrightarrow{OM_{1}}+\overrightarrow{OM_{2}}.$
Or, les vecteurs $\overrightarrow{OM_{1}}\ $ et $\ \overrightarrow{OM_{2}}$ sont respectivement colinéaires aux vecteurs $\vec{i}\ $ et $\ \vec{j}.$
Donc, il existe deux réels $x\ $ et $\ y$ tels que $\overrightarrow{OM_{1}}=x.\vec{i}\ $ et $\ \overrightarrow{OM_{2}}=y.\vec{j}.$
Ainsi, $\overrightarrow{OM}=x.\vec{i}+y.\vec{j}.$ D'où le couple $(x\;;\ y)$ est appelé les coordonnées du point $M$ dans le repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
On notera $M\begin{pmatrix} x\\ y\end{pmatrix}$ ou $M(x\;;\ y)$
Si $M$ a pour coordonnées $\begin{pmatrix} x\\ y\end{pmatrix}$ dans le repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ alors, $\overrightarrow{OM}=x.\vec{i}+y.\vec{j}.$
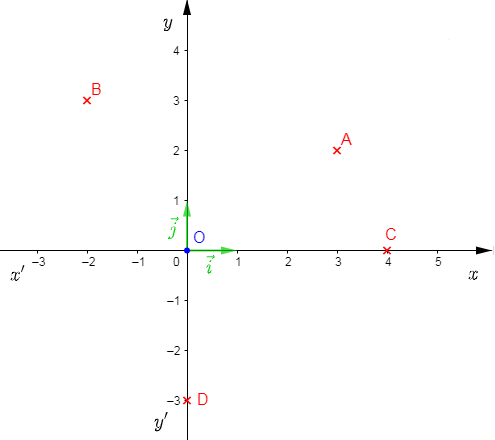
Exemple :
On considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne :
$\overrightarrow{OA}=3\vec{i}+2\vec{j}\;;\ \overrightarrow{OB}=-2\vec{i}+3\vec{j}\;;\ \overrightarrow{OC}=4\vec{i}\ $ et $\ \overrightarrow{OD}=-3\vec{j}.$
Trouvons les coordonnées des points $A\;,\ B\;,\ C\ $ et $\ D$ et plaçons les dans le repère orthonormal.
On a : $\overrightarrow{OA}=3\vec{i}+2\vec{j}$ alors, $A\begin{pmatrix} 3\\ 2\end{pmatrix}$
$\overrightarrow{OB}=-2\vec{i}+3\vec{j}$ alors, $B(-2\;;\ 3)$
$\overrightarrow{OC}=4\vec{i}$ alors, $C\begin{pmatrix} 4\\ 0\end{pmatrix}$
$\overrightarrow{OD}=-3\vec{j}$ alors, $D(0\;;\ -3)$
Les réels $x\ $ et $\ y$ sont appelés respectivement abscisse et ordonnée du point $M$ dans le repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
$\centerdot\ \ $ Le point $O$ a pour coordonnées $\begin{pmatrix} 0\\ 0 \end{pmatrix}$, on notera $O\begin{pmatrix} 0\\ 0 \end{pmatrix}$
$\centerdot\ \ $ Si un point a pour abscisse nul, il se trouvera alors dans l'axe des ordonnées.
$\centerdot\ \ $ Si un point a pour ordonnée nulle, il se trouvera alors dans l'axe des abscisses.
III. Coordonnées d'un vecteur dans un repère orthonormal
III.1 Coordonnées d'un vecteur représenté par un bipoint.
Soient $(O\;;\ \vec{i}\;,\ \vec{j})$ un repère orthonormal, $A\ $ et $\ B$ deux points de ce repère.
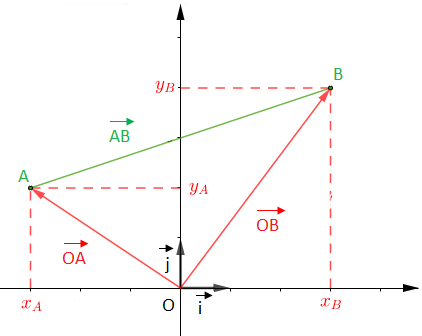
On a : $\overrightarrow{OA}=x_{A}\vec{i}+y_{A}\vec{j}\ $ et $\ \overrightarrow{OB}=x_{B}\vec{i}+y_{B}\vec{j}$
et comme $\overrightarrow{AB}=(x_{B}\vec{i}+y_{B}\vec{j})-(x_{A}\vec{i}+y_{A}\vec{j})$
alors, $\overrightarrow{AB}=x_{B}\vec{i}+y_{B}\vec{j}-x_{A}\vec{i}-y_{A}\vec{j}.$
Ainsi, $\overrightarrow{AB}=(x_{B}-x_{A})\vec{i}+(y_{B}-y_{A})\vec{j}.$
Si $A\begin{pmatrix} x_{A}\\ y_{A} \end{pmatrix}\ $ et $\ B\begin{pmatrix} x_{B} \\ y_{B}\end{pmatrix}$ dans un repère orthonormal alors, $\overrightarrow{AB}\begin{pmatrix} x_{B}-x_{A}\\ y_{B}-y_{A} \end{pmatrix}$
Exemple : on considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne :
$\overrightarrow{OA}=2\vec{i}+3\vec{j}\;;\ \overrightarrow{OB}=-3\vec{i}+2\vec{j}\ $ et $\ \overrightarrow{OC}=-\vec{i}-4\vec{j}.$
Calculons les coordonnées des vecteurs $\overrightarrow{AB}\;,\ \overrightarrow{AC}\ $ et $\ \overrightarrow{BC}$
On a : $A\begin{pmatrix} 2\\ 3 \end{pmatrix}\;,\ B\begin{pmatrix} -3\\ 2 \end{pmatrix}\ $ et $\ C\begin{pmatrix} -1\\ -4 \end{pmatrix}$
alors, $\overrightarrow{AB}\begin{pmatrix} -3-2\\ 2-3 \end{pmatrix}=\begin{pmatrix} -5\\ -1 \end{pmatrix}\;,\ \overrightarrow{AC}\begin{pmatrix} -1-2\\ -4-3 \end{pmatrix}=\begin{pmatrix} -3\\ -7\end{pmatrix}$
et $\overrightarrow{BC}\begin{pmatrix} -1-(-3)\\ -4-2\end{pmatrix}=\begin{pmatrix} 2\\ -6\end{pmatrix}$
III.2 Coordonnées d'un vecteur somme
Soient $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
On aura : $\vec{u}=x.\vec{i}+y.\vec{j}\ $ et $\ \vec{v}=x'.\vec{i}+y'.\vec{j}$
Alors, $\vec{u}+\vec{v}=(x.\vec{i}+y.\vec{j})+(x'.\vec{i}+y'.\vec{j}).$
Donc, $\vec{u}+\vec{v}=x.\vec{i}+y.\vec{j}+x'.\vec{i}+y'.\vec{j}.$
Ainsi, $\vec{u}+\vec{v}=(x+x').\vec{i}+(y+y').\vec{j}.$
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ dans un repère orthonormal alors, $\vec{u}+\vec{v}\begin{pmatrix} x+x'\\ y+y' \end{pmatrix}$
III.3 Coordonnées d'un vecteur égal à un autre
Soient $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
On se propose de trouver la condition nécessaire et suffisante pour que les vecteurs $\vec{u}\ $ et $\ \vec{v}$ soient égaux.
On a : $\vec{u}=x.\vec{i}+y.\vec{j}\ $ et $\ \vec{v}=x'.\vec{i}+y'.\vec{j}$
or, $\vec{u}=\vec{v}$
alors, $x.\vec{i}+y.\vec{j}=x'.\vec{i}+y'.\vec{j}.$
Donc, $x=x'\ $ et $\ y=y'$
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ dans un repère orthonormal et $\vec{u}=\vec{v}$ alors, $x=x'\ $ et $\ y=y'$ et réciproquement.
III.4 Coordonnées d'un vecteur opposé à un autre
Soient $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
On se propose de trouver la condition nécessaire et suffisante pour que les vecteurs $\vec{u}$ et $\vec{v}$ soient des vecteurs opposés.
On a : $\vec{u}=x.\vec{i}+y.\vec{j}$ et $\vec{v}=x'.\vec{i}+y'.\vec{j}$
or, $\vec{u}+\vec{v}=\vec{0}$
alors, $x.\vec{i}+y.\vec{j}+x'.\vec{i}+y'.\vec{j}=\vec{0}.$
Donc, $(x+x').\vec{i}+(y+y').\vec{j}=0.\vec{i}+0.\vec{j}$
Ainsi, $x+x'=0$ et $y+y'0$
d'où, $x=-x'$ et $y=-y'$
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}$ et $\vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ dans un repère orthonormal et $\vec{u}+\vec{v}=\vec{0}$ alors, $x=-x'$ et $y=-y'$ et réciproquement.
III.5 Coordonnées d'un vecteur multiplié par un réel
Soient $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}$ et $\vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs dans un repère orthonormal $(O;\ \vec{i},\ \vec{j})$ et $k\in\mathbb{R}$ tel que $\vec{v}=k.\vec{u}.$
On a : $\vec{u}=x.\vec{i}+y.\vec{j}\ $ et $\ \vec{v}=x'.\vec{i}+y'.\vec{j}$
or, $\vec{v}=k.\vec{u}.$
alors, $x'.\vec{i}+y'.\vec{j}=k(x.\vec{i}+y.\vec{j}).$
Donc, $x'.\vec{i}+y'.\vec{j}=(kx).\vec{i}+(ky).\vec{j}.$
D'où, $x'=kx$ et $y'=ky$
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}$ dans un repère orthonormal et $k\in\mathbb{R}$ alors, $k\vec{u}\begin{pmatrix} kx\\ ky \end{pmatrix}$
III.6 Condition de colinéarité de deux vecteurs
Soient $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs colinéaires dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Alors on a : $\vec{v}=k.\vec{u}$ avec $k\in\mathbb{R}.$
Donc, $x'=kx\ $ et $\ y'=ky$, par suite $\dfrac{x'}{y'}=\dfrac{kx}{ky}.$
Par conséquent, $\dfrac{x'}{y'}=\dfrac{x}{y}.$
Ainsi, $xy'=x'y$ ; d'où, $xy'-x'y=0$
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ dans un repère orthonormal et $\vec{u}\;,\ \vec{v}$ colinéaires alors, $xy'-x'y=0.$
Réciproque : Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs dans un repère orthonormal et $xy'-x'y=0$ alors, $\vec{u}\ $ et $\ \vec{u}$ colinéaires.
III.7 Applications
$\centerdot\ \ $ Coordonnées du milieu d'un segment
Soient $A\begin{pmatrix} x_{A}\\ y_{A} \end{pmatrix}\ $ et $\ B\begin{pmatrix} x_{B}\\ y_{B} \end{pmatrix}$ dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})\ $ et $\ I\begin{pmatrix} x_{I}\\ y_{I} \end{pmatrix}$ milieu de $[AB].$
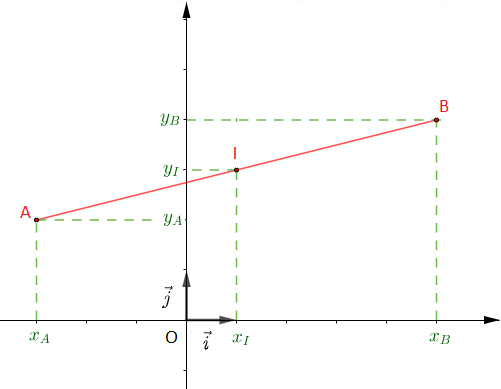
On se propose de déterminer les coordonnées du point $I$ en fonction des coordonnées des points $A\ $ et $\ B.$
On a : $I$ milieu de $[AB]$ alors, $\overrightarrow{AI}=\overrightarrow{IB}.$
Or, $\overrightarrow{AI}\begin{pmatrix} x_{I}-x_{A}\\ y_{I}-y_{A} \end{pmatrix}\ $ et $\ \overrightarrow{IB}\begin{pmatrix} x_{B}-x_{I}\\ y_{B}-y_{I} \end{pmatrix}$
Donc, $x_{I}-x_{A}=x_{B}-x_{I}$ et $y_{I}-y_{A}=y_{B}-y_{I}.$
Ainsi, $2x_{I}=x_{A}+x_{B}\ $ et $\ 2y_{I}=y_{A}+y_{B}$
D'où, $x_{I}=\dfrac{x_{A}+x_{B}}{2}\ $ et $\ y_{I}=\dfrac{y_{A}+y_{B}}{2}.$
Si $A\begin{pmatrix} x_{A}\\ y_{A} \end{pmatrix}\ $ et $\ B\begin{pmatrix} x_{B}\\ y_{B} \end{pmatrix}$ dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})\ $ et $\ I\begin{pmatrix} x_{I}\\ y_{I}\end{pmatrix}$ milieu de $[AB]$ alors, $I\begin{pmatrix} \dfrac{x_{A}+x_{B}}{2}\\ \\ \dfrac{y_{A}+y_{B}}{2} \end{pmatrix}$
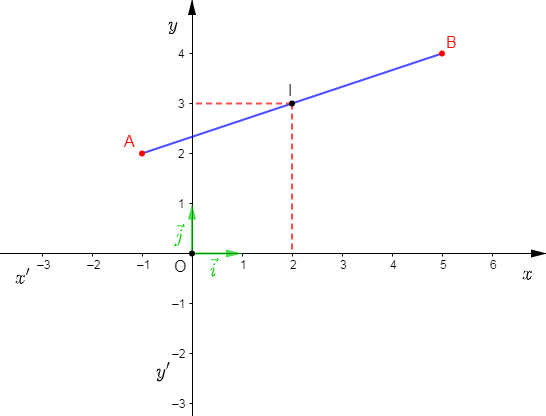
Exemple : on considère un repère orthonormal $(O;\ \vec{i},\ \vec{j})$ et on donne $A\begin{pmatrix} -1\\ 2 \end{pmatrix}\ $ et $\ B\begin{pmatrix} 5\\ 4 \end{pmatrix}.$
On a : $I$ milieu de $[AB]$ alors, $I\begin{pmatrix} \dfrac{(-1)+5}{2}\\ \\ \dfrac{2+4}{2} \end{pmatrix}$ ; donc, $I\begin{pmatrix} 2\\ 3 \end{pmatrix}.$
On considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne $A\begin{pmatrix} -1\\ 2 \end{pmatrix}\;,\ B\begin{pmatrix} 3\\ 4 \end{pmatrix}\ $ et $\ C\begin{pmatrix} 5\\ y \end{pmatrix}.$
Déterminons la valeur de $y$ pour que les points $A\;,\ B\ $ et $\ C$ soient alignés.
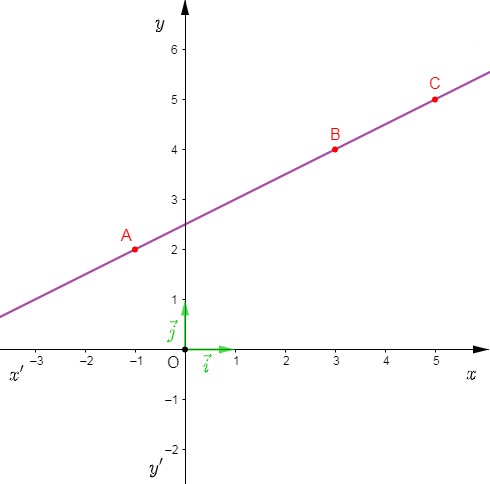
1er méthode :
On a : $A\;,\ B\ $ et $\ C$ alignés alors, $\overrightarrow{AC}=k.\overrightarrow{AB}.$
Or, $\overrightarrow{AC}\begin{pmatrix} 6\\ y-2 \end{pmatrix}\;;\ \overrightarrow{AB}\begin{pmatrix} 4\\ 2 \end{pmatrix}\ $ et $\ k.\overrightarrow{AB}\begin{pmatrix} 4k\\ 2k \end{pmatrix}$
Donc, $6=2k\ $ et $\ y-2=2k$
Ainsi, $k=\dfrac{3}{2}\ $ et $\ y-2=2\left(\dfrac{3}{2}\right)$ ; d'où, $y=5.$
2em méthode :
On a : $A\;,\ B\ $ et $\ C$ alignés alors, $\overrightarrow{AB}\ $ et $\ \overrightarrow{AB}$ colinéaires.
Or, $\overrightarrow{AB}\begin{pmatrix} 4\\ 2 \end{pmatrix}\ $ et $\ \overrightarrow{AC}\begin{pmatrix} 6\\ y-2 \end{pmatrix}$
Donc, $4(y-2)-2(6)=0$
Ainsi, $4y-8-12=0$
D'où, $y=5$
$\centerdot\ \ $ Détermination du quatrième point d'un parallélogramme
On considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne $A\begin{pmatrix} 3\\ 5 \end{pmatrix}\;,\ B\begin{pmatrix} -2\\ 2\end{pmatrix}\ $ et $\ C\begin{pmatrix} -4\\ 3\end{pmatrix}.$
Déterminons les coordonnées du point $D$ telles que $ABCD$ soit un parallélogramme.
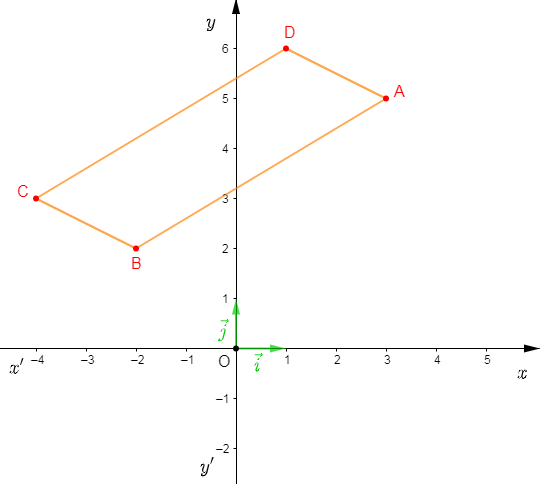
On a : $ABCD$ parallélogramme alors, $\overrightarrow{CD}=\overrightarrow{BA}.$
Or, $\overrightarrow{CD}\begin{pmatrix} x_{D}+4\\ y_{D}-3 \end{pmatrix}\ $ et $\ \overrightarrow{BA}\begin{pmatrix} 5\\ 3 \end{pmatrix}$
Donc, $x_{D}+4=5\ $ et $\ y_{D}=6$
D'où, $D\begin{pmatrix} 1\\ 6 \end{pmatrix}.$
$\centerdot\ \ $ Détermination des coordonnées du centre de gravité d'un triangle
On considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne $A\begin{pmatrix} -3\\ 3 \end{pmatrix}\;,\ B\begin{pmatrix} 6\\ 3 \end{pmatrix}\ $ et $\ C\begin{pmatrix} 3\\ 6 \end{pmatrix}.$
Déterminons les coordonnées du point $G$ centre de gravité du triangle $ABC.$
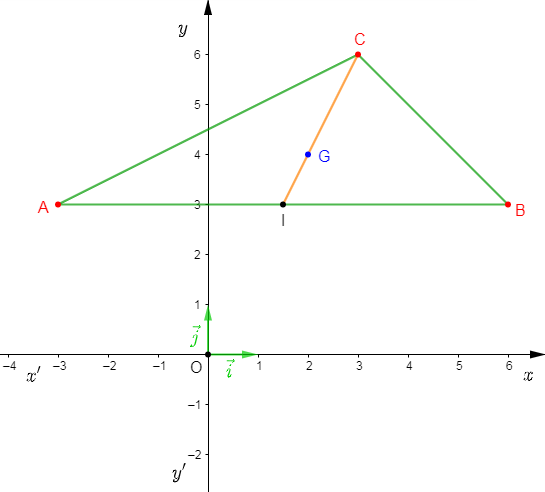
1er méthode :
On a : $G$ centre de gravité de $ABC$ alors, $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$
Or, $\overrightarrow{GA}\begin{pmatrix} -3-x_{G}\\ 3-y_{G} \end{pmatrix}\;;\ \overrightarrow{GB}\begin{pmatrix} 6-x_{G}\\ 3-y_{G} \end{pmatrix}\ $ et $\ \overrightarrow{GC}\begin{pmatrix} 3-x_{G}\\ 6-y_{G}\end{pmatrix}$
Donc, $(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC})\begin{pmatrix} 6-3x_{G}\\ 12-3y_{G} \end{pmatrix}\ $ et $\ \vec{0}\begin{pmatrix} 0\\ 0 \end{pmatrix}$
Par suite, $6-3x_{G}=0\ $ et $\ 12-3y_{G}=0$
Ainsi, $x_{G}=2\ $ et $\ y_{G}=4$
D'où, $G\begin{pmatrix} 2\\ 4 \end{pmatrix}$
2em méthode :
On a : $G$ centre de gravité de $ABC$ et $I$ milieu de $[AB].$
Alors, $\overrightarrow{IC}=3\overrightarrow{IG}$
Or, $I\begin{pmatrix} \dfrac{3}{2}\\ \\ 3 \end{pmatrix}\;,\ \overrightarrow{IC}\begin{pmatrix} \dfrac{3}{2}\\ \\ 3 \end{pmatrix}\;,\ \overrightarrow{IG}\begin{pmatrix} x_{G}-\dfrac{3}{2}\\ \\ y_{G}-3\end{pmatrix}\ $ et $\ 3\overrightarrow{IG}\begin{pmatrix} 3x_{G}-\dfrac{9}{2}\\ \\ 3y_{G}-9 \end{pmatrix}$
Donc, $\dfrac{3}{2}=3x_{G}-\dfrac{9}{2}\ $ et $\ 3=3y_{G}-9$
Ainsi, $x_{G}=2\ $ et $\ y_{G}=4$
D'où, $G\begin{pmatrix} 2\\ 4 \end{pmatrix}$
IV. Distance de deux points dans un repère orthonormal
Soient $A\begin{pmatrix} x_{A}\\ y_{A} \end{pmatrix}\ $ et $\ B\begin{pmatrix} x_{B}\\ y_{B} \end{pmatrix}$ deux points dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$
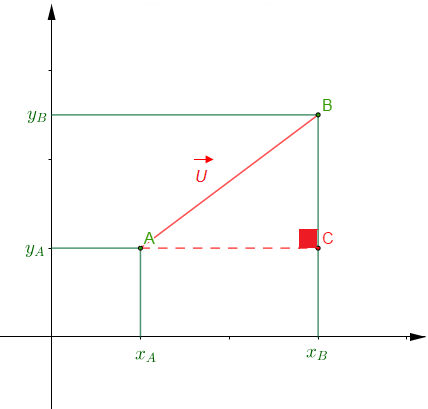
On a : $ABC$ un triangle rectangle en $C$. D'après le théorème de Pythagore, on aura : $AB=\sqrt{AC^{2}+CB^{2}}$
Or, $AC^{2}=(x_{B}-x_{A})^{2}\ $ et $\ CB^{2}=(y_{B}-y_{A})^{2}$
Donc, $AB=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}$
Si $A\begin{pmatrix} x_{A}\\ y_{A} \end{pmatrix}\ $ et $\ B\begin{pmatrix} x_{B}\\ y_{B} \end{pmatrix}$ sont deux points dans un repère orthonormal alors, $AB=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}.$
En posant $\overrightarrow{AB}=\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}$ alors, $x_{B}-x_{A}=x\ $ et $\ y_{B}-y_{A}=y$
Donc, $L_{\vec{u}}=AB=\sqrt{x^{2}+y^{2}}$
Si $\overrightarrow{AB}\begin{pmatrix} x\\ y \end{pmatrix}$ dans un repère orthonormal alors, $AB=\sqrt{x^{2}+y^{2}}.$
Applications :
$\centerdot\ \ $ Nature d'un triangle
On considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne $A\begin{pmatrix} 1\\ -2 \end{pmatrix}\;,\ B\begin{pmatrix} 2\\ 1 \end{pmatrix}\ $ et $\ C\begin{pmatrix} 5\\ 0 \end{pmatrix}.$
Déterminons la nature exacte du triangle $ABC$
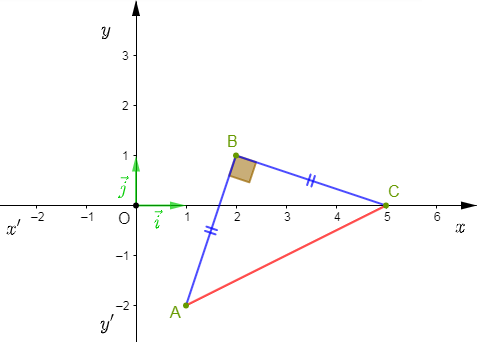
On a : $\overrightarrow{AB}\begin{pmatrix} 1\\ 3 \end{pmatrix}$ alors, $AB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$
$\overrightarrow{AC}\begin{pmatrix} 4\\ 2 \end{pmatrix}$ alors, $AC=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$
et $\overrightarrow{BC}\begin{pmatrix} 3\\ -1 \end{pmatrix}$ alors, $BC=\sqrt{3^{2}+(-1)^{2}}=\sqrt{10}$
Donc, $AB=BC.$ Ainsi, $ABC$ est un triangle isocèle en $B.$
De plus on a $AC^{2}=(2\sqrt{5})^{2}=20\;,\ AB^{2}=(\sqrt{10})^{2}=10\ $ et $\ BC^{2}=(\sqrt{10})^{2}=10.$
Par suite, $AC^{2}=AB^{2}+BC^{2}.$ D'après la réciproque du théorème de Pythagore $ABC$ est un triangle rectangle en $B.$
D'où, $ABC$ est rectangle et isocèle en $B$.
$\centerdot\ \ $ Condition d'orthogonalité de deux vecteurs dans un repère orthonormal
Soient $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ deux vecteurs dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ tels que $\vec{u}\perp\vec{v}$
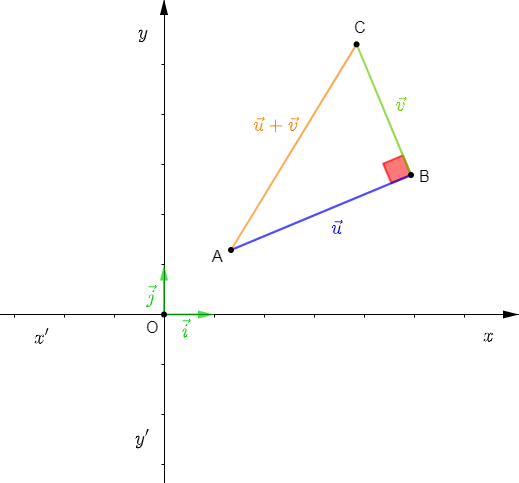
On a : $ABC$ triangle rectangle en $B$. D'après le théorème de Pythagore on aura : $AC^{2}=AB^{2}+BC^{2}.$
Or, $\overrightarrow{AC}=\vec{u}+\vec{v}\begin{pmatrix} x+x'\\ y+y' \end{pmatrix}$ alors, $AC^{2}=(x+x')^{2}+(y+y')^{2}$
$\overrightarrow{AB}=\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}$ alors, $AB^{2}=x^{2}+y^{2}$
et $\overrightarrow{BC}=\vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ alors, $BC^{2}=x'^{2}+y'^{2}$
Donc, $x^{2}+2xx'+x'^{2}+y^{2}+2yy'+y'^{2}=x^{2}+y^{2}+x'^{2}+y'^{2}$
Ainsi, $2xx'+2yy'=0$
D'où, $xx'+yy'=0$
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ sont deux vecteurs dans un repère orthonormal et $\vec{u}\perp\vec{v}$ alors, $x.x'+y.y'=0$
Réciproque :
Si $\vec{u}\begin{pmatrix} x\\ y \end{pmatrix}\ $ et $\ \vec{v}\begin{pmatrix} x'\\ y' \end{pmatrix}$ sont deux vecteurs dans un repère orthonormal tels que $x.x'+y.y'=0$ alors, $\vec{u}\perp\vec{v}$
Exemple : on considère un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et on donne $A\begin{pmatrix} 1\\ 2 \end{pmatrix}\;,\ B\begin{pmatrix} 2\\ 1 \end{pmatrix}\ $ et $\ C\begin{pmatrix} 5\\ 0\end{pmatrix}.$
Démontrons que $(AB)\perp(BC)$.
On a : $(AB)\perp(BC)$ si, et seulement si, $\overrightarrow{AB}\perp\overrightarrow{BC}.$
Or, $\overrightarrow{AB}\begin{pmatrix} 1\\ 3 \end{pmatrix}\ $ et $\ \overrightarrow{BC}\begin{pmatrix} 3\\ -1 \end{pmatrix}$ alors, $(1)(3)+(3)(-1)=3-3=0.$
Donc, $\overrightarrow{AB}\perp\overrightarrow{BC}.$
D'où, $(AB)\perp(BC)$.
V. Équation générale d'une droite
V.1 Droite passant par deux points dans un repère orthonormal
Soient $A\begin{pmatrix} -1\\ 2 \end{pmatrix}\ $ et $\ B\begin{pmatrix} 2\\ 1 \end{pmatrix}$ deux points dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminer l'équation de la droite $(AB).$
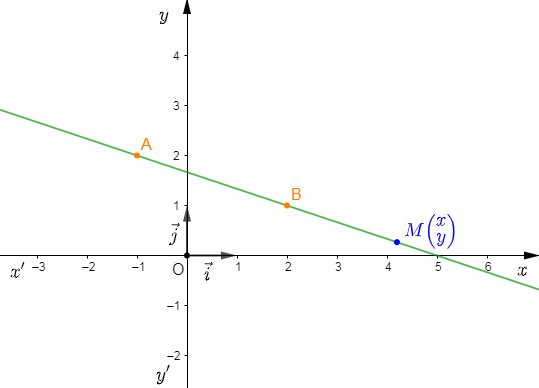
Soit $M\begin{pmatrix} x\\ y \end{pmatrix}\in\;(AB)$ alors, $\overrightarrow{AM}\ $ et $\ \overrightarrow{AB}$ sont colinéaires.
Or, $\overrightarrow{AM}\begin{pmatrix} x+1\\ y-2 \end{pmatrix}\ $ et $\ \overrightarrow{AB}\begin{pmatrix} 3\\ -1 \end{pmatrix}$
Donc, $-1(x+1)-3(y-2)=0$
Ainsi, $-x-1-3y+5=0$
D'où, $(AB)\;:\ -x-3y+5=0$ ou encore $(AB)\;:\ x+3y-5=0$
V.2 Droite définie par un vecteur et un point : vecteur directeur
Soient $\vec{u}\begin{pmatrix} 2\\ 3 \end{pmatrix}$ un vecteur et $A\begin{pmatrix} 3\\ -2 \end{pmatrix}$ un point dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminons l'équation de la droite $(\Delta)$ passant par $A$ et de direction $\vec{u}.$
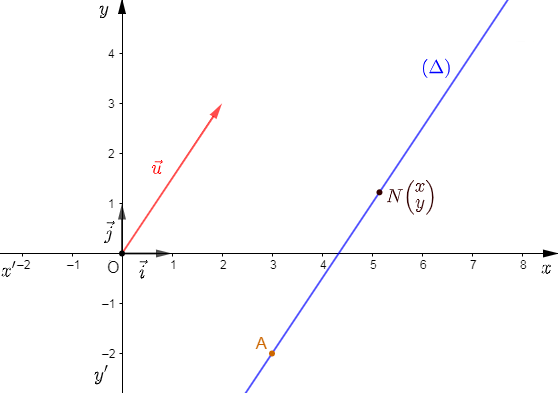
Soit $N\begin{pmatrix} x\\ y \end{pmatrix}\in\;(\Delta)$ alors, $\overrightarrow{AN}\ $ et $\ \vec{u}$ sont colinéaires.
Or, $\overrightarrow{AN}\begin{pmatrix} x-3\\ y+2 \end{pmatrix}\ $ et $\ \vec{u}\begin{pmatrix} 2\\ 3 \end{pmatrix}$
Donc, $3(x-3)-2(y+2)=0$
Ainsi, $3x-9-2y-4=0$
D'où, $(\Delta)\;:\ 3x-2y-13=0$
Le vecteur $\vec{u}$ de coordonnées $\begin{pmatrix} 2\\ 3 \end{pmatrix}$ est appelé un vecteur directeur de la droite $(\Delta)$ d'équation $3x-2y-13=0.$
Et l'équation $3x-2y-13=0$ est une équation générale de $(\Delta).$
Théorème :
Si $(\Delta)\;:\ ax+by+c=0$ alors, $\vec{u}\begin{pmatrix} -b\\ a \end{pmatrix}$ est un vecteur directeur de $(\Delta)$
Exemple : trouvons un vecteur directeur de chacune des deux droites suivantes : $(D)\;:\ 4x-3y+5=0\ $ et $\ (\Delta)\;:\ 7x+5y-13=0.$
On a : $\vec{u}\begin{pmatrix} 3\\ 4 \end{pmatrix}$ est un vecteur directeur de $(D)\ $ et $\ \vec{v}\begin{pmatrix} -5\\ 7 \end{pmatrix}$ celui de $(\Delta)$
Applications :
$\centerdot\ \ $ Droite passant par un point et parallèle à une droite donnée
Soient $(D)\;:\ 4x-3y+1=0\ $ et $\ A\begin{pmatrix} 1\\ 2 \end{pmatrix}$ un point dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminons l'équation de la droite $(\Delta)$ passant par le point $A$ et parallèle à la droite $(D).$
Soit $M\begin{pmatrix} x\\ y \end{pmatrix}\in\;(\Delta)$
On a :$(D)\;:\ 4x-3y+1=0$ et alors, $\vec{u}\begin{pmatrix} 3\\ 4 \end{pmatrix}$ un vecteur directeur.
Donc, $\overrightarrow{AM}\ $ et $\ \vec{u}$ sont colinéaires.
Or, $\overrightarrow{AM}\begin{pmatrix} x-1\\ y-2 \end{pmatrix}\ $ et $\ \vec{u}\begin{pmatrix} 3\\ 4 \end{pmatrix}$
Par suite, $4(x-1)-3(y-2)=0$
Ainsi, $4x-4-3y+6=0$
D'où, $(\Delta)\;:\ 4x-3y+2=0$
$\centerdot\ \ $ Droite passant par un point et perpendiculaire à une droite donnée
Soit $(D)\;:\ 3x+2y-5=0$ une droite données et $A\begin{pmatrix} -2\\ -3 \end{pmatrix}$ un point dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminons l'équation de la droite $(\Delta)$ passant par le point $A$ et perpendiculaire à la droite $(D).$
Soit $M\begin{pmatrix} x\\ y \end{pmatrix}\in\;(\Delta)$
On a : $(D)\;:\ 3x+2y-5=0$ et alors, $\vec{u}\begin{pmatrix} -2\\ 3 \end{pmatrix}$ un vecteur directeur.
Et comme $(\Delta)\perp D$ donc, $\overrightarrow{AM}\perp\vec{u}.$
Or, $\overrightarrow{AM}\begin{pmatrix} x+2\\ y+3 \end{pmatrix}\ $ et $\ \vec{u}\begin{pmatrix} -2\\ 3 \end{pmatrix}$
Par suite, $-2(x+2)+3(y+3)=0$
Ainsi, $-2x-4+3y+9=0$
D'où, $(\Delta)\;:\ -2x+3y+5=0$
$\centerdot\ \ $ Équation d'une droite passant par un point et parallèle à l'axe des abscisses $(xx')\;:\ y=0$
Soit $A\begin{pmatrix} a\\ b \end{pmatrix}$ un point dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminons l'équation de la droite $(\Delta)$ passant par le point $A$ et parallèle à l'axe des abscisses.
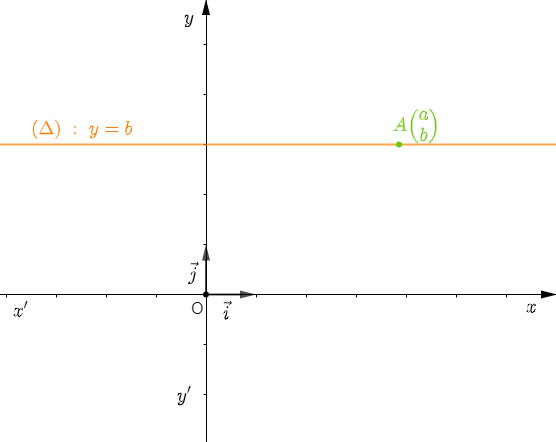
Soit $M\begin{pmatrix} x\\ y \end{pmatrix}\in\;(\Delta)$
On a : $\vec{i}\begin{pmatrix} 1\\ 0 \end{pmatrix}$ un vecteur directeur de $(xx')$ et comme $(\Delta)\parallel(xx')$ alors, $\overrightarrow{AM}$ et $\vec{i}$ sont colinéaires.
Or, $\overrightarrow{AM}\begin{pmatrix} x-a\\ y-b \end{pmatrix}\ $ et $\ \vec{i}\begin{pmatrix} 1\\ 0 \end{pmatrix}$ donc, $0(x-a)-1(y-b)=0.$
Par suite, $-y+b=0.$
D'où, $(\Delta)\;:\ y=b.$
Si $A\begin{pmatrix} a\\ b \end{pmatrix}\in\;(\Delta)$ un point dans un repère orthonormal et $(\Delta)\parallel(xx')$ alors, $(\Delta)\;:\ y=b$
$\centerdot\ \ $ Équation d'une droite passant par un point et parallèle à l'axe des ordonnées $(yy')\;:\ x=0$
Soit $A\begin{pmatrix} a\\ b \end{pmatrix}$ un point dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminons l'équation de la droite $(\Delta)$ passant par le point $A$ et parallèle à l'axe des ordonnés.
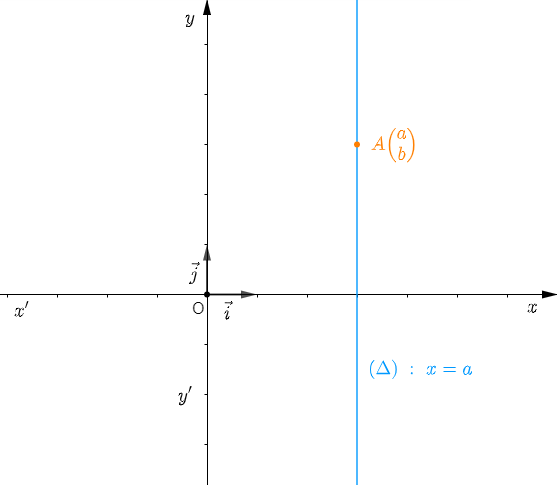
Soit $M\begin{pmatrix} x\\ y \end{pmatrix}\in\;(\Delta)$
On a : $\vec{j}\begin{pmatrix} 0\\ 1 \end{pmatrix}$ un vecteur directeur de $(yy')$ et comme $(\Delta)\parallel(yy')$ alors, $\overrightarrow{AM}\ $ et $\ \vec{j}$ sont colinéaires.
Or, $\overrightarrow{AM}\begin{pmatrix} x-a\\ y-b \end{pmatrix}\ $ et $\ \vec{j}\begin{pmatrix} 0\\ 1 \end{pmatrix}$ donc, $1(x-a)-0(y-b)=0.$
Ainsi, $x-a=0.$
D'où, $(\Delta)\;:\ x=a.$
Si $A\begin{pmatrix} a\\ b \end{pmatrix}\in\;(\Delta)$ un point dans un repère orthonormal et $(\Delta)\parallel(yy')$ alors, $(\Delta)\;:\ x=a.$
VI. Équation réduite d'une droite
VI.1 Exemples et Définitions
Soit $(\Delta)\;:\ 3x-2y+6=0$
On peut écrire alors $(\Delta)\;:\ y=\dfrac{3}{2}x+3.$
L'équation écrite sous la forme $y=\dfrac{3}{2}x+3$ est appelée équation réduite de la droite $(\Delta)$ de coefficient directeur $\dfrac{3}{2}$ et d'ordonnée à l'origine $+3.$
Ce qui signifie que la droite $(\Delta)$ passe par le point de coordonnées $(0\;;\ 3).$
De manière générale, l'équation réduite d'une droite $(\Delta)$ s'écrit sous la forme $y=ax+b$ où $a\in\mathbb{R}\ $ et $\ b\in\mathbb{R}.$
Le réel $a$ est appelé le coefficient directeur (pente) de la droite $(\Delta)$ et le réel $b$ son ordonnée à l'origine ; c'est à dire la droite passe par un point de coordonnées $(0\;;\ b).$
VI.2 Relation entre coefficient directeur et les coordonnées du vecteur directeur d'une droite
Soit $(\Delta)\;:\ 3x-2y+6=0$
On a : $\vec{u}\begin{pmatrix} 2\\ 3 \end{pmatrix}$ un vecteur directeur de $(\Delta)\ $ et $\ (\Delta)\;:\ y=\dfrac{3}{2}x+3.$
Ainsi, le coefficient directeur d'une droite est égal au rapport de l'ordonnée du vecteur directeur par son abscisse.
Si $\vec{u}\begin{pmatrix} m\\ n \end{pmatrix}$ un vecteur directeur de $(\Delta)\;:\ y=ax+b$ avec $m\neq 0$ alors, $a=\dfrac{n}{m}$
Exemple 1 : trouvons le coefficient directeur d'une droite $(\Delta)$ de vecteur directeur $\vec{u}\begin{pmatrix} -3\\ 6 \end{pmatrix}$
Soit $(\Delta)\;:\ y=ax+b\ $ et $\ \vec{u}\begin{pmatrix} -3\\ 6 \end{pmatrix}$ un vecteur directeur de $(\Delta)$ alors, $a=\dfrac{6}{-3}=-2$
Exemple 2 : trouvons un vecteur directeur de la droite $(\Delta)$ d'équation $y=\dfrac{4}{5}x-6$
On a : $\vec{u}\begin{pmatrix} 5\\ 4 \end{pmatrix}$ un vecteur directeur de $(\Delta)$.
VI.3 Propriétés
$\centerdot\ \ $ Condition de parallélisme de deux droites
Soient $(D)\;:\ y=ax+b\ $ et $\ (\Delta)\;:\ y=a'x+b'$ deux droites dans un repère orthonormal telles que $(D)\parallel(\Delta).$
On a : $\vec{u}\begin{pmatrix} 1\\ a \end{pmatrix}$ un vecteur directeur de $(D)\;,\ \vec{v}\begin{pmatrix} 1\\ a' \end{pmatrix}$ un vecteur directeur de $(\Delta)\ $ et $\ (D)\parallel(\Delta)$
alors, $\vec{u}\ $ et $\ \vec{v}$ sont colinéaires.
Donc, $1(a')-1(a)=0$
Ainsi, $a'-a=0$. D'où $a'=a$
Si $(D)\;:\ y=ax+b\ $ et $\ (\Delta)\;:\ y=a'x+b'$ deux droites dans un repère orthonormal et $(D)\parallel(\Delta)$ alors, $a=a'$
Réciproque :
Si $(D)\;:\ y=ax+b\ $ et $\ (\Delta)\;:\ y=a'x+b'$ deux droites dans un repère orthonormal et $a=a'$ alors, $(D)\parallel(\Delta)$
$\centerdot\ \ $ Condition d'orthogonalité de deux vecteurs
Soient $(D)\;:\ y=ax+b$ et $(\Delta)\;:\ y=a'x+b'$ deux droites dans un repère orthonormal telles que $(D)\perp(\Delta).$
On a : $\vec{u}\begin{pmatrix} 1\\ a \end{pmatrix}$ un vecteur directeur de $(D)\ $ et $\ \vec{v}\begin{pmatrix} 1\\ a' \end{pmatrix}$ un vecteur directeur de $(\Delta).$
Et comme $(D)\perp(\Delta)$ alors, $\vec{u}\perp\vec{v}.$
Donc, $(1)(1)+(a)(a')=0$
Ainsi, $1+a.a'=0$. D'où, $aa'=-1$
Si $(D)\;:\ y=ax+b$ et $(\Delta)\;:\ y=a'x+b'$ deux droites dans un repère orthonormal et $(D)\perp(\Delta)$ alors, $aa'=-1$
Réciproque :
Si $(D)\;:\ y=ax+b\ $ et $\ (\Delta)\;:\ y=a'x+b'$ deux droites dans un repère orthonormal et $aa'=-1$ alors, $(D)\perp(\Delta)$
Applications :
$\centerdot\ \ $ Droite passant par deux points dans un repère orthonormal
Soit $A\begin{pmatrix} -1\\ 2 \end{pmatrix}\ $ et $\ B\begin{pmatrix} 2\\ 1 \end{pmatrix}$ deux points dans un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j}).$
Déterminons l'équation de la droite $(AB)$
Soit $(AB)\;:\ y=ax+b$. On a $\overrightarrow{AB}\begin{pmatrix} 3\\ -1 \end{pmatrix}$ un vecteur directeur de $(AB)$ alors, $a=-\dfrac{1}{3}$
Donc, $(AB)\;:\ y=-\dfrac{1}{3}x+b$ et $A\begin{pmatrix} -1\\ 2 \end{pmatrix}\in\;(AB)$
Par suite, $2=-\dfrac{1}{3}(-1)+b$
Ainsi, $b=2-\dfrac{1}{3}=\dfrac{5}{3}$
D'où, $(AB)\;:\ y=-\dfrac{1}{3}x+\dfrac{5}{3}$
Auteur:
Abdoulaye Ba

Commentaires
Mory (non vérifié)
mer, 11/27/2019 - 19:26
Permalien
Contribution
Anonyme (non vérifié)
dim, 08/16/2020 - 18:33
Permalien
J'aurais voulu savoir comment
Niang (non vérifié)
dim, 08/16/2020 - 18:34
Permalien
J'aurais voulu savoir comment
yahya (non vérifié)
mer, 04/22/2020 - 23:24
Permalien
pc
Anonyme (non vérifié)
sam, 08/07/2021 - 18:23
Permalien
Vrmt ça m'a beaucoup aide
Ibrahima Diouf (non vérifié)
mar, 11/02/2021 - 23:24
Permalien
Bien
Anonyme (non vérifié)
mar, 05/07/2024 - 20:29
Permalien
c'est cool
Anonyme (non vérifié)
mer, 09/11/2024 - 13:54
Permalien
merci
Anonyme (non vérifié)
ven, 04/11/2025 - 00:09
Permalien
Excellent cours trés bien
Ajouter un commentaire