Énergie potentielle-énergie mécanique - 1er s
Classe:
Première
Le comportement prévisible d'un système dépend des valeurs de certains paramètres dites variable d'état mesurés sur le système et caractérisant l'état du système. Les énergies faisant intervenir un paramètre de position sont dites Énergies potentielles.
I. Énergie potentielle
1. Généralités
On dit qu'un système possède de l'énergie lorsqu'il est capable de produire du mouvement. Si un corps est animé d'une certaine vitesse il possède alors de l'énergie cinétique. Même un corps immobile peut fournir un travail
Exemples :
ressort tendu, retenue d'eau dans un barrage, arc tendu.
L'énergie potentielle par ces corps dépend de la position relative des différents points du système.
2. Définition
L'énergie potentielle d'un système est l'énergie qu'il peut libérer en modifiant les positions relatives des diverses parties en interaction.
3. Énergie potentielle de la pesanteur
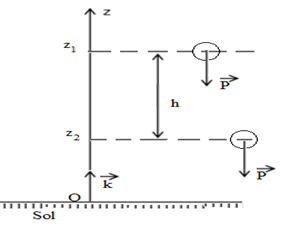
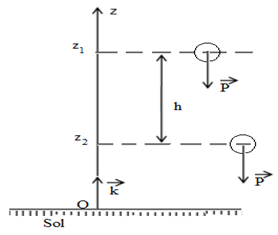
Considérons le système « Bille-Terre »
$W_{\overrightarrow{P}}=mgh$ or $h=z_{1}-z_{2}\Rightarrow W_{\overrightarrow{P}}=mg\left(z_{1}-z_{2}\right)$
$W_{\overrightarrow{P}}=mgz_{1}-mgz_{2}$
En posant $E_{P_{1}}=mgz_{1}$ et $E_{P_{2}}=mgz_{2}$
$E_{P}$ est appelée l'énergie potentielle de pesanteur. L'énergie potentielle d'un solide est l'énergie qu'il possède du fait de sa position par rapport à la Terre. A partir de l'inégalité $E_{p_{1}}-E_{p_{2}}= mgz_{1}-mgz_{2}$, il est possible de choisir pour $E_{p}$ de l'expression.
$E_{p}=mgz$
Mais on peut remarquer que l'inégalité précédente reste vérifiée si l'on ajoute à $mgz$ une constante arbitraire. L'expression générale est donc $E_{p}=mgz+cte$
$E_{p}=$ Énergie potentielle de la pesanteur
$m$ : masse du corps
$z$ : altitude ou (cote)
L'énergie potentielle de pesanteur n'est définie qu'a une constante arbitraire prés. Seules les variations sont définies.
3.1. Unités
Comme est l'opposé d'un travail. L'énergie potentielle d'une pesanteur s'exprime avec la même unité que le travail, c'est-à-dire en Joules $(J)$
3.2. État de référence
L'énergie potentielle d'un corps est définie à une constante additive prés qui dépend de l'état de référence. On convient souvent de choisir la valeur nulle ou lu l'énergie potentielle de position $E_{p}$ $(z_{réf})=0.$
Le choix d'une position de référence conduit à fixer une valeur ou la constante arbitraire (Cte), donc à lever l'indétermination de l'expression $E_{p}.$
En effet l'expression
\begin{eqnarray} E_{p}\left(z_{\text{réf}}\right) &=& mgz_{\text{réf}}+\text{Cte}\nonumber\\\\ &=&0\nonumber\\\\\Rightarrow \text{Cte} &=&-mgz_{\text{réf}}\nonumber\\\\\Rightarrow E_{p}(z) &=&mg\left(z-z_{\text{réf}}\right) \end{eqnarray}
Conséquences
$\blacktriangleright\ $Si $z<z_{\text{réf}}\Rightarrow\;E_{p}<0$
$\blacktriangleright\ $Si $z>z_{\text{réf}}\Rightarrow\;E_{p}>0$
Cas particulier
$\blacktriangleright\ $Si $<z_{\text{réf}}=0\Rightarrow\;E_{p}(z)=mgz$
Si la position de référence correspond à l'énergie des cotes (altitudes). $E_{p}$ prend son expression le plus simple $(mgz)$
3.2. Variation de l'énergie potentielle de pesanteur
\begin{eqnarray} W_{\overrightarrow{P}} &=&mgh\quad\text{or }\nonumber\\\\ h&=&z_{1}-z_{2}\nonumber\\\\\Rightarrow W_{\overrightarrow{P}} &=&mg\left(z_{1}-z_{2}\right)\nonumber\\\\\Rightarrow W_{\overrightarrow{P}} &=& E_{P_{1}}-E_{P_{2}}\nonumber\\\\ &=&-\left(E_{P_{2}}-E_{P_{1}}\right) \end{eqnarray}
En posant $E_{P_{1}}=mgz_{1}$ et $E_{P_{2}}=mgz_{2}$
$\Delta E_{P}=-W_{\overrightarrow{P}}$

La variation de l'énergie potentielle de pesanteur est à l'opposé du travail du poids d'un corps.
4. Énergie potentielle plastique
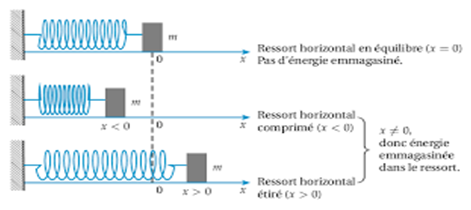
Considérons le système « masse-ressort »
Lorsque l'extrémité libre d'un ressort est déplacée par rapport à la position d'équilibre d'une abscisse $x$, le ressort possède potentielle élastique :
$E_{p}=\dfrac{1}{2}kx^{2}+$cte avec $k$ la constante de raideur en $N\cdot m^{-1}$ ;
$E_{p}$ en joules $(J)$

Cas particulier
Si cte$=0$ alors $E_{p}$ prend une valeur particulière
$$E_{p}=\dfrac{1}{2}kx^{2}$$
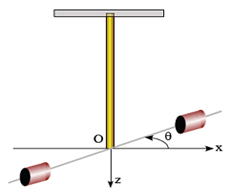
5. Énergie potentielle de torsion
Lorsque le fil est déformé par une tension élastique d'un angle $\theta$ il acquiert une énergie potentielle de torsion tel que :
$E_{p}=\dfrac{1}{2}C\theta^{2}+$cte avec $C$ : la constante de torsion en $N\cdot m\cdot rad^{-1}$ ;
$E_{p}$ en joules $(J).$
Si cte$=0\Rightarrow\;E_{p}=\dfrac{1}{2}C\theta^{2}$

6. Généralisation
6.1. Variation de l'énergie potentielle
La variation de l'énergie potentielle d'un système entre deux instants donnés est opposée au travail des forces extérieures.
6.2. Formes conservatives
Une force est dite conservative si son travail ne dépend pas du chemin suivi mais de la position initiale et de la position finale de son point d'application.
Exemple de forces conservatives :
les forces électrostatiques, les forces de gravitations (poids d'un corps), les forces élastiques (ressort, pendule de torsion) les rections normales.
II. Énergie Mécanique
1. Définition
Lors de la chute d'un corps de masse $(m)$, la variation de l'énergie cinétique est égale au travail du poids.
\begin{eqnarray} E_{c_{2}}-E_{c_{1}}&=&W_{\overrightarrow{P}}\nonumber\\\\\text{or }W_{\overrightarrow{P}}&=&-\Delta E_{p}\nonumber\\\\\Rightarrow E_{c_{2}}-E_{c_{1}}&=&-\left(E_{p_{2}}-E_{p_{1}}\right)\nonumber\\\\\Rightarrow E_{c_{2}}+E_{c_{1}}&=&E_{c_{1}}+E_{p_{1}} \end{eqnarray}
On constate qu'au cours de la transformation la somme de l'énergie cinétique et de l'énergie potentielle est constante. On appelle l'énergie mécanique d'un système à chaque instant dans un repère donné la somme des énergies cinétique et potentielle
$$E_{m}=E_{c}+E_{p}$$
2. Conservation de l'énergie mécanique
2.1. Loi de conservation
Soit un système se déplaçant d'une position $1$ en une position $2$ en étant soumis à des forces conservatives uniquement de résultante $F.$
Appliquons le théorème de l'énergie cinétique entre $1$ et $2$
\begin{eqnarray} E_{c_{2}}-E_{c_{1}}&=&W_{\overrightarrow{F}}\nonumber\\\\\text{or }W_{\overrightarrow{F}}&=&-\Delta E_{p}\nonumber\\\\\Rightarrow E_{c_{2}}-E_{c_{1}}&=&-\left(E_{p_{2}}-E_{p_{1}}\right)\nonumber\\\\\Rightarrow E_{c_{2}}+E_{p_{2}}&=&E_{c_{1}}+E_{p_{1}}\nonumber\\\\\Rightarrow E_{m_{2}}&=&E_{m_{1}} \end{eqnarray}
Ce résultat est indépendant des positions $1$ et $2$ choisies
Conclusion
L'énergie mécanique d'un système soumis à des forces conservatives est constante.
2.2. Autre formulation
La loi de conservation de l'énergie mécanique se traduit au cours du déplacement par une transformation de l'énergie potentielle en énergie cinétique ou inversement.
3. Théorème de l'énergie mécanique
Soit un système qui se déplace d'une position 1 à une autre $2.$ Sur ce système s'appliquent les forces conservatives de résultante $\overrightarrow{F}$ et les forces non conservatives de résultante $\overrightarrow{f}.$
Le théorème de l'énergie cinétique donne :
\begin{eqnarray} \Delta E_{C}&=&W_{\overrightarrow{F}}+W_{\overrightarrow{f}}\quad\text{or }\nonumber\\\\ W_{\overrightarrow{F}}&=-\Delta E_{P}\nonumber\\\\\Rightarrow \Delta E_{C} &=& E_{P_{1}}-E_{P_{2}}+W_{\overrightarrow{f}} \nonumber\\\\\Rightarrow E_{C_{2}}+E_{P_{2}}-\left(E_{C_{1}}+E_{P_{1}}\right)\nonumber\\\\\Rightarrow E_{m_{2}}-E_{m_{1}}&=&W_{\overrightarrow{f}}\nonumber\\\\\Rightarrow\Delta E_{m}&=&W_{\overrightarrow{f}} \end{eqnarray}
Conclusion
La variation de l'énergie mécanique d'un système entre deux instants données est égale la somme des travaux des forces non conservatives entre ces $2$ instants ou $f$ est la résultante des forces non conservatives.
$$\Delta E_{m}=W_{\overrightarrow{f}}$$
Exercice d'application
Un jouet d'une gouttière $ABC$ comportant $2$ parties : $AB$ est horizontale, $BC$ est un arc de cercle de centre $O$ de rayon $R.$ la gouttière se trouve dans un plan vertical. $OB$ se trouvant sur le même vertical.
Un solide de masse $m$ poids peut être lancé par l'intermédiaire d'un ressort de raideur $K$
1. Trouvons la diminution minimale de longueur $l_{0}$ qu'il faut exprimer pour qu'il puisse envoyer le solide jusqu'au $C.$ on néglige les forces de frottements.
On donne :
$m=100g$, $R=0.50m$, $\alpha=60^{\circ}$, $K=10N\cdot m^{-1}$ et $g=10$ SI
2. On imprime maintenant au ressort une diminution de longueur à $2l_{0}.$
Trouver la vitesse du solide au passe par le point $C.$
Résolution
1. La diminution minimale $l_{0}$
Système étudié :
Autre méthode

Commentaires
Anonyme (non vérifié)
mer, 06/23/2021 - 21:15
Permalien
La leçon n'est pas termine
fcherif
mer, 06/23/2021 - 21:22
Permalien
bin oui je sais je vais la
bin oui je sais je vais la terminer demain incha Allah
Nogaye Diongue (non vérifié)
mar, 12/21/2021 - 08:19
Permalien
Apprendre
Nogaye Diongue (non vérifié)
mar, 12/21/2021 - 08:19
Permalien
Apprendre
Anonyme (non vérifié)
sam, 02/01/2025 - 22:12
Permalien
Bien
Anonyme (non vérifié)
sam, 02/01/2025 - 22:12
Permalien
Trop bien
Ali (non vérifié)
lun, 05/12/2025 - 22:54
Permalien
J'aimerais savoir la physique
Ajouter un commentaire