Corrigé Bac Maths S1, S3 1er groupe 2007
Classe:
Terminale
Exercice 1
Soient $\alpha\ $ et $\ \beta$ deux nombres complexes quelconques.
On pose : $\mathrm{j}=\mathrm{e}^{\tfrac{2\mathrm{i}\pi}{3}}$ et pour tout complexe $z$ :
$$f(z)=z^{3}+\alpha z^{2}+\beta z$$
1) Montrons que $f(1)+f(\mathrm{j})+f(\mathrm{j}^{2})=3$ sachant que $1+\mathrm{j}+\mathrm{j}^{2}=0\ $ et $\ \mathrm{j}^{3}=1$
Soit :
$\begin{array}{rcl} f(1)+f(\mathrm{j})+f(\mathrm{j}^{2})&=&1+\alpha+\beta+\mathrm{j}^{3}+\alpha\mathrm{j}^{2}+\beta\mathrm{j}+(\mathrm{j}^{2})^{3}+\alpha(\mathrm{j}^{2})^{2}+\beta\mathrm{j}^{2}\\ \\&=&1+\mathrm{j}^{3}+\alpha(1+\mathrm{j}^{2}+\underbrace{\mathrm{j}^{4}}_{=\mathrm{j}})+\beta\underbrace{(1+\mathrm{j}+\mathrm{j}^{2})}_{=0}+\underbrace{\mathrm{j}^{6}}_{=(\mathrm{j}^{3})^{2}} \\ \\&=&1+\mathrm{j}^{3}+\alpha\underbrace{(1+\mathrm{j}^{2}+\mathrm{j})}_{=0}+(\mathrm{j}^{3})^{2}\\ \\&=&1+\mathrm{j}^{3}+(\mathrm{j}^{3})^{2}\quad\text{or, }\ \mathrm{j}^{3}=1\\ \\&=&1+1+1\\ \\&=&3\end{array}$
Ainsi, $\boxed{f(1)+f(\mathrm{j})+f(\mathrm{j}^{2})=3}$
2) a) En déduisons que $|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})| \geq 3$
En utilisant l'inégalité triangulaire, on obtient :
$$|f(1)+f(\mathrm{j})+f(\mathrm{j}^{2})|\leq|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|$$
Or, $|f(1)+f(\mathrm{j})+f(\mathrm{j}^{2})|=3$
Donc, $\boxed{|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|\geq 3}$
b) En utilisant a), montrons que l'un au moins des nombres réels $|f(1)|\;;\ |f(\mathrm{j})|\ $ et $\ |f(\mathrm{j}^{2})|$ est supérieur ou égal à 1.
Supposons que les nombres réels $|f(1)|\;;\ |f(\mathrm{j})|\ $ et $\ |f(\mathrm{j}^{2})|$ sont tous inférieurs à 1.
Alors, $|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|\leq 1+1+1=3$
Ce qui est contradictoire au résultat obtenu en a).
Par conséquent, l'hypothèse de départ, à savoir ; les nombres réels $|f(1)|\;;\ |f(\mathrm{j})|\ $ et $\ |f(\mathrm{j}^{2})|$ sont tous inférieurs à 1, est fausse.
D'où : l'un au moins des nombres réels $|f(1)|\;;\ |f(\mathrm{j})|\ $ et $\ |f(\mathrm{j}^{2})|$ est supérieur ou égal à 1.
3) Le plan complexe est muni d'un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v}).$
$ABC$ est un triangle équilatéral direct de centre de gravité $O$ et tel que l'affixe de $A$ soit un réel $r$ strictement positif fixé.
$I\ $ et $\ J$ sont deux points quelconques du plan d'affixes respectives $a\ $ et $\ b.$
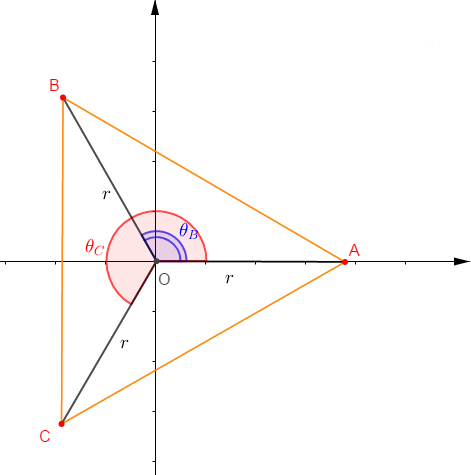
Dans cette question on prend $\alpha=-\dfrac{a+b}{r}\ $ et $\ \beta=\dfrac{ab}{r^{2}}$
a) Montrons que les affixes respectives de $B\ $ et $\ C$ sont $r\mathrm{j}\ $ et $\ r\mathrm{j}^{2}.$
Soit : $z_{B}=|z_{B}|\mathrm{e}^{\mathrm{i}\theta_{B}}\ $ avec, $\theta_{B}=arg\;z_{B}\ $ et $\ |z_{B}|=OB$
Le point $A$ étant sur l'axe réel $(Z_{A}=r\in\mathbb{R}_{+}^{*})\ $ et $\ ABC$ équilatéral direct de centre de gravité $O$ alors,
$$OA=OB=r\quad\text{et}\quad\theta_{B}=\left(\overrightarrow{OA}\;,\ \overrightarrow{OB}\right)=\dfrac{2\pi}{3}$$
Ainsi,
$\begin{array}{rcl} z_{B}&=&|z_{B}|\mathrm{e}^{\mathrm{i}\theta_{B}}\\ \\&=&OB.\mathrm{e}^{\mathrm{i}\tfrac{2\pi}{3}}\\ \\&=&r.\mathrm{e}^{\tfrac{2\mathrm{i}\pi}{3}}\\ \\&=&r.\mathrm{j}\end{array}$
D'où, $\boxed{z_{B}=r.\mathrm{j}}$
De même, on a : $z_{C}=|z_{C}|\mathrm{e}^{\mathrm{i}\theta_{C}}\ $ avec, $\theta_{C}=arg\;z_{C}\ $ et $\ |z_{C}|=OC$
Donc,
$$OA=OC=r\quad\text{et}\quad\theta_{C}=\left(\overrightarrow{OA}\;,\ \overrightarrow{OC}\right)=\dfrac{4\pi}{3}$$
Par suite,
$\begin{array}{rcl} z_{C}&=&|z_{C}|\mathrm{e}^{\mathrm{i}\theta_{C}}\\ \\&=&OC.\mathrm{e}^{\mathrm{i}\tfrac{4\pi}{3}}\\ \\&=&r.\mathrm{e}^{\tfrac{4\mathrm{i}\pi}{3}}\quad\text{or, }\ \mathrm{e}^{\tfrac{4\mathrm{i}\pi}{3}}=\left(\mathrm{e}^{\tfrac{2\mathrm{i}\pi}{3}}\right)^{2}\\ \\&=&r.\left(\mathrm{e}^{\tfrac{2\mathrm{i}\pi}{3}}\right)^{2}\\ \\&=&r.\mathrm{j}^{2}\end{array}$
D'où, $\boxed{z_{C}=r.\mathrm{j}^{2}}$
b) Montrons que $BO\cdot BI\cdot BJ=r^{3}|f(\mathrm{j})|.$
On a :
$\begin{array}{rcl} BO\cdot BI\cdot BJ&=&|z_{B}|.|z_{\overrightarrow{BI}}|.|z_{\overrightarrow{BJ}}|\\ \\&=&|z_{B}\times z_{\overrightarrow{BI}}\times z_{\overrightarrow{BJ}}|\\ \\&=&|r.\mathrm{j}(a-r.\mathrm{j})(b-r.\mathrm{j})|\\ \\&=&|r.\mathrm{j}(ab-r.\mathrm{j}.a-r.\mathrm{j}.b+(r.\mathrm{j})^{2})|\\ \\&=&|r.\mathrm{j}(ab-r.\mathrm{j}(a+b)+(r.\mathrm{j})^{2})|\quad\text{or, }\ (a+b)=-r.\alpha\ \text{ et }\ ab=r^{2}.\beta\\ \\&=&|r.\mathrm{j}(r^{2}.\beta+r^{2}.\mathrm{j}.\alpha+r^{2}.\mathrm{j}^{2})|\\ \\&=&|r^{3}(\mathrm{j}.\beta+\mathrm{j}^{2}.\alpha+\mathrm{j}^{3})|\\ \\&=&r^{3}|\mathrm{j}^{3}+\alpha\mathrm{j}^{2}+\beta\mathrm{j}|\\ \\&=&r^{3}|f(\mathrm{j})|\end{array}$
Ainsi, $\boxed{BO\cdot BI\cdot BJ=r^{3}|f(\mathrm{j})|}$
Calculons de la même manière $CO\cdot CI\cdot CJ\ $ et $\ AO\cdot AI\cdot AJ$
Soit :
$\begin{array}{rcl} CO\cdot CI\cdot CJ&=&|z_{C}|.|z_{\overrightarrow{CI}}|.|z_{\overrightarrow{CJ}}|\\ \\&=&|z_{C}\times z_{\overrightarrow{CI}}\times z_{\overrightarrow{CJ}}|\\ \\&=&|r.\mathrm{j}^{2}(a-r.\mathrm{j}^{2})(b-r.\mathrm{j}^{2})|\\ \\&=&|r.\mathrm{j}^{2}(ab-r.\mathrm{j}^{2}.a-r.\mathrm{j}^{2}.b+(r.\mathrm{j}^{2})^{2})|\\ \\&=&|r.\mathrm{j}^{2}(ab-r.\mathrm{j}^{2}(a+b)+(r.\mathrm{j}^{2})^{2})|\quad\text{avec, }\ (a+b)=-r.\alpha\ \text{ et }\ ab=r^{2}.\beta\\ \\&=&|r.\mathrm{j}^{2}(r^{2}.\beta+r^{2}.\mathrm{j}^{2}.\alpha+r^{2}.\mathrm{j}^{4})|\\ \\&=&|r^{3}(\mathrm{j}^{2}.\beta+\mathrm{j}^{4}.\alpha+\mathrm{j}^{6})|\\ \\&=&r^{3}|(\mathrm{j}^{2})^{3}+\alpha(\mathrm{j}^{2})^{2}+\beta\mathrm{j}^{2}|\\ \\&=&r^{3}|f(\mathrm{j}^{2})|\end{array}$
Donc, $\boxed{CO\cdot CI\cdot CJ=r^{3}|f(\mathrm{j}^{2})|}$
Aussi, on a :
$\begin{array}{rcl} AO\cdot AI\cdot AJ&=&|z_{A}|.|z_{\overrightarrow{AI}}|.|z_{\overrightarrow{AJ}}|\\ \\&=&|z_{A}\times z_{\overrightarrow{AI}}\times z_{\overrightarrow{AJ}}|\\ \\&=&|r(a-r)(b-r)|\\ \\&=&|r(ab-r.a-r.b+r^{2})|\\ \\&=&|r(ab-r(a+b)+r^{2})|\quad\text{avec, }\ (a+b)=-r.\alpha\ \text{ et }\ ab=r^{2}.\beta\\ \\&=&|r(r^{2}.\beta+r^{2}.\alpha+r^{2})|\\ \\&=&|r^{3}(\beta+\alpha+1)|\\ \\&=&r^{3}|(1+\alpha+\beta|\\ \\&=&r^{3}|f(1)|\end{array}$
Donc, $\boxed{AO\cdot AI\cdot AJ=r^{3}|f(1)|}$
c) Montrons que le triangle $ABC$ a au moins un sommet $S$ vérifiant :
$$SO\cdot SI\cdot SJ\geq r^{3}$$
D'après la question 3)b), les sommets $A\;,\ B\ $ et $\ C$ du triangle $ABC$ vérifient :
$$AO\cdot AI\cdot AJ=r^{3}|f(1)|\;,\ BO\cdot BI\cdot BJ=r^{3}|f(\mathrm{j})|\ \text{ et }\ CO\cdot CI\cdot CJ=r^{3}|f(\mathrm{j}^{2})|$$
Donc, si tout sommet $S$ vérifie : $SO\cdot SI\cdot SJ< r^{3}$, on aura :
$$AO\cdot AI\cdot AJ+BO\cdot BI\cdot BJ+CO\cdot CI\cdot CJ<3r^{3}$$
Or,
$\begin{array}{rcl} AO\cdot AI\cdot AJ+BO\cdot BI\cdot BJ+CO\cdot CI\cdot CJ&=&r^{3}|f(1)|+r^{3}|f(\mathrm{j})|+r^{3}|f(\mathrm{j}^{2})|\\ \\&=&r^{3}(|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|)\end{array}$
Ainsi, $r^{3}(|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|)<3r^{3}\ \Rightarrow\ |f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|<3$
Ce qui est en contradiction avec le résultat obtenu au 2.a), à savoir ;
$$|f(1)|+|f(\mathrm{j})|+|f(\mathrm{j}^{2})|\geq 3$$
Par suite, l'hypothèse de départ est fausse et par conséquent, le triangle $ABC$ a au moins un sommet $S$ vérifiant :
$$SO\cdot SI\cdot SJ\geq r^{3}$$
Autre méthode
Tout sommet $S$ vérifie :
$$SO\cdot SI\cdot SJ=r^{3}\lambda$$
où, $\lambda$ représente $|f(1)|\ $ ou $\ |f(\mathrm{j})|\ $ ou $\ |f(\mathrm{j}^{2})|$
Or, d'après 2.b), on sait que au moins l'un des nombres réels $|f(1)|\;;\ |f(\mathrm{j})|\ $ et $\ |f(\mathrm{j}^{2})|$ est supérieur ou égal à 1. Donc, il existe au moins un $\lambda$ vérifiant : $\lambda\geq 1$
Par suite, $\lambda\geq 1\ \Rightarrow\ \exists\;S\;;\ SO\cdot SI\cdot SJ\geq r^{3}$
Par conséquent, le triangle $ABC$ a au moins un sommet $S$ vérifiant :
$$SO\cdot SI\cdot SJ\geq r^{3}$$
Exercice 2
Le plan $(P)$ étant orienté ; on considère un triangle rectangle isocèle $ABC$ tel que $\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)$ ait pour mesure $\dfrac{\pi}{2}$
On note $O$ l'intersection des bissectrices intérieures de $ABC$.
Soit $s_{1}$ la similitude plane directe de centre $A$ qui transforme $B$ en $O$ et $s_{2}$ la similitude plane directe de centre $C$ qui transforme $O$ en $B.$
A tout point $M$ du plan distinct de $A$ et de $B$ ; on associe le point $N=s_{1}(M)$ et le point $P=s_{2}^{-1}(M)$
1) a) Déterminons une mesure de l'angle $\left(\overrightarrow{AM}\;;\ \overrightarrow{AN}\right)$
On a : $s_{1}=s_{(A\;,\ k_{1}\;,\ \theta_{1})}$
Comme $s_{1}$ transforme $B$ en $O$ alors, on a :
$$\left\lbrace\begin{array}{rcl} AO&=&k_{1} AB \\ \\ \left(\overrightarrow{AB}\;,\ \overrightarrow{AO}\right)&=&\theta_{1}\;[2\pi]\end{array}\right.$$
Or, le triangle $ABC$ est isocèle en $B$ et que $(\overrightarrow{BA}\;,\ \overrightarrow{BC})=\dfrac{\pi}{2}$ donc,
$$(\overrightarrow{AB}\;,\ \overrightarrow{AC})=(\overrightarrow{CA}\;,\ \overrightarrow{CB})=\dfrac{\pi}{4}$$
De plus, $(OA)$ est bissectrice de l'angle $\widehat{BAC}$ donc,
$$\left(\overrightarrow{AB}\;,\ \overrightarrow{AO}\right)=\dfrac{1}{2}\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)=\dfrac{\pi}{8}$$
Ainsi, $\boxed{\theta_{1}=\dfrac{\pi}{8}\ \text{ et }\ k_{1}=\dfrac{AO}{AB}}$
Par ailleurs, $s_{1}(M)=N$ alors, $\left(\overrightarrow{AM}\;,\ \overrightarrow{AN}\right)=\theta_{1}\;[2\pi]$
D'où, une mesure de l'angle $\left(\overrightarrow{AM}\;,\ \overrightarrow{AN}\right)$ est : $\dfrac{\pi}{8}$
b) On désigne par $s'$ la similitude plane directe de centre $A$ qui transforme $B$ en $M.$
Montrons que $s'\circ s_{1}=s_{1}\circ s'$
Soit $s_{1}=s_{(A\;,\ k_{1}\;,\ \theta_{1})}\ $ et $\ s'=s_{(A\;,\ k'\;,\ \theta')}$ avec, $k'=\dfrac{AM}{AB}\ $ et $\ \theta'=\left(\overrightarrow{AB}\;,\ \overrightarrow{AM}\right)$
alors, on a :
$s'\circ s_{1}=s_{(A\;,\ k'k_{1}\;,\ \theta'+\theta_{1})}\ $ et $\ s_{1}\circ s'=s_{(A\;,\ k_{1}k'\;,\ \theta_{1}+\theta')}$
$s'\circ s_{1}\ $ et $\ s_{1}\circ s'$ ayant les mêmes éléments caractéristiques donc,
$$s'\circ s_{1}=s_{1}\circ s'$$
En déduisons l'image de $O$ par $s'.$
On a : $s'\circ s_{1}(B)=s'(O)\ $ et $\ s_{1}\circ s'(B)=s_{1}(M)=N$
Or, $s'\circ s_{1}=s_{1}\circ s'$ donc,
$$s'(O)=N$$
Déterminons une mesure de l'angle $\left(\overrightarrow{MA}\;,\ \overrightarrow{MN}\right)$
Les similitudes conservant les angles orientés alors :
$$\left(\overrightarrow{MA}\;,\ \overrightarrow{MN}\right)=\left(\overrightarrow{BA}\;,\ \overrightarrow{BO}\right)$$
Or, $\left(\overrightarrow{BA}\;,\ \overrightarrow{BO}\right)=\dfrac{1}{2}\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)=\dfrac{\pi}{4}$
Donc, une mesure de l'angle $\left(\overrightarrow{MA}\;,\ \overrightarrow{MN}\right)$ est : $\dfrac{\pi}{4}$
c) Proposons une construction géométrique de $N$, lorsque le point $M$ est donné.
Pour construire le point $N$ connaissant $M$, on trace deux demi-droite $[Mx)\ $ et $\ [Ay)$ telles que :
$$\left(\overrightarrow{MA}\;,\ [Mx)\right)=\dfrac{\pi}{4}\ \text{ et }\ \left(\overrightarrow{AM}\;,\ [Ay)\right)=\dfrac{\pi}{8}$$
Le point de rencontre de ces deux demi-droite donne le point $N.$
2) a) Donnons la nature de $r=s_{1}\circ s_{2}$
On a : $s_{1}=s_{(A\;,\ k_{1}\;,\ \theta_{1})}\ $ et $\ s_{2}=s_{(C\;,\ k_{2}\;,\ \theta_{2})}$
Comme $s_{2}$ transforme $O$ en $B$ alors, on a :
$$\left\lbrace\begin{array}{rcl} CB&=&k_{2} CO \\ \\ \left(\overrightarrow{CO}\;,\ \overrightarrow{CB}\right)&=&\theta_{2}\;[2\pi]\end{array}\right.$$
Or, $\left(\overrightarrow{CO}\;,\ \overrightarrow{CB}\right)=\dfrac{1}{2}\left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)=\dfrac{\pi}{8}$
Donc, $\boxed{\theta_{2}=\dfrac{\pi}{8}\ \text{ et }\ k_{2}=\dfrac{CB}{CO}}$
Ainsi, $r=s_{1}\circ s_{2}$ est une similitude plane directe de rapport $k=k_{1}.k_{2}\ $ et d'angle $\ \theta=\theta_{1}+\theta_{2}$
On a :
$\begin{array}{rcl} k&=&k_{1}.k_{2}\\ \\&=&\dfrac{AO}{AB}\times\dfrac{CB}{CO}\quad\text{or, }\ AB=CB\ \text{ et }\ CO=AO\\ \\&=&\dfrac{AO}{AB}\times\dfrac{AB}{AO}\\ \\&=&1\end{array}$
Donc, $\boxed{k=1\ \text{ et }\ \theta=\dfrac{\pi}{4}}$
Par ailleurs, $s_{1}\circ s_{2}(O)=s_{1}(B)=O$
Ce qui montre que le point $O$ est invariant par $r$ donc, il constitue le centre de cette similitude.
D'où, $r=s_{1}\circ s_{2}$ est la rotation de centre $O$ et d'angle $\theta=\dfrac{\pi}{4}$
b) Déterminons $r(P)$
Soit :
$\begin{array}{rcl} r(P)&=&s_{1}\circ s_{2}(P)\\ \\&=&s_{1}\circ s_{2}\circ s_{2}^{-1}(M)\\ \\&=&s_{1}(M)\\ \\&=&N\end{array}$
Donc, $\boxed{r(P)=N}$
Ainsi, à partir de $N$, on fait une rotation d'angle $\dfrac{\pi}{4}$ pour une construction géométrique de $P$
Plus précisément, on trace un demi-cercle $(C)$ de rayon $ON$, à partir de $N$ puis on trace la demi-droite $[Oz)$ telle que :
$$\left([Oz)\;,\ \overrightarrow{ON}\right)=\dfrac{\pi}{4}$$
Le point $P$ est le point de rencontre de la demi-droite $[Oz)$ et du demi-cercle $(C).$
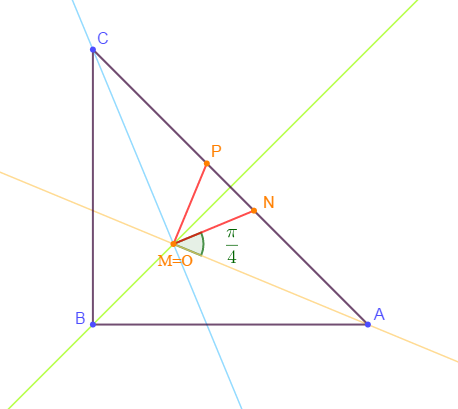
c) Lorsque $M=O$, montrons que le point $N$ appartient à la demi-droite $[AC)$ et le point $P$ à la demi-droite $[CA)$
D'après question 1.a), on a $\left(\overrightarrow{AM}\;,\ \overrightarrow{AN}\right)=\dfrac{\pi}{8}$
Ainsi, pour $M=O$ on aura : $\left(\overrightarrow{AO}\;,\ \overrightarrow{AN}\right)=\dfrac{\pi}{8}$
Or, $\left(\overrightarrow{AO}\;,\ [AC)\right)=\dfrac{\pi}{8}$
Donc, $\left(\overrightarrow{AO}\;,\ \overrightarrow{AN}\right)=\left(\overrightarrow{AO}\;,\ [AC)\right)$
D'où, $N\in[AC)$
Par ailleurs, $P=s_{2}^{-1}(M)\ \Rightarrow\ s_{2}(P)=M$
Ainsi, pour $M=O$, on obtient : $s_{2}(P)=O$
Ce qui donne $\left(\overrightarrow{CP}\;,\ \overrightarrow{CO}\right)=\dfrac{\pi}{8}$
Or, $\left([CA)\;,\ \overrightarrow{CO}\right)=\dfrac{\pi}{8}$
Donc, $\left(\overrightarrow{CP}\;,\ \overrightarrow{CO}\right)=\left([CA)\;,\ \overrightarrow{CO}\right)$
Par suite, $P\in[CA)$
3) Faisons une figure comportant les points $A\;,\ B\;,\ C\;,\ O\;,\ P\ $ et $\ N$ avec $M=O.$
Exercice 3
On considère dans le plan muni d'un repère orthonormal $(O\;,\ \vec{u}\;,\ \vec{v})$, les trois points $A\;,\ B\ $ et $\ C$ de coordonnées respectives $(1\;,\ 0)\;,\ (0\;,\ 1)\ $ et $\ (1\;,\ 1)$, puis à tout réel $t\in[0\;,\ 1]$ on associe le point $M(t)$ barycentre du système $\{(B\;,\ (1-t)^{2})\;,\ (A\;,\ 2t(1-t))\;,\ (C\;,\ t^{2})\}$
On note $x(t)\ $ et $\ y(t)$ les coordonnées de $M(t)\ $ et $\ (\Gamma)$ l'ensemble des points $M(t)$ lorsque $t$ décrit $[0\;,\ 1].$
1) a) Exprimons en fonction de $t$ les coordonnées $x(t)\ $ et $\ y(t)$ de $M(t)$
$M(t)\begin{pmatrix} x(t)\\y(t)\end{pmatrix}$ barycentre du système $\{(B\;,\ (1-t)^{2})\;,\ (A\;,\ 2t(1-t))\;,\ (C\;,\ t^{2})\}$ alors, ses coordonnées $x(t)\ $ et $\ y(t)$ s'écrivent :
$$\left\lbrace\begin{array}{rcrcl} x(t)&=&\dfrac{2t(1-t)\times 1+(1-t)^{2}\times 0+t^{2}\times 1}{2t(1-t)+(1-t)^{2}+t^{2}}&=&-t^{2}+2t\\ \\y(t)&=&\dfrac{2t(1-t)\times 0+(1-t)^{2}\times 1+t^{2}\times 1}{2t(1-t)+(1-t)^{2}+t^{2}}&=&2t^{2}-2t+1\end{array}\right.$$
D'où, $\boxed{\left\lbrace\begin{array}{rcl} x(t)&=&-t^{2}+2t\\ \\ y(t)&=&2t^{2}-2t+1\end{array}\right.}$
b) Dressons le tableau de variations des fonctions $x\ $ et $\ y$
Les fonctions dérivées sont données par :
$\left\lbrace\begin{array}{rcl} x'(t)&=&-2t+2\\ \\ y'(t)&=&4t-2\end{array}\right.$
On a :
$\begin{array}{rcl} x'(t)\geq 0&\Leftrightarrow&-2t+2\geq 0\\&\Leftrightarrow&-2t\geq -2\\&\Leftrightarrow&t\leq 1\end{array}$
Donc, pour $t\in[0\;;\ 1]\;,\ x'(t)\geq 0$
Par suite, $x(t)$ croissante sur $[0\;;\ 1]$
$\begin{array}{rcl} y'(t)\geq 0&\Leftrightarrow&4t-2\geq 0\\&\Leftrightarrow&4t\geq 2\\&\Leftrightarrow&t\geq\dfrac{1}{2}\end{array}$
Donc, si $t\in\left[\dfrac{1}{2}\;;\ 1\right]$ alors, $y'(t)\geq 0$
Par suite, $y(t)$ croissante sur $\left[\dfrac{1}{2}\;;\ 1\right]$ et décroissante sur $\left[0\;;\ \dfrac{1}{2}\right]$
$$\begin{array}{|c|lcccr|} \hline t&0&&1/2&&1\\ \hline x'(t)&&+&&+&\\ \hline&&&&&1\\&&&&\nearrow&\\ x(t)&&&3/4&&\\&&\nearrow&&&\\&0&&&&\\ \hline&1&&&&1\\&&&&&\\ y(t)&&\searrow&&\nearrow&\\&&&&&\\&&&1/2&&\\ \hline y'(t)&&-&0&+&\\ \hline\end{array}$$
Traçons la courbe $(\Gamma)$ ainsi que ses tangentes aux points $B\;,\ C\ $ et $\ M\left(\dfrac{1}{2}\right)$
Déterminons alors les équations paramétriques de ces tangentes.
Soit $T_{B}$ la tangente à la courbe au point $B$
Comme $B$ est le point de $(\Gamma)$ repéré à la date $t_{0}=0$ alors, $\vec{u}_{0}\begin{pmatrix} x'(0)\\y'(0)\end{pmatrix}$ est un vecteur directeur de $T_{B}.$ Soit alors : $\vec{u}_{0}\begin{pmatrix} 2\\-2\end{pmatrix}$
Si $N\begin{pmatrix} x(t)\\y(t)\end{pmatrix}\in T_{B}$ alors, il existe un paramètre $t$ tel que $\overrightarrow{BN}\ $ et $\ \vec{u}_{0}$ soient colinéaires.
Ainsi,
$\begin{array}{rcl} \overrightarrow{BN}\ \text{ et }\ \vec{u}_{0}\ \text{ colinéaires}&\Leftrightarrow&\overrightarrow{BN}=t\vec{u}_{0}\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x(t)-0&=&2t\\ \\y(t)-1&=&-2t\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x(t)&=&2t\\ \\y(t)&=&-2t+1\end{array}\right.\end{array}$
Une équation paramétrique de $T_{B}$ est donc donnée par :
$$T_{B}\ :\ \left\lbrace\begin{array}{rcl} x(t)&=&2t\\ \\y(t)&=&-2t+1\end{array}\right.$$
Son équation cartésienne est alors : $y=-x+1$
De la même manière, considérons $T_{C}$ la tangente à la courbe au point $C.$
$C$ étant le point de $(\Gamma)$ repéré à la date $t_{1}=1$ alors, $\vec{u}_{1}\begin{pmatrix} x'(1)\\y'(1)\end{pmatrix}$ est un vecteur directeur de $T_{C}.$
On obtient alors : $\vec{u}_{1}\begin{pmatrix} 0\\2\end{pmatrix}$
Si $P\begin{pmatrix} x(t)\\y(t)\end{pmatrix}\in T_{C}$ alors, il existe un paramètre $t$ tel que $\overrightarrow{CP}\ $ et $\ \vec{u}_{1}$ soient colinéaires.
Ainsi,
$\begin{array}{rcl} \overrightarrow{CP}\ \text{ et }\ \vec{u}_{1}\ \text{ colinéaires}&\Leftrightarrow&\overrightarrow{CP}=t\vec{u}_{1}\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x(t)-1&=&0\\ \\y(t)-1&=&2t\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x(t)&=&1\\ \\y(t)&=&2t+1\end{array}\right.\end{array}$
Une équation paramétrique de $T_{C}$ est alors donnée par :
$$T_{C}\ :\ \left\lbrace\begin{array}{rcl} x(t)&=&1\\ \\y(t)&=&2t+1\end{array}\right.$$
Et son équation cartésienne sera donnée par : $x=1$
Au point $M\left(\dfrac{1}{2}\right)$ on obtient une tangente $T_{M}$ de vecteur directeur $\vec{u}_{1/2}\begin{pmatrix} x'(1/2)\\y'(1/2)\end{pmatrix}.$
Donc, si $Q\begin{pmatrix} x(t)\\y(t)\end{pmatrix}\in T_{M}$ alors, il existe un paramètre $t$ tel que $\overrightarrow{MQ}\begin{pmatrix} x(t)-\dfrac{3}{4}\\ \\y(t)-\dfrac{1}{2}\end{pmatrix}\ $ et $\ \vec{u}_{1/2}\begin{pmatrix} 1\\0\end{pmatrix}$ soient colinéaires.
Ainsi,
$\begin{array}{rcl} \overrightarrow{MQ}\ \text{ et }\ \vec{u}_{1/2}\ \text{ colinéaires}&\Leftrightarrow&\overrightarrow{MQ}=t\vec{u}_{1/2}\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x(t)-\dfrac{3}{4}&=&t\\ \\y(t)-\dfrac{1}{2}&=&0\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x(t)&=&t+\dfrac{3}{4}\\ \\y(t)&=&\dfrac{1}{2}\end{array}\right.\end{array}$
Ce qui montre que $T_{M}$ a pour équation paramétrique :
$$T_{M}\ :\ \left\lbrace\begin{array}{rcl} x(t)&=&t+\dfrac{3}{4}\\ \\y(t)&=&\dfrac{1}{2}\end{array}\right.$$
Son équation cartésienne est alors donnée par : $y=\dfrac{1}{2}$
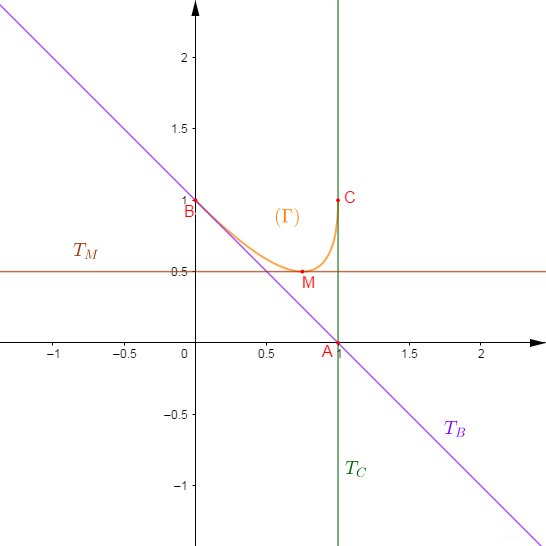
2) Montrons que les tangentes à $(\Gamma)$ en $B\ $ et $\ C$ se coupent en $A.$
Considérons les équations paramétriques de $T_{B}\ $ et $\ T_{C}$ suivantes :
$$T_{B}\ :\ \left\lbrace\begin{array}{rcl} x(t)&=&2t\\ \\y(t)&=&-2t+1\end{array}\right.\qquad T_{C}\ :\ \left\lbrace\begin{array}{rcl} x(t)&=&1\\ \\y(t)&=&2t+1\end{array}\right.$$
On constate dans l'équation de $T_{C}$ que $x(t)=1$ donc, en remplaçant dans l'équation de $T_{B}$, on obtient :
$$\left\lbrace\begin{array}{rcl} 1&=&2t\\ \\y(t)&=&-2t+1\end{array}\right.\ \Leftrightarrow\ \left\lbrace\begin{array}{rcl} t&=&\dfrac{1}{2}\\ \\y(t)&=&-2\times\dfrac{1}{2}+1=0\end{array}\right.$$
D'où, $A\begin{pmatrix} 1\\0\end{pmatrix}=T_{B}\cap T_{C}$
Autre méthode
On peut aussi passer par les équations cartésiennes de droites de $T_{B}\ $ et $\ T_{C}$ données respectivement par :
$$y=-x+1\quad\text{et}\quad x=1$$
On obtient alors le système d'équations suivant :
$$\left\lbrace\begin{array}{rcl} x&=&1\\ y&=&-x+1\end{array}\right.$$
Ainsi, en remplaçant la valeur de $x$ dans la deuxième équation, on obtient : $y=-1+1=0$
Par suite, le couple de solution $(1\;;\ 0)$ donne les coordonnées du point d'intersection des droites $T_{B}\ $ et $\ T_{C}.$
D'où, $A\begin{pmatrix} 1\\0\end{pmatrix}=T_{B}\cap T_{C}$
3) Trouvons une relation entre $x(t)\ $ et $\ y(t)$ indépendante de $t.$ Soit $y=f(x)$
Posons : $x=-t^{2}+2t\ \Rightarrow\ t^{2}-2t+x=0$
Soit : $\Delta=4-4x$ alors, les solutions de l'équation sont données par :
$$t_{1}=\dfrac{2-\sqrt{4-4x}}{2}=1-\sqrt{1-x}\quad\text{et}\quad t_{2}=\dfrac{2+\sqrt{4-4x}}{2}=1+\sqrt{1-x}$$
Comme $t\in[0\;;\ 1]$ alors, on choisira $t=t_{1}=1-\sqrt{1-x}$
Remplaçons cette expression de $t$ dans l'équation : $y=2t^{2}-2t+1.$ On obtient alors :
$\begin{array}{rcl} y&=&2t^{2}-2t+1\\ \\&=&2(1-\sqrt{1-x})^{2}-2(1-\sqrt{1-x})+1\\ \\&=&2(1+1-x-2\sqrt{1-x})-2(1-\sqrt{1-x})+1\\ \\&=&4-2x-4\sqrt{1-x}-2+2\sqrt{1-x}+1\\ \\&=&3-2x-2\sqrt{1-x}\end{array}$
D'où, $\boxed{y=3-2x-2\sqrt{1-x}}$
Calculons $\lim\limits_{x\rightarrow 1^{-}}\dfrac{f(x)-f(1)}{x-1}$
On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow 1^{-}}\dfrac{f(x)-f(1)}{x-1}&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{3-2x-2\sqrt{1-x}-1}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{2-2x-2\sqrt{1-x}}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}\dfrac{2(1-x)}{x-1}-\dfrac{2\sqrt{1-x}}{x-1}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}-2-\dfrac{2(1-x)}{x-1\sqrt{1-x}}\\ \\&=&\lim\limits_{x\rightarrow 1^{-}}-2+\dfrac{2}{\sqrt{1-x}}\\ \\&=&-2+\dfrac{1}{0^{+}}\\ \\&=&+\infty\end{array}$
D'où, $\boxed{\lim\limits_{x\rightarrow 1^{-}}\dfrac{f(x)-f(1)}{x-1}=+\infty}$
Par conséquent, la fonction $f$ n'est pas dérivable à gauche au point 1.
Problème
Partie A
Soit $f$ une fonction définie sur $[1\;,\ +\infty[$ ayant une dérivée continue et croissante.
Pour tout $p\in\mathbb{N}^{\ast}$, on pose :
$$u_{p}=\sum_{n=1}^{p}f'(n)$$
1) Démontrons la relation suivante :
$$(01)\qquad \forall\;n\in\mathbb{N}^{\ast}\ :\ f'(n)\leq f(n+1)-f(n)\leq f'(n+1)$$
a) En appliquant le théorème des accroissements finis à $f$ dans un intervalle bien choisi.
Soit $I$ un intervalle de $\mathbb{R}$ défini par : $I=[n\;;\ n+1]\;,\ n\in\mathbb{N}^{\ast}$
$f$ est continue et dérivable sur $I$ alors, d'après le théorème des accroissements finis, il existe $c\in I$ tel que :
$$f(n+1)-f(n)=((n+1)-n)f'(c)\ \Leftrightarrow\ f(n+1)-f(n)=f'(c)$$
Or, $f'$ est croissante sur $I$ donc,
$\begin{array}{rcccccl}\forall\;n\in\mathbb{N}^{\ast}\ :\ n\leq c\leq n+1&\Rightarrow&f'(n)&\leq&f'(c)&\leq&f'(n+1)\\&\Rightarrow&f'(n)&\leq&f(n+1)-f(n)&\leq&f'(n+1)\end{array}$
D'où, la relation suivante :
$$\boxed{\forall\;n\in\mathbb{N}^{\ast}\ :\ f'(n)\leq f(n+1)-f(n)\leq f'(n+1)}$$
b) En utilisant la valeur moyenne de $f'$ sur $[n\;;\ n+1]$
Considérons $I$ un intervalle de $\mathbb{R}$ défini par : $I=[n\;;\ n+1]\;,\ n\in\mathbb{N}^{\ast}$
$f'$ est continue sur $I$ alors, d'après le théorème de la moyenne, il existe au moins un réel $c\in I$ tel que :
$$f'(c)=\dfrac{1}{(n+1)-n}\int_{n}^{n+1}f'(x)\mathrm{d}x=[f(x)]_{n}^{n+1}$$
Or, $f'$ est croissante sur $I$ donc,
$\begin{array}{rcccccl}\forall\;n\in\mathbb{N}^{\ast}\ :\ n\leq c\leq n+1&\Rightarrow&f'(n)&\leq&f'(c)&\leq&f'(n+1)\\ \\&\Rightarrow&f'(n)&\leq&[f(x)]_{n}^{n+1}&\leq&f'(n+1)\\ \\&\Rightarrow&f'(n)&\leq&f(n+1)-f(n)&\leq&f'(n+1)\end{array}$
Ce qui montre que :
$$\boxed{\forall\;n\in\mathbb{N}^{\ast}\ :\ f'(n)\leq f(n+1)-f(n)\leq f'(n+1)}$$
2) En utilisant la relation (01), de la question 1) démontrons que
$$(02)\qquad \forall\;p\in\mathbb{N}^{\ast}\;,\ u_{p}-f'(p)\leq f(p)-f(1)\leq u_{p}-f'(1)$$
En appliquant la relation (01), on obtient :
$\begin{array}{rcccl} f'(1)&\leq&f(2)-f(1)&\leq&f'(2)\\ \\f'(2)&\leq&f(3)-f(2)&\leq&f'(3)\\ \\f'(3)&\leq&f(4)-f(3)&\leq&f'(4)\\ \\ &\vdots&\vdots&\vdots&\\ \\f'(p-1)&\leq&f(p)-f(p-1)&\leq&f'(p)\end{array}$
En sommant ces inégalités membre à membre, on obtient :
$$f'(1)+f'(2)+\ldots+f'(p-1)\leq f(p)-f(1)\leq f'(2)+f'(3)+\ldots+f'(p)$$
Il faut juste remarquer que :
$\begin{array}{rcl} f'(1)+f'(2)+\ldots+f'(p-1)&=&\underbrace{f'(1)+f'(2)+\ldots+f'(p-1)+f'(p)}_{=\sum_{n=1}^{p}f'(n)}-f'(p)\\ \\&=&\sum_{n=1}^{p}f'(n)-f'(p)\\ \\&=&u_{p}-f'(p)\end{array}$
Aussi,
$\begin{array}{rcl} f'(2)+f'(3)+\ldots+f'(p)&=&-f'(1)+\underbrace{f'(1)+f'(2)+\ldots+f'(p-1)+f'(p)}_{\sum_{n=1}^{p}f'(n)}\\ \\&=&\sum_{n=1}^{p}f'(n)-f'(1)\\ \\&=&u_{p}-f'(1)\end{array}$
Par suite,
$$\boxed{\forall\;p\in\mathbb{N}^{\ast}\;,\ u_{p}-f'(p)\leq f(p)-f(1)\leq u_{p}-f'(1)}$$
3) Dans cette question on prend $f(x)=\dfrac{1}{x^{2}}$
a) Vérifions que la suite $(u_{p})$ est monotone.
Soit :
$\begin{array}{rcl} u_{p+1}-u_{p}&=&\sum_{n=1}^{p+1}f'(n)-\sum_{n=1}^{p}f'(n)\\ \\&=&(f'(1)+f'(2)+\ldots+f'(p)+f'(p+1))-(f'(1)+f'(2)+\ldots+f'(p))\\ \\&=&f'(p+1)\end{array}$
Or, $f(x)=\dfrac{1}{x^{2}}$ donc, $f'(x)=-\dfrac{2}{x^{3}}$
Ainsi, $f'(p+1)=-\dfrac{2}{(p+1)^{3}}<0$
Par suite, $u_{p+1}-u_{p}<0$ d'où, la suite $(u_{p})$ est décroissante. Elle est donc monotone.
b) En utilisant la relation (02), de la question 2) montrons que la suite $(u_{p})$ est bornée.
On constate d'abord que $f''(x)=\dfrac{6}{x^{4}}>0$ donc, $f'$ est croissante.
On peut alors appliquer la relation (02). On obtient d'une part :
$\begin{array}{rcl} u_{p}-f'(p)\leq f(p)-f(1)&\Rightarrow&u_{p}\leq f'(p)+f(p)-f(1)\\ \\&\Rightarrow&u_{p}\leq -\dfrac{2}{p^{3}}+\dfrac{1}{p^{2}}-1\end{array}$
D'autre part :
$\begin{array}{rcl} f(p)-f(1)\leq u_{p}-f'(1)&\Rightarrow&f(p)-f(1)+f'(1)\leq u_{p}\\ \\&\Rightarrow&\dfrac{1}{p^{2}}-1-2\leq u_{p}\\ \\&\Rightarrow&\dfrac{1}{p^{2}}-3\leq u_{p}\end{array}$
On obtient l'encadrement suivant :
$$\dfrac{1}{p^{2}}-3\leq u_{p}\leq -\dfrac{2}{p^{3}}+\dfrac{1}{p^{2}}-1$$
Posons $w_{p}=\dfrac{1}{p^{2}}-3\ $ et $\ w_(p)'=-\dfrac{2}{p^{3}}+\dfrac{1}{p^{2}}-1$
Alors, on a :
$\begin{array}{rcl}\ell&=&\lim\limits_{p\rightarrow +\infty}w_{p}\\ \\&=&\lim\limits_{p\rightarrow +\infty}\dfrac{1}{p^{2}}-3\\ \\&=&-3\end{array}$
$\begin{array}{rcl}\ell'&=&\lim\limits_{p\rightarrow +\infty}w_{p}'\\ \\&=&\lim\limits_{p\rightarrow +\infty}-\dfrac{2}{p^{3}}+\dfrac{1}{p^{2}}-1\\ \\&=&-1\end{array}$
Par conséquent :
$$\boxed{-3\leq u_{p}\leq -1}$$
Ce qui montre que la suite $(u_{p})$ est bornée.
c) En déduisons que la suite $(v_{p})$ de terme général $v_{p}=\sum_{n=1}^{p}\dfrac{1}{n^{3}}$ est convergente
On sait que $u_{p}=\sum_{n=1}^{p}f'(n)$ avec, $f'(x)=-\dfrac{2}{x^{3}}$
Donc,
$\begin{array}{rcl} u_{p}&=&\sum_{n=1}^{p}-\dfrac{2}{n^{3}}\\ \\&=&-2\sum_{n=1}^{p}\dfrac{1}{n^{3}}\\ \\&=&-2v_{p}\end{array}$
Par suite, $v_{p}=-\dfrac{1}{2}u_{p}$
Or, la suite $(u_{p})$ est monotone et bornée donc elle est convergente.
Par conséquent, la suite $(v_{p})$ de terme général $v_{p}=\sum_{n=1}^{p}\dfrac{1}{n^{3}}$ est convergente.
Montrons que sa limite $\ell''$ appartient à l'intervalle $\left[\dfrac{1}{2}\;,\ \dfrac{3}{2}\right]$
On a : $-3\leq u_{p}\leq -1\ $ or, $u_{p}=-2v_{p}$
Donc,
$\begin{array}{rcl} -3\leq -2v_{p}\leq -1&\Rightarrow&1\leq 2v_{p}\leq 3\\ \\&\Rightarrow&\dfrac{1}{2}\leq v_{p}\leq \dfrac{3}{2}\\ \\&\Rightarrow&\dfrac{1}{2}\leq \lim\limits_{p\rightarrow +\infty}v_{p}\leq \dfrac{3}{2}\\ \\&\Rightarrow&\dfrac{1}{2}\leq\ell''\leq \dfrac{3}{2}\end{array}$
D'où, $\boxed{\ell''\in\left[\dfrac{1}{2}\;,\ \dfrac{3}{2}\right]}$
4) Dans cette question on prend $f(x)=-\ln x$
a) En utilisant la relation (02), montrons que $$u_{p}\leq-\dfrac{1}{p}-\ln p$$
On constate d'abord que $f'(x)=-\dfrac{1}{x}\ $ et $\ f''(x)=\dfrac{1}{x^{2}}>0$
Donc, $f'$ est croissante.
Ainsi, en utilisant la relation (02), on obtient :
$\begin{array}{rcl} u_{p}-f'(p)\leq f(p)-f(1)&\Rightarrow&u_{p}\leq f'(p)+f(p)-f(1)\\ \\&\Rightarrow&u_{p}\leq-\dfrac{1}{p}-\ln p-0\end{array}$
D'où, $\boxed{u_{p}\leq-\dfrac{1}{p}-\ln p}$
b) Montrons que $$\lim_{p\rightarrow +\infty}\sum_{n=1}^{p}\dfrac{1}{n}=+\infty$$
Comme $u_{p}=\sum_{n=1}^{p}f'(n)$ avec $f'(n)=-\dfrac{1}{n}\ $ et $\ u_{p}\leq-\dfrac{1}{p}-\ln p$ alors, on a :
$\begin{array}{rcl} \sum_{n=1}^{p}-\dfrac{1}{n}\leq -\dfrac{1}{p}-\ln p&\Rightarrow&-\sum_{n=1}^{p}\dfrac{1}{n}\leq -\dfrac{1}{p}-\ln p\\ \\&\Rightarrow&\sum_{n=1}^{p}\dfrac{1}{n}\geq \dfrac{1}{p}+\ln p\end{array}$
Posons $S_{p}=\dfrac{1}{p}+\ln p$ alors, on a :
$$\sum_{n=1}^{p}\dfrac{1}{n}\geq S_{p}$$
Or, $\lim\limits_{p\rightarrow +\infty}S_{p}=\lim\limits_{p\rightarrow +\infty}\dfrac{1}{p}+\ln p=+\infty$ donc, en appliquant le théorème de comparaison, on obtient :
$$\boxed{\lim\limits_{p\rightarrow +\infty}\sum_{n=1}^{p}\dfrac{1}{n}=+\infty}$$
Partie B
1) Calculons pour tout $n\in\mathbb{N}^{\ast}$
$$\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t$$
a) En effectuant le changement de variable $u=t-n\pi$ et en remarquant que la fonction $u\mapsto|\sin u|$ est périodique de période $\pi$
Posons $u=t-n\pi$ donc, $\mathrm{d}t=\mathrm{d}u$
Ainsi :
\begin{eqnarray} \int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t&=&\int_{n\pi-n\pi}^{(n+1)\pi-n\pi}|\sin u+n\pi|\mathrm{d}u\nonumber\\ \nonumber\\&=&\int_{0}^{\pi}|\sin u+n\pi|\mathrm{d}u\quad\text{or, }\ |\sin u+n\pi|=|\sin u|\nonumber\\ \nonumber\\&=&\int_{0}^{\pi}|\sin u|\mathrm{d}u\quad\text{or, pour }u\in[0\;;\ \pi]\;,\ |\sin u|=\sin u\nonumber\\ \nonumber\\&=&\int_{0}^{\pi}\sin u\mathrm{d}u\nonumber\\ \nonumber\\&=&[-\cos u]_{0}^{\pi}\nonumber\\ \nonumber\\&=&-\cos\pi+\cos 0\nonumber\\ \nonumber\\&=&2\nonumber \end{eqnarray}
Donc,
$$\boxed{\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t=2}$$
b) En utilisant le résultat admis suivant :
$$\forall\;n\in\mathbb{N}\;,\ \forall\;t\in\;[n\pi\;,\ (n+1)\pi]\;,\ |\sin t|=(-1)^{n}\sin t$$
On obtient alors :
\begin{eqnarray} \int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t&=&\int_{n\pi}^{(n+1)\pi}(-1)^{n}\sin t\mathrm{d}t\nonumber\\ \nonumber\\&=&(-1)^{n}\int_{n\pi}^{(n+1)\pi}\sin t\mathrm{d}t\nonumber\\ \nonumber\\&=&(-1)^{n}[-\cos t]_{n\pi}^{(n+1)\pi}\nonumber\\ \nonumber\\&=&(-1)^{n}(-\cos(n+1)\pi+\cos n\pi)\nonumber\\ \nonumber\\&=&(-1)^{n}(-(-1)^{n+1}+(-1)^{n})\quad\text{or, }\ -(-1)^{n+1}=(-1)^{n+2}\nonumber\\ \nonumber\\&=&(-1)^{n}((-1)^{n+2}+(-1)^{n})\nonumber\\ \nonumber\\&=&(-1)^{2n+2}+(-1)^{2n}\nonumber\\ \nonumber\\&=&(-1)^{2(n+1)}+(-1)^{2n}\nonumber\\ \nonumber\\&=&1+1\nonumber\\ \nonumber\\&=&2\nonumber \end{eqnarray}
Ainsi,
$$\boxed{\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t=2}$$
2) Pour tout réel $a>0$, on considère la fonction $h_{a}$ définie sur $I=[0\;;\ +\infty[$ par :
$$h_{a}(t)=\left|\dfrac{\sin at}{t}\right|\;,\ \text{si }\;t\in\;]0\;;\ +\infty[\;,\text{ et }\;h_{a}(0)=a$$
a) Montrons que les fonctions $h_{a}$ sont continues sur $I.$
$\begin{array}{rcl}\lim_{t\rightarrow 0}h_{a}(t)&=&\lim_{t\rightarrow 0}\left|\dfrac{\sin at}{t}\right|\quad\text{posons }at=x\\ \\&=&\lim_{x\rightarrow 0}\left|\dfrac{\sin x}{\dfrac{x}{a}}\right|\\ \\&=&\lim_{x\rightarrow 0}\left|a\dfrac{\sin x}{x}\right|\\ \\&=&a\underbrace{\lim_{x\rightarrow 0}\left|\dfrac{\sin x}{x}\right|}_{=1}\\ \\&=&a\end{array}$
Ainsi, $\lim_{t\rightarrow 0}h_{a}(t)=h_{a}(0)=a$
D'où, les fonctions $h_{a}$ sont continues en 0.
Par conséquent, elles sont continues sur $I.$
b) Montrons que :
$$\forall\;n\in\mathbb{N}^{\ast}\ :\ \dfrac{1}{(n+1)\pi}\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\leq\dfrac{1}{n\pi}\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t$$
$$\text{et}\qquad \dfrac{1}{\pi}\int_{0}^{\pi}|\sin t|\mathrm{d}t\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t$$
Soit : $h_{1}(t)=\left|\dfrac{\sin t}{t}\right|$ alors, pour $t\in[n\pi\;,\ (n+1)\pi]$, on a :
$\begin{array}{rcrcccl} \forall\;n\in\mathbb{N}^{\ast}\;,\ n\pi\leq|t|\leq(n+1)\pi&\Leftrightarrow&\dfrac{1}{(n+1)\pi}&\leq&\dfrac{1}{t}&\leq&\dfrac{1}{n\pi}\\ \\&\Leftrightarrow&\dfrac{|\sin t|}{(n+1)\pi}&\leq&\dfrac{|\sin t|}{|t|} &\leq&\dfrac{|\sin t|}{n\pi}\\ \\&\Leftrightarrow&\dfrac{|\sin t|}{(n+1)\pi}&\leq&h_{1}(t)&\leq&\dfrac{|\sin t|}{n\pi}\end{array}$
Le passage à l'intégration donne :
$$\int_{n\pi}^{(n+1)\pi}\dfrac{|\sin t|}{(n+1)\pi}\mathrm{d}t\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\leq\int_{n\pi}^{(n+1)\pi}\dfrac{|\sin t|}{n\pi}\mathrm{d}t$$
Par suite,
$$\boxed{\forall\;n\in\mathbb{N}^{\ast}\ :\ \dfrac{1}{(n+1)\pi}\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\leq\dfrac{1}{n\pi}\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t}$$
De plus, sur $[0\;,\ \pi]$ on a :
$\begin{array}{rcccl} |t|\leq\pi&\Leftrightarrow&\dfrac{1}{\pi}&\leq&\dfrac{1}{|t|}\\ \\&\Leftrightarrow&\dfrac{|\sin t|}{\pi}&\leq&\dfrac{|\sin t|}{|t|}\\ \\&\Leftrightarrow&\dfrac{|\sin t|}{\pi}&\leq&h_{1}(t)\end{array}$
En intégrant, on obtient :
$$\int_{0}^{\pi}\dfrac{|\sin t|}{\pi}\mathrm{d}t\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t$$
D'où,
$$\boxed{\dfrac{1}{\pi}\int_{0}^{\pi}|\sin t|\mathrm{d}t\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t}$$
c) En déduisons que :
$$\forall\;n\in\mathbb{N}^{\ast}\ :\ \dfrac{2}{(n+1)\pi}\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\leq\dfrac{2}{n\pi}$$
(03)
$$\text{et}\qquad\dfrac{2}{\pi}\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t$$
On sait que :
$$\forall\;n\in\mathbb{N}^{\ast}\ :\ \dfrac{1}{(n+1)\pi}\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\leq\dfrac{1}{n\pi}\int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t$$
Or, d'après question 1), on a :
$$\forall\;n\in\mathbb{N}^{\ast}\;,\ \int_{n\pi}^{(n+1)\pi}|\sin t|\mathrm{d}t=2$$
Ce qui permet finalement d'écrire :
$$\boxed{\forall\;n\in\mathbb{N}^{\ast}\ :\ \dfrac{2}{(n+1)\pi}\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\leq\dfrac{2}{n\pi}}$$
De plus,
$$\dfrac{1}{\pi}\int_{0}^{\pi}|\sin t|\mathrm{d}t\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t$$
Or,
\begin{eqnarray} \int_{0}^{\pi}|\sin u|\mathrm{d}u&=&\int_{0}^{\pi}\sin u\mathrm{d}u\quad\text{car, sur }[0\;;\ \pi]\;,\ |\sin u|=\sin u\nonumber\\ \nonumber\\&=&[-\cos u]_{0}^{\pi}\nonumber\\ \nonumber\\&=&-\cos\pi+\cos 0\nonumber\\ \nonumber\\&=&2\nonumber \end{eqnarray}
D'où,
$$\boxed{\dfrac{2}{\pi}\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t}$$
3) On veut utiliser les résultats précédents pour calculer $$\lim_{a\rightarrow +\infty}\int_{0}^{\pi}h_{1}(t)\mathrm{d}t$$
a) Comparons
$$\dfrac{2}{\pi}\sum_{n=1}^{p}\dfrac{1}{n}\quad\text{et}\quad\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t$$
La relation (03) permet d'écrire :
$$\forall\;n\in\mathbb{N}^{\ast}\ :\ \dfrac{2}{(n+1)\pi}\leq\int_{n\pi}^{(n+1)\pi}h_{1}(t)\mathrm{d}t\qquad\text{et}\qquad\dfrac{2}{\pi}\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t$$
Ainsi,
\begin{eqnarray} \dfrac{2}{\pi}&\leq&\int_{0}^{\pi}h_{1}(t)\mathrm{d}t\nonumber\\ \nonumber\\\dfrac{2}{2\pi}&\leq&\int_{\pi}^{2\pi}h_{1}(t)\mathrm{d}t\nonumber\\ \nonumber\\\dfrac{2}{3\pi}&\leq&\int_{2\pi}^{3\pi}h_{1}(t)\mathrm{d}t\nonumber\\ \nonumber\\&\vdots&\nonumber\\ \nonumber\\ \dfrac{2}{p\pi}&\leq&\int_{(p-1)\pi}^{p\pi}h_{1}(t)\mathrm{d}t\nonumber \end{eqnarray}
En sommant membre à membre, on obtient :
$$\underbrace{\dfrac{2}{\pi}+\dfrac{2}{2\pi}+\dfrac{2}{3\pi}+\ldots+\dfrac{2}{p\pi}}_{\sum_{n=1}^{p}\frac{2}{n\pi}}\leq\int_{0}^{\pi}h_{1}(t)\mathrm{d}t+\int_{\pi}^{2\pi}h_{1}(t)\mathrm{d}t+\int_{2\pi}^{3\pi}h_{1}(t)\mathrm{d}t+\ldots+\int_{(p-1)\pi}^{p\pi}h_{1}(t)\mathrm{d}t$$
En appliquant la relation de Chasles, on obtient :
$$\int_{0}^{\pi}h_{1}(t)\mathrm{d}t+\int_{\pi}^{2\pi}h_{1}(t)\mathrm{d}t+\int_{2\pi}^{3\pi}h_{1}(t)\mathrm{d}t+\ldots+\int_{(p-1)\pi}^{p\pi}h_{1}(t)\mathrm{d}t=\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t$$
D'où,
$$\sum_{n=1}^{p}\dfrac{2}{n\pi}\leq\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t$$
Ce qui peut encore s'écrire
$$\boxed{\dfrac{2}{\pi}\sum_{n=1}^{p}\dfrac{1}{n}\leq\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t}$$
b) Déduisons
$$\lim_{p\rightarrow +\infty}\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t$$
D'après la question 4)b) partie A, on a :
$$\lim_{p\rightarrow +\infty}\sum_{n=1}^{p}\dfrac{1}{n}=+\infty$$
Donc, en appliquant le théorème de comparaison, on obtient :
$$\boxed{\lim_{p\rightarrow +\infty}\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t=+\infty}$$
c) Calculons
$$\lim_{x\rightarrow +\infty}\int_{0}^{x}h_{1}(t)\mathrm{d}t$$
Soit :
$$\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t$$
Posons $p=E\left(\dfrac{x}{\pi}\right)$; où $E$ désigne la fonction partie entière alors, on a :
$$\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t=\int_{0}^{E\left(\tfrac{x}{\pi}\right)\pi}h_{1}(t)\mathrm{d}t$$
Ainsi,
$$\lim_{p\rightarrow +\infty}\int_{0}^{p\pi}h_{1}(t)\mathrm{d}t=\lim_{x\rightarrow +\infty}\int_{0}^{E\left(\tfrac{x}{\pi}\right)\pi}h_{1}(t)\mathrm{d}t$$
Or, $E\left(\dfrac{x}{\pi}\right)\leq\dfrac{x}{\pi}\ \Rightarrow\ E\left(\dfrac{x}{\pi}\right)\pi\leq\dfrac{x}{\pi}\pi=x$
Donc, par conservation de l'ordre de l'intégration, on obtient :
$$\int_{0}^{E\left(\tfrac{x}{\pi}\right)\pi}h_{1}(t)\mathrm{d}t\leq\int_{0}^{\tfrac{x}{\pi}\pi}h_{1}(t)\mathrm{d}t$$
Par suite,
$$\int_{0}^{E\left(\tfrac{x}{\pi}\right)\pi}h_{1}(t)\mathrm{d}t\leq\int_{0}^{x}h_{1}(t)\mathrm{d}t$$
D'où,
$$\lim_{x\rightarrow +\infty}\int_{0}^{x}h_{1}(t)\mathrm{d}t\geq\lim_{x\rightarrow +\infty}\int_{0}^{E\left(\tfrac{x}{\pi}\right)\pi}h_{1}(t)\mathrm{d}t=+\infty$$
Par conséquent,
$$\boxed{\lim_{x\rightarrow +\infty}\int_{0}^{x}h_{1}(t)\mathrm{d}t=+\infty}$$
4) Montrons que
$$\forall\;a\in\mathbb{R}_{+}^{\ast}\ :\ \int_{0}^{\pi}h_{a}(t)\mathrm{d}t=\int_{0}^{a\pi}h_{1}(t)\mathrm{d}t$$
Soit $a>0$ alors,
$$\int_{0}^{\pi}h_{a}(t)\mathrm{d}t=\int_{0}^{\pi}\left|\dfrac{\sin at}{t}\right|\mathrm{d}t$$
Effectuons un changement de variable Soit : $u=at$ alors, $\mathrm{d}u=a\mathrm{d}t$
Ainsi,
\begin{eqnarray}\int_{0}^{\pi}\left|\dfrac{\sin at}{t}\right|\mathrm{d}t&=&\int_{0}^{a\pi}\left|\dfrac{\sin u}{\dfrac{u}{a}}\right|\dfrac{\mathrm{d}u}{a}\nonumber\\ \nonumber\\&=&\int_{0}^{a\pi}a\left|\dfrac{\sin u}{u}\right|\dfrac{\mathrm{d}u}{a}\nonumber\\ \nonumber\\&=&\int_{0}^{a\pi}\left|\dfrac{\sin u}{u}\right|\mathrm{d}u \nonumber \end{eqnarray}
Par suite,
$$\int_{0}^{\pi}\left|\dfrac{\sin at}{t}\right|\mathrm{d}t=\int_{0}^{a\pi}\left|\dfrac{\sin t}{t}\right|\mathrm{d}t=\int_{0}^{a\pi}h_{1}(t)\mathrm{d}t$$
$a$ étant quelconque dans $\mathbb{R}_{+}^{\ast}$ donc,
$$\boxed{\forall\;a\in\mathbb{R}_{+}^{\ast}\ :\ \int_{0}^{\pi}h_{a}(t)\mathrm{d}t=\int_{0}^{a\pi}h_{1}(t)\mathrm{d}t}$$
En déduisons $$\lim_{a\rightarrow +\infty}\int_{0}^{\pi}h_{a}(t)\mathrm{d}t$$
Comme $\int_{0}^{\pi}h_{a}(t)\mathrm{d}t=\int_{0}^{a\pi}h_{1}(t)\mathrm{d}t$ alors,
$$\lim_{a\rightarrow +\infty}\int_{0}^{\pi}h_{a}(t)\mathrm{d}t=\lim_{a\rightarrow +\infty}\int_{0}^{a\pi}h_{1}(t)\mathrm{d}t$$
Or, en posant $x=a\pi$, on obtient :
$$\lim_{a\rightarrow +\infty}\int_{0}^{a\pi}h_{1}(t)\mathrm{d}t=\lim_{x\rightarrow +\infty}\int_{0}^{x}h_{1}(t)\mathrm{d}t$$
Et d'après la question 3)c)
$$\lim_{x\rightarrow +\infty}\int_{0}^{x}h_{1}(t)\mathrm{d}t=+\infty$$
Par conséquent,
$$\boxed{\lim_{a\rightarrow +\infty}\int_{0}^{\pi}h_{a}(t)\mathrm{d}t=+\infty}$$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
sam, 04/24/2021 - 05:40
Permalien
Télécharger
azer (non vérifié)
sam, 01/08/2022 - 01:16
Permalien
bon document
Ajouter un commentaire