Suites numériques - T S

$\centerdot\ \ $ Une suite $(u_{n})_{n\in I}\;,\ I\subset\mathbb{N}$ est une application de $I$ dans $\mathbb{R}$ $$\begin{eqnarray} u\ :\ I\subset\mathbb{N}&\longrightarrow&\mathbb{R}\nonumber \\ n&\longrightarrow&u(n)=u_{n}\nonumber \end{eqnarray}$$

$\centerdot\ \ $ Elle peut être définie de façon explicite

$u_{n}=2n^{2}+1\;,\quad v_{n}=\dfrac{n^{2}-4}{2n}\;;\ n\in\mathbb{N}^{*}$

 

$\centerdot\ \ $ Elle peut être aussi définie par la donnée d'un terme et d'une relation dite de récurrence liant des termes.

$$\left\lbrace\begin{array}{rcl} u_{0}&=&\alpha \\ u_{n+1}&=&2u_{n}-3\end{array}\right.\;,\quad\left\lbrace\begin{array}{rcl} v_{1}&=&\alpha \\ v_{n+1}&=&f(v_{n})\end{array}\right.$$

$f$ est la fonction associée à la suite $(v_{n})$

Pour démontrer par récurrence qu'une propriété $p_{n}$ est vraie $\forall\;n\geq n_{0}$ on doit :

 

$-\ $ montrer que la propriété est vraie au premier rang ($p_{n_{0}}$ vraie)

 

$-\ $ supposer que la propriété est vraie jusqu'au rang $n$ ($p_{n}$ vraie) et démontrer qu'elle est vraie au rang $n+1$

 

$-\ $ et enfin conclure

Montrer que $$\forall\;n\geq 1\;,\ 1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}=\dfrac{n(n+1)(2n+1)}{6}$$

Soit la propriété suivante : $$\forall\;n\geq 1\;,\ \underbrace{1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}}_{A_{n}}=\underbrace{\dfrac{n(n+1)(2n+1)}{6}}_{B_{n}}$$

 

$-$ Montrons que la propriété est vraie pour $n=1$

 

$n=1$ alors $A_{1}=1^{2}=1$ et $B_{1}=\dfrac{1(1+1)(2+1)}{6}=\dfrac{6}{6}=1$

 

$A_{1}=B_{1}$ donc la propriété est vraie au 1er rang.

 

$-$ Supposons que la proposition est vraie jusqu'au rang $n$, donc 

 

$\forall\;n\geq 1\;,\ 1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}=\dfrac{n(n+1)(2n+1)}{6}$ et montrons qu'elle est vraie au rang $n+1.$

 

C'est-à-dire $1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}+(n+1)^{2}=\dfrac{(n+1)(n+2)(2n+3)}{6}.$

 

On a :

 

$\begin{array}{rcl} 1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}+(n+1)^{2}&=&\dfrac{n(n+1)(2n+1)}{6}+(n+1)^{2}\\ \\ &=&\dfrac{n(n+1)(2n+1)+6(n+1)^{2}}{6}\\ \\ &=&\dfrac{(n+1)(2n^{2}+n+6n+6)}{6}\\ \\ &=&\dfrac{(n+1)(2n^{2}+7n+6)}{6}\end{array}$

 

Or, $2n^{2}+7n+6=(n+2)(2n+3)$, donc 

 

$1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}+(n+1)^{2}=\dfrac{(n+1)(n+2)(2n+3)}{6}.$

 

Ainsi, la proposition est vraie au rang $n+1$

 

Donc $\forall\;n\geq 1\;,\ 1^{2}+2^{2}+3^{2}+\ldots\ldots+n^{2}=\dfrac{n(n+1)(2n+1)}{6}$

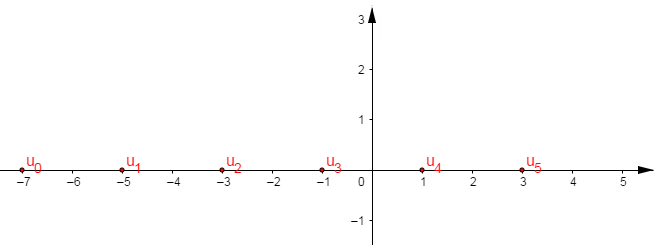
$-\ $ Si $u_{n}$ est définie de façon explicite ; $u_{n}=f(n)$ alors représenter graphiquement la suite $(u_{n})$ consiste à représenter dans un repère l'ensemble des points isolés $(n\;,\ u_{n}).$

 

$-\ $ On peut aussi représenter directement les valeurs des termes de la suite sur l'un des axes du repère.

Représenter les 6 premiers termes de la suite $(u_{n})$ définie par :

 

a) $u_{n}=\dfrac{n^{2}+1}{2n+3}$ 

 

b) $u_{n}=2n-7$

a) 

 

b) 

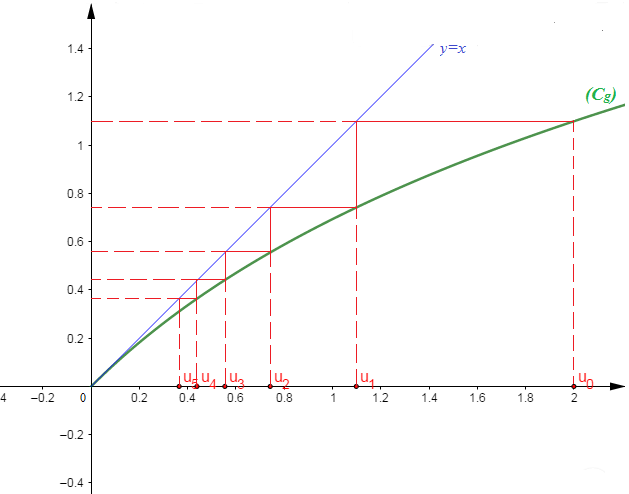
$-\ $ Si $u_{n}$ est définie de façon récurrente ; $\left\lbrace\begin{array}{rcl} u_{0}&=&\alpha \\ u_{n+1}&=&g(u_{n})\end{array}\right.\;,\ g$ étant la fonction associée à la suite $(u_{n})$, alors on trace la courbe de $g$ et la première bissectrice (droite d'équation $y=x$). Par projection, on construit les termes de la suite $(u_{n})$ en procédant comme suit :

 

(1) On place le premier terme $u_{0}$ sur l'axe des abscisses ;

 

(2) On utilise $C_{g}$ pour construire $u_{1}=g(u_{0})$ sur l'axe des ordonnées ;

 

(3) On projette $u_{1}$ sur l'axe des abscisses à l'aide de la première bissectrice ;

 

(4) On répète la même procédure en utilisant à nouveau $C_{g}$ pour construire $u_{2}=g(u_{1})$ sur l'axe des ordonnées ;

 

(5) On projette ensuite $u_{2}$ sur l'axe des abscisses à l'aide de la première bissectrice ;

 

(6) etc...

Représenter les 6 premiers termes de la suite $(u_{n})$ définie par $$\left\lbrace\begin{array}{rcl} u_{0}&=&2 \\ u_{n+1}&=&\ln(1+u_{n})\;,\ \forall\;n\in\mathbb{N}\end{array}\right.$$

$\centerdot\ \ (u_{n})_{n\in I}$ est majorée si, et seulement si, il existe $M\in\mathbb{R}$ tel que $$\forall\;n\in I\;,\ u_{n}\leq M$$

 

$\centerdot\ \ (u_{n})_{n\in I}$ est minorée si, et seulement si, il existe $m\in\mathbb{R}$ tel que $$\forall\;n\in I\;,\ u_{n}\geq m$$

 

$\centerdot\ \ (u_{n})_{n\in I}$ est bornée si, et seulement si, il existe $m\;,\ M\in\mathbb{R}$ tels que $$\forall\;n\in I\;,\ m\leq u_{n}\leq M\quad\text{ou}\quad \exists\;k>0\;,\ \forall\;n\in I\;,\ |u_{n}|\leq k$$

$\centerdot\ \ (u_{n})_{n\in I}$ est croissante si, et seulement si, $$\forall\;n\in I\;,\ u_{n+1}\geq u_{n}$$

 

$\centerdot\ \ (u_{n})_{n\in I}$ est décroissante si, et seulement si, $$\forall\;n\in I\;,\ u_{n+1}\leq u_{n}$$

 

$\centerdot\ \ (u_{n})_{n\in I}$ est constante si, et seulement si, $$\forall\;n\in I\;,\ u_{n+1}=u_{n}$$

 

$\centerdot\ \ (u_{n})_{n\in I}$ est stationnaire si, et seulement si $\exists\;p\in\mathbb{N}$ tel que $$\forall\;n\geq p\;,\ u_{n}=u_{p}$$

 

$\centerdot\ \ (u_{n})_{n\in I}$ est périodique de période $T\in\mathbb{R}$ si, et seulement si $$\forall\;n\in I\;,\ u_{n+T}=u_{n}$$

On dit que la suite $(u_{n})_{n\in I}$ est monotone sur $I$ si $\forall\;n\in I$ elle est croissante ou décroissante.

Dans chacun des cas suivants, étudier la monotonie de la suite $(u_{n})$

 

a) $\forall\;n\in\mathbb{N}\;,\  u_{n}=\dfrac{n^{2}}{n+1}$

 

b) $\forall\;n\in\mathbb{N}^{*}\;,\  u_{n}=n^{n}$

a) Soit $f$ la fonction définie sur $\mathbb{R}_{+}$ telle que $u_{n}=f(n)$ avec : $$f(x)=\dfrac{x^{2}}{x+1}$$

Cette fonction $f$ est rationnelle, définie et dérivable sur $\mathbb{R}_{+}$,

 

$\begin{array}{rcl} f'(x)&=&\dfrac{2x(x+1)-x^{2}}{(x+1)^{2}}\\ \\ &=&\dfrac{2x^{2}+2x-x^{2}}{(x+1)^{2}}\\ \\ &=&\dfrac{x^{2}+2x}{(x+1)^{2}}\\ \\ &=&\dfrac{x(x+2)}{(x+1)^{2}}\end{array}$

 

$f'(x)$ a le même signe que $x(x+2)$ lequel est positif sur $]-\infty\;,\ -2]\cup[0\;,\ +\infty[.$

 

Donc, pour $x\in\mathbb{R}_{+}\;,\ f'(x)\geq 0$, par suite la fonction $f$ est croissante sur $[0\;,\ +\infty[$ sa restriction à $\mathbb{N}$ est croissante.

 

Donc la suite $(u_{n})$ est croissante pour tout entier naturel.

 

b) Ici on peut comparer les rapports entre $u_{n+1}$ et $u_{n}$. On a :

 

$\begin{array}{rcl} \dfrac{u_{n+1}}{u_{n}}&=&\dfrac{(n+1)^{(n+1)}}{n^{n}}\\ \\ &=&\left(\dfrac{n+1}{n}\right)^{n}(n+1)\\ \\ &=&\left(1+\dfrac{1}{n}\right)^{n}(n+1)\quad\text{(supérieure à }1)\end{array}$

 

Donc $\dfrac{u_{n+1}}{u_{n}}>1\ \Rightarrow\ u_{n+1}>u_{n}\;;\quad\forall\;n\in\mathbb{N}^{*}.$ 

 

D'où la suite $(u_{n})$ est strictement croissante pour tout entier naturel non nul.

$(u_{n})_{n\in\mathbb{N}}$ est une suite arithmétique si, et seulement si, il existe un réel $r\in\mathbb{R}^{*}$ tel que $$u_{n+1}-u_{n}=r$$

$r$ est appelé raison de la suite $(u_{n})_{n\in\mathbb{N}}$.

$\centerdot\ \ $ Relation entre $u_{n}\;,\ u_{p}$ et $r$

 

Soit $p\in\mathbb{N}\;;\ p\leq n$, alors on a : $$u_{n}=u_{p}+(n-p)r$$

$\centerdot\ \ $ Relation entre trois termes consécutifs $a\;,\ b$ et $c$

 

Soit $a\;,\ b$ et $c$ trois termes consécutifs alors $b=\dfrac{a+c}{2}$, donc $$u_{n+1}=\dfrac{u_{n}+u_{n+2}}{2}$$

$\centerdot\ \ $ Somme de termes consécutifs

$$s_{n}=\sum_{k=p}^{n}u_{k}=u_{p}+u_{p+1}+\ldots\ldots+u_{n}=\dfrac{(n-p+1)(u_{p}+u_{n})}{2}$$

Les suites suivantes sont-elles arithmétiques ?

 

a) $u_{n}=2n+1$

 

b) $u_{n}=\dfrac{n^{2}}{2}$

a)

$\begin{array}{rcl} u_{n+1}-u_{n}&=&2(n+1)+1-2n-1\\ \\ &=&2n+2+1-2n-1\\ \\ &=&2\quad\text{(constante)}\end{array}$

 

Donc $(u_{n})$ est une suite arithmétique de raison $r=2$

 

b)

$\begin{array}{rcl} u_{n+1}-u_{n}&=&\dfrac{(n+1)^{2}}{2}-\dfrac{n^{2}}{2}\\ \\ &=&\dfrac{n^{2}+2n+1-n^{2}}{2}\\ \\ &=&\dfrac{2n+1}{2}\end{array}$

 

On constate que la quantité $u_{n+1}-u_{n}$ dépend de $n$ donc la suite $(u_{n})$ n'est pas une suite arithmétique.

$(v_{n})_{n\in\mathbb{N}}$ est une suite géométrique si, et seulement si, il existe un réel 

 

$q\in\mathbb{R}^{*}\setminus\{1\}$ tel que $$v_{n+1}=qv_{n}$$

$q$ est appelé raison de la suite $(v_{n})_{n\in\mathbb{N}}$.

$\centerdot\ \ $ Relation entre $v_{n}\;,\ v_{p}$ et $q$

 

Soit $p\in\mathbb{N}\;;\ p\leq n$, alors on a : $$v_{n}=q^{n-p}v_{p}$$

$\centerdot\ \ $ Relation entre trois termes consécutifs $a\;,\ b$ et $c$

 

Soit $a\;,\ b$ et $c$ trois termes consécutifs alors $b^{2}=ac$, donc $$v_{n+1}^{2}=v_{n}v_{n+2}$$

$\centerdot\ \ $ Somme de termes consécutifs

$$s_{n}=\sum_{k=p}^{n}v_{k}=v_{p}+v_{p+1}+\ldots\ldots+v_{n}=v_{p}\dfrac{(1-q^{n-p+1})}{1-q}$$

$\centerdot\ \ \lim\limits_{n\rightarrow+\infty}q^{n}=\left\lbrace\begin{array}{rcl} +\infty&\text{si}&q>1\ \text{ (suite croissante)} \\ 1&\text{si}&q=1\ \text{ (suite constante)} \\ 0&\text{si}&-1<q<0\ \text{ (suite alternée)} \\ 0&\text{si}&0<q<1\ \text{ (suite décroissante)} \\ \text{n'existe pas}&\text{si}&q\leq -1\ \text{ (suite alternée)}\end{array}\right.$

Les suites suivantes sont-elles géométriques ?

 

a) $v_{n}=2n$

 

b) $v_{n}=3\left(\dfrac{1}{2}\right)^{n}$

a)

$\begin{array}{rcl} \dfrac{v_{n+1}}{v_{n}}&=&\dfrac{2(n+1)}{2n}\\ \\ &=&\dfrac{n+1}{n}\end{array}$

 

On remarque que le rapport $\dfrac{v_{n+1}}{v_{n}}$ n'est pas une constante donc $(v_{n})$ n'est pas une suite géométrique.

 

b)

$\begin{array}{rcl} \dfrac{v_{n+1}}{v_{n}}&=&\dfrac{3\left(\dfrac{1}{2}\right)^{n+1}}{3\left(\dfrac{1}{2}\right)^{n}}\\ \\ &=&\left(\dfrac{1}{2}\right)^{n+1-n}\\ \\ &=&\dfrac{1}{2}\quad\text{(constante)}\end{array}$

 

Donc $(v_{n})$ est une suite géométrique de raison $q=\dfrac{1}{2}$

$\centerdot\ \ (u_{n})_{n\in\mathbb{N}}$ est convergente si, et seulement si, $$\lim_{n\rightarrow+\infty}u_{n}\ \text{ existe }\ =\ell\in\mathbb{R}$$

On dira que $(u_{n})_{n\in\mathbb{N}}$ converge vers $\ell$

 

$\centerdot\ \ $ On peut aussi écrire $$\lim_{n\rightarrow+\infty}u_{n}=\ell\ \Leftrightarrow\ \forall\;\varepsilon\in\mathbb{R}_{+}\;,\ \exists\;n_{0}\in\mathbb{N}\ \text{ tels que }\ \forall\;n\geq n_{0}\;;\ |u_{n}-\ell|\leq\varepsilon$$

$\centerdot\ \ $ On dit que $(u_{n})_{n\in\mathbb{N}}$ diverge si $u_{n}$ n'a pas de limite ou si sa limite est infinie.

$\centerdot\ \ $ Toute suite croissante et majorée converge.

 

$\centerdot\ \ $ Toute suite décroissante et minorée converge.

 

$\centerdot\ \ $ Toute suite convergente est bornée (réciproque fausse).

 

$\centerdot\ \ $ Si une suite converge, alors sa limite est unique.

 

$\centerdot\ \ $ Soit une suite $(u_{n})$ définie par $u_{n}=f(n)$ avec $f$ définie sur un intervalle $I$ de $\mathbb{R}$, alors $$\text{si }\ \lim f=\ell\;,\ \text{ alors }\ \lim u_{n}=\ell$$

Soient $(u_{n})\ $ et $\ (v_{n})$ deux suites numériques convergentes telles que $\lim u_{n}=\ell\ $ et $\ \lim v_{n}=\ell'$, alors

 

$\centerdot\ \ (u_{n}+v_{n})$ converge et $\lim (u_{n}+v_{n})=\lim u_{n}+\lim u_{n}=\ell+\ell'$

 

$\centerdot\ \ (u_{n}v_{n})$ converge et $\lim (u_{n}v_{n})=\lim u_{n}\times\lim v_{n}=\ell\ell'$

 

$\centerdot\ \ \left(\dfrac{u_{n}}{v_{n}}\right)$ converge et $\lim\dfrac{u_{n}}{v_{n}}=\dfrac{\lim u_{n}}{\lim v_{n}} =\dfrac{\ell}{\ell'}\;;\quad \ell'\neq 0$

 

$\centerdot\ \ $ Théorèmes de comparaison 

 

$-\ $ Soit $(u_{n})$ et $(v_{n})$ deux suites numériques et $n_{0}\in\mathbb{N}$ tel que 

 

$\forall\;n\geq n_{0}\;,\ u_{n}\leq v_{n}\ $, si $\ \lim u_{n}=\ell$ et $\lim v_{n}=\ell'$ alors, $\ell\leq\ell'$

 

$-\ $ Si $\lim v_{n}=-\infty$ alors, $\lim u_{n}=-\infty$

 

$-\ $ Si $\lim u_{n}=+\infty$ alors, $\lim v_{n}=+\infty$

 

$-\ $ Si $|u_{n}|\leq v_{n}\ $ et $\ \lim v_{n}=0$ alors, $\lim u_{n}=0$

Déterminer la limite de la suite $(u_{n})_{n\in\mathbb{N}^{*}}$ définie par :

 

a) $u_{n}=\dfrac{\cos n}{n}$

 

b) $u_{n}=\sum_{p=1}^{n}\dfrac{1}{\sqrt{p}}=1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+\ldots\ldots+\dfrac{1}{\sqrt{n}}$

a)

$\begin{array}{rcl} \forall\;n\in\mathbb{N}^{*}\;,\;\ |u_{n}|&=&\left|\dfrac{\cos n}{n}\right|\\ \\ &=&\dfrac{|\cos n|}{n}\\ \\&\leq&\dfrac{1}{n}\quad\text{car pour tout réel }x\;,\ |\cos x|\leq 1\end{array}$

 

Donc $\forall\;n\in\mathbb{N}^{*}\;,\;\ |u_{n}|\leq\dfrac{1}{n}$.

 

Posons $v_{n}=\dfrac{1}{n}$ alors, $\lim\limits_{n\rightarrow+\infty}v_{n}=\lim\limits_{n\rightarrow+\infty}\dfrac{1}{n}=0.$

 

Donc $\lim\limits_{n\rightarrow+\infty}u_{n}=0$

 

b)

$\begin{array}{rcl} \text{Soit }1\leq p\leq n\;,&\text{alors}&1\leq\sqrt{p}\leq\sqrt{n}\\ \\ &\Rightarrow&\dfrac{1}{\sqrt{n}}\leq\dfrac{1}{\sqrt{p}}\leq 1\end{array}$

 

Donc

 

$\begin{array}{rcl} \dfrac{1}{\sqrt{n}}\leq &\dfrac{1}{\sqrt{1}}&\leq 1\\ \\ \dfrac{1}{\sqrt{n}}\leq&\dfrac{1}{\sqrt{2}}&\leq 1\\ \\ \dfrac{1}{\sqrt{n}}\leq&\dfrac{1}{\sqrt{3}}&\leq 1\\ \\ \vdots&\vdots&\vdots\\ \\ \dfrac{1}{\sqrt{n}}\leq&\dfrac{1}{\sqrt{n}}&\leq 1\end{array}$

En sommant ces inégalités membre à membre on obtient : 

 

$\underbrace{\dfrac{1}{\sqrt{n}}+\dfrac{1}{\sqrt{n}}+\ldots+\dfrac{1}{\sqrt{n}}}_{n\text{ fois}}\leq 1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+\ldots+\dfrac{1}{\sqrt{n}}\leq\underbrace{1+1+\ldots\ldots+1}_{n\text{ fois}}$ 

 

Donc $\dfrac{n}{\sqrt{n}}\leq u_{n}\leq n\ \Leftrightarrow\ \sqrt{n}\leq u_{n}\leq n$

 

Posons $v_{n}=\sqrt{n}$, alors $\forall\;n\in\mathbb{N}^{*}\;,\ u_{n}\geq v_{n}$.

 

Or, $\lim\limits_{n\rightarrow+\infty}v_{n}=\lim\limits_{n\rightarrow+\infty}\sqrt{n}=+\infty.$

 

Donc $\lim\limits_{n\rightarrow+\infty}u_{n}=+\infty$

 

$\centerdot\ \ $ Théorème des gendarmes 

 

$-\ $ Soit $(u_{n})\;,\ (v_{n})$ et $(w_{n})$ trois suites numériques telles que 

 

$\lim u_{n}=\lim w_{n}=\ell.$ S'il existe $n_{0}\in\mathbb{N}\;;\ \forall\;n\geq n_{0}\;,\ u_{n}\leq v_{n}\leq w_{n}$, alors $\lim v_{n}=\ell.$

 

$-\ $ Si $|u_{n}-\ell|\leq v_{n}\ $ et $\ \lim v_{n}=0$ alors, $\lim u_{n}=\ell$

Déterminer la limite de la suite $(u_{n})_{n\in\mathbb{N}}$ définie par 

 

$u_{n}=\dfrac{1}{n^{2}+1}+\dfrac{1}{n^{2}+2}+\ldots\ldots+\dfrac{1}{n^{2}+n}$

 

$\forall\;p\in\{1\;,\ 2\;,\ \ldots\;,\ n\}\;;\ n^{2}+1\leq n^{2}+p\leq n^{2}+n$, alors $$\dfrac{1}{n^{2}+n}\leq\dfrac{1}{n^{2}+p}\leq\dfrac{1}{n^{2}+1}$$

Donc $$\begin{eqnarray} \dfrac{1}{n^{2}+n}\leq &\dfrac{1}{n^{2}+1}&\leq\dfrac{1}{n^{2}+1}\nonumber \\ \dfrac{1}{n^{2}+n}\leq&\dfrac{1}{n^{2}+2}&\leq\dfrac{1}{n^{2}+1}\nonumber \\ \dfrac{1}{n^{2}+n}\leq&\dfrac{1}{n^{2}+3}&\leq\dfrac{1}{n^{2}+1}\nonumber \\ \vdots&\vdots&\vdots\nonumber \\ \dfrac{1}{n^{2}+n}\leq&\dfrac{1}{n^{2}+n}&\leq\dfrac{1}{n^{2}+1}\nonumber \end{eqnarray}$$

En sommant ces inégalités membre à membre on obtient : 

 

$\underbrace{\dfrac{1}{n^{2}+n}+\dfrac{1}{n^{2}+n}+\ldots+\dfrac{1}{n^{2}+n}}_{n\text{ fois}}\leq u_{n}\leq\underbrace{\dfrac{1}{n^{2}+1}+\dfrac{1}{n^{2}+1}+\ldots\ldots+\dfrac{1}{n^{2}+1}}_{n\text{ fois}}$ 

 

Donc $\dfrac{n}{n^{2}+n}\leq u_{n}\leq\dfrac{n}{n^{2}+1}$

 

Posons $v_{n}=\dfrac{n}{n^{2}+n}\ $ et $\ w_{n}=\dfrac{n}{n^{2}+1}$, alors $\forall\;n\in\mathbb{N}\;,\ v_{n}\leq u_{n}\leq w_{n}.$

 

Or, $\left\lbrace\begin{array}{rcl} \lim\limits_{n\rightarrow+\infty}v_{n}&=&\lim\limits_{n\rightarrow+\infty}\dfrac{n}{n^{2}+n}\ =\ 0 \\ \\ \lim\limits_{n\rightarrow+\infty}w_{n}&=&\lim\limits_{n\rightarrow+\infty}\dfrac{n}{n^{2}+1}\ =\ 0\end{array}\right.$

 

Donc, $\lim\limits_{n\rightarrow+\infty}u_{n}=0$

Soit $(u_{n})$ la suite définie par $\left\lbrace\begin{array}{rcl} u_{0}&=&\alpha \\ u_{n+1}&=&f(u_{n})\end{array}\right.\;,\ f$ est la fonction associée à la suite $(u_{n})$

Soit $f$ une fonction continue sur un intervalle $I$ de $\mathbb{R}$, si 

 

$-\ \forall\;n\;,\ u_{n}\in I$

 

$-\ (u_{n})$ converge vers $\ell$ 

 

alors $\ell$ est solution de l'équation $f(x)=x$  

Soit $(u_{n})$ la suite définie par $\left\lbrace\begin{array}{rcl} u_{0}&=&1 \\ u_{n+1}&=&\sqrt{2+u_{n}}\end{array}\right.$ telle que pour tout entier naturel $n\;,\ 1\leq u_{n}\leq 2$

 

1) Montrer que la suite $(u_{n})$ est croissante.

 

2) En déduire que $(u_{n})$ est convergente et calculer sa limite 

1)

 

$\begin{array}{rcl} u_{n+1}-u_{n}&=&\sqrt{2+u_{n}}-u_{n}\\ \\ &=&\dfrac{(\sqrt{2+u_{n}}-u_{n})(\sqrt{2+u_{n}}+u_{n})}{\sqrt{2+u_{n}}+u_{n}}\\ \\ &=&\dfrac{2+u_{n}-u_{n}^{2}}{\sqrt{2+u_{n}}+u_{n}}\\ \\ &=&\dfrac{-(u_{n}-2)(u_{n}+1)}{\sqrt{2+u_{n}}+u_{n}}\geq 0\quad \text{car }u_{n}-2\leq 0\end{array}$

 

Donc $u_{n+1}\geq u_{n}$, d'où $(u_{n})$ est croissante.

 

2) La suite $(u_{n})$ est croissante et majorée par 2 donc elle est convergente.

 

$u_{n+1}=f(u_{n})$ avec $f\ :\ x\mapsto\ \sqrt{2+x}$

 

$(u_{n})$ converge vers $\ell\ $ et $\ f$ continue sur $[-2\;,\ +\infty[$ en particulier sur $I=[1\;,\ 2]$ 

 

$\forall\;n\;,\ u_{n}\in I$ donc $\ell\in I.$

 

Donc $\ell$ est solution de l'équation $f(x)=x$. On a :

 

$\begin{array}{rcl} f(\ell)=\ell&\Leftrightarrow&\sqrt{2+\ell}=\ell\\ \\ &\Leftrightarrow&\ell^{2}=2+\ell\\ \\ &\Leftrightarrow&\ell^{2}-\ell-2=0\\ \\ &\Leftrightarrow&\ell=2\ \text{ ou }\ \ell=-1\end{array}$

 

La solution positive de l'équation $\ell^{2}-\ell-2=0$ est 2, donc $\lim u_{n}=2.$

Deux suites $(u_{n})$ et $(v_{n})$ sont adjacentes si les trois conditions suivantes sont vérifiées :

 

$-\ $ Pour tout entier naturel $n\in I\;,\ u_{n}\leq v_{n}$

 

$-\ \ (u_{n})$ croissante et $(v_{n})$ décroissante

 

$-\ \ \lim(v_{n}-u_{n})=0$

Deux suites adjacentes convergent vers la même limite.