Corrigé devoir n° 2 maths - 6e

Classe: 
Sixième
 

Exercice 1

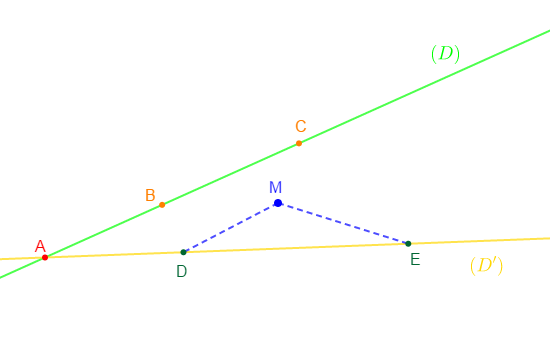
Soit A  et  M deux points du plan et (D)  et  (D′) deux droites sécantes en A.
 
1) Plaçons deux ponts B  et  C sur la droite (D) tels que : BC=3cm
 
2) Plaçons deux ponts D  et  E sur la droite (D′) tels que : DE=4.5cm
 
3) Comparons les mesures des segments [BC]  et  [DE]
 
On a : BC=3cm  et  DE=4.5cm
 
Or, 4.5cm est supérieur à 3cm donc,
DE>BC
4) Montrons que MD+ME>BC
 
Comme M∉[DE] alors, d'après l'inégalité triangulaire, on a :
MD+ME>DE
Or, à la question 3), on a : DE>BC
 
Donc,
MD+ME>DE  et  DE>BC
Par conséquent,
MD+ME>BC
 

Exercice 2

1) Complétons les pointillés par ∈  ou  ∉.
 
7∈N;15.0∈D;8.01∈D
 
1∈N;0∈D;10.1∈D
 
15.4∉N;0.00001∈D;1.01∉N
 
2) Complétons les pointillés par ⊂  ou \ \not\subset.
 
\{0\;;\ 3.5\;;\ 2\;;\ 0.9\;;\ 45\;;\ 7\}\not\subset\mathbb{N}
 
\{0\;;\ 3.5\;;\ 2\;;\ 0.9\;;\ 45\;;\ 7\}\subset\mathfrak{D}
 
\mathfrak{D}\not\subset\mathbb{N}
 
\{2.3\;;\ 9\;;\ 12\}\subset\{0.01\;;\ 35\;;\ 12\;;\ 32\;;\ 9\;;\ 945\;;\ 2.3\}

Exercice 3

Fatoumata, Ramatoulaye, Amadou et Oumy sont tous de la classe de 6^{em}\;B. 
 
1) Écrivons l'ensemble G des lettres utilisés pour écrire le nom de Amadou, 
 
G=\{a\;;\ m\;;\ d\;;\ o\;;\ u\}
 
2) Écrivons l'ensemble H des lettres utilisés pour écrire le nom de Fatoumata
 
H=\{f\;;\ a\;;\ t\;;\ o\;;\ u\;;\ m\}
 
3) Écrivons l'ensemble V des lettres utilisés pour écrire le nom de Ramatoulaye.
 
V=\{r\;;\ a\;;\ m\;;\ t\;;\ o\;;\ u\;;\ l\;;\ y\;;\ e\}
 
4) Déterminons G\cap H\;,\quad G\cap V\;,\quad\ et \ G\cap H\cap V
 
G\cap H=\{a\;;\ m\;;\ o\;;\ u\}
 
G\cap V=\{a\;;\ m\;;\ o\;;\ u\}
 
G\cap H\cap V=\{a\;;\ m\;;\ o\;;\ u\}
 
5) Déterminer G\cup V\;,\quad V\cup H\;,\quad G\cup H\ et \ G\cup H\cup V
 
G\cup V=\{a\;;\ m\;;\ d\;;\ o\;;\ u\;;\ r\;;\ t\;;\ l\;;\ y\;;\ e\}
 
V\cup H=\{r\;;\ a\;;\ m\;;\ t\;;\ o\;;\ u\;;\ l\;;\ y\;;\ e\;;\ f\}
 
G\cup H=\{a\;;\ m\;;\ d\;;\ o\;;\ u\;;\ f\;;\ t\}
 
G\cup H\cup V=\{a\;;\ m\;;\ d\;;\ o\;;\ u\;;\ f\;;\ t\;;\ r\;;\ l\;;\ y\;;\ e\}
 
6) Écrivons l'ensemble W des lettres utilisés pour écrire le nom de Oumy.
 
W=\{o\;;\ u\;;\ m\;;\ y\}
 
7) Montrons que W\cap V=W
 
On constate que tous les éléments de l'ensemble W appartiennent à l'ensemble V.
 
Donc, W\subset V
 
Par conséquent, W\cap V=W
 
Vérification : W\cap V=\{o\;;\ u\;;\ m\;;\ y\}=W

 

Auteur: 
Diny Faye

Commentaires

Ousmane Niasse (non vérifié)

sam, 03/19/2022 - 20:38

Fait des exercices particulier

becaye diop (non vérifié)

mer, 10/19/2022 - 22:57

vous avez changer les notations de l exercice 3 du devoir

khadydia (non vérifié)

mer, 02/01/2023 - 21:43

Mercie de nous edais

Anonyme (non vérifié)

jeu, 11/30/2023 - 01:20

Merci

Adama Souare (non vérifié)

mer, 06/05/2024 - 22:23

Je veux être plusieurs forte en maths

Anonyme (non vérifié)

lun, 12/16/2024 - 22:19

Ccccccc Uytrr

Ajouter un commentaire