Solution des exercices : Les triangles - 5e
Classe:
Cinquième
Exercice 1
$ABC$ est triangle, complétons le tableau.
Pour remplir ce tableau, il faut utiliser les propriétés suivantes :
$-\ $ La somme des mesures des angles d'un triangle est égale à $180^{\circ}$ donc,
$$mes\;\widehat{A}+mes\;\widehat{B}+mes\;\widehat{C}=180^{\circ}$$
Par conséquent,
$mes\;\widehat{A}=180^{\circ}-(mes\;\widehat{B}+mes\;\widehat{C})$
$mes\;\widehat{B}=180^{\circ}-(mes\;\widehat{A}+mes\;\widehat{C})$
$mes\;\widehat{C}=180^{\circ}-(mes\;\widehat{A}+mes\;\widehat{B})$
$-\ $ Un triangle qui possède un angle de $90^{\circ}$ est un triangle rectangle.
$-\ $ Si un triangle possède deux angles de même mesure, il est dit isolé.
$-\ $ Un triangle dont les mesures des angles sont différentes est un triangle quelconque.
$$\begin{array}{|c|c|c|c|c|c|}\hline mes\;\widehat{A}&30^{\circ}&63.5^{\circ}&45^{\circ}&138^{\circ}&20^{\circ}\\ \hline mes\;\widehat{B}&60^{\circ}&103^{\circ}&90^{\circ}&13^{\circ}&90^{\circ}\\ \hline mes\;\widehat{C}&90^{\circ}&13.5^{\circ}&45^{\circ}&29^{\circ}&70^{\circ} \\ \hline\text{Nature de }&\text{rectangle}&&\text{isocèle et}&&\text{rectangle}\\ABC&\text{en }C&\text{quelconque}&\text{rectangle}&\text{quelconque}&\text{en }B\\&&&\text{en }B&&\\ \hline\end{array}$$
Exercice 2
1) Construisons un triangle $ABC$ tel que :
$$AB=5\;cm\;;\ AC=4\;cm\quad\text{et}\quad BC=6\;cm$$
2) Traçons les droites $(d)\ $ et $\ (d')$ médiatrices respectifs des segments $[AB]\ $ et $\ [BC].$
On rappelle que la médiatrice d'un segment, c'est la droite passant par le milieu de ce segment et qui lui est perpendiculaire.
Soit alors, $I$ milieu de $[AB]\ $ et $J$ milieu de $[BC].$
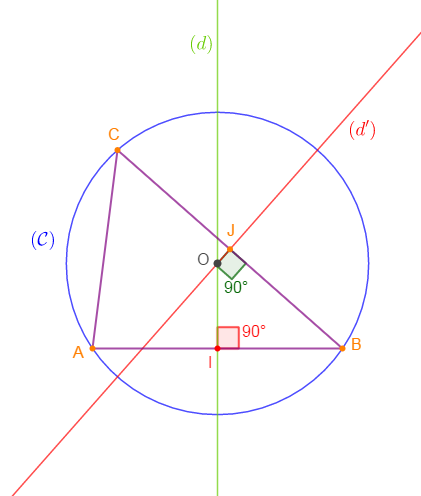
3) Construisons le cercle $(\mathcal{C})$ circonscrit à $ABC.$
On sait que dans un triangle les trois médiatrices sont concourantes en un même point appelé centre du cercle circonscrit à ce triangle.
Donc, soit $O$ le point de rencontre de $(d)\ $ et $\ (d')$ alors, $(\mathcal{C})$ est le cercle de centre $O$ passant par les sommets du triangle $ABC.$
Exercice 3
1) Construisons un triangle $MNP$ tel que :
$$MN=6\;cm\;;\ mes\;\widehat{M}=50^{\circ}\quad\text{et}\quad mes\;\widehat{N}=70^{\circ}$$
2) Calculons la mesure de l'angle $\widehat{P}.$
On sait que la somme des mesures des angles d'un triangle est toujours égale à $180^{\circ}.$
Donc,
$$mes\;\widehat{M}+mes\;\widehat{N}+mes\;\widehat{P}=180^{\circ}$$
Ainsi,
$\begin{array}{rcl} mes\;\widehat{P}&=&180^{\circ}-(mes\;\widehat{M}+mes\;\widehat{N})\\\\&=&180^{\circ}-(50^{\circ}+70^{\circ})\\\\&=&180^{\circ}-120^{\circ}\\\\&=&60^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{P}=60^{\circ}}$
3) Construisons les droites $(b)\ $ et $\ (b')$ bissectrices des angles $\widehat{M}\ $ et $\ \widehat{P}.$
On rappelle bissectrice d'un angle est la droite qui partage l'angle en deux angles de même mesure.
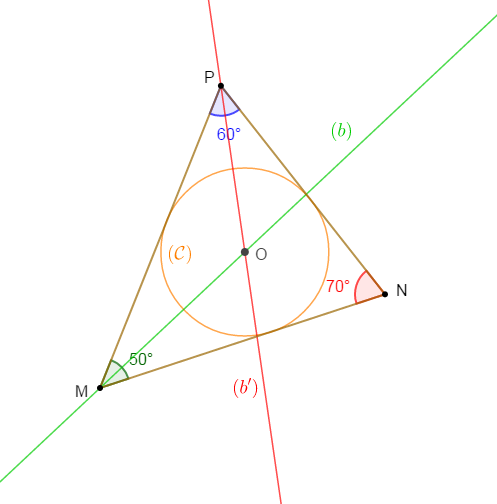
4) Construisons le cercle $(\mathcal{C})$ inscrit à $MNP.$
Dans un triangle, les trois bissectrices sont concourantes en un même point appelé centre du cercle inscrit dans ce triangle.
Soit alors $O$ le point de rencontre des droites $(b)\ $ et $\ (b').$
$O$ est donc le centre du cercle $(\mathcal{C})$ inscrit à $MNP.$


Exercice 10
1) a) Construisons un triangle $ABC$ tel que : $AB=AC=5\;cm\ $ et $\ mes\;\widehat{ABC}=70^{\circ}.$
b) $ABC$ est un triangle isocèle en $A.$
Justification :
En effet, on remarque que les deux côtés $[AB]\ $ et $\ [AC]$ ont la même longueur ; $5\;cm$ donc, le triangle $ABC$ est isocèle en $A.$
2) a) Construisons le point $D$ symétrique de $B$ par rapport à $A.$
b) $ADC$ est un triangle isocèle en $A.$
En effet, $D$ est symétrique de $B$ par rapport à $A$ donc, $A$ est milieu du segment $[BD].$
Par suite, $AD=AB=5\;cm$
Mais, on sait que $AB=AC=5\;cm$ donc, $AD=AC=5\;cm.$
D'où, $ADC$ isocèle en $A.$
3) Calculons : $mes\;\widehat{BAC}\;;\ mes\;\widehat{CAD}\ $ et $\ mes\;\widehat{ADC}.$
$-\ $ Calcul de $mes\;\widehat{BAC}$
On sait que la somme des mesures des angles d'un triangle est toujours égale à $180^{\circ}.$
Donc, pour le triangle $ABC$ on a :
$$mes\;\widehat{BAC}+mes\;\widehat{ACB}+mes\;\widehat{ABC}=180^{\circ}$$
Ainsi, $mes\;\widehat{BAC}=180^{\circ}-(mes\;\widehat{BCA}+mes\;\widehat{ABC})$
Comme, $ABC$ est isocèle en $A$ alors,
$$mes\;\widehat{BCA}=mes\;\widehat{ABC}=70^{\circ}$$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} mes\;\widehat{BAC}&=&180^{\circ}-(mes\;\widehat{BCA}+mes\;\widehat{ABC})\\\\&=&180^{\circ}-(70^{\circ}+70^{\circ})\\\\&=&180^{\circ}-140^{\circ}\\\\&=&40^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{BAC}=40^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{CAD}$
Les points $B\;,\ A\;,\ D$ sont alignés donc, les angles $\widehat{CAD}\ $ et $\ \widehat{BAC}$ sont supplémentaires.
Donc,
$$mes\;\widehat{CAD}+mes\;\widehat{BAC}=180^{\circ}$$
Par suite,
$\begin{array}{rcl} mes\;\widehat{CAD}&=&180^{\circ}-mes\;\widehat{BAC}\\\\&=&180^{\circ}-40^{\circ}\\\\&=&140^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{CAD}=140^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{ADC}$
On sait que la somme des mesures des angles d'un triangle est toujours égale à $180^{\circ}.$
Donc, pour le triangle $ADC$ on a :
$$mes\;\widehat{ADC}+mes\;\widehat{DCA}+mes\;\widehat{CAD}=180^{\circ}$$
Comme, $ADC$ est isocèle en $A$ alors,
$$mes\;\widehat{DCA}=mes\;\widehat{ADC}$$
Dans l'égalité précédente, on remplace $mes\;\widehat{DCA}$ par $mes\;\widehat{ADC}.$ On obtient alors :
$$mes\;\widehat{ADC}+mes\;\widehat{ADC}+mes\;\widehat{CAD}=180^{\circ}$$
Ce qui donne :
$$2\times mes\;\widehat{ADC}+mes\;\widehat{CAD}=180^{\circ}$$
Par suite,
$\begin{array}{rcl} 2\times mes\;\widehat{ADC}&=&180^{\circ}-mes\;\widehat{CAD}\\\\&=&180^{\circ}-140^{\circ}\\\\&=&40^{\circ}\end{array}$
Ainsi, $2\times mes\;\widehat{ADC}=40^{\circ}$
D'où, $\boxed{mes\;\widehat{ADC}=\dfrac{40^{\circ}}{2}=20^{\circ}}$
4) En déduisons $mes\;\widehat{BCD}$ et la nature de $BCD.$
On remarque que les angles $\widehat{BCA}\ $ et $\ \widehat{ACD}$ sont adjacents.
Donc,
$$mes\;\widehat{BCD}=mes\;\widehat{BCA}+mes\;\widehat{ACD}$$
Or, $ABC$ isocèle en $A$ donc, $mes\;\widehat{BCA}=mes\;\widehat{ABC}=70^{\circ}$
De même, $ADC$ isocèle en $A$ donc, $mes\;\widehat{ACD}=mes\;\widehat{ADC}=20^{\circ}$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} mes\;\widehat{BCD}&=&mes\;\widehat{BCA}+mes\;\widehat{ACD}\\\\&=&70^{\circ}+20^{\circ}\\\\&=&90^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{BCD}=90^{\circ}}$
La mesure de l'angle $\widehat{BCD}$ étant égale à $90^{\circ}$ donc, le triangle $BCD$ est rectangle en $C.$
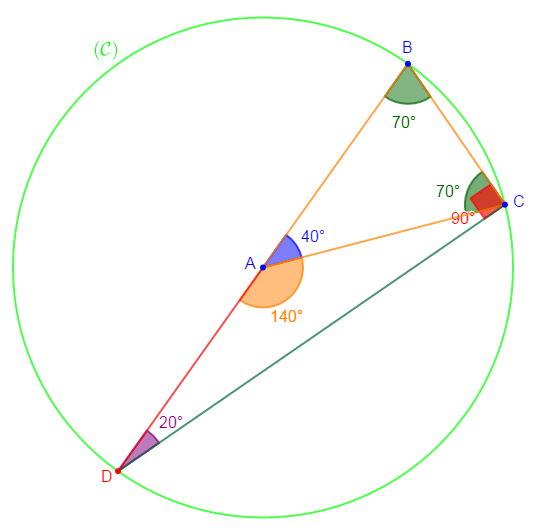
5) Construisons le cercle $(\mathcal{C})$ circonscrit à $BDC.$
Comme $BDC$ est un triangle rectangle en $C$ alors, le cercle $(\mathcal{C})$ circonscrit à $BDC$ a pour centre le milieu de l'hypoténuse qui est représenté par le côté $[BD].$
Or, $A$ est le milieu de $[BD]$ donc, le cercle $(\mathcal{C})$ circonscrit à $BDC$ a pour centre le point $A.$

Exercice 11
Parmi les affirmations données ci-dessous certaines sont vraies d'autres sont fausses.
Recopions celles qui sont fausses et corrigeons-les.
3) Les deux côtés de l'angle droit d'un triangle rectangle sont des hauteurs.
5) L'orthocentre d'un triangle rectangle est le sommet de l'angle droit de ce triangle.
6) Le centre du cercle circonscrit à un triangle rectangle se trouve au milieu de l'hypoténuse.
8) Un triangle rectangle dont l'un des angles mesure $45^{\circ}$ est rectangle et isocèle.
Exercice 13
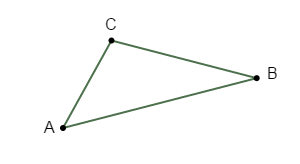
On considère les trois triangles ci-dessous.

1) Donnons la nature de chacun de ces triangles en justifiant.
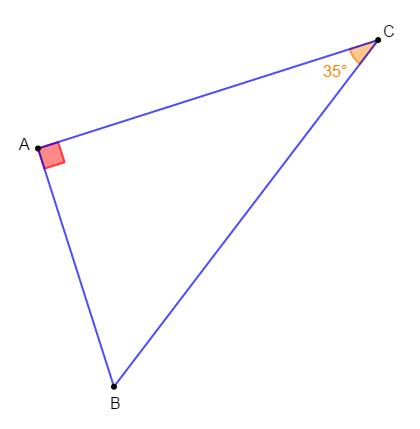
$-\ $ Le triangle $ABC$ est rectangle en $B.$
D'après le codage de la figure, on observe un angle droit en $B.$
Ainsi, $ABC$ est un triangle rectangle en $B.$
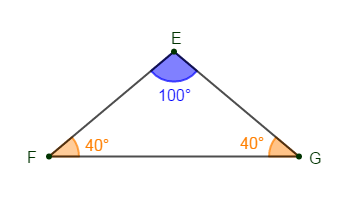
$-\ $ Le triangle $EFG$ est isocèle en $E.$
En observant le codage de la figure, on remarque que les côtés $[EF]\ $ et $\ [EG]$ ont même longueur.
Par conséquent, le triangle $EFG$ est isocèle en $E.$
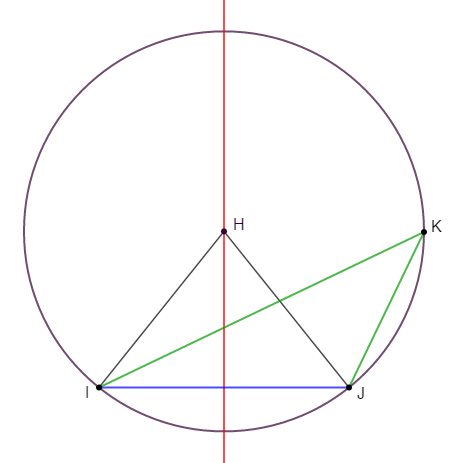
$-\ $ Le triangle $HIJ$ est équilatéral.
En observant le codage de la figure, on constate que les trois côtés $[HI]\;;\ [HJ]\ $ et $\ [IJ]$ sont de même longueur.
Par conséquent, $HIJ$ est un triangle équilatéral.
2) Donnons la mesure de chacun des angles $\alpha_{1}\;,\ \alpha_{2}\ $ et $\ \alpha_{3}$
Comme $ABC$ est un triangle rectangle en $B$ alors, $\alpha_{1}=90^{\circ}$
Comme $EFG$ est isocèle en $E$ alors, les angles à la base ont même mesure.
Ce qui signifie que : $\alpha_{2}=\widehat{EGF}$
Or, $\widehat{FGE}=68^{\circ}$ donc, $\alpha_{2}=68^{\circ}$
Comme $HIJ$ est un triangle équilatéral alors, ses trois angles internes ont la même mesure de $60^{\circ}.$
Par conséquent, $\alpha_{3}=60^{\circ}$
Exercice 14
1) Dans chacun des cas ci-dessous construisons le triangle indiqué en laissant les traits de construction :
a) $EDF$ tel que : $ED=6\;cm\;;\ \widehat{FED}=60^{\circ}\;;\ \widehat{FDE}=30^{\circ}.$
b) $CDE$ tel que : $CD=8\;cm\;;\ CE=5\;cm\ $ et $\ DE=4\;cm.$
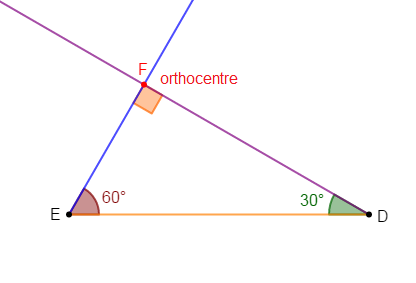
2) Plaçons l'orthocentre du triangle $EDF.$
L'orthocentre de ce triangle est le point $F.$
En effet, on a :
$\begin{array}{rcl}\widehat{FED}+\widehat{FDE}&=&60^{\circ}+30^{\circ}\\\\&=&90^{\circ}\end{array}$
Donc, $\widehat{FED}+\widehat{FDE}=90^{\circ}$
Ce qui signifie que les angles $\widehat{E}\ $ et $\ \widehat{D}$ sont complémentaires.
D'où, le triangle $EDF$ est rectangle en $F$
Par conséquent, $F$ est l'orthocentre du triangle $EDF.$

3) Construisons le cercle circonscrit au triangle $CDE.$
On trace alors les trois médiatrices du triangle $CDE.$
Le point de rencontre $O$ de ces trois médiatrices est le centre du cercle circonscrit au triangle $CDE.$

Exercice 15
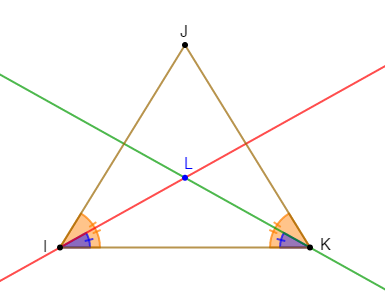
On considère un triangle $IJK$ isocèle en $J.$
Les bissectrices des angles $\widehat{I}\ $ et $\ \widehat{K}$ se coupent en un point $L.$
1) Montrons que $\widehat{LIK}=\widehat{IKL}.$
En effet, on a :
$(IL)$ est bissectrice de l'angle $\widehat{I}$ donc, $\widehat{JIK}=2\widehat{LIK}$
$(KL)$ est bissectrice de l'angle $\ \widehat{K}$ alors, $\widehat{IKJ}=2\widehat{IKL}$
Or, on sait que le triangle $IJK$ est isocèle en $J$ donc, les angles $\widehat{JIK}\ $ et $\ \widehat{IKJ}$ ont même mesure.
Ce qui signifie que : $\widehat{JIK}=\widehat{IKJ}$
Par conséquent, $2\widehat{LIK}=2\widehat{IKL}$
Ce qui donne : $\widehat{LIK}=\dfrac{2\widehat{IKL}}{2}=\widehat{IKL}$
D'où, $\boxed{\widehat{LIK}=\widehat{IKL}}$
2) Déduisons-en la nature du triangle $IKL.$
Le triangle $IKL$ est isocèle en $L.$
Justifions notre réponse.
D'après le résultat de la question $1)$, on a : $\widehat{LIK}=\widehat{IKL}$
Cela signifie que le triangle $IKL$ a deux angles de même mesure.
Or, on sait que : un triangle qui a deux angles de même mesure est un triangle isocèle.
Par conséquent, $IKL$ est isocèle en $L.$

Exercice 16
On considère le triangle $ABC$ ci-dessous.

1) Le triangle $ABC$ est rectangle en $A.$
Justifions notre réponse
D'après le codage de la figure, on a : $D$ milieu du segment $[CB].$
On a aussi : $DA=DB=DC.$
Ce qui signifie que le point $D$, milieu du côté $[CB]$, est à égale distance des trois sommets du triangle $ABC.$
Or, on sait que : si dans un triangle, le milieu d'un côté est à égale distance des trois sommets alors, ce triangle est rectangle.
Donc, $ABC$ est rectangle en $A.$
2) Le point $D$ est le centre du cercle circonscrit au triangle $ABC.$
Justifions notre réponse
En effet, comme $ABC$ est un triangle rectangle en $A$ alors, le côté $[CB]$ représente l'hypoténuse de milieu $D.$
Or, on sait que : le cercle circonscrit à un triangle rectangle a pour centre le milieu de l'hypoténuse.
Par conséquent, $D$ est le centre du cercle circonscrit au triangle $ABC.$
3) Calculons $\widehat{B}+\widehat{C}$
Comme $ABC$ est un triangle rectangle en $A$ alors, les angles $\widehat{B}\ $ et $\ \widehat{C}$ sont complémentaires.
Ce qui signifie que : $\boxed{\widehat{B}+\widehat{C}=90^{\circ}}$
Exercice 17
1) Construisons un cercle $(\gamma)$ de centre $O$ et de rayon $3\;cm$ puis marquons sur $(\gamma)$ deux points $A\ $ et $\ B$ diamétralement opposés.
2) La médiatrice de $[AB]$ coupe le cercle en $C\ $ et $\ D.$
Plaçons les points $C\ $ et $\ D$ puis précisons la nature exacte des triangles $ABC\ $ et $\ ABD.$
$ABC\ $ et $\ ABD$ sont des triangles rectangles respectivement en $C\ $ et $\ D.$
En effet, on sait que : si on joint un point d'un cercle aux extrémités d'un de ses diamètres ne contenant pas ce point alors, on obtient un triangle rectangle.
Or, $C$ est un point du cercle $(\gamma)$ et on a joint $C$ aux extrémités $A\ $ et $\ B$ du diamètre $[AB]$ de ce cercle.
Donc, $ABC$ est un triangle rectangle en $C.$
De la même manière, on constate qu'on a joint le point $D\in(\gamma)$ aux extrémités $A\ $ et $\ B$ du diamètre $[AB]$ du cercle $(\gamma).$
Par conséquent, $ABD$ est un triangle rectangle en $D.$
3) $M$ est un point de $(\gamma)$ tel que $\widehat{ABM}=35^{\circ}.$
Calculons les mesures des angles du triangle $MAB$ en justifiant.
Soit $M$ un point du cercle $(\gamma).$
Comme on a joint $M$ aux extrémités $A\ $ et $\ B$ du diamètre $[AB]$ de ce cercle alors, le triangle $ABM$ est rectangle en $M.$
Donc, l'angle $\widehat{AMB}$ est un angle droit.
Ce qui signifie que : $\boxed{\widehat{AMB}=90^{\circ}}$
On sait que dans un triangle rectangle les angles aigus sont complémentaires.
Or, $ABM$ rectangle en $M$ donc, $\widehat{ABM}\ $ et $\ \widehat{MAB}$ sont complémentaires.
Ce qui signifie : $\widehat{ABM}+\widehat{MAB}=90^{\circ}.$
Ce qui donne alors : $\widehat{MAB}=90^{\circ}-\widehat{ABM}$
En remplaçant $\widehat{ABM}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{MAB}&=&90^{\circ}-\widehat{ABM}\\\\&=&90^{\circ}-35^{\circ}\\\\&=&55^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{MAB}=55^{\circ}}$

Exercice 18
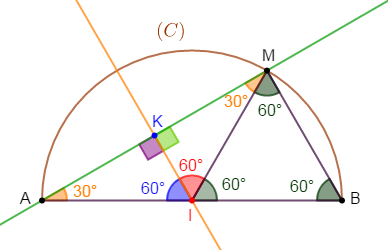
1) Traçons le demi-cercle $(C)$ de diamètre $[AB]$ tel que $AB=6\;cm.$
2) Plaçons le point $I$ milieu de $[AB]\ $ et $\ M$ un point de $(C)$ tel que $\widehat{MIB}=60^{\circ}.$
Précisons la nature du triangle $MIB$ et déduisons-en la mesure de ses angles.
$MIB$ est un triangle équilatéral.
Par conséquent, ses angles ont la même mesure de $60^{\circ}$
En effet, on a : $M$ appartient à $(C)$ alors, $MI=IB.$
Donc, le triangle $MIB$ est isocèle en $I$ tel que $\widehat{MIB}=60^{\circ}.$
Or, on sait que : si un triangle isocèle a un angle de $60^{\circ}$ alors, c'est un triangle équilatéral.
D'où, $MIB$ est un triangle équilatéral.
3) La parallèle à $(MB)$ passant par $I$ coupe $(AM)$ en $K.$
Calculons en justifiant les angles des triangles $MIK\ $ et $\ AKI.$
Soit $M$ un point du demi-cercle $(C).$
Comme on a joint $M$ aux extrémités $A\ $ et $\ B$ du diamètre $[AB]$ de ce demi-cercle alors, le triangle $ABM$ est rectangle en $M.$
Donc, l'angle $\widehat{AMB}$ est un angle droit.
Par suite, les angles $\widehat{AMB}\ $ et $\ \widehat{AMB}$ sont adjacents complémentaires.
Ce qui signifie : $\widehat{AMI}+\widehat{IMB}=\widehat{AMB}=90^{\circ}$
Ce qui donne alors : $\widehat{AMI}=90^{\circ}-\widehat{IMB}$
En remplaçant $\widehat{IMB}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{AMI}&=&90^{\circ}-\widehat{IMB}\\\\&=&90^{\circ}-60^{\circ}\\\\&=&30^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{AMI}=30^{\circ}}$
On a : $M$ appartient à $(C)$ alors, $MI=IA.$
Donc, le triangle $MIA$ est isocèle en $I.$
Par conséquent, $\widehat{IAM}=\widehat{AMI}$
Or, $\widehat{AMI}=30^{\circ}$ donc, $\boxed{\widehat{IAM}=30^{\circ}}$
On a : $(IK)$ parallèle à $(MB)\ $ et $\ (AM)$ perpendiculaire à $(MB).$
Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Donc, $(AM)$ est aussi perpendiculaire à $(IK).$
Par conséquent, les triangles $MIK\ $ et $\ AKI$ sont rectangles en $K.$
D'où, $\boxed{\widehat{MKI}=90^{\circ}\ \text{ et }\ \widehat{AKI}=90^{\circ}}$
Comme $AKI$ est rectangle en $K$ alors, les angles $\widehat{AIK}\ $ et $\ \widehat{KAI}$ sont complémentaires.
Ce qui signifie : $\widehat{AIK}+\widehat{IAK}=90^{\circ}.$
Ce qui donne alors : $\widehat{AIK}=90^{\circ}-\widehat{IAK}$
En remplaçant $\widehat{IAK}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{AIK}&=&90^{\circ}-\widehat{IAK}\\\\&=&90^{\circ}-30^{\circ}\\\\&=&60^{\circ}\end{array}$
Donc, $\boxed{\widehat{AIK}=60^{\circ}}$
De la même manière, comme $MIK$ est rectangle en $K$ alors, les angles $\widehat{MIK}\ $ et $\ \widehat{KMI}$ sont complémentaires.
Ce qui signifie : $\widehat{MIK}+\widehat{KMI}=90^{\circ}.$
Ce qui donne alors : $\widehat{MIK}=90^{\circ}-\widehat{KMI}$
En remplaçant $\widehat{KMI}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{MIK}&=&90^{\circ}-\widehat{KMI}\\\\&=&90^{\circ}-30^{\circ}\\\\&=&60^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{MIK}=60^{\circ}}$

Exercice 19
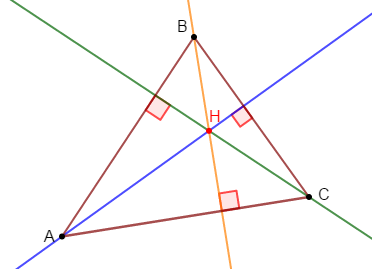
1) Construisons un triangle $ABC$ et plaçons son orthocentre $H.$
Pour cela, on trace les trois hauteurs du triangle $ABC$ et le point de rencontre de ces trois hauteurs est l'orthocentre $H.$
2) Les orthocentres des triangles $AHB\ $ et $\ AHC$ sont respectivement les points $C\ $ et $\ B.$
Dans le triangle $AHB$, on a :
$(HC)$ est la hauteur issue de $H$
$(AC)$ est la hauteur issue de $A$
$(BC)$ est la hauteur issue de $B$
On remarque alors que ces trois hauteurs se coupent au point $C.$
Par conséquent, $C$ est l'orthocentre du triangle $AHB.$
De la même manière, dans le le triangle $AHC$, on a :
$(HB)$ est la hauteur issue de $H$
$(AB)$ est la hauteur issue de $A$
$(BC)$ est la hauteur issue de $B$
On constate que ces trois hauteurs se coupent au point $B.$
Ce qui signifie que $B$ est l'orthocentre du triangle $AHB.$

Exercice 20
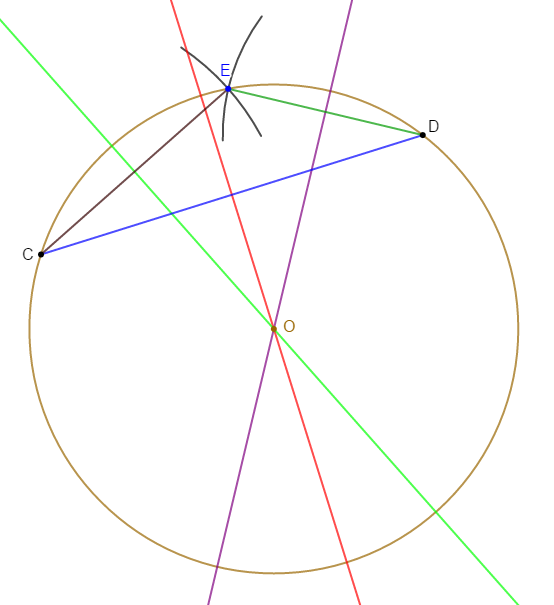
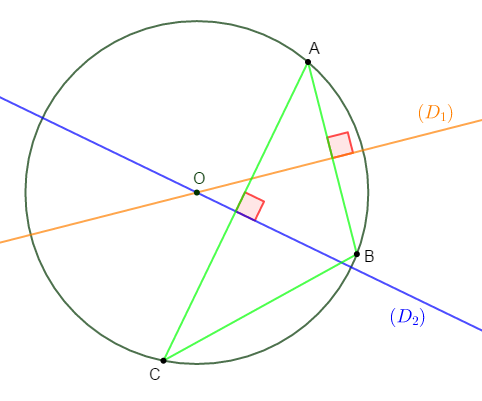
1) Traçons deux droites $(D_{1})\ $ et $\ (D_{2})$ sécantes en un point $O$ et plaçons un point $A$ n'appartenant pas à ces droites.
2) Construisons le point $B$ symétrique de $A$ par rapport à $(D_{1})$ et le point $C$ symétrique de $A$ par rapport à $(D_{2}).$
3) Le point $O$ est le centre du cercle circonscrit au triangle $ABC$
Justifions notre réponse.
On a : $B$ symétrique de $A$ par rapport à $(D_{1}).$ Cela signifie que $(D_{1})$ est la médiatrice du segment $[AB].$
On a aussi : $C$ symétrique de $A$ par rapport à $(D_{2}).$ Ce qui signifie que $(D_{2})$ est la médiatrice du segment $[AC].$
De plus, $(D_{1})\ $ et $\ (D_{2})$ sont sécantes en $O.$
On peut donc dire que les deux médiatrices $(D_{1})\ $ et $\ (D_{2})$ du triangle $ABC$ se coupent au point $O.$
Or, on sait que le point de rencontre des médiatrices d'un triangle est le centre du cercle circonscrit à ce triangle.
Par conséquent, $O$ est le centre du cercle circonscrit au triangle $ABC.$

Exercice 21
Reproduisons et complétons le tableau ci- dessous.
$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Angles}&&&&&&\\\text{d'un}&\text{Triangle 1}&\text{Triangle 2}&\text{Triangle 3}&\text{Triangle 4}&\text{Triangle 5}&\text{Triangle 6}\\\text{triangle}&&&&&&\\\hline \widehat{a}&36^{\circ}&54^{\circ}&60^{\circ}&72^{\circ}&90^{\circ}&45^{\circ}\\\hline\widehat{b}&108^{\circ}&36^{\circ}&60^{\circ}&72^{\circ}&63^{\circ}&45^{\circ} \\\hline\widehat{c}&36^{\circ}&90^{\circ}&60^{\circ}&36^{\circ}&27^{\circ}&90^{\circ} \\\hline\widehat{a}+\widehat{b}&144^{\circ}&90^{\circ}&120^{\circ}&144^{\circ}&153^{\circ}&90^{\circ}\\\hline\text{Nature}&\text{isocèle}&\text{rectangle}&&\text{isocèle}&\text{rectangle}&\text{rectangle}\\\text{du}&\text{en }B&\text{en }C&\text{équilatéral}&\text{en }C&\text{en }A&\text{isocèle}\\\text{triangle}&&&&&&\text{en }C\\\hline\end{array}$$
Exercice 22
1) Les angles aigus d'un triangle rectangle sont complémentaires.
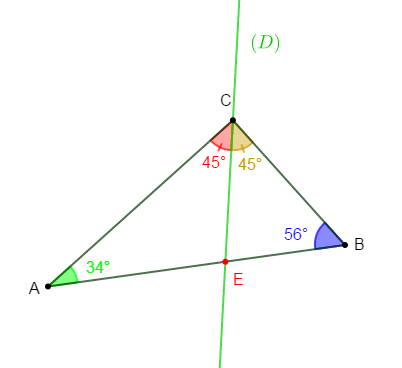
2) Construisons un triangle $ABC$ tel que $\widehat{ABC}=56^{\circ}\ $ et $\ \widehat{BAC}=34^{\circ}.$
3) Traçons $(D)$ la bissectrice de l'angle $\widehat{ACB}.\ (D)$ coupe $[AB]$ en $E.$
4) Calculons la mesure de chacun des angles $\widehat{ACE}\ $ et $\ \widehat{BCE}$
On constate d'abord que les angles $\widehat{ABC}\ $ et $\ \widehat{BAC}$ sont complémentaires.
En effet, on a : $\widehat{ABC}+\widehat{BAC}=56^{\circ}+34^{\circ}=90^{\circ}$ donc, $\widehat{ABC}\ $ et $\ \widehat{BAC}$ sont complémentaires.
Par conséquent, le triangle $ABC$ est rectangle en $C.$
D'où, $\widehat{ACB}=90^{\circ}$
Comme $(D)$ est la bissectrice de l'angle $\widehat{ACB}$ alors, la droite $(D)$ partage l'angle $\widehat{ACB}$ en deux angles de même mesure.
Ce qui signifie que : $\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}$
En remplaçant $\widehat{ACB}$ par sa valeur, on obtient : $\widehat{ACE}=\widehat{BCE}=\dfrac{90^{\circ}}{2}=45^{\circ}$
D'où, $\boxed{\widehat{ACE}=\widehat{BCE}=45^{\circ}}$

Exercice 23
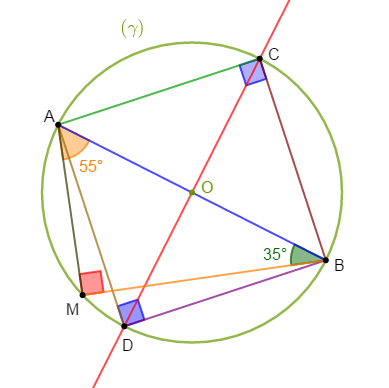
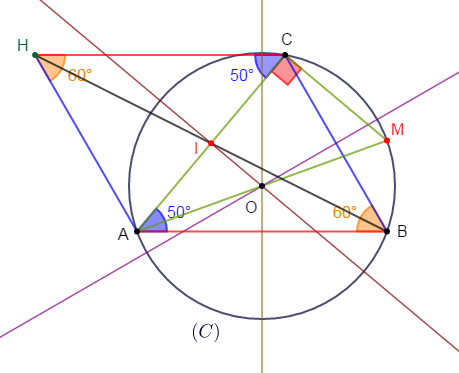
1) Traçons le triangle $ABC$ tel que :
$$AB=5\;cm\;,\ \widehat{CAB}=50^{\circ}\ \text{ et }\ \widehat{ABC}=60^{\circ}$$
Construisons le cercle $(C)$ de centre $O$ circonscrit au triangle $ABC.$
Pour cela, on trace les trois médiatrices du triangle $ABC.$
Le point de rencontre $O$ de ces trois médiatrices est alors le centre du cercle $(C)$ circonscrit à ce triangle.
2) Plaçons le point $M$ diamétralement opposé à $A.$
Le triangle $AMC$ est rectangle en $C.$
Justifions notre réponse.
En effet, on a : $M$ diamétralement opposé à $A$ donc, $[AM]$ est un diamètre du cercle $(C).$
De plus, on sait que : si on joint un point d'un cercle aux extrémités d'un de ses diamètres ne contenant pas ce point alors, on obtient un triangle rectangle.
Or, $C$ est un point du cercle $(C)$ et on a joint $C$ aux extrémités $A\ $ et $\ M$ du diamètre $[AM]$ de ce cercle.
Par conséquent, $AMC$ est un triangle rectangle en $C.$
3) a) Construisons le point $H$ symétrique de $B$ par rapport au point $I$ milieu de $[AC].$
b) Le quadrilatère $ABCH$ est un parallélogramme.
Justifions notre réponse.
On a : $H$ symétrique de $B$ par rapport au point $I$ alors, $I$ est milieu de $[BH].$
On a aussi : $I$ milieu de $[AC].$
Donc, on remarque que le quadrilatère $ABCH$ a ses diagonales de même milieu $I.$
Or, on sait que : si un quadrilatère a ses diagonales de milieu alors, c'est un parallélogramme.
D'où, $ABCH$ est un parallélogramme.
c) Déterminons la mesure de chacun des angles $\widehat{ACH}\ $ et $\ \widehat{AHC}.$
Comme $ABCH$ est un parallélogramme alors, $(HC)$ est parallèle à $(AB).$
Ainsi, $(HC)\ $ et $\ (AB)$ sont deux droites parallèles coupées par la sécante $(AC).$
Par conséquent, $\widehat{ACH}\ $ et $\ \widehat{CAB}$ sont deux angles alternes internes de même mesure.
Ce qui signifie alors : $\widehat{AHC}=\widehat{CAB}.$
Comme $\widehat{CAB}=50^{\circ}$ alors, $\boxed{\widehat{ACH}=50^{\circ}}$
Aussi, on sait que : dans un parallélogramme, deux angles opposés ont même mesure.
Or, dans le parallélogramme $ABCH$, les angles $\widehat{ACH}\ $ et $\ \widehat{ABC}$ sont opposés donc, ils ont la même mesure.
Ce qui signifie alors : $\widehat{ACH}=\widehat{ABC}$
Comme $\widehat{ABC}=60^{\circ}$ alors, $\boxed{\widehat{AHC}=60^{\circ}}$

Exercice 24
1) Construisons un triangle $ABC$ rectangle en $A$ tel que : $AB=5\;cm\ $ et $\ \widehat{ACB}=35^{\circ}.$

2) Construisons un triangle $EFG$ isocèle en $E$ avec $FG=5\;cm\ $ et $\ \widehat{FEG}=100^{\circ}.$

3) a) Traçons un segment $[IJ]$ de $5\;cm$ de longueur et plaçons $H$ un point n'appartenant pas à $[IJ]$ tel que $HI=HJ=4\;cm.$
Il faut remarquer que $H$ est sur la médiatrice du segment $[IJ].$
b) Construisons le triangle $IJK$ dont le cercle circonscrit a pour centre le point $H.$
Pour cela, on trace d'abord le cercle de centre $H$ et de rayon $4\,cm$
Ce cercle passe par les points $I\ $ et $\ J$ car $HI=HJ=4\;cm.$
Ensuite, on place le point $K$ sur ce même cercle.
On trace enfin le triangle $IJK.$
On constate alors que le cercle circonscrit à ce triangle a a pour centre le point $H.$

Exercice 25
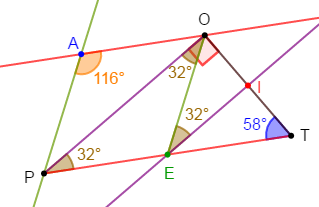
$POT$ est le triangle tel que :
$$PT=5\;cm\;,\ \widehat{OPT}=32^{\circ}\ \text{ et }\ \widehat{OTP}=58^{\circ}$$
1) $POT$ est un triangle rectangle en $O.$
Justifions notre réponse.
En effet, on a : $\widehat{OPT}+\widehat{OTP}=32^{\circ}+58^{\circ}=90^{\circ}$
On remarque alors que les angles aigus du triangle $POT$ sont complémentaires.
Par conséquent, le triangle $POT$ est rectangle en $O.$
Marquons le point $E$ milieu de $[PT].$
Le triangle $EOP$ est isocèle en $E.$
Justifions notre réponse.
En effet, le triangle rectangle $POT$ a pour hypoténuse le côté $[PT].$
Or, on sait que : dans un triangle rectangle, le milieu de l'hypoténuse est à égale distance des trois sommets du triangle.
Donc, le point $E$ est à égale distance des sommets $P\;;\ O\ $ et $\ T$ du triangle $POT.$
Cela signifie que les segments $[EP]\;;\ [EO]\ $ et $\ [ET]$ ont même longueur.
Ainsi, le triangle $EOP$ a deux côtés de même longueur.
Par conséquent, c'est un triangle isocèle en $E.$
2) La hauteur issue de $E$ dans le triangle $OET$ coupe le segment $[OT]$ en $I.$
a) Montrons que l'angle $\widehat{OEI}=32^{\circ}.$
On a : $(OP)$ perpendiculaire à $(OT)\ $ et $\ ((EI)$ perpendiculaire à $(OT).$
Or, on sait que : si deux droites sont perpendiculaires alors, toute droite perpendiculaire à l'une est parallèle à l'autre.
Donc, les droites $(OP)\ $ et $\ (EI)$ sont parallèles.
Alors, $(OP)\ $ et $\ (EI)$ sont deux droites parallèles coupées par la sécante $(OE).$
Par conséquent, $\widehat{OEI}\ $ et $\ \widehat{POE}$ sont deux angles alternes internes de même mesure.
Ce qui signifie alors : $\widehat{OEI}=\widehat{POE}.$
Or, $\widehat{POE}=\widehat{OPE}=32^{\circ}$ car le triangle $EOP$ est isocèle en $E.$
Ainsi, $\boxed{\widehat{OEI}=32^{\circ}}$
b) Justifions que la droite $(EI)$ est la bissectrice de l'angle $\widehat{OET}.$
On a : $EO=ET$ donc, le triangle $OET$ est isocèle en $E.$
Par conséquent, la hauteur $(EI)$ issue de $E$ est en même temps bissectrice de l'angle $\widehat{OET}.$
3) La parallèle à la droite $(OE)$ passant par $P$ et la parallèle à la droite $(PE)$ passant par $O$ se coupent en $A.$
a) Justifions que le quadrilatère $AOEP$ est un parallélogramme.
On a :
La parallèle à la droite $(OE)$ passe par $P\ $ et $\ A$ donc, les droites $(OE)\ $ et $\ (PA)$ sont parallèles.
La parallèle à la droite $(PE)$ passe par $O\ $ et $\ A$ donc, les droites $\ (PE)$ et $\ (OA)$ sont parallèles.
Ainsi, on constate que le quadrilatère $AOEP$ a ses côtés parallèles deux à deux.
Par conséquent, c'est un parallélogramme.
b) Justifions que l'angle $\widehat{PAO}= 116^{\circ}.$
On sait que : dans un parallélogramme, deux angles opposés ont même mesure.
Or, dans le parallélogramme $AOEP$, les angles $\widehat{PAO}\ $ et $\ \widehat{OEP}$ sont opposés donc, ils ont la même mesure.
Ce qui signifie alors : $\widehat{PAO}=\widehat{OEP}$
Cherchons alors la mesure de l'angle $\widehat{OEP}$
On sait que dans un triangle la somme des angles est égale à $180^{\circ}.$
Donc, $\widehat{OEP}+\widehat{OPE}+\widehat{POE}=180^{\circ}$
Ce qui entraine alors : $\widehat{OEP}=180^{\circ}-(\widehat{OPE}+\widehat{POE})$
En remplaçant $\widehat{OPE}\ $ et $\ \widehat{POE}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{OEP}&=&180^{\circ}-(\widehat{OPE}+\widehat{POE})\\\\&=&180^{\circ}-(32^{\circ}+32^{\circ})\\\\&=&180^{\circ}-64^{\circ}\\\\&=&116^{\circ}\end{array}$
Donc, $\widehat{OEP}=116^{\circ}$
Par conséquent, $\boxed{\widehat{PAO}=116^{\circ}}$

Exercice 27
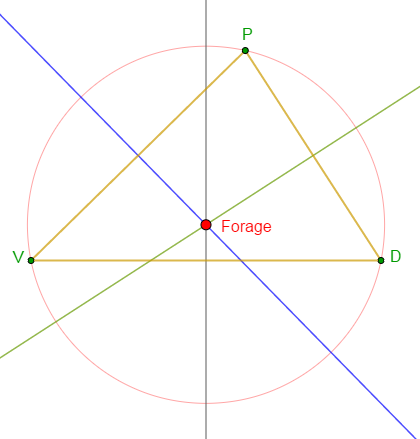
Pass, Véréane et Darou sont des villages du Sénégal situés sur des axes différents.
Ces villages sont désignés respectivement par les lettres $P\;,\ V\ $ et $\ D.$
Les distances entre ces villages sont les suivantes :
$$PV=600\;m\;,\ PD=500\;m\ \text{ et }\ VD=700 \;m$$
1) Représentons ces villages sur un plan à l'échelle $\dfrac{1}{10\,000}$
On donne d'abord les dimensions sur le plan.
On sait que si $D$ est la distance réelle et $e$ l'échelle alors, la distance $d$ sur le plan est donnée par :
$$d=D\times e$$
Donc, en appliquant cette propriété, on obtient :
$\begin{array}{rcl}PV&=&600\;m\times\dfrac{1}{10\,000}\\\\&=&\dfrac{600\;m}{10\,000}\\\\&=&0.06\,m\\\\&=&6\,cm\end{array}$
Donc, sur le plan $\boxed{PV=6\,cm}$
$\begin{array}{rcl}PD&=&500\;m\times\dfrac{1}{10\,000}\\\\&=&\dfrac{500\;m}{10\,000}\\\\&=&0.05\,m\\\\&=&5\,cm\end{array}$
Donc, sur le plan $\boxed{PD=5\,cm}$
$\begin{array}{rcl}VD&=&700\;m\times\dfrac{1}{10\,000}\\\\&=&\dfrac{700\;m}{10\,000}\\\\&=&0.07\,m\\\\&=&7\,cm\end{array}$
Donc, sur le plan $\boxed{VD=7\,cm}$
On trace ensuite le triangle $PVD$ tel que :
$$PV=6\;cm\;,\ PD=5\;cm\ \text{ et }\ VD=7\;cm$$

2) Une $O.N.G$ décide de leur construire un forage situé à égale distance des villages.
Nous sommes désignés pour choisir l'emplacement du forage.
Établissons sur le plan l'emplacement du forage en justifiant notre réponse.
En effet, on sait que le centre du cercle circonscrit à un triangle est à égale distance des sommets du triangle.
Donc, pour construire un forage situé à égale distance des villages, on choisira de le placer au centre du cercle circonscrit au triangle $PVD.$
Pour cela, on trace les trois médiatrices de ce triangle.
Le point de rencontre de ces trois médiatrices qui est le centre du cercle circonscrit désigne alors l'emplacement de ce forage.
Exercice 28
Notre école organise une kermesse durant laquelle un des jeux consiste à ramasser un mouchoir posé à terre.
Le premier à ramasser le mouchoir remporte le gain.
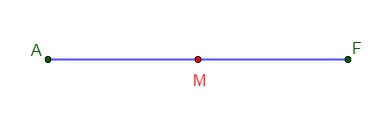
1) Deux filles Astou et Fama prennent position sur la même ligne.
On les désignera respectivement par les lettres $A\ $ et $\ F.$
Pour que le jeu soit équitable, on peut placer le mouchoir sur le milieu du segment $[AF].$
Donc, $M$ est milieu de $[AF]$
Faisons un schéma.

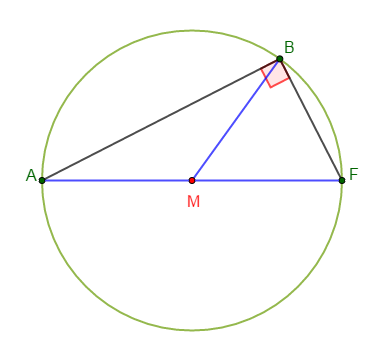
2) Bineta veut participer au jeu sans être sur la même ligne de départ que les $2$ autres filles.
Elle est désignée par la lettre $B.$
Plaçons $B$ sur le schéma précédent pour que le jeu soit équitable pour les $3$ candidates.
En effet, on sait que : dans un triangle rectangle, le milieu de l'hypoténuse est à égale distance des trois sommets du triangle.
On a : $M$ milieu du côté $[AF]$
Alors, pour que le mouchoir soit à égale distance des trois candidates, on va placer $B$ de sorte que le triangle $ABF$ soit rectangle en $B.$
3) Nous sommes chargés par nos camarades de donner toutes les positions possibles de tout concurrent afin que le jeu soit équitable.
Indiquons ces positions sur le schéma en justifiant notre réponse.
Afin que le jeu soit équitable, toutes les positions possibles de tout concurrent seront sur le cercle de diamètre $[AF].$
Donc, le cercle de diamètre $[AF]$ représente l'ensemble des positions possibles de tout concurrent afin que le jeu soit équitable.
En effet, on sait que le centre d'un cercle est à égale distance de tout point situé sur ce cercle.
Or, le centre d'un cercle est le milieu d'un de ses diamètres.
Donc, le milieu $M$ du segment $[AF]$ est le centre du cercle de diamètre $[AF].$
Par conséquent, $M$ est à égale distance de tout point situé sur le cercle de diamètre $[AF].$
Ainsi, pour que le jeu soit équitable, les concurrents seront positionnés sur le cercle de diamètre $[AF].$

Exercice 29
Pour financer ses activités, le foyer de notre école a aménagé un jardin ayant la forme d'un triangle $ABC$ dont les distances sont
$$AB=40\;m\;,\ AC=20\;m\ \text{ et }\ BC=30\;m$$
1) Représentons le jardin sur le plan à l'échelle $\dfrac{1}{1\,000}.$
On donne d'abord les dimensions sur le plan.
On sait que si $D$ est la distance réelle et $e$ l'échelle alors, la distance $d$ sur le plan est donnée par :
$$d=D\times e$$
Donc, en appliquant cette propriété, on obtient :
$\begin{array}{rcl}AB&=&40\;m\times\dfrac{1}{1\,000}\\\\&=&\dfrac{40\;m}{1\,000}\\\\&=&0.04\,m\\\\&=&4\,cm\end{array}$
Donc, sur le plan $\boxed{AB=4\,cm}$
$\begin{array}{rcl}AC&=&20\;m\times\dfrac{1}{1\,000}\\\\&=&\dfrac{20\;m}{1\,000}\\\\&=&0.02\,m\\\\&=&2\,cm\end{array}$
Donc, sur le plan $\boxed{AC=2\,cm}$
$\begin{array}{rcl}BC&=&30\;m\times\dfrac{1}{1\,000}\\\\&=&\dfrac{30\;m}{1\,000}\\\\&=&0.03\,m\\\\&=&3\,cm\end{array}$
Donc, sur le plan $\boxed{BC=3\,cm}$
On trace ensuite le triangle $PVD$ tel que :
$$AB=4\;cm\;,\ AC=2\;cm\ \text{ et }\ BC=3\;cm$$

2) Calculons le périmètre réel du jardin.
Pour cela, on utilise les distances réelles.
On a :
$\begin{array}{rcl}\text{Périmètre réel}&=&AB+AC+BC\\\\&=&40\;m+20\;m+30\;m\\\\&=&90\,m\end{array}$
Donc, le périmètre réel du jardin est égal à $90\,m$
3) On clôture le jardin avec du grillage vendu à $700\;F$ le mètre en laissant une porte de $4\;m$ de large et une autre de $3.5\;m$ de large.
Calculons le prix du grillage et le prix de revient de la clôture sachant qu'il faut $7$ piquets vendus à $500\;F$ pièce et qu'il faut payer $45\,000\;F$ pour la main d'œuvre.
$-\ $ Calcul du prix du grillage
Comme le grillage est vendu à $700\;F$ le mètre alors, on a :
$$\text{Prix du grillage}=700\times\text{longueur du grillage}$$
Comme on a laissé deux portes ; une $4\;m$ de large et une autre de $3.5\;m$ de large alors, la longueur du grillage nécessaire est donnée par :
$\begin{array}{rcl}\text{longueur du grillage}&=&\text{Périmètre réel}-(4\,m+3.5\,m)\\\\&=&90\,m-7.5\,m\\\\&=&82.5\,m\end{array}$
Donc, en remplaçant longueur du grillage par sa valeur, on obtient :
$\begin{array}{rcl}\text{Prix du grillage}&=&700\times\text{longueur du grillage}\\\\&=&700\times 82.5\\\\&=&57\,750\end{array}$
Ainsi, le prix du grillage est de $57\,750\;F$
$-\ $ Calcul du prix de revient de la clôture
On a :
$$\text{Prix de revient}=\text{Prix du grillage}+\text{Prix des piquets}+\text{Main d'œuvre}$$
Comme chaque piquet coûte $500\;F$ alors, le prix des $7$ piquets est donné par :
$\begin{array}{rcl}\text{Prix des piquets}&=&500\times 7\\\\&=&3\,500\end{array}$
Donc, le prix des $7$ piquets est de $3\,500\;F$
On obtient alors :
$\begin{array}{rcl}\text{Prix de revient}&=&\text{Prix du grillage}+\text{Prix des piquets}+\text{Main d'œuvre}\\\\&=&57\,750+3\,500+45\,000\\\\&=&106\,250\end{array}$
D'où, le prix de revient de la clôture est de $106\,250\;F$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
dim, 03/06/2022 - 19:40
Permalien
Comment vous aviez tracé la
Anonyme (non vérifié)
dim, 04/17/2022 - 20:07
Permalien
Soit ABC un triangle tel que
Anonyme (non vérifié)
dim, 04/17/2022 - 20:07
Permalien
Soit ABC un triangle tel que
Binta lô (non vérifié)
sam, 11/08/2025 - 22:12
Permalien
Pourquoi sunudara n'a pas l
Ajouter un commentaire