Solution des exercices : Angle au centre - angle inscrit 3e
Classe:
Troisième
Exercice 1
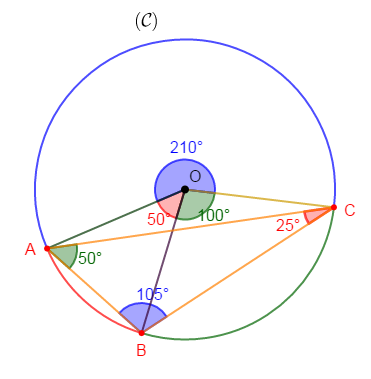
$ABC$ est un triangle inscrit dans un cercle $(C)$ de centre $O$ et tel que les angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ sont adjacents.
On donne : $mes\;\widehat{AOB}=50^{\circ}\;;\ mes\;\widehat{BOC}=100^{\circ}$
Calculons la mesure de chacun des angles du triangle $ABC.$
$-\ $ Calcul de $mes\;\widehat{ACB}$
En effet, $\widehat{ACB}$ est un angle inscrit dans $(C)$ ayant pour angle au centre associé $\widehat{AOB}.$
Alors on a :
$$mes\;\widehat{ACB}=\dfrac{mes\;\widehat{AOB}}{2}$$
Or, $mes\;\widehat{AOB}=50^{\circ}$
Donc, $mes\;\widehat{ACB}=\dfrac{50^{\circ}}{2}=25^{\circ}$
D'où, $\boxed{mes\;\widehat{ACB}=25^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{BAC}$
On a : $\widehat{BAC}$ est un angle inscrit dans $(C)$ ayant pour angle au centre associé $\widehat{BOC}.$
Donc,
$$mes\;\widehat{BAC}=\dfrac{mes\;\widehat{BOC}}{2}$$
Comme $mes\;\widehat{BOC}=100^{\circ}$ alors, $mes\;\widehat{BAC}=\dfrac{100^{\circ}}{2}=50^{\circ}$
Ainsi, $\boxed{mes\;\widehat{BAC}=50^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{ABC}$
On sait que la somme des angles d'un triangle est égale à $180^{\circ}$
Donc, dans le triangle $ABC$ on a :
$$mes\;\widehat{BAC}+mes\;\widehat{ABC}+mes\;\widehat{ACB}=180^{\circ}$$
Ainsi, $mes\;\widehat{ABC}=180^{\circ}-mes\;\widehat{BAC}-mes\;\widehat{ACB}$
Alors, en remplaçant $mes\;\widehat{BAC}\ $ et $\ mes\;\widehat{ACB}$ par leur valeur, on trouve :
$$mes\;\widehat{ABC}=180^{\circ}-50^{\circ}-25^{\circ}=105^{\circ}$$
D'où, $\boxed{mes\;\widehat{ABC}=105^{\circ}}$
On peut également remarquer que $\widehat{ABC}$ est un angle inscrit dans $(C)$ ayant pour angle au centre associé $A\check{O}C.$
Alors, $mes\;\widehat{ABC}=\dfrac{mes\;A\check{O}C}{2}$
Or,
$\begin{array}{rcl} mes\;A\check{O}C&=&360^{\circ}-(\widehat{AOB}+\widehat{BOC})\\\\&=&360^{\circ}-(50^{\circ}+100^{\circ})\\\\&=&360^{\circ}-150^{\circ}\\\\&=&210^{\circ}\end{array}$
Donc, $\boxed{mes\;A\check{O}C=210^{\circ}}$
Par suite, $mes\;\widehat{ABC}=\dfrac{210^{\circ}}{2}=105^{\circ}$
D'où, $\boxed{mes\;\widehat{ABC}=105^{\circ}}$
Exercice 2
$ABC$ est un triangle isocèle en $A\;,\ \mathcal{C}(O\;;\ R)$ son cercle circonscrit et $D$ un point diamétralement opposé à $B.$
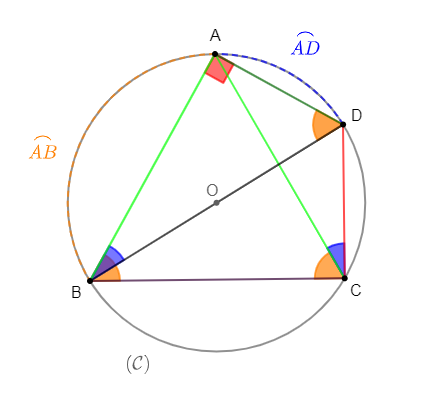
1) Démontrons que $\widehat{ADB}=\widehat{ABC}$
En effet, comme $ABC$ est isocèle en $A$ alors, les angles $\widehat{ACB}\ $ et $\ \widehat{ABC}$ ont la même mesure.
Donc,
$$mes\;\widehat{ACB}=mes\;\widehat{ABC}\qquad(\text{égalité 1})$$
Par ailleurs, $\widehat{ACB}\ $ et $\ \widehat{ADB}$ sont deux angles inscrits dans le cercle $(\mathcal{C})$ et interceptant le même arc de cercle $\overset{\displaystyle\frown}{AB}.$
Par conséquent, ils ont la même mesure.
Donc,
$$mes\;\widehat{ACB}=mes\;\widehat{ADB}\qquad(\text{égalité 2})$$
Ainsi, en comparant ces deux égalités, on a : $\boxed{mes\;\widehat{ADB}=mes\;\widehat{ABC}}$
2) Démontrons que $\widehat{DCA}\ $ et $\ \widehat{ADB}$ sont complémentaires.
Comme $[BD]$ est un diamètre alors, $ABD$ est un triangle rectangle en $A$
Or, les angles aigus d'un triangle rectangle sont complémentaires.
Donc,
$$mes\;\widehat{ADB}+mes\;\widehat{ABD}=90^{\circ}\qquad(\text{égalité 3})$$
Par ailleurs, $\widehat{ABD}\ $ et $\ \widehat{DCA}$ sont deux angles inscrits dans $(\mathcal{C})$ interceptant le même arc de cercle $\overset{\displaystyle\frown}{AD}.$
Alors, ils ont la même mesure.
Ce qui signifie : $mes\;\widehat{ABD}=mes\;\widehat{DCA}$
Ainsi, dans l'égalité $3$, en remplaçant $mes\;\widehat{ABD}$ par $mes\;\widehat{DCA}$, on trouve :
$$mes\;\widehat{ADB}+mes\;\widehat{DCA}=90^{\circ}$$
Ce qui montre que les angles $\widehat{DCA}\ $ et $\ \widehat{ADB}$ sont complémentaires.
Exercice 3
Traçons un cercle et un triangle $ABC$ dont les sommets appartiennent à ce cercle.
La bissectrice de l'angle $\widehat{BAC}$ coupe l'arc $\overset{\displaystyle\frown}{BC}$ en un point $I.$
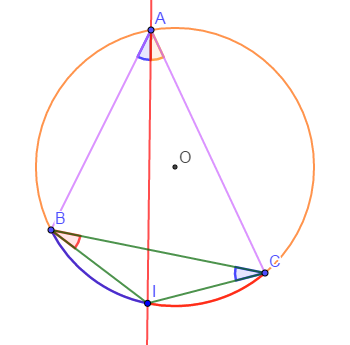
Démontrons que triangle $BIC$ est isocèle en $I.$
$\widehat{IAC}\ $ et $\ \widehat{IBC}$ étant deux angles inscrits dans le cercle et interceptant le même arc $\overset{\displaystyle\frown}{IC}$ alors, ils ont la même mesure.
Donc,
$$mes\;\widehat{IAC}=mes\;\widehat{IBC}$$
Or, la droite $(AI)$ est bissectrice de l'angle $\widehat{BAC}.$
Ce qui entraine : $mes\;\widehat{IAC}=mes\;\widehat{IAB}$
Par suite,
$$mes\;\widehat{IBC}=mes\;\widehat{IAB}$$
De la même manière, $\widehat{ICB}\ $ et $\ \widehat{IAB}$ sont deux angles inscrits dans le cercle et interceptant le même arc $\overset{\displaystyle\frown}{IB}$ donc, ils ont la même mesure.
Ce qui peut alors s'écrire :
$$mes\;\widehat{ICB}=mes\;\widehat{IAB}$$
Ainsi, on a : $mes\;\widehat{IBC}=mes\;\widehat{IAB}\ $ et $\ mes\;\widehat{ICB}=mes\;\widehat{IAB}$
Par conséquent,
$$mes\;\widehat{IBC}=mes\;\widehat{ICB}$$
D'où, le triangle $BIC$ est isocèle en $I.$
Exercice 4
Soit la figure ci-dessous :
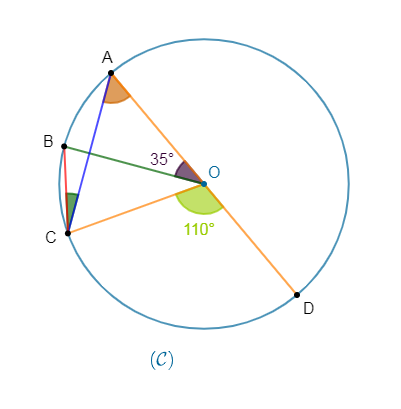
1) L'angle inscrit qui intercepte le même arc de cercle que $\widehat{AOB}$ est l'angle $\widehat{ACB}.$
2) Calculons la mesure de $\widehat{ACB}$
D'après le résultat de la question $1)$, on a : $\widehat{ACB}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{AOB}.$
Alors, on a :
$$mes\;\widehat{ACB}=\dfrac{mes\;\widehat{AOB}}{2}$$
Or, $mes\;\widehat{AOB}=35^{\circ}$
Donc, $mes\;\widehat{ACB}=\dfrac{35^{\circ}}{2}=17.5^{\circ}$
D'où, $\boxed{mes\;\widehat{ACB}=17.5^{\circ}}$
Calculons la mesure de $\widehat{DAC}.$
En effet, $\widehat{DAC}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{DOC}.$
Donc,
$$mes\;\widehat{DAC}=\dfrac{mes\;\widehat{COD}}{2}$$
Comme $mes\;\widehat{COD}=110^{\circ}$ alors, $mes\;\widehat{DAC}=\dfrac{110^{\circ}}{2}=55^{\circ}$
Ainsi, $\boxed{mes\;\widehat{DAC}=55^{\circ}}$
En déduisons la mesure de $\widehat{AOC}$
$AOC$ étant un triangle isocèle en $O$ alors, $mes\;\widehat{OAC}=mes\;\widehat{ACO}$
Or, $mes\;\widehat{OAC}=mes\;\widehat{DAC}=55^{\circ}$
Donc,
$$mes\;\widehat{OAC}=mes\;\widehat{ACO}=55^{\circ}$$
Par ailleurs, on sait que la somme des angles d'un triangle est égale à $180^{\circ}.$
Donc, dans le triangle $AOC$, on a :
$$mes\;\widehat{OAC}+mes\;\widehat{ACO}+mes\;\widehat{AOC}=180^{\circ}$$
Par suite,
$\begin{array}{rcl} \widehat{AOC}&=&180^{\circ}-\widehat{OAC}-\widehat{ACO}\\\\&=&180^{\circ}-55^{\circ}-55^{\circ}\\\\&=&180^{\circ}-110^{\circ}\\\\&=&70^{\circ}\end{array}$
D'où, $mes\;\widehat{AOC}=70^{\circ}$
On peut aussi constater que les angles $\widehat{AOC}\ $ et $\ \widehat{COD}$ sont adjacents supplémentaires.
Donc,
$$mes\;\widehat{AOC}+mes\;\widehat{COD}=180^{\circ}$$
Par suite, $mes\;\widehat{AOC}=180^{\circ}-mes\;\widehat{COD}$
En remplaçant $mes\;\widehat{COD}$ par sa valeur, on trouve :
$$mes\;\widehat{AOC}=180^{\circ}-110^{\circ}=70^{\circ}$$
D'où, $mes\;\widehat{AOC}=70^{\circ}$
Exercice 5
Soit sur la figure ci-dessous deux cercles $(C)$ et $(C')$ de centres respectifs $O$ et $O'.$

Démontrons que les angles $\widehat{MBN}$ et $\widehat{M'BN'}$ ont même mesure.
On a : $\widehat{MBN}=\widehat{MBN'}+\widehat{N'BN}\ $ et $\ \widehat{M'BN'}=\widehat{M'BM}+\widehat{MBN'}$
Donc, $\widehat{MBN}\ $ et $\ \widehat{M'BN'}$ ont même mesure si, et seulement si, $$\widehat{N'BN}=\widehat{M'BM}$$
Ainsi, il suffit de montrer que $\widehat{N'BN}=\widehat{M'BM}$ pour répondre à la question.
En considérant le cercle $(C')$ on constate que $\widehat{M'AM}$ et $\widehat{M'BM}$ sont deux angles inscrits interceptant le même arc de cercle $\overset{\displaystyle\frown}{MM'}$ donc sont égaux.
De même, en considérant le cercle $(C)$ on remarque que $\widehat{N'AN}$ et $\widehat{N'BN}$ sont deux angles inscrits interceptant le même arc de cercle $\overset{\displaystyle\frown}{NN'}$ donc sont égaux.
Alors on a :
$\left\lbrace\begin{array}{rcl} \widehat{M'AM}&=&\widehat{M'BM}\\ \\ \widehat{N'AN}&=&\widehat{N'BN}\end{array}\right.\quad\text{et}\quad\widehat{N'AN}=\widehat{M'AM}$
Donc, $\widehat{N'BN}=\widehat{M'BM}$
D'où, $\boxed{mes\;\widehat{MBN}=mes\;\widehat{M'BN'}}$
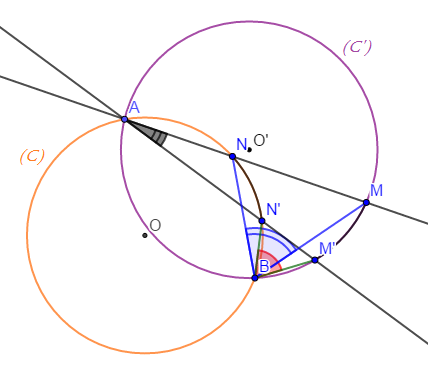
Exercice 6
1) Soit un cercle $(\mathcal{C})$ de centre $O$ et de rayon $4\;cm\ $ et $\ [AD]$ un de ses diamètres.
a) D'un côté de la droite $(AD)$, construisons le point $G$ tel que le triangle $ADG$ soit un triangle équilatéral.
b) De l'autre côté de la droite $(AD)$, plaçons le point $B$ du cercle $(\mathcal{C})$, tel que $AB=4\;cm.$

2) Démontrons que le triangle $OAB$ est équilatéral.
En effet, comme $A\ $ et $\ B$ appartiennent au cercle $(\mathcal{C})$ alors, les longueurs $OA\ $ et $\ OB$ sont égales au rayon de $(\mathcal{C}).$
Ce qui signifie que : $OA=OB=4\;cm$
Or, on sait que : $AB=4\;cm$
Donc,
$$OA=OB=AB=4\,cm$$
Ainsi, le triangle $OAB$ a ses côtés de même longueur par conséquent, c'est un triangle équilatéral.
3) Justifions que les angles $\widehat{OAB}\ $ et $\ \widehat{ADG}$ sont égaux puis, en déduisons la position relative des droites $(AB)\ $ et $\ (DG).$
En effet, d'après le résultat de la question $1)$, on a : $ADG$ est un triangle équilatéral.
Cela signifie que ses angles ont la même mesure de $60^{\circ}.$
Donc, $mes\;\widehat{ADG}=60^{\circ}$
De la même manière, d'après le résultat de la question $2)$, le triangle $OAB$ est équilatéral.
Par conséquent, ses angles ont la même mesure de $60^{\circ}.$
Donc, $mes\;\widehat{OAB}=60^{\circ}$
On constate alors que $\widehat{OAB}\ $ et $\ \widehat{ADG}$ sont de même mesure.
D'où, les angles $\widehat{OAB}\ $ et $\ \widehat{ADG}$ sont égaux.
En déduisons la position relative des droites $(AB)\ $ et $\ (DG).$
En effet, les droites $(AB)\ $ et $\ (DG)$ et la sécante $(AD)$ déterminent deux angles alternes internes $\widehat{OAB}\ $ et $\ \widehat{ADG}.$
Comme ces deux angles sont de même mesure alors, les droites $(AB)\ $ et $\ (DG)$ sont parallèles.
4) La droite $(BG)$ coupe $[AD]$ en $I\ $ et $\ (\mathcal{C})$ en $J.$
a) En utilisant le théorème de Thalès justifions que : $$\dfrac{IA}{ID}=\dfrac{1}{2}$$
En effet, les droites $(AD)\ $ et $\ (BG)$ sécantes en $I$ sont coupées par deux droites $(AB)\ $ et $\ (DG).$
Or, d'après le résultat de la question $3)$, on a : $(AB)\ $ et $\ (DG)$ sont parallèles.
Donc, les triangles $AIB\ $ et $\ DIG$ sont en position de Thalès.
Ainsi, en utilisant le théorème de Thalès, on a :
$$\dfrac{IA}{ID}=\dfrac{AB}{DG}$$
Or, on sait que $ADG$ est un triangle équilatéral.
Par conséquent : $DG=AD$
Comme $[AD]$ est un diamètre de $(\mathcal{C})$ alors, la longueur $AD$ est égale au double du rayon de $(\mathcal{C}).$
Donc, $AD=2\times 4=8\;cm$
Par suite, $DG=8\;cm$
Ainsi, dans l'égalité $\dfrac{IA}{ID}=\dfrac{AB}{DG}$, en remplaçant $AB\ $ et $\ DG$ par leur valeur, on obtient :
$\begin{array}{rcl}\dfrac{IA}{ID}&=&\dfrac{AB}{DG}\\\\&=&\dfrac{4}{8}\\\\&=&\dfrac{4\div 4}{8\div 4}\\\\&=&\dfrac{1}{2}\end{array}$
D'où, $\boxed{\dfrac{IA}{ID}=\dfrac{1}{2}}$
b) Calculons la mesure de l'angle $\widehat{AJB}$
En effet, $\widehat{AJB}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{AOB}.$
Donc,
$$mes\;\widehat{AJB}=\dfrac{mes\;\widehat{AOB}}{2}$$
Or, d'après le résultat de la question $2)$, le triangle $OAB$ est équilatéral.
Cela signifie que ses angles ont la même mesure de $60^{\circ}.$
Donc, $mes\;\widehat{AOB}=60^{\circ}$
Ainsi, $mes\;\widehat{AJB}=\dfrac{60^{\circ}}{2}=30^{\circ}$
D'où, $\boxed{mes\;\widehat{AJB}=30^{\circ}}$
Exercice 7
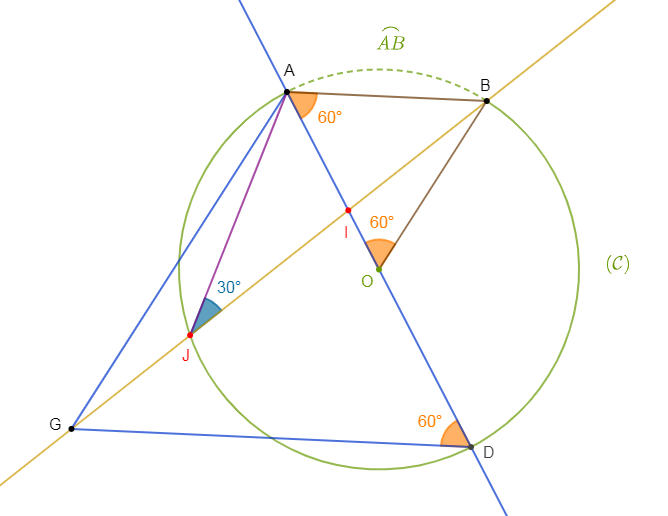
Plaçons trois points $A\;,\ B\ $ et $\ C$ dans cet ordre sur un cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm$, de telle façon que les angles au centre $\widehat{AOB}\ $ et $\ \widehat{BOC}$ mesurent respectivement $40^{\circ}\ $ et $\ 70^{\circ}.$
1) Calculons la mesure de tous les angles du triangle $ABC.$
En effet, en observant la figure, nous constatons que :
$\widehat{ACB}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{AOB}.$
Donc,
$$mes\;\widehat{ACB}=\dfrac{mes\;\widehat{AOB}}{2}$$
Or, $mes\;\widehat{AOB}=40^{\circ}$
Ainsi, $mes\;\widehat{ACB}=\dfrac{40^{\circ}}{2}=20^{\circ}$
D'où, $\boxed{mes\;\widehat{ACB}=20^{\circ}}$
$\widehat{CAB}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{BOC}.$
Donc,
$$mes\;\widehat{CAB}=\dfrac{mes\;\widehat{BOC}}{2}$$
Comme $mes\;\widehat{BOC}=70^{\circ}$ alors, $mes\;\widehat{CAB}=\dfrac{70^{\circ}}{2}=35^{\circ}$
D'où, $\boxed{mes\;\widehat{CAB}=35^{\circ}}$
Par ailleurs, on sait que la somme des angles d'un triangle est égale à $180^{\circ}.$
Donc,
$$\widehat{ABC}+\widehat{ACB}+\widehat{CAB}=180^{\circ}$$
Par suite,
$\begin{array}{rcl} \widehat{ABC}&=&180^{\circ}-\widehat{ACB}-\widehat{CAB}\\\\&=&180^{\circ}-20^{\circ}-35^{\circ}\\\\&=&125^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{ABC}=125^{\circ}}$
2) Calculons la longueur des arcs $\overset{\displaystyle\frown}{AB}\ $ et $\ \overset{\displaystyle\frown}{AC}.$ (on donne $\pi\cong 3).$
Soit : $\ell_{\overset{\displaystyle\frown}{AB}}$ la longueurs de l'arc de cercle intercepté par l'angle $\widehat{AOB}.$
Alors, on a :
$$\ell_{\overset{\displaystyle\frown}{AB}}=\pi\times\text{rayon de }(\mathcal{C})\times\dfrac{mes\;\widehat{AOB}}{180^{\circ}}$$
En remplaçant $\pi$, rayon de $(\mathcal{C})\ $ et $\ mes\;\widehat{AOB}$ par leur valeur, on trouve :
$\begin{array}{rcl} \ell_{\overset{\displaystyle\frown}{AB}}&=&\pi\times\text{rayon de }(\mathcal{C})\times\dfrac{mes\;\widehat{AOB}}{180^{\circ}}\\\\&=&3\times 3\times\dfrac{40}{180}\\\\&=&\dfrac{360}{180}\\\\&=&2\end{array}$
D'où, $\boxed{\ell_{\overset{\displaystyle\frown}{AB}}=2\;cm}$
Soit : $\ell_{\overset{\displaystyle\frown}{AC}}$ la longueurs de l'arc de cercle intercepté par l'angle $\widehat{AOC}.$
On a alors :
$$\ell_{\overset{\displaystyle\frown}{AC}}=\pi\times\text{rayon de }(\mathcal{C})\times\dfrac{mes\;\widehat{AOC}}{180^{\circ}}$$
Or, on sait que :
$\begin{array}{rcl} mes\;\widehat{AOC}&=&mes\;\widehat{AOB}+mes\;\widehat{BOC}\\\\&=&40^{\circ}+70^{\circ}\\\\&=&110^{\circ}\end{array}$
Donc, $\boxed{mes\;\widehat{AOC}=110^{\circ}}$
Ainsi, en remplaçant $\pi$, rayon de $(\mathcal{C})\ $ et $\ mes\;\widehat{AOC}$ par leur valeur, on trouve :
$\begin{array}{rcl} \ell_{\overset{\displaystyle\frown}{AC}}&=&\pi\times\text{rayon de }(\mathcal{C})\times\dfrac{mes\;\widehat{AOC}}{180^{\circ}}\\\\&=&3\times 3\times\dfrac{110}{180}\\\\&=&\dfrac{990}{180}\\\\&=&5.5\end{array}$
D'où, $\boxed{\ell_{\overset{\displaystyle\frown}{AC}}=5.5\;cm}$
3) Soit $M$ un point diamétralement opposés à $B.$ Calculons : $mes\;\widehat{BMC}\;;\ mes\;\widehat{AMC}\ $ et $\ mes\;\widehat{AMB}.$
$-\ $ Calcul de $mes\;\widehat{BMC}$
Dans le cercle $(\mathcal{C})$, nous constatons que $\widehat{BMC}\ $ et $\ \widehat{CAB}$ sont deux angles inscrits interceptant le même arc de cercle $\overset{\displaystyle\frown}{BC}.$
Donc, ces deux angles sont égaux.
Par suite, $mes\;\widehat{BMC}=mes\;\widehat{CAB}$
Or, d'après le résultat de la question $1)\;,\ mes\;\widehat{CAB}=35^{\circ}$
Par conséquent, $\boxed{mes\;\widehat{BMC}=35^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{AMC}$
En observant la figure, nous constatons que $\widehat{AMC}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{AOC}.$
Alors,
$$mes\;\widehat{AMC}=\dfrac{mes\;\widehat{AOC}}{2}$$
Or, $mes\;\widehat{AOC}=110^{\circ}$
Donc, $mes\;\widehat{AMC}=\dfrac{110^{\circ}}{2}=55^{\circ}$
D'où, $\boxed{mes\;\widehat{AMC}=55^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{AMB}$
Dans le cercle $(\mathcal{C})$, nous remarquons que $\widehat{AMB}\ $ et $\ \widehat{ACB}$ sont deux angles inscrits interceptant le même arc de cercle $\overset{\displaystyle\frown}{AB}.$
Donc, ces deux angles sont égaux.
Ainsi, $mes\;\widehat{AMB}=mes\;\widehat{ACB}$
Or, d'après le résultat de la question $1)\;,\ mes\;\widehat{ACB}=20^{\circ}$
D'où, $\boxed{mes\;\widehat{AMB}=20^{\circ}}$

Exercice 8 BFEM 2e groupe
Répondons par vrai ou faux en justifiant la réponse.
1) Si $a\ $ et $\ b$ sont deux angles inscrits qui interceptent le même arc de cercle alors, $mes\;a= 2\,mes\;b\quad(\text{Faux})$
En effet, on sait que dans un cercle, deux angles inscrits qui interceptent le même arc de cercle ont la même mesure.
D'où, $mes\;a=mes\;b$
2) Si $x\ $ et $\ y$ représentent deux angles inscrits qui interceptent le même arc de cercle alors, la mesure de $x$ est égale à la moitié de celle de $y.\quad(\text{Faux})$
Comme deux angles inscrits qui interceptent le même arc de cercle ont la même mesure alors, $mes\;x=mes\;y$
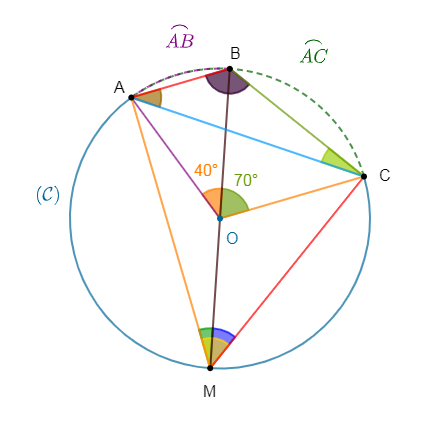
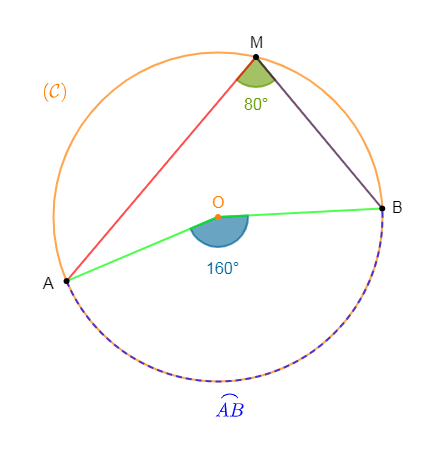
3) Si $(\mathcal{C})$ est un cercle de centre $O\ $ et $\ A\;,\ B\ $ et $\ M$ sont trois points de ce cercle tels que : $mes\;\widehat{AMB}=80^{\circ}$ alors, l'angle $\widehat{AOB}=160^{\circ}.\quad(\text{Vrai})$

En effet, $\widehat{AMB}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{AOB}.$
Donc,
$$mes\;\widehat{AOB}=2\times mes\;\widehat{AMB}$$
Par suite, $mes\;\widehat{AOB}=2\times 80^{\circ}=160^{\circ}$
D'où, $\boxed{mes\;\widehat{AOB}=160^{\circ}}$
Exercice 9 BFEM 2006 2e groupe
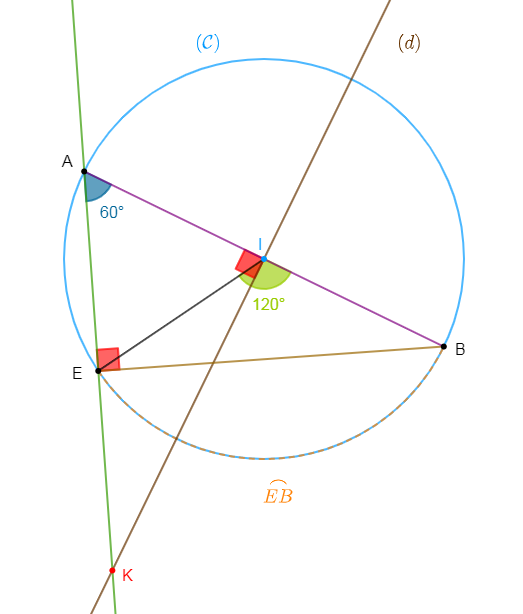
1) Traçons un cercle $(\mathcal{C})$ de centre $I$ et de diamètre $[AB]$ tel que : $AB=8\;cm$, marquons le point $E$ sur $(\mathcal{C})$ tel que : $AE=4\;cm.$
2) Déterminons la nature de chacun des triangles $ABE\ $ et $\ AEI$
$ABE$ est un triangle rectangle en $E.$
Justifions la réponse.
En effet, $ABE$ est un triangle inscrit dans le cercle $(\mathcal{C})$ et dont le côté $[AB]$ est un diamètre de ce cercle.
Par conséquent, le triangle $ABE$ est rectangle en $E.$
$AEI$ est un triangle équilatéral.
Justifions la réponse.
En effet, comme $A\ $ et $\ E$ appartiennent au cercle $(\mathcal{C})$ alors, les longueurs $IA\ $ et $\ IE$ sont égales au rayon de $(\mathcal{C}).$
Le rayon $r$ du cercle $(\mathcal{C})$ est égal à :
$$r=\dfrac{AB}{2}=\dfrac{8}{2}=4\;cm$$
Donc, $IA=IE=4\;cm$
Or, on sait que : $AE=4\;cm$
Par suite,
$$IA=IE=AE=4\,cm$$
Ainsi, le triangle $AEI$ a ses côtés de même longueur.
Par conséquent, c'est un triangle équilatéral.
3) Déterminons la mesure de chacun des angles $\widehat{EAB}\ $ et $\ \widehat{BIE}.$
En effet, d'après le résultat de la question $2)$, on a : $AEI$ est un triangle équilatéral.
Par conséquent, ses angles ont tous la même mesure de $60^{\circ}.$
D'où, $\boxed{mes\;\widehat{EAB}=60^{\circ}}$
Par ailleurs, $\widehat{EAB}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{BIE}.$
Donc,
$$mes\;\widehat{BIE}=2\times mes\;\widehat{EAB}$$
Par suite, $mes\;\widehat{BIE}=2\times 60^{\circ}=120^{\circ}$
D'où, $\boxed{mes\;\widehat{BIE}=120^{\circ}}$
4) Soit $(d)$ la médiatrice du segment $[AB]$ ; la droite $(AE)$ coupe $(d)$ en $K.$
En posant : $\cos\widehat{BAE}=\cos\widehat{KAI}$, calculons les distances $AK\ $ et $\ KI.$
En effet, $AKI$ est un triangle rectangle en $I.$
Par suite, $\cos\widehat{KAI}=\dfrac{IA}{AK}$
Or, $\cos\widehat{KAI}=\cos\widehat{BAE}\ $ et $\ \cos\widehat{BAE}=\cos 60^{\circ}=\dfrac{1}{2}$
Donc, en remplaçant $\cos\widehat{KAI}$ par $\dfrac{1}{2}$, on trouve :
$$\dfrac{1}{2}=\dfrac{IA}{AK}$$
Ce qui entraine : $AK=2\times IA$
Par suite, $AK=2\times 4=8\;cm$
D'où, $\boxed{AK=8\;cm}$
Le triangle $AKI$ étant rectangle en $I$ alors, en appliquant le théorème de Pythagore, on a :
$$KA^{2}=IA^{2}+KI^{2}$$
Ce qui entraine : $KI^{2}=KA^{2}-IA^{2}$
Par suite,
$\begin{array}{rcl} KI&=&\sqrt{KA^{2}-IA^{2}}\\\\&=&\sqrt{8^{2}-4^{2}}\\\\&=&\sqrt{64-16}\\\\&=&\sqrt{48}\\\\&=&\sqrt{16\times 3}\\\\&=&4\sqrt{3}\end{array}$
D'où, $\boxed{KI=4\sqrt{3}\;cm}$

Exercice 10
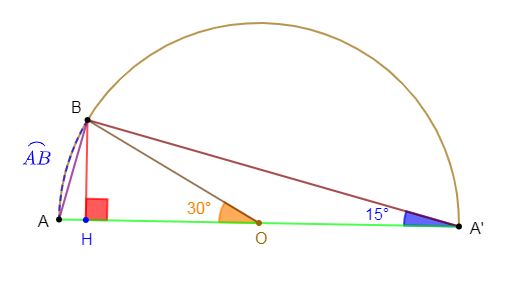
Sur un demi-cercle de diamètre $[AA']$ et de rayon $4\;cm$, plaçons le point $B$ tel que : $\widehat{AOB}=30^{\circ}$ et appelons $H$, le projeté orthogonal de $B$ sur la droite $(AA').$
1) Faisons une figure complète.

2) Calculons les longueurs : $OH\ $ et $\ HB.$
En effet, comme $H$ est le projeté orthogonal de $B$ sur la droite $(AA')$ alors, le triangle $OBH$ est rectangle en $H.$
Ainsi, $\cos\widehat{HOB}=\dfrac{OH}{OB}$
Ce qui entraine : $OH=OB\times\cos\widehat{HOB}$
Or, $\cos\widehat{HOB}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$
Donc, en remplaçant $OB\ $ et $\ \cos\widehat{HOB}$ par leur valeur, on trouve :
$$OH=4\times\dfrac{\sqrt{3}}{2}$$
D'où, $\boxed{OH=2\sqrt{3}\;cm}$
Aussi, on a : $\sin\widehat{HOB}=\dfrac{HB}{OB}$
Ce qui donne : $HB=OB\times\sin\widehat{HOB}$
Or, $\sin\widehat{HOB}=\sin 30^{\circ}=\dfrac{1}{2}$
Donc, en remplaçant $OB\ $ et $\ \sin\widehat{HOB}$ par leur valeur, on trouve :
$$HB=4\times\dfrac{1}{2}$$
Ainsi, $\boxed{HB=2\;cm}$
3) Trouvons la mesure de l'angle $\widehat{AA'B}.$
En effet, $\widehat{AA'B}$ est un angle inscrit dans ce demi-cercle et ayant pour angle au centre associé $\widehat{AOB}.$
Donc,
$$mes\;\widehat{AA'B}=\dfrac{mes\;\widehat{AOB}}{2}$$
Par suite, $mes\;\widehat{AA'B}=\dfrac{30^{\circ}}{2}=15^{\circ}$
D'où, $\boxed{mes\;\widehat{AA'B}=15^{\circ}}$
Exercice 11
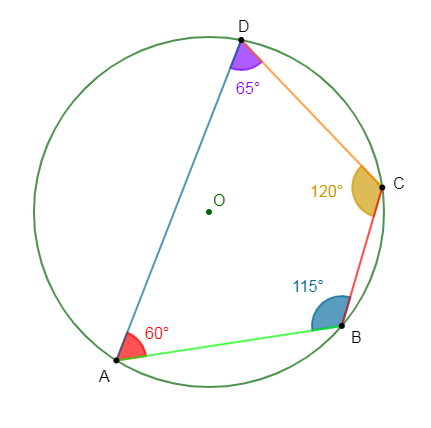
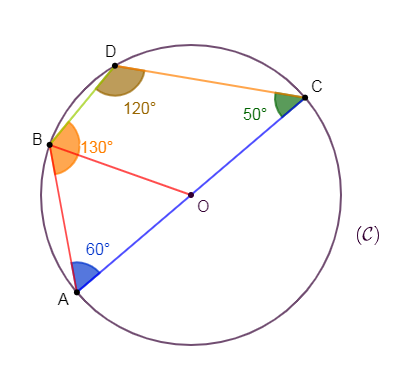
Soit $ABCD$ un quadrilatère inscriptible dans un cercle de centre $O$ et de rayon $3.5\;cm$ tel que : $mes\;\widehat{ADC}=65^{\circ}\ $ et $\ mes\;\widehat{DCB}=120^{\circ}.$
Calculons $mes\;\widehat{DAB}\ $ et $\ mes\;\widehat{ABC}.$ (On demande de faire la figure à main levée)
En effet, $ABCD$ est un quadrilatère inscriptible dans un cercle.
Or, on sait que si un quadrilatère convexe est inscriptible dans un cercle, alors les angles opposés sont supplémentaires.
Donc, les angles $\widehat{DAB}\ $ et $\ \widehat{DCB}$ sont supplémentaires.
Ce qui signifie :
$$mes\;\widehat{DAB}+mes\;\widehat{DCB}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{DAB}=180^{\circ}-mes\;\widehat{DCB}$
Alors, en remplaçant $mes\;\widehat{DCB}$ par sa valeur, on trouve :
$\begin{array}{rcl} mes\;\widehat{DAB}&=&180^{\circ}-mes\;\widehat{DCB}\\\\&=&180^{\circ}-120^{\circ}\\\\&=&60^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{DAB}=60^{\circ}}$
De la même manière, les angles $\widehat{ABC}\ $ et $\ \widehat{ADC}$ sont supplémentaires.
Ainsi,
$$mes\;\widehat{ABC}+mes\;\widehat{ADC}=180^{\circ}$$
Ce qui donne : $mes\;\widehat{ABC}=180^{\circ}-mes\;\widehat{ADC}$
En remplaçant $mes\;\widehat{ADC}$ par sa valeur, on trouve :
$\begin{array}{rcl} mes\;\widehat{ABC}&=&180^{\circ}-mes\;\widehat{ADC}\\\\&=&180^{\circ}-65^{\circ}\\\\&=&115^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{ABC}=115^{\circ}}$

Exercice 12
$(\mathcal{C})$ est un cercle de centre $O$ et de rayon $r=3\;cm\ A\;,\ B\;,\ C\ $ et $\ D$ sont quatre points de $(\mathcal{C})$ tels que : $[AC]$ est un diamètre de $(\mathcal{C})\;;\ AB=r\;,\ D$ appartient au petit arc $\overset{\displaystyle\frown}{BC}\ $ et $\ mes\;\widehat{DCA}=50^{\circ}.$
Calculons la mesure de chacun des angles du quadrilatère $ABDC.$
$-\ $ Calcul de $mes\;\widehat{BAC}$
En effet, on a : $A\ $ et $\ B$ appartiennent au cercle $(\mathcal{C}).$
Ce qui signifie que : $OA=OB=r$
Or, $AB=r$
Donc, on a :
$$AB=OA=OB$$
Ainsi, le triangle $AOB$ a ses côtés de même longueur.
Ce qui signifie que c'est un triangle équilatéral.
Par conséquent, ses angles ont la même mesure de $60^{\circ}.$
D'où, $\boxed{mes\;\widehat{BAC}=60^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{ABD}$
En effet, on remarque que $ABDC$ est un quadrilatère convexe inscriptible dans le cercle $(\mathcal{C}).$
Or, on sait que si un quadrilatère convexe est inscriptible dans un cercle, alors les angles opposés sont supplémentaires.
Donc, les angles $\widehat{ABD}\ $ et $\ \widehat{DCA}$ sont supplémentaires.
Ce qui signifie :
$$mes\;\widehat{ABD}+mes\;\widehat{DCA}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{ABD}=180^{\circ}-mes\;\widehat{DCA}$
Alors, en remplaçant $mes\;\widehat{DCA}$ par sa valeur, on trouve :
$\begin{array}{rcl} mes\;\widehat{ABD}&=&180^{\circ}-mes\;\widehat{DCA}\\\\&=&180^{\circ}-50^{\circ}\\\\&=&130^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{ABD}=130^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{BDC}$
De la même manière, les angles $\widehat{BDC}\ $ et $\ \widehat{BAC}$ sont supplémentaires.
Ce qui signifie :
$$mes\;\widehat{BDC}+mes\;\widehat{BAC}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{BDC}=180^{\circ}-mes\;\widehat{BAC}$
Alors, en remplaçant $mes\;\widehat{BAC}$ par sa valeur, on trouve :
$\begin{array}{rcl} mes\;\widehat{BDC}&=&180^{\circ}-mes\;\widehat{BAC}\\\\&=&180^{\circ}-60^{\circ}\\\\&=&120^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{BDC}=120^{\circ}}$

Exercice 13
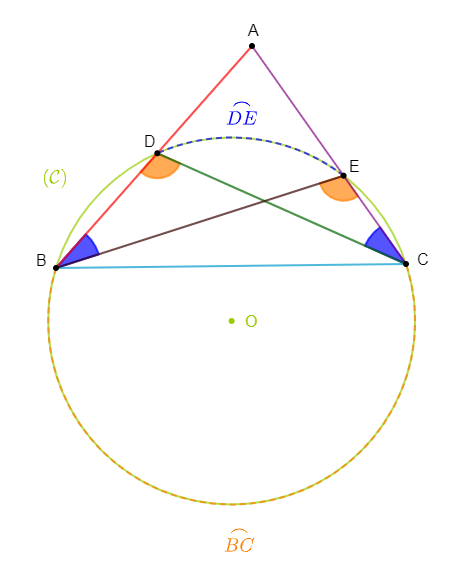
Soit $ABC$ un triangle.
$(\mathcal{C})$ est un cercle de centre $O$ passant par $B$ et par $C$ et recoupant le segment $[AB]$ en $D$ et le segment $[AC]$ en $E.$
1) Faisons une figure.

2) Montrons que : $mes\;\widehat{BDC}=mes\;\widehat{CEB}$ et que : $mes\;\widehat{EBA}=mes\;\widehat{DCA}.$
En effet, nous constatons que $\widehat{BDC}\ $ et $\ \widehat{CEB}$ sont deux angles inscrits dans $(\mathcal{C})$ et interceptant le même arc de cercle $\overset{\displaystyle\frown}{BC}.$
Or, dans un cercle, deux angles inscrits interceptant le même arc ont la même mesure.
Donc, les angles $\widehat{BDC}\ $ et $\ \widehat{CEB}$ ont la même mesure.
D'où, $\boxed{mes\;\widehat{BDC}=mes\;\widehat{CEB}}$
De la même manière, nous remarquons que $\widehat{EBA}\ $ et $\ \widehat{DCA}$ sont deux angles inscrits dans $(\mathcal{C})$ et interceptant le même arc de cercle $\overset{\displaystyle\frown}{DE}.$
Par conséquent, ils ont la même mesure.
D'où, $\boxed{mes\;\widehat{EBA}=mes\;\widehat{DCA}}$
Exercice 14
Définissons les expressions suivantes :
$-\ $ Angle inscrit : on appelle angle inscrit dans un cercle, un angle dont le sommet est un point du cercle et ses côtés recoupent le cercle
$-\ $ Angle au centre : on appelle angle au centre, un angle dont le sommet est le centre d'un cercle.
$-\ $ Angles associés : deux angles sont dits associés s'ils sont liés par une relation particulière.
Exemple :
l'angle inscrit et l'angle au centre interceptant le même arc sont associés.
deux angles complémentaires sont associés
deux angles supplémentaires sont associés
Exercice 15
Les angles cités dans le tableau sont des angles inscrits dans le cercle $\mathcal{C}(O\;;\ r)$ sauf l'angle $\widehat{DAF}.$
Déterminons l'arc intercepté et nommons l'angle au centre associé.
Recopions et complétons le tableau.

$$\begin{array}{|c|c|c|c|}\hline\text{Angles}&\text{Inscrit (oui/non)}&\text{Arc intercepté}&\text{Angle au centre associé}\\ \hline\widehat{EDF}&\text{oui}&\overset{\displaystyle\frown}{FE}&\widehat{EOF}\\ \hline\widehat{ADE}&\text{oui} &\overset{\displaystyle\frown}{CE}&\widehat{COE}\\ \hline\widehat{DAF}&\text{non}&&\\ \hline\widehat{BFA}&\text{oui}&\overset{\displaystyle\frown}{BE}&\widehat{BOE}\\ \hline\widehat{DEF}&\text{oui}&\overset{\displaystyle\frown}{DF}&\widehat{DOF}\\ \hline\end{array}$$
Exercice 16
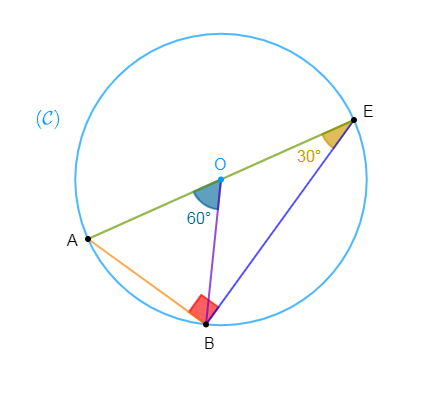
Construisons un cercle $\mathcal{C}(O\;;\ r)$ et marquons sur $(\mathcal{C})$ les points $A\;,\ B\ $ et $\ E$ tels que $A\ $ et $\ E$ soient diamétralement opposés et $\widehat{AEB}=30^{\circ}.$

1) Calculons l'angle $\widehat{AOB}.$
En effet, $\widehat{AEB}$ est un angle inscrit dans $(\mathcal{C})$ et ayant pour angle au centre associé $\widehat{AOB}.$
Donc,
$$mes\;\widehat{AOB}=2\times mes\;\widehat{AEB}$$
Par suite, $mes\;\widehat{AOB}=2\times 30^{\circ}=60^{\circ}$
D'où, $\boxed{mes\;\widehat{AOB}=60^{\circ}}$
2) Montrons que le triangle $AOB$ est équilatéral.
En effet, on a : $A\ $ et $\ B$ appartiennent au cercle $\mathcal{C}(O\;;\ r).$
Ce qui signifie que : $\boxed{OA=OB=r}$
D'où, le triangle $AOB$ est isocèle en $O.$
De plus, d'après le résultat de la question $1)$, on a : $mes\;\widehat{AOB}=60^{\circ}.$
Ainsi, le triangle isocèle $AOB$ a un angle de $60^{\circ}.$
Or, on sait que si un triangle isocèle a un angle de $60^{\circ}$ alors, c'est un triangle équilatéral.
Par conséquent, d'après cette propriété, $AOB$ est un triangle équilatéral.
Exercice 17
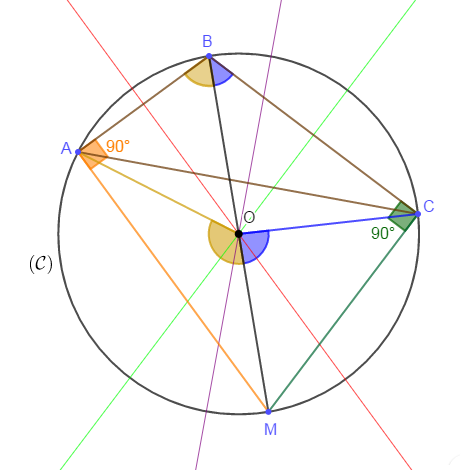
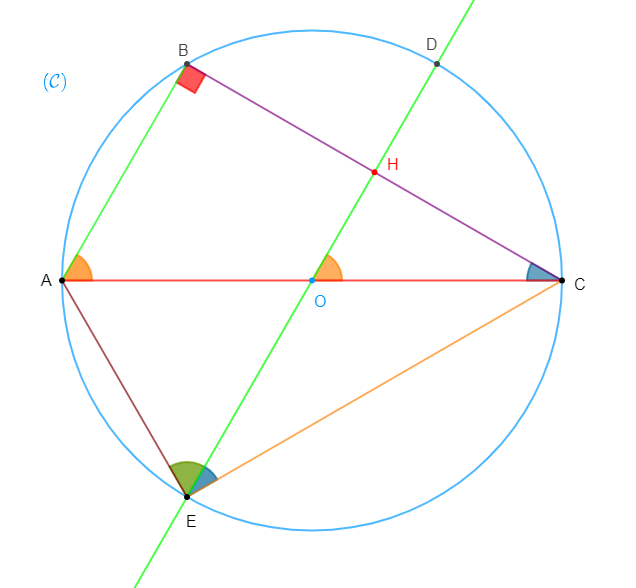
Construisons un triangle $ABC$ puis traçons le cercle $(\mathcal{C})$ circonscrit à ce triangle.
Soit $O$ le centre de ce cercle et $M$ le symétrique de $B$ par rapport à $O.$

En effet, $O$ est le point de rencontre des trois médiatrices respectives des côtés du triangle $ABC.$
De plus, les points $M\;;\ O\ $ et $\ B$ sont alignés et $[BM]$ est un diamètre de $(\mathcal{C}).$
1) a) Donnons la relation entre les mesures des angles suivants :
$\centerdot\ \widehat{MOC}\ $ et $\ \widehat{MBC}.$
On a : $\widehat{MBC}$ étant un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{MOC}$ alors,$$\boxed{mes\;\widehat{MOC}=2\times mes\;\widehat{MBC}}$$
$\centerdot\ \widehat{MOA}\ $ et $\ \widehat{MBA}.$
De la même manière, $\widehat{MBA}$ est un angle inscrit dans $(\mathcal{C})$ ayant pour angle au centre associé $\widehat{MOA}$ donc,$$\boxed{mes\;\widehat{MOA}=2\times mes\;\widehat{MBA}}$$
b) Déduisons-en $\widehat{ABC}$ en fonction de $\widehat{AOC}$
On a : $mes\;\widehat{AOC}=mes\;\widehat{MOA}+mes\;\widehat{MOC}$
Or, $mes\;\widehat{MOA}=2\times mes\;\widehat{MBA}\ $ et $\ mes\;\widehat{MOC}=2\times mes\;\widehat{MBC}$
Donc, en remplaçant dans l'expression de $mes\;\widehat{AOC}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{AOC}&=&mes\;\widehat{MOA}+mes\;\widehat{MOC}\\\\&=&2\times mes\;\widehat{MBA}+2\times mes\;\widehat{MBC}\\\\&=&2\times\left(mes\;\widehat{MBA}+mes\;\widehat{MBC}\right)\end{array}$
Par suite, $mes\;\widehat{AOC}=2\times\left(mes\;\widehat{MBA}+mes\;\widehat{MBC}\right)$
Comme $mes\;\widehat{MBA}+mes\;\widehat{MBC}=mes\;\widehat{ABC}$ alors, $mes\;\widehat{AOC}=2\times mes\;\widehat{ABC}$
D'où, $$\boxed{mes\;\widehat{ABC}=mes\;\dfrac{\widehat{AOC}}{2}}$$
2) a) Comparons $\widehat{BAM}\ $ et $\ \widehat{BCM}.$
On sait que les arcs $\overset{\displaystyle\frown}{BM}\ $ et $\ \overset{\displaystyle\frown}{MB}$ sont deux demi-cercles de $(\mathcal{C})$ donc, ils sont de même longueur.
Or, $\widehat{BAM}\ $ et $\ \widehat{BCM}$ sont deux angles inscrits dans le cercle et interceptant respectivement les arcs $\overset{\displaystyle\frown}{BM}\ $ et $\ \overset{\displaystyle\frown}{MB}$ qui sont de même longueur.
Donc, les angles $\widehat{BAM}\ $ et $\ \widehat{BCM}$ ont la même mesure.
D'où, $$\boxed{mes\;\widehat{BAM}=mes\;\widehat{BCM}}$$
b) Déduisons-en la nature de chacun des triangles $ABM\ $ et $\ MCB.$
On a : $\widehat{BAM}$ est un angle inscrit dans $(\mathcal{C})$ et ayant pour angle au centre associé $\widehat{MOB}$ donc, $mes\;\widehat{BAM}=\dfrac{mes\;\widehat{MOB}}{2}$
Or, $\widehat{MOB}$ est un angle plat donc, $mes\;\widehat{MOB}=180^{\circ}$
Par suite, $mes\;\widehat{BAM}=\dfrac{180^{\circ}}{2}=90^{\circ}$
D'où, $ABM$ est un triangle rectangle en $A.$
Par ailleurs, d'après question 2)a), les angles $\widehat{BAM}\ $ et $\ \widehat{BCM}$ ont la même mesure.
Or, $mes\;\widehat{BAM}=90^{\circ}$ donc, $mes\;\widehat{BCM}=90^{\circ}$
Ainsi, $MCB$ est un triangle rectangle en $C.$
Exercice 18
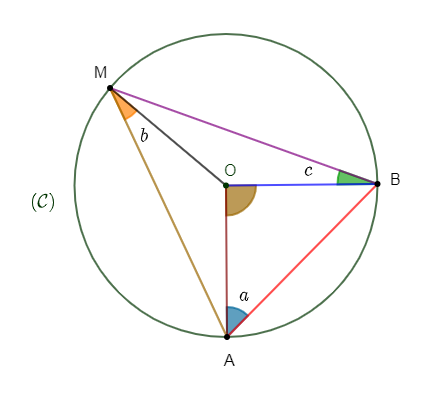
On considère un cercle $(\mathcal{C})$ de centre $O$ et $A\;,\ M\ $ et $\ B$ trois points distincts de $(\mathcal{C})$ non diamétralement opposés deux à deux.
1) Justifions que les triangles $AOB\;,\ AOM\ $ et $\ BOM$ sont isocèles.
En effet, comme $A\;,\ M\ $ et $\ B$ sont trois points distincts de $(\mathcal{C})$ non diamétralement opposés deux à deux alors, on a :
$OA=OB$ ce qui justifie que le triangle $AOB$ est isocèle en $O$
$OA=OM$ ce qui prouve que le triangle $AOM$ est isocèle en $O$
$OB=OM$ ce qui signifie que le triangle $BOM$ est isocèle en $O$
2) Exprimons la mesure de l'angle $\widehat{AOB}$ en fonction de la mesure de l'angle $\widehat{OAB}.$
En effet, on sait que la somme des angles d'un triangle est égale à $180^{\circ}.$
Donc,
$$mes\;\widehat{AOB}+mes\;\widehat{OAB}+mes\;\widehat{OBA}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{AOB}=180^{\circ}-mes\;\widehat{OAB}-mes\;\widehat{OBA}$
Or, le triangle $AOB$ est isocèle en $O$ donc, les angles $\widehat{OAB}\ $ et $\ \widehat{OBA}$ ont la même mesure.
C'est-à-dire ; $mes\;\widehat{OAB}=mes\;\widehat{OBA}.$
Par suite, en remplaçant $mes\;\widehat{OBA}=mes\;\widehat{OAB}$, on obtient :
$$mes\;\widehat{AOB}=180^{\circ}-mes\;\widehat{OAB}-mes\;\widehat{OAB}$$
D'où, $\boxed{mes\;\widehat{AOB}=180^{\circ}-2\,mes\;\widehat{OAB}}$
3) On note $\widehat{OAB}=a\;;\ \widehat{OMA}=b\ $ et $\ \widehat{OBM}=c.$
a) Exprimons la somme des angles du triangle $AMB$ en fonction de $a\;,\ b\ $ et $\ c.$
On a :
$\widehat{BMA}=\widehat{BMO}+\widehat{OMA}=b+c$
$\widehat{ABM}=\widehat{ABO}+\widehat{OBM}=a+c$
$\widehat{MAB}=\widehat{MAO}+\widehat{OAB}=b+a$
Alors,
$\begin{array}{rcl} \widehat{BMA}+\widehat{ABM}+\widehat{MAB}&=&(b+c)+(a+c)+(b+a)\\\\&=&b+c+a+c+b+a\\\\&=&2a+2b+2c\end{array}$
D'où, $\boxed{\widehat{BMA}+\widehat{ABM}+\widehat{MAB}=2a+2b+2c}$
b) En utilisant la propriété de la somme des angles dans un triangle, exprimons $2a$ en fonction de $b\ $ et $\ c.$
En effet, on sait que la somme des angles d'un triangle est égale à $180^{\circ}.$
Donc,
$$\widehat{BMA}+\widehat{ABM}+\widehat{MAB}=180^{\circ}$$
C'est-à-dire ; $2a+2b+2c=180^{\circ}$
Ce qui entraine : $\boxed{2a=180^{\circ}-2b-2c}$
c) Déduisons du $b)$ et du $2)$ l'expression de l'angle $\widehat{AOB}$ en fonction $b\ $ et $\ c.$
D'après le résultat de la question $2)$, on a :
$$mes\;\widehat{AOB}=180^{\circ}-2\,mes\;\widehat{OAB}=180^{\circ}-2a$$
Or, d'après $b)$, on a : $2a=180^{\circ}-2b-2c$
Donc, en remplaçant $2a$ par son expression, on trouve :
$\begin{array}{rcl} mes\;\widehat{AOB}&=&180^{\circ}-2a\\\\&=&180^{\circ}-(180^{\circ}-2b-2c)\\\\&=&180^{\circ}-180^{\circ}+2b+2c\\\\&=&2b+2c\end{array}$
Ainsi, $\boxed{mes\;\widehat{AOB}=2b+2c}$
d) Déduisons, en factorisant par $2$, l'expression de l'angle $\widehat{AOB}$ en fonction de l'angle inscrit $M.$
On a : $mes\;\widehat{AOB}=2b+2c=2(b+c)$
Or, $mes\;\widehat{BMA}=b+c$
Donc, $\boxed{mes\;\widehat{AOB}=2\times mes\;\widehat{BMA}}$

Exercice 19
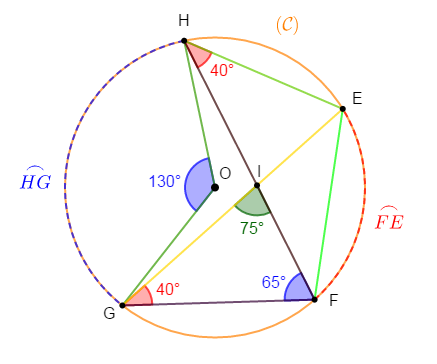
Sur la figure ci-dessous, les points $E\;,\ F\;,\ G\ $ et $\ H$ sont sur le cercle $(\mathcal{C})$ de centre $O.$

Les droites $(FH)\ $ et $\ (EG)$ sont sécantes au point $I.$
$\widehat{HOG}=130^{\circ}\ $ et $\ \widehat{EHF}=40^{\circ}$
Calculons la mesure de chaque angle du triangle $FGI$ en justifiant chaque réponse.
On a : $\widehat{FGI}\ $ et $\ \widehat{EHF}$ sont deux angles inscrits dans le cercle $(\mathcal{C})$ et interceptant le même arc $\overset{\displaystyle\frown}{FE}.$
Donc, $\widehat{FGI}\ $ et $\ \widehat{EHF}$ sont de même mesure.
Or, $\widehat{EHF}=40^{\circ}$
Par conséquent, $\boxed{\widehat{FGI}=40^{\circ}}$
Par ailleurs, $\widehat{IFG}$ est un angle inscrit dans $(\mathcal{C})$ et ayant pour angle au centre associé $\widehat{HOG}$ donc, $\widehat{IFG}=\dfrac{\widehat{HOG}}{2}$
Or, $\widehat{HOG}=130^{\circ}$
Donc, $\widehat{IFG}=\dfrac{130^{\circ}}{2}=65^{\circ}$
Par suite, $\boxed{\widehat{IFG}=65^{\circ}}$
Ainsi, comme la somme des angles d'un triangle est égale à $180^{\circ}.$
Donc, pour le triangle $FGI$, on a :
$$\widehat{FGI}+\widehat{IFG}+\widehat{GIF}=180^{\circ}$$
D'où,
$\begin{array}{rcl}\widehat{GIF}&=&180^{\circ}-(\widehat{FGI}+\widehat{IFG})\\\\&=&180^{\circ}-(40^{\circ}+65^{\circ})\\\\&=&180^{\circ}-105^{\circ}\\\\&=&75^{\circ}\end{array}$
Par conséquent, $\boxed{\widehat{GIF}=75^{\circ}}$
Exercice 20
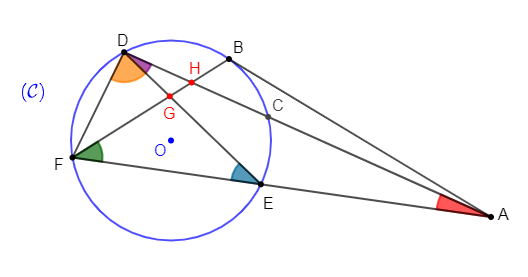
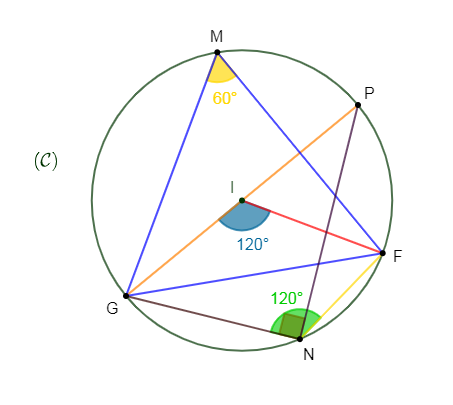
On considère la figure ci-dessous dans laquelle :

Les points $P\;,\ F\;,\ N\;,\ M\ $ et $\ G$ appartiennent au cercle de centre $I.$
Le segment $[GP]$ est un diamètre du cercle et le point $F$ appartient à la médiatrice de $[MG]$
1) Déterminons la nature du triangle $GNP$
$GPN$ est un triangle inscrit dans le cercle et dont le côté $[GP]$ est un diamètre de ce cercle.
Par conséquent, c'est un triangle rectangle en $N.$
2) Démontrons que le triangle $MGF$ est un triangle équilatéral.
En effet, comme $F$ appartient à la médiatrice de $[MG]$ alors, $F$ est équidistant des extrémités $M\ $ et $\ G$ de ce segment.
Ce qui veut dire :
$$FG=FM$$
Ainsi, le triangle $MGF$ est isocèle en $F.$
Par ailleurs, $\widehat{GMF}$ est un angle inscrit dans $(\mathcal{C})$ et ayant pour angle au centre associé $\widehat{GIF}.$
Donc, on a :
$$mes\;\widehat{GMF}=\dfrac{mes\;\widehat{GIF}}{2}$$
Or, $mes\;\widehat{GIF}=120^{\circ}$
Donc, $mes\;\widehat{GMF}=\dfrac{120^{\circ}}{2}=60^{\circ}$
Par suite, $\boxed{mes\;\widehat{GMF}=60^{\circ}}$
Ainsi, le triangle isocèle $MGF$ a un angle de $60^{\circ}.$
Or, on sait que si un triangle isocèle a un angle de $60^{\circ}$ alors, c'est un triangle équilatéral.
Par conséquent, d'après cette propriété, $MGF$ est un triangle équilatéral.
3) Calculons la mesure de l'angle $\widehat{GNF}.$
En effet, nous remarquons que $MGNF$ est un quadrilatère convexe inscriptible dans le cercle $(\mathcal{C}).$
Or, on sait que si un quadrilatère convexe est inscriptible dans un cercle, alors les angles opposés sont supplémentaires.
Donc, les angles $\widehat{GNF}\ $ et $\ \widehat{GMF}$ sont supplémentaires.
Ce qui signifie :
$$mes\;\widehat{GNF}+mes\;\widehat{GMF}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{GNF}=180^{\circ}-mes\;\widehat{GMF}$
Alors, en remplaçant $mes\;\widehat{GMF}$ par sa valeur, on trouve :
$\begin{array}{rcl} mes\;\widehat{GNF}&=&180^{\circ}-mes\;\widehat{GMF}\\\\&=&180^{\circ}-60^{\circ}\\\\&=&120^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{GNF}=120^{\circ}}$
Exercice 21
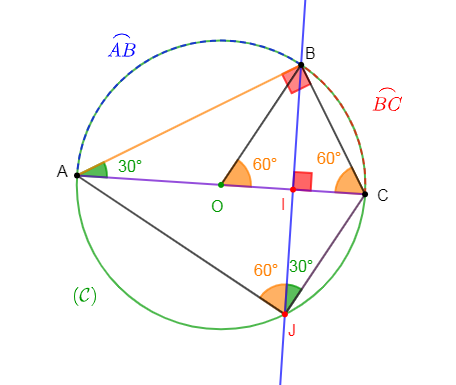
$ABC$ est un triangle rectangle en $B$ tel que $AB=5\;cm\;;\ \widehat{BAC}=30^{\circ}.$
1) Construisons $ABC.$
2) Construisons le cercle circonscrit au triangle $ABC$ son centre est $O.$
3) La hauteur $(BI)$ de $ABC$ coupe $(AC)$ en $I$ et le cercle en $J.$
Déterminons $\widehat{BJC}$
En effet, $\widehat{BJC}\ $ et $\ \widehat{BAC}$ sont deux angles inscrits dans le cercle $(\mathcal{C})$ interceptant le même arc de cercle $\overset{\displaystyle\frown}{BC}.$
Ils ont alors la même mesure.
D'où, $\boxed{mes\;\widehat{BJC}=30^{\circ}}$
4) Calculons les mesures des angles du triangle $BOC$
On a : $\widehat{BAC}$ est un angle inscrit dans le cercle $(\mathcal{C})$ et ayant pour angle au centre associé $\widehat{BOC}.$
Alors, on a :
$$mes\;\widehat{BOC}=2\times mes\;\widehat{BAC}$$
Or, $mes\;\widehat{BAC}=30^{\circ}$
Donc, $mes\;\widehat{BOC}=2\times 30^{\circ}=60^{\circ}$
D'où, $\boxed{mes\;\widehat{BOC}=60^{\circ}}$
Par ailleurs, on a : $OB=OC.$
Ce qui signifie que le triangle $AOB$ est isocèle en $O.$
Donc, le triangle isocèle $AOB$ a un angle de $60^{\circ}.$
Ainsi, $AOB$ est un triangle isocèle qui a un angle de $60^{\circ}$ donc, c'est un triangle équilatéral.
Par conséquent, ses angles ont la même mesure de $60^{\circ}.$
D'où, $\boxed{mes\;\widehat{OBC}=mes\;\widehat{BCO}=60^{\circ}}$
5) Calculons les mesures des angles du triangle $ABJ.$
En effet, $\widehat{BCA}\ $ et $\ \widehat{BJA}$ sont deux angles inscrits dans le cercle $(\mathcal{C})$ interceptant le même arc de cercle $\overset{\displaystyle\frown}{AB}.$
Ils ont alors la même mesure.
Or, $mes\;\widehat{BCA}=mes\;\widehat{BCO}=60^{\circ}$
Donc, $\boxed{mes\;\widehat{BJA}=60^{\circ}}$
Par ailleurs, comme le diamètre $[AC]$ est perpendiculaire à la corde $[BJ]$ alors, $(AC)$ est médiatrice du segment $[BJ].$
Par suite, $AB=AJ$
D'où, le triangle $ABJ$ est isocèle en $A.$
Ainsi, $ABJ$ est un triangle isocèle qui a un angle de $60^{\circ}$ donc, c'est un triangle équilatéral.
Par conséquent, ses angles ont la même mesure de $60^{\circ}.$
D'où, $\boxed{mes\;\widehat{ABJ}=mes\;\widehat{BAJ}=60^{\circ}}$

Exercice 22
On considère la figure ci-dessous

où le cercle de centre $O$ a pour diamètre $AC=10\;cm$ ;
$B$ sur le cercle tel que $AB=5\;cm.$
1) Déterminons la nature du triangle $ABC$
$ABC$ est un triangle rectangle en $B.$
Justifions notre réponse.
En effet, $ABC$ est un triangle inscrit dans le cercle et dont le côté $[AC]$ est un diamètre de ce cercle.
Par conséquent, c'est un triangle rectangle en $B.$
2) Calculons la valeur exacte de la distance $BC.$
Comme $ABC$ est rectangle en $B$ alors, d'après le théorème de Pythagore, on a :
$$BC^{2}+AB^{2}=AC^{2}$$
Cela donne : $BC^{2}=AC^{2}-AB^{2}$
Par suite,
$\begin{array}{rcl} BC&=&\sqrt{AC^{2}-AB^{2}}\\\\&=&\sqrt{10^{2}-5^{2}}\\\\&=&\sqrt{100-25}\\\\&=&\sqrt{75}\\\\&=&\sqrt{25\times 3}\\\\&=&5\sqrt{3}\end{array}$
D'où, $\boxed{BC=5\sqrt{3}\;cm}$
3) Calculons la mesure de l'angle $\widehat{ACB}.$
Comme $ABC$ est rectangle en $B$ alors, en utilisant le sinus de l'angle $\widehat{ACB}$, on obtient :
$$\sin\widehat{ACB}=\dfrac{AB}{AC}=\dfrac{5}{10}=\dfrac{1}{2}$$
Or, on sait que l'angle de mesure $30^{\circ}$ a pour sinus $\dfrac{1}{2}.$
Donc, $\boxed{mes\;\widehat{ACB}=30^{\circ}}$
4) La parallèle à la droite $(AB)$ passant par $O$ coupe le segment $[BC]$ en $H$ et le cercle en deux points $D$ et $E$ tels que $CD<CE.$
a) Calculons la mesure de l'angle $\widehat{HOC}.$
En effet, les parallèles $(AB)\ $ et $\ (OH)$ coupées par la sécante $(AC)$ déterminent deux angles $\widehat{HOC}\ $ et $\ \widehat{BAC}$ correspondants.
Or, on sait que deux droites parallèles coupées par une sécante déterminent deux angles correspondants de même mesure.
Par conséquent, les angles $\widehat{HOC}\ $ et $\ \widehat{BAC}$ ont la même mesure.
Déterminons alors la mesure de l'angle $\widehat{BAC}.$
On sait que dans un triangle rectangle, les angles aigus sont complémentaires.
Donc, dans le triangle $ABC$, on a :
$$mes\;\widehat{BAC}+mes\;\widehat{ACB}=90^{\circ}$$
Ce qui entraine : $mes\;\widehat{BAC}=90^{\circ}-mes\;\widehat{ACB}$
En remplaçant $mes\;\widehat{ACB}$ par sa valeur, on trouve :
$$mes\;\widehat{BAC}=90^{\circ}-30^{\circ}=60^{\circ}$$
Par conséquent, $\boxed{mes\;\widehat{HOC}=60^{\circ}}$
b) Déduisons-en la mesure de l'angle $\widehat{DEC}$ et celle de l'angle $\widehat{DEA}.$
En effet, $\widehat{DEC}$ est un angle inscrit dans le cercle et ayant pour angle au centre associé $\widehat{HOC}.$
Donc, on a :
$$mes\;\widehat{DEC}=\dfrac{mes\;\widehat{HOC}}{2}$$
Or, d'après le résultat de la question $a)$, on a : $mes\;\widehat{HOC}=60^{\circ}$
Donc, $mes\;\widehat{DEC}=\dfrac{60^{\circ}}{2}=30^{\circ}$
Ainsi, $\boxed{mes\;\widehat{DEC}=30^{\circ}}$
En effet, les angles $\widehat{DEC}\ $ et $\ \widehat{DEA}$ sont adjacents complémentaires.
Donc,
$$mes\;\widehat{DEA}+mes\;\widehat{DEC}=90^{\circ}$$
Ce qui entraine : $mes\;\widehat{DEA}=90^{\circ}-mes\;\widehat{DEC}$
En remplaçant $mes\;\widehat{DEC}$ par sa valeur, on trouve :
$$mes\;\widehat{DEA}=90^{\circ}-30^{\circ}=60^{\circ}$$
D'où, $\boxed{mes\;\widehat{DEA}=60^{\circ}}$
Exercice 23
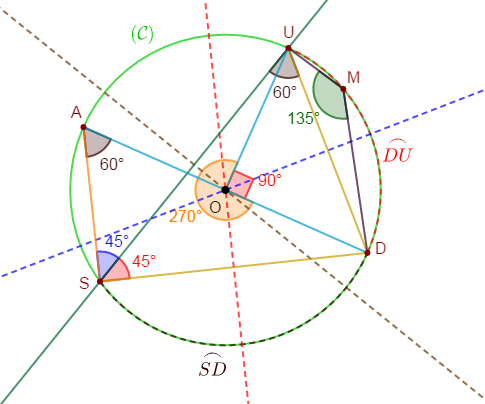
Soit $SUD$ un triangle tel que
$$SU=6\;cm\;;\ \widehat{SUD}=60^{\circ}\ \text{ et }\ \widehat{DSU}=45^{\circ}$$
$(\mathcal{C})$ est le cercle de centre $O$ circonscrit au triangle $SUD.$
1) Faisons une figure.
Le point $O$ centre du cercle $(\mathcal{C})$ est le point de rencontre des trois médiatrices des côtés du triangle $SUD.$

2) Montrons que $\widehat{UOD}=90^{\circ}$
$\widehat{DSU}$ est un angle inscrit dans $(\mathcal{C})$ et ayant pour angle au centre associé $\widehat{UOD}$ donc, $\widehat{UOD}=2\times\widehat{DSU}$
Or, $\widehat{DSU}=45^{\circ}$
Donc, $\widehat{UOD}=2\times 45^{\circ}=90^{\circ}$
Ainsi, $$\boxed{\widehat{UOD}=90^{\circ}}$$
3) Soit $A$ le point diamétralement opposé à $D.$
a) Calculons $\widehat{SAD}.$
On remarque que $\widehat{SAD}\ $ et $\ \widehat{SUD}$ sont deux angles inscrits dans le cercle $(\mathcal{C})$ et interceptant le même arc $\overset{\displaystyle\frown}{SD}.$
Donc, $\widehat{SAD}\ $ et $\ \widehat{SUD}$ sont de même mesure.
Or, $\widehat{SUD}=60^{\circ}$
Par conséquent, $$\boxed{\widehat{SAD}=60^{\circ}}$$
b) Montrons que $(SU)$ est la bissectrice de $\widehat{DSA}$
En effet, $SAD$ est un triangle inscrit dans le cercle $(\mathcal{C})$ et dont le côté $[AD]$ est diamètre.
Donc, $SAD$ est un triangle rectangle en $S.$
Par suite, $\widehat{DSA}=90^{\circ}$
Ainsi,
$\begin{array}{rcl}\widehat{USA}&=&\widehat{DSA}-\widehat{DSU}\\\\&=&90^{\circ}-45^{\circ}\\\\&=&45^{\circ}\end{array}$
D'où, $$\boxed{\widehat{USA}=45^{\circ}}$$
Ce qui montre alors que $\widehat{DSU}\ $ et $\ \widehat{USA}$ sont deux angles adjacents de même mesure.
Par conséquent, la droite $(SU)$ est la bissectrice de l'angle $\widehat{DSA}.$
4) Soit $M$ un point de l'arc $\overset{\displaystyle\frown}{DU}$
a) L'angle au centre associé à $\widehat{DMU}$ est l'angle $\check{UOD}.$
b) En déduisons la mesure de l'angle $\widehat{DMU}.$
On a : $\widehat{DMU}$ est un angle inscrit dans $(\mathcal{C})$ et ayant pour angle au centre associé $\check{UOD}.$
Donc, $mes\;\widehat{DMU}=\dfrac{mes\;\check{UOD}}{2}$
Or,
$\begin{array}{rcl}\check{UOD}&=&360^{\circ}-\widehat{UOD}\\\\&=&360^{\circ}-90^{\circ}\\\\&=&270^{\circ}\end{array}$
Donc, $\boxed{\check{UOD}=270^{\circ}}$
Par suite, $mes\;\widehat{DMU}=\dfrac{270^{\circ}}{2}=135^{\circ}$
D'où, $$\boxed{mes\;\widehat{DMU}=135^{\circ}}$$
Exercice de Synthèse
L'angle inscrit est égal :
b) $\dfrac{1}{2}$ angle au centre
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
ven, 05/15/2020 - 11:58
Permalien
la suite?????
Penda (non vérifié)
sam, 03/06/2021 - 12:53
Permalien
Faire mes exercices
Anonyme (non vérifié)
dim, 04/24/2022 - 20:15
Permalien
Comment peut on faire pour
Coura séné (non vérifié)
mar, 03/23/2021 - 20:23
Permalien
Comment résoudre l'exercice 6
omar diakhate (non vérifié)
lun, 04/26/2021 - 12:12
Permalien
la suite
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 03:09
Permalien
Correction d exercice n19
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 03:12
Permalien
Correction
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 03:12
Permalien
Correction
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 03:12
Permalien
Correction
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 03:12
Permalien
Correction
MOUHAMED ndiaye (non vérifié)
mar, 05/04/2021 - 03:12
Permalien
Correction
Idk (non vérifié)
mar, 10/19/2021 - 10:11
Permalien
google.com && echo "Haxxed"
Mouhamed Ba (non vérifié)
mar, 04/19/2022 - 01:31
Permalien
24 2 8
mayé faye (non vérifié)
mar, 01/17/2023 - 23:26
Permalien
merci infiniment à l'auteur
mayé faye (non vérifié)
mar, 01/17/2023 - 23:26
Permalien
merci infiniment à l'auteur
Ajouter un commentaire