Fonctions scalaires et vectorielles de Leibniz - T S1
I Barycentre
Soient $(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$, $\ n$ points pondérés ; $\alpha_{i}\in\mathbb{R}\;,\ \ A_{i}\in$ l'espace $\mathbf{E}.$ On appelle barycentre de $(A_{i}\;,\ \alpha_{i})$ l'unique point $G$ vérifiant :
$$\alpha_{1}\overrightarrow{GA}_{1}+\alpha_{2}\overrightarrow{GA}_{2}+\ldots+\alpha_{n}\overrightarrow{GA}_{n}=\vec{0}$$ avec $\sum_{i=1}^{n} \alpha_{i} \neq 0$
I.1 Propriétés
$\centerdot\ \ $ Propriété caractéristique : $G$ barycentre de $(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$, si et seulement si, $$\forall\;M\in\mathbf{E}\;,\ \sum_{i=1}^{n}\alpha_{i}\overrightarrow{MA}_{i}=\left(\sum_{i=1}^{n} \alpha_{i}\right)\overrightarrow{MG}$$
et $\sum_{i=1}^{n} \alpha_{i} \neq 0$.
Donc dans le repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$ on a : \begin{eqnarray}\sum_{i=1}^{n}\alpha_{i}\overrightarrow{OA}_{i}&=&(\sum_{i=1}^{n} \alpha_{i})\overrightarrow{OG}\nonumber \\ \Rightarrow\ \overrightarrow{OG}&=&\frac{1}{\sum_{i=1}^{n} \alpha_{i}}\left(\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}\right)\nonumber \end{eqnarray}
$$\Rightarrow G\begin{pmatrix}\dfrac{1}{\sum_{i=1}^{n} \alpha_{i}}(\alpha_{1}x_{1}+\alpha_{2}x_{2}+\ldots+\alpha_{n}x_{n})\\ \\ \dfrac{1}{\sum_{i=1}^{n} \alpha_{i}}(\alpha_{1}y_{1}+\alpha_{2}y_{2}+\ldots+\alpha_{n}y_{n})\end{pmatrix}$$
Aussi nous obtenons dans le repère $(O\;;\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ :
$$z_{G}=\dfrac{\alpha_{1}z_{A_{1}}+\alpha_{2}z_{A_{2}}+\ldots+\alpha_{n}z_{A_{n}}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$.
$$z_{G}=\dfrac{\alpha_{1}z_{A_{1}}+\alpha_{2}z_{A_{2}}+\ldots+\alpha_{n}z_{A_{n}}}{\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n}}$$.
$\centerdot\ \ G$ barycentre de $(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$ $\Leftrightarrow$ $\forall\;k\in \mathbb{R}^{*}\;$, $\ G$ barycentre de $(A_{i}\;,\ k\alpha_{i})_{1\leq i\leq n}.$ Le barycentre reste inchangé si on multiplie les coefficients par un même réel $k\neq 0.$
$\centerdot\ \ $ Barycentre partiel :
Soit $G$ barycentre de $(A_{i}\;,\ \alpha_{i})_{i\in\mathbf{I}}\;, \: \mathbf{I}\subset\mathbb{N}$.
Si $G_{1}$ est barycentre de $(A_{i}\;,\ \alpha_{i})_{i\in\mathbf{I}'}\;, \: \mathbf{I}'\subset\mathbf{I}$ alors $G$ sera barycentre de
$$\left\lbrace\left(G_{1}\;,\ \left(\sum\alpha_{i}\right)_{i\in\mathbf{I'}}\right)\;; \: (A_{i},\ \alpha_{i})_{i\in(\mathbf{I}\setminus\mathbf{I'})}\right\rbrace$$
$\centerdot\ \ $ Remarques :
Soit $G$ barycentre de $(A_{i}\;,\ \alpha_{i})_{i\in\mathbf{I}}\;, \: I\subset\mathbb{N}$.
Si $\forall\;i\;,\ j \quad \alpha_{i}=\alpha_{j}$, on dira alors que $G$ est isobarycentre de $A_{i}\;,\ \: i\in\mathbf{I}$.
$\centerdot\ \ $ L'isobarycentre de deux points est leur milieu.
$\centerdot\ \ $ L'isobarycentre de trois points non alignés est le centre de gravité du triangle.
I.2 Produit scalaire
Considérons les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$. Soient les vecteurs $\vec{u}$ et $\vec{v}$ tels que :
$\overrightarrow{AB}=\vec{u}$ et $\overrightarrow{AC}=\vec{v}$
On a :
$\begin{array}{rdl}\vec{u}\cdot\vec{v}&=&||\vec{u}||\times||\vec{v}||\times cos(\vec{u}\;,\ \vec{v})\\ \\&=&\overline{AB}\times\overline{AH}\\ \\&=&xx'+yy'\end{array}$
où $H$ est le projeté orthogonal de $C$ sur $(AB)$ et $\vec{u}$ et $\vec{v}$ de coordonnées respectives $(x\;,\ y)$ et $(x'\;,\ y')$ dans le repère orthonormé.
I.2.1 Propriétés
$\centerdot\ \ \vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$
$\centerdot\ \ \vec{u}\cdot(\alpha\vec{v})=(\alpha\vec{u}\cdot\vec{v})=\alpha(\vec{u}\cdot\vec{v})$
$\centerdot\ \ \vec{u}\cdot(\vec{v}+\vec{w})=\vec{v}\cdot\vec{u}=\vec{u}\cdot\vec{v}+\vec{u}\cdot\vec{w}$
$\centerdot\ \ \vec{u}\neq\vec{0}\;, \quad \vec{v}\neq\vec{0}\;, \quad \vec{u}\cdot\vec{v}=0\ \Leftrightarrow\ \vec{u}\perp\vec{v}$
I.2.2 Relation d'Alkashi
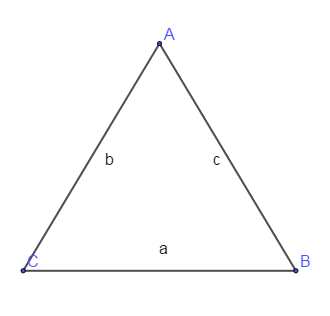
Soit $ABC$ un triangle d'angles $\widehat{A}\;,\ \widehat{B}$ et $\widehat{C}$ respectivement opposés aux cotés $a$, $\ b$ et $c$. Nous avons :
$a^{2}=b^{2}+c^{2}-2bc.cos\widehat{A}$
$b^{2}=a^{2}+c^{2}-2ac.cos\widehat{B}$
$c^{2}=a^{2}+b^{2}-2ab.cos\widehat{C}$
$\dfrac{sin\widehat{A}}{a}=\dfrac{sin\widehat{B}}{b}=\dfrac{sin\widehat{C}}{c}=\dfrac{2\mathcal{S}}{abc}$ où $\mathcal{S}$ est la surface du triangle $(ABC)$
I.2.3 Théorème de la médiane
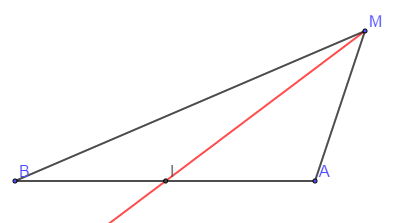
Soient $I$ milieu du segment $[AB]$ et $M$ un point du plan tel que $MBA$ soit un triangle. Alors on a :
$$\begin{array}{rcl}\overrightarrow{MI}&=&\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MB}\right)\\ \\MA^{2}+MB^{2}&=&2MI^{2}+\dfrac{AB^{2}}{2}\end{array}$$
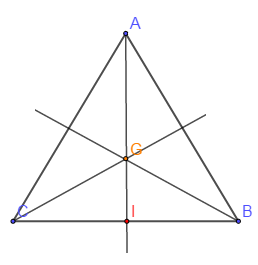
Soit $ABC$ un triangle, $G$ son centre de gravité et $I$ milieu du segment $[BC]$;
$\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}$
$\overrightarrow{IG}=\dfrac{1}{3}\overrightarrow{IA}$
II Fonctions vectorielles de leibniz
II.1 Définitions
Soient $(A_{i})_{1\leq i\leq n}$ des points de $\mathbf{E}\;,\ (\alpha_{i})_{1\leq i\leq n}\in\mathbb{R}$. On appelle fonction vectorielle de Leibniz l'application $\vec{f}$ définie dans $\vec{E}$ (l'ensemble des vecteurs) par :
$$\forall\;M\in\mathbf{E} \quad \overrightarrow{f(M)}=\sum_{i=1}^{n} \alpha_{i}\overrightarrow{MA}_{i}=\alpha_{1}\overrightarrow{MA}_{1}+\alpha_{2}\overrightarrow{MA}_{2}+\ldots+\alpha_{n}\overrightarrow{MA}_{n}$$
$\centerdot\ \ $ Remarque : si $G$ est barycentre de $(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$ alors $\overrightarrow{f(G)}=\vec{0}$
II.2 Expression réduite de $\overrightarrow{f(M)}$
$\textbf{1er cas :}$
si $\sum\alpha_{i}=0$
$\begin{array}{rcl}\overrightarrow{f(M)}&=&\alpha_{1}\overrightarrow{MA}_{1}+\alpha_{2}\overrightarrow{MA}_{2}+\ldots+\alpha_{n}\overrightarrow{MA}_{n}\\ \\ &=&\alpha_{1}\left(\overrightarrow{MO}+\overrightarrow{OA}_{1}\right)+\alpha_{2}\left(\overrightarrow{MO}+\overrightarrow{OA}_{2}\right)+\ldots+\alpha_{n}\left(\overrightarrow{MO}+\overrightarrow{OA}_{n}\right)\\ \\ &=&\alpha_{1}\overrightarrow{MO}+\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{MO}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{MO}+\alpha_{n}\overrightarrow{OA}_{n}\\ \\ &=&(\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n})\overrightarrow{MO}+\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}\\ \\ &=&\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}\\ \\ &=&\overrightarrow{f(O)}\end{array}$
Donc, $\overrightarrow{f}$ est constante.
$\textbf{2ème cas :}$
si $\sum\alpha_{i}\neq 0$, alors $(A_{i}\;,\ \alpha_{i})_{1\leq i\leq n}$ admettent un barycentre; soit $G$ ce barycentre.On a
$$\overrightarrow{f(M)}=\sum_{i=1}^{n} \alpha_{i}\overrightarrow{MA}_{i}=\left(\sum_{i=1}^{n} \alpha_{i}\right)\overrightarrow{MG}$$
III Fonctions scalaires de Leibniz
III.1 Définitions
Soient $(A_{i})_{1\leq i\leq n}$ $n$ points, $(\alpha_{i})_{1\leq i\leq n}\in\mathbb{R}.$ On appelle fonction scalaire de Leibniz l'application définie de $\mathbf{E}$ vers $\mathbb{R}$ par :
$$f(M)=\sum_{i=1}^{n} \alpha_{i}MA^{2}_{i}$$
III.2 Expression réduite de $f(M)$
$\textbf{1er cas :}$
si $\sum\alpha_{i}=0$,
$\begin{array}{rcl} f(M)&=&\alpha_{1}\overrightarrow{MA_{1}}^{2}+\alpha_{2}\overrightarrow{MA_{2}}^{2}+\ldots+\alpha_{n}\overrightarrow{MA_{n}}^{2}\\ \\&=& \alpha_{1}\left(\overrightarrow{MO}+\overrightarrow{OA_{1}}\right)^{2}+\alpha_{2}\left(\overrightarrow{MO}+\overrightarrow{OA_{2}}\right)^{2}+\ldots+\alpha_{n}\left(\overrightarrow{MO}+\overrightarrow{OA_{n}}\right)^{2}\\ \\&= &(\alpha_{1}+\alpha_{2}+\ldots+\alpha_{n})\overrightarrow{MO}^{2}+\alpha_{1}\overrightarrow{OA_{1}}^{2}+\alpha_{2}\overrightarrow{OA_{2}}^{2}+\ldots+\alpha_{n}\overrightarrow{OA_{n}}^{2}\\ \\&& +\;2\overrightarrow{MO}\cdot\left(\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}\right)\\ \\&=& f(O)+2\overrightarrow{MO}\cdot\left(\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}\right)\end{array}$
Donc, $$f(M)=f(O)+2\overrightarrow{MO}\cdot\left(\alpha_{1}\overrightarrow{OA}_{1}+\alpha_{2}\overrightarrow{OA}_{2}+\ldots+\alpha_{n}\overrightarrow{OA}_{n}\right)$$
$\textbf{2ème cas :}$
si $\sum\alpha_{i}\neq 0$, alors $(A_{i},\ \alpha_{i})_{1\leq i\leq n}$ admettent un barycentre; soit $G$ ce barycentre.On a :
$\begin{array}{rcl} f(M)&=&\alpha_{1}\left(\overrightarrow{MG}+\overrightarrow{GA_{1}}\right)^{2}+\alpha_{2}\left(\overrightarrow{MG}+\overrightarrow{GA_{2}}\right)^{2}+\ldots+\alpha_{n}\left(\overrightarrow{MG}+\overrightarrow{GA_{n}}\right)^{2}\\ \\&=&\left(\sum_{i=1}^{n} \alpha_{i}\right)\overrightarrow{MG}^{2}+f(G)+2\overrightarrow{MG}\cdot\left(\alpha_{1}\overrightarrow{GA}_{1}+\alpha_{2}\overrightarrow{GA}_{2}+\ldots+\alpha_{n}\overrightarrow{GA}_{n}\right) \end{array}$
Ainsi $$f(M)=\left(\sum_{i=1}^{n} \alpha_{i}\right)\overrightarrow{MG}^{2}+f(G)$$
Exercice d'application
Soit $ABC$ un triangle tel que $AB=AC=5$ et $BC=6$.
1) Calculer $\overrightarrow{AB}\cdot\overrightarrow{AC}$
2) Soit $G$ barycentre de $(A\;,\ 2)\;,\ (B\;,\ 3)$ et $(C\;,\ 3)$
a) Calculer $AG$
b) Soit $f(M)$ une fonction scalaire de Leibniz définie par $$f(M)=2\overrightarrow{MB}\cdot\overrightarrow{MC}+\overrightarrow{MA}\cdot(\overrightarrow{MC}+\overrightarrow{MB})$$
Montrer que $f(M)=4MG^{2}+f(G)$
c) Calculer $f(A)$ et $f(G)$
d) Déterminer l'ensemble des points $M$ tels que $f(M)=f(A)$.
Résolution
1) $\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\times AC\times\cos\widehat{A}=bc\cos\widehat{A}$, or d'après Alkashi on a :
$a^{2}=b^{2}+c^{2}-2bc.cos\widehat{A}\ \Rightarrow\ \cos\widehat{A}=\dfrac{b^{2}+c^{2}-a^{2}}{2bc}$ et donc
$\begin{array}{rcl} \overrightarrow{AB}\cdot\overrightarrow{AC}&=&bc\dfrac{b^{2}+c^{2}-a^{2}}{2bc}\\ \\&=&\dfrac{b^{2}+c^{2}-a^{2}}{2}\\ \\&=&\dfrac{25+25-36}{2}\\ \\&=&7\end{array}$
2) a) $G$ barycentre de $(A\;,\ 2)\;,\ (B\;,\ 3)$ et $(C\;,\ 3)$, alors
$\begin{array}{rcl}\overrightarrow{AG}&=&\dfrac{3\overrightarrow{AB}+3\overrightarrow{AC}}{8}\\ \\ \Rightarrow\ AG^{2}&=&\dfrac{9}{64}(AB^{2}+AC^{2}+2\overrightarrow{AB}\cdot\overrightarrow{AC})\\ \\&=&\dfrac{9}{64}(25+25+2\times 7)\\ \\&=&9\end{array}$
Donc, $AG=3$
b)
$\begin{array}{rcl} f(M)&=&2\overrightarrow{MB}\cdot\overrightarrow{MC}+\overrightarrow{MA}\cdot(\overrightarrow{MC}+\overrightarrow{MB})\\ \\ &=&2(\overrightarrow{MG}+\overrightarrow{GB})\cdot(\overrightarrow{MG}+\overrightarrow{GC})+(\overrightarrow{MG}+\overrightarrow{GA})\cdot((\overrightarrow{MG}+\overrightarrow{GC})+(\overrightarrow{MG}+\overrightarrow{GB}))\\ \\ &=&4MG^{2}+\overrightarrow{MG}\cdot\underbrace{(2\overrightarrow{MA}+3\overrightarrow{MB}+3\overrightarrow{MC})}_{\vec{0}}+2\overrightarrow{GB}\cdot\overrightarrow{GC}+\overrightarrow{GA}\cdot(\overrightarrow{GC}+\overrightarrow{GB})\\ \\ &=&4MG^{2}+2\overrightarrow{GB}\cdot\overrightarrow{GC}+\overrightarrow{GA}\cdot(\overrightarrow{GC}+\overrightarrow{GB})\\ \\ &=&4MG^{2}+f(G)\end{array}$
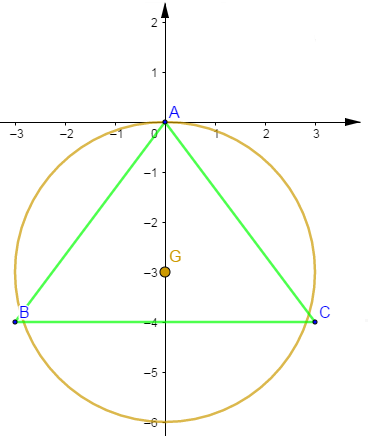
c) $f(A)=2\overrightarrow{AB}\cdot\overrightarrow{AC}=14$
On a : $f(M)=4MG^{2}+f(G)$, alors $f(G)=f(M)-4MG^{2}$ et donc pour $M=A$ on trouve
$$f(G)=f(A)-4AG^{2}=-22$$
d)
$\begin{array}{rcl} f(M)=f(A)&\Leftrightarrow&4MG^{2}+f(G)=f(A)\\ \\ &\Leftrightarrow&4MG^{2}=f(A)-f(G)\\ \\ &\Leftrightarrow&MG^{2}=\dfrac{f(A)-f(G)}{4}\\ \\ &\Leftrightarrow&MG=\sqrt{\dfrac{14+22}{4}}\ =\ 3\end{array}$
Donc, l'ensemble des points $M$ tels que $f(M)=f(A)$ est le cercle de centre $G$ et de rayon 3.
IV Surfaces et lignes de niveau
- $E=\left\lbrace M/ \ \vec{u}\cdot\overrightarrow{MA}=k\right\rbrace$ , $\ \vec{u}$ est un vecteur donné, $A$ un point de $E$ et $k\in\mathbb{R}$.
$\centerdot\ \ $ Dans le plan $E$ est une droite perpendiculaire à la direction de $\vec{u}$.
$\centerdot\ \ $ Dans l'espace $E$ est un plan perpendiculaire à la direction de $\vec{u}$
- $E=\left\lbrace M/ \ MA=MB\right\rbrace$
$\centerdot\ \ $ Dans le plan $E$ est la médiatrice de $[AB]$.
$\centerdot\ \ $ Dans l'espace $E$ est le plan médiateur du segment $[AB]$
- $E=\left\lbrace M/ \ AM=k>0\right\rbrace$
$\centerdot\ \ $ Dans le plan $E=\mathcal{C}(A,\ k)$, le cercle de centre $A$ et de rayon $k$.
$\centerdot\ \ $ Dans l'espace $E=\mathcal{S}(A,\ k)$, la sphère de centre $A$ et de rayon $k$
- $E=\left\lbrace M/ \ \overrightarrow{MA}\cdot\overrightarrow{MB}=0\right\rbrace$
$\centerdot\ \ $ Dans le plan $E$ est le cercle de diamètre $[AB]$
$\centerdot\ \ $ Dans l'espace $E$ est la sphère de diamètre $[AB]$
Auteur:
Seyni Ndiaye & Diny Faye

Commentaires
agnideachabi (non vérifié)
ven, 08/03/2018 - 17:30
Permalien
Calcul vectoriel
vianney (non vérifié)
dim, 11/14/2021 - 13:53
Permalien
La notion est bien détaillé j
Anonyme (non vérifié)
sam, 09/24/2022 - 23:26
Permalien
Z
Ajouter un commentaire