Angles - Trigonométrie - 1er S
Classe:
Première
I Angles non orientés
I.1 Définition
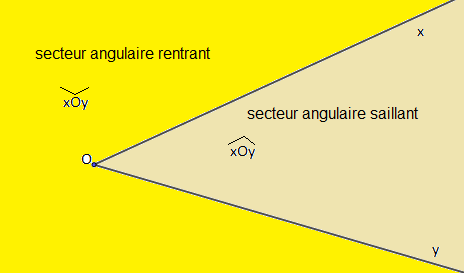
Deux demi-droites de même origine $O$ divise le plan en deux parties appelées secteurs angulaires. On a le secteur angulaire saillant noté $\widehat{xOy}$ et le secteur angulaire rentrant noté $\overset{\displaystyle\vee}{xOy}$
Les unités de mesure sont : le radian $(rd)$ ; le degré $(^{\circ})$ ; le grade $(gr).$
Nous avons les correspondances suivantes :
\begin{eqnarray} 180^{\circ} &\rightarrow & \pi\;rd\;\rightarrow\;200\;gr \nonumber \\ 30^{\circ} &\rightarrow & \dfrac{\pi}{6}\;rd\;\rightarrow\;\dfrac{200}{6}=\dfrac{100}{3}\;gr \nonumber \\ 45^{\circ} &\rightarrow & \dfrac{\pi}{4}\;rd\;\rightarrow\;50\;gr \nonumber \\ 60^{\circ} &\rightarrow & \dfrac{\pi}{3}\;rd\;\rightarrow\;\dfrac{200}{3}\;gr \nonumber \\ 90^{\circ} &\rightarrow & \dfrac{\pi}{2}\;rd\;\rightarrow\;100\;gr \nonumber \end{eqnarray}
I.2 Angles alternes internes, alternes externes, correspondants, opposés par le sommet
Soient deux droites $(\Delta)$ et $(\Delta')$ parallèles et $(D)$ une droite sécante à $(\Delta)$ et à $(\Delta')$ respectivement en $A$ et $B.$
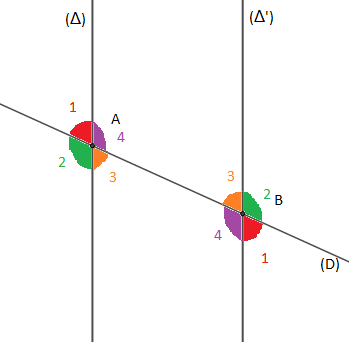
$\centerdot\ \ \left\lbrace\begin{array}{lll} \widehat{A}_{3}\;\text{ et }\;\widehat{B}_{3}\\ \widehat{A}_{4}\;\text{ et }\;\widehat{B}_{4} \end{array}\right.\;\ \text{ sont alternes internes donc }\; \widehat{A}_{3}=\widehat{B}_{3}\;\text{ et }\;\widehat{A}_{4}=\widehat{B}_{4}$
$\centerdot\ \ \left\lbrace\begin{array}{lll} \widehat{A}_{1}\;\text{ et }\;\widehat{B}_{1}\\ \widehat{A}_{2}\;\text{ et }\;\widehat{B}_{2} \end{array}\right.\;\ \text{ sont alternes externes donc }\; \widehat{A}_{1}=\widehat{B}_{1}\;\text{ et }\;\widehat{A}_{2}=\widehat{B}_{2}$
$\centerdot\ \ \left\lbrace\begin{array}{lll} \widehat{A}_{1}\;\text{ et }\;\widehat{B}_{3}\\ \widehat{A}_{4}\;\text{ et }\;\widehat{B}_{2}\\ \widehat{A}_{3}\;\text{ et }\;\widehat{B}_{1}\\ \widehat{A}_{2}\;\text{ et }\;\widehat{B}_{4} \end{array}\right.\;\ \text{ sont des angles correspondants donc }$
$\widehat{A}_{1}=\widehat{B}_{3}\;,\ \widehat{A}_{4}=\widehat{B}_{2}\;,\ \widehat{A}_{3}=\widehat{B}_{1}\;\text{ et }\;\widehat{A}_{2}=\widehat{B}_{4}$
$\centerdot\ \ \left\lbrace\begin{array}{lll} \widehat{A}_{1}\;\text{ et }\;\widehat{A}_{3}\\ \widehat{A}_{4}\;\text{ et }\;\widehat{A}_{2}\\ \widehat{B}_{3}\;\text{ et }\;\widehat{B}_{1}\\ \widehat{B}_{2}\;\text{ et }\;\widehat{B}_{4} \end{array}\right.\;\ \text{ sont des angles opposés par le sommet donc }$
$mes\;\widehat{A}_{1}=mes\;\widehat{A}_{3}\;,\ mes\;\widehat{A}_{4}=mes\;\widehat{A}_{2}\;,\ mes\;\widehat{B}_{3}=mes\;\widehat{B}_{1}\;\text{ et }\;mes\;\widehat{B}_{2}=mes\;\widehat{B}_{4}$
I.3 Angle au centre - Angle inscrit
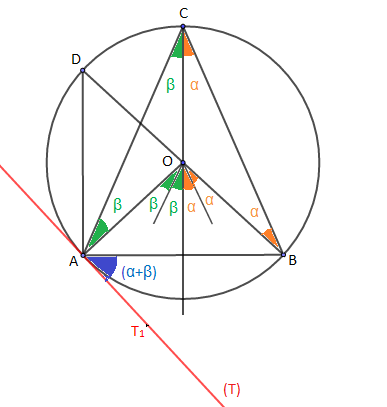
$A\;,\ B\;,\ C\;,\ D\;\in\;\mathcal{C}(O\;,\ R)$
$(T)$ est la tangente à $(\mathcal{C})$ en $A$
l'angle $\widehat{AOB}$ est un angle au centre qui intercepte l'arc $\overset{\displaystyle\frown}{AB}$
$\widehat{ADB}$ et $\widehat{ACB}$ sont des angles inscrits qui interceptent l'arc $\overset{\displaystyle\frown}{AB}$
$\left(\widehat{(AT_{1})\;,\ (AB)}\right)$ est l'angle formé par la tangente en $A$ et la droite $(AB)$
Soit $\widehat{ACB}=\alpha+\beta$
On a :
$\begin{array}{rcl} \widehat{AOB} &=& \beta+\beta+\alpha+\alpha \\ \\ &=& 2\beta+2\alpha \\ \\ &=& 2(\beta+\alpha) \\ \\ \Rightarrow\;\;\widehat{AOB} &=& 2\widehat{ACB}\end{array}$
$\centerdot\ \ $ L'angle au centre est le double de l'angle inscrit s'ils interceptent le même arc.
$\centerdot\ \ $ Deux angles inscrits qui interceptent le même arc sont égaux.
$$\left(\widehat{(AT_{1})\;,\ (AB)}\right)=\widehat{ACB}=\dfrac{1}{2}\widehat{AOB}$$
$\centerdot\ \ $ Points cocycliques : on dira que quatre points $A\;,\ B\;,\ C\;,\ D$ sont cocycliques (appartiennent à un même cercle) ou alignés si, et seulement si,
$$\begin{array}{rcl} \widehat{ABC} &=& \widehat{ADC} \\ \\ \widehat{CAB} &=& \widehat{CDB} \\ \\ \widehat{ABD} &=& \widehat{ACD} \end{array}$$
I.4 Longueur de l'arc
Soit $\mathcal{C}(O\;,\ R)$ de centre $O$ et de rayon $R$ ; $A$ et $B$ deux points de $(\mathcal{C})$ tels que $\widehat{AOB}=\theta.$
$\centerdot\ \ $ La longueur de l'arc $\overset{\displaystyle\frown}{AB}$ est donnée par $$\ell_{\overset{\displaystyle\frown}{AB}}=R\times\theta$$
On a :
$$\begin{array}{rcl} 2\pi &\rightarrow & 2\pi R \\ \\ \theta &\rightarrow & \dfrac{2\pi R\times\theta}{2\pi}=R\times\theta\end{array}$$
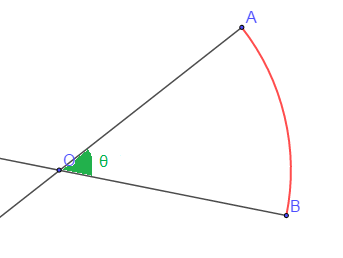
$\centerdot\ \ $ L'aire du secteur angulaire $\mathcal{S}$ est donnée par
$$\mathcal{S}=\dfrac{\theta\times R^{2}}{2}$$
On a :
$$\begin{array}{rcl} 2\pi & \rightarrow & \pi R^{2} \\ \\ \theta & \rightarrow & \dfrac{\pi R^{2}\times\theta}{2\pi}=\dfrac{\theta\times R^{2}}{2}\end{array}$$
II Angles orientés
II.1 Orientation du plan
On a deux sens de parcours d'un cercle.
Le sens contraire des aiguilles d'une montre est appelé sens positif et le sens des aiguilles d'une montre est appelé sens négatif.
Orienté le plan, c'est choisir comme sens positif le sens contraire des aiguilles d'une montre.
II.2 Angles orientés de demi-droites, de vecteurs
II.2.1 Définition
Soient $[Ox)$ et $[Oy)$ deux demi-droites de même origine $O.$
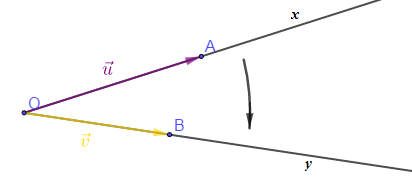
L'angle orienté de demi-droites $[Ox)$ et $[Oy)$ noté $\left(\displaystyle\widehat{[Ox)\;,\ [Oy)}\right)$ est l'angle qui a pour sommet $O$ et pour extrémités $[Ox)$ et $[Oy)$, orienté de $[Ox)$ vers $[Oy).$
Si $\vec{u}$ est un vecteur directeur de $[Ox)$ tel que $\vec{u}=\overrightarrow{OA}$ avec $A\in[Ox)$ et $\vec{v}$ un vecteur directeur de $[Oy)$ tel que $\vec{v}=\overrightarrow{OB}$ avec $B\in[Oy)$ alors l'angle orienté de vecteurs $\vec{u}$ et $\vec{v}$ noté $(\vec{u}\;,\ \vec{v})$ est égal à l'angle orienté de demi-droites $\left(\widehat{[Ox)\;,\ [Oy)}\right)$ qui est orienté de $[Ox)$ vers $[Oy).$
On a $$(\vec{u}, \vec{v})=\left(\widehat{[Ox)\;,\ [Oy)}\right)$$
II.2.2 Propriétés
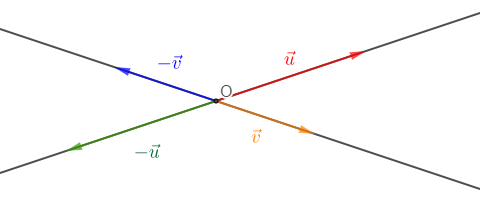
$\centerdot\ \ (\vec{u}\;,\ \vec{v})=-(\vec{v}\;,\ \vec{u})\;[2\pi]$
$\centerdot\ \ (-\vec{u}\;,\ \vec{v})=(\vec{u}\;,\ -\vec{v})=\pi+(\vec{u}\;,\ \vec{v})$
$\centerdot$ $(-\vec{u}\;,\ -\vec{v})=(\vec{u}\;,\ \vec{v})\;[2\pi]$
$\centerdot\ \ (k\vec{u}\;,\ k\vec{v})=(\vec{u}\;,\ \vec{v})\;[2\pi] \quad \forall\;k\neq 0$
$\centerdot\ \ (k\vec{u}\;,\ \vec{v})=\left\lbrace\begin{array}{ll} (\vec{u}\;,\ \vec{v})\;[2\pi] & \text{ si }k>0\\ \pi+(\vec{u}\;,\ \vec{v})\;[2\pi] & \text{ si }k<0 \end{array}\right.$
$\centerdot\ \ (\vec{u}\;,\ \vec{v})+(\vec{v}\;,\ \vec{w})=(\vec{u}\;,\ \vec{w})\;[2\pi]$ (Relation de Chasles)
$\centerdot\ \ \vec{u}_{1}\perp\vec{u}_{2}\;$ et $\;\vec{v}_{1}\perp\vec{v}_{2}\;$ alors $\;(\vec{u}_{1}\;,\ \vec{v}_{1})=(\vec{u}_{2}\;,\ \vec{v}_{2})\;[\pi]$
II.3 Lignes de niveau
Définition
Soient $A$ et $B$ deux points du plan $\mathcal{P}$ et soit l'application \begin{eqnarray} f\ :\ \mathcal{P}&\rightarrow&\mathbb{R} \nonumber \\ M&\rightarrow&f(M)=(\overrightarrow{MA}\;,\ \overrightarrow{MB}) \nonumber \end{eqnarray}
Soit $\theta\in\mathbb{R}$ ; la ligne de niveau $\theta$ est l'ensemble des points $M$ du plan $\mathcal{P}$ tels que $f(M)=\theta$
Exemples
a) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=0\;[\pi]\right\rbrace$ est la droite $(AB)$ privée des points $A$ et $B.$
b) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=0\;[2\pi]\right\rbrace$ est la droite $(AB)$ privée des points du segment $[AB].$
c) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=\pi\;[2\pi]\right\rbrace$ est le segment $[AB]$ privé des points $A$ et $B.$
d) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=\pi\;[\pi]\right\rbrace$ est la droite $(AB).$
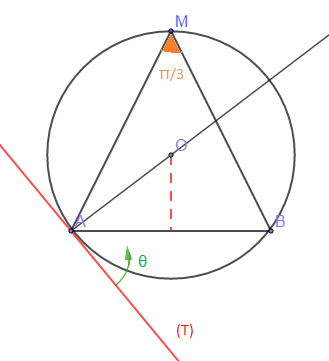
e) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=\theta\;[\pi]\right\rbrace$ est un cercle passant par $A$ et $B$ et privé de des points $A$ et $B.$
f) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=\theta\;[2\pi]\right\rbrace$ est un arc de cercle.
g) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=\dfrac{\pi}{2}\;[\pi]\right\rbrace$ est le cercle de diamètre $[AB]$ privé des points $A$ et $B.$
h) l'ensemble $\mathbf{E}=\left\lbrace M\in\mathcal{P}\;;\ (\overrightarrow{MA}\;,\ \overrightarrow{MB})=\dfrac{\pi}{2}\;[2\pi]\right\rbrace$ est un demi-cercle.
III Trigonométrie
III.1 Cercle trigonométrique et angles remarquables
III.1.1 Définition
On appelle cercle trigonométrique le cercle de centre $O$ et de rayon 1, orienté.
III.1.2 Angles associés
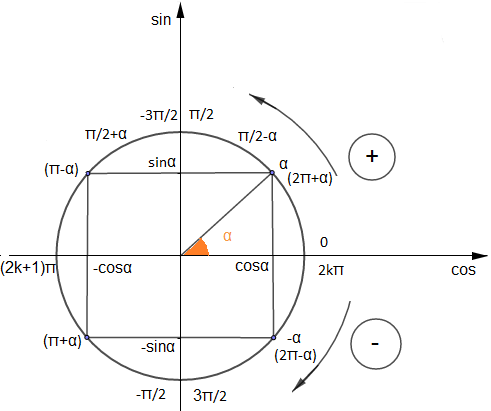
Dans la liste qui suit, nous allons donner quelques relations en fonctions de $\cos\alpha$ et $\sin\alpha.$
On a :
$\cos(\alpha+2k\pi)=\cos\alpha\;,\qquad\sin(\alpha+2k\pi)=\sin\alpha$
$\cos(-\alpha)=\cos\alpha\;,\qquad\sin(-\alpha)=-\sin\alpha$ $\cos(\pi-\alpha)=-\cos\alpha\;,\qquad\sin(\pi-\alpha)=\sin\alpha$
$\cos(\pi+\alpha)=-\cos\alpha\;,\qquad\sin(\pi+\alpha)=-\sin\alpha$
$\cos\left(\dfrac{\pi}{2}-\alpha\right)=\sin\alpha\;,\qquad\sin\left(\dfrac{\pi}{2}-\alpha\right)=\cos\alpha$
$\cos\left(\dfrac{\pi}{2}+\alpha\right)=-\sin\alpha\;,\qquad\sin\left(\dfrac{\pi}{2}+\alpha\right)=\cos\alpha$
$\tan(\pi-\alpha)=-\tan\alpha\;,\qquad\tan(\pi+\alpha)=\tan\alpha$
$\tan(\alpha+2k\pi)=\tan\alpha\;,\qquad\tan(-\alpha)=-\tan\alpha$
Le tableau ci-après nous donne le cosinus et le sinus des angles remarquables
$$\begin{array}{|c|c|c|c|c|c|} \hline & & & & & \\ \alpha & 0 & \dfrac{\pi}{6} & \dfrac{\pi}{4} & \dfrac{\pi}{3} & \dfrac{\pi}{2} \\ & & & & & \\ \hline & & & & & \\ \sin\alpha & 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1 \\ & & & & & \\ \hline & & & & & \\ \cos\alpha & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \\ & & & & & \\ \hline & & & & & \\ \tan\alpha & 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & \times \\ & & & & & \\ \hline \end{array}$$
Exemple :
Déterminer les cosinus et sinus de : $\dfrac{77\pi}{4}\;,\ \dfrac{81\pi}{6}\;,\ -\dfrac{17\pi}{3}$
Résolution :
Soit $\alpha\;;\ -\pi<\alpha\leq\pi$ et $k\in\mathbb{Z}$
a) posons $\dfrac{77\pi}{4}=\alpha+2k\pi\;\Rightarrow\;\alpha=\dfrac{77\pi}{4}-2k\pi$ alors on a
$$\begin{array}{rcccl} -\pi&<& \dfrac{77\pi}{4}-2k\pi&\leq&\pi \\ \\ -\pi-\dfrac{77\pi}{4}&<&-2k\pi&\leq&\pi-\dfrac{77\pi}{4} \\ \\ \dfrac{77\pi}{4}-\pi&\leq&2k\pi&<&\dfrac{77\pi}{4}+\pi\\ \\ 18.25&\leq&2k&<&20.25\\ \\ 9.125&\leq&k&<&10.125 \end{array}$$
On obtient : $k=10\;\Rightarrow\;\alpha=-\dfrac{3\pi}{4}$
Donc,
$\begin{array}{rcl} \cos\dfrac{77\pi}{4}&=&\cos\left(-\dfrac{3\pi}{4}\right)\\ \\&=&\cos\dfrac{3\pi}{4}\\ \\&=&\cos\left(\pi-\dfrac{\pi}{4}\right)\\ \\&=&-\cos\dfrac{\pi}{4}\\ \\&=&-\dfrac{\sqrt{2}}{2}\end{array}$
De même,
$\begin{array}{rcl} \sin\dfrac{77\pi}{4}&=&\sin\left(\pi-\dfrac{\pi}{4}\right)\\ \\&=&\sin\dfrac{\pi}{4}\\ \\&=& \dfrac{\sqrt{2}}{2}\end{array}$
D'où, $$\cos\dfrac{77\pi}{4}=-\dfrac{\sqrt{2}}{2}\quad\text{ et }\quad\sin\dfrac{77\pi}{4}=\dfrac{\sqrt{2}}{2}$$
b) posons $\dfrac{81\pi}{6}=\alpha+2k\pi\;\Rightarrow\;\alpha=\dfrac{81\pi}{6}-2k\pi$ alors on a
$$\begin{array}{rcccl} -\pi&<&\dfrac{81\pi}{6}-2k\pi&\leq &\pi\\ \\-\pi-\dfrac{81\pi}{6}&<&-2k\pi&\leq &\pi-\dfrac{81\pi}{6}\\ \\ \dfrac{81\pi}{6}-\pi&\leq&2k\pi&<&\dfrac{81\pi}{6}+\pi\\ \\12.5&\leq&2k&<&14.5\\ \\6.25&\leq&k&<&7.25 \end{array}$$
On obtient : $k=7\;\Rightarrow\;\alpha=-\dfrac{3\pi}{4}$
Donc, $$\cos\dfrac{81\pi}{6}=-\dfrac{\sqrt{2}}{2}\quad\text{ et }\quad\sin\dfrac{81\pi}{6}=\dfrac{\sqrt{2}}{2}$$
c) On a : $-\dfrac{17\pi}{3}=-\dfrac{18\pi}{3}+\dfrac{\pi}{3}=-6\pi+\dfrac{\pi}{3}$
Donc, $\cos\left(-\dfrac{17\pi}{3}\right)=\cos\dfrac{\pi}{3}=\dfrac{1}{2}\quad\text{et}\quad\sin\left(-\dfrac{17\pi}{3}\right)=\sin\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}$
III.1.3 Coordonnées polaires
Soit $\mathcal{P}$ un plan muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ et $M\begin{pmatrix} x\\ y\end{pmatrix}$ un point de $\mathcal{P}.$
$x$ et $y$ sont les coordonnées de $M$ dans le repère $(O\;;\ \vec{i}\;,\ \vec{j}).$
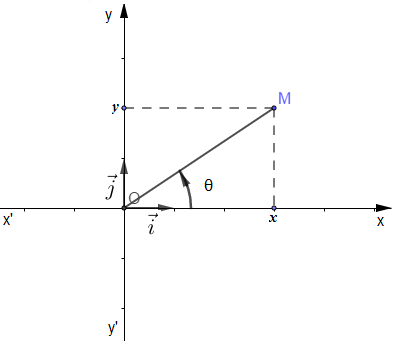
On pose $OM=||\overrightarrow{OM}||=r\;$ et $\;(\vec{i}\;,\ \overrightarrow{OM})=\theta.$
$r\;$ et $\;\theta$ sont appelés coordonnées polaires de $M.$
On a alors $\left\lbrace\begin{array}{lcr} x &=& r\cos\theta\\ y &=& r\sin\theta \end{array}\right.$
III.2 Formules d'addition et de multiplication par deux
III.2.1 Formules d'addition
Soient $A$ et $B$ deux point appartenant à $\mathcal{C}(O\;,\ 1)$ tels que $\;(\vec{i}\;,\ \overrightarrow{OA})=a$ et $\;(\vec{i}\;,\ \overrightarrow{OB})=b.$
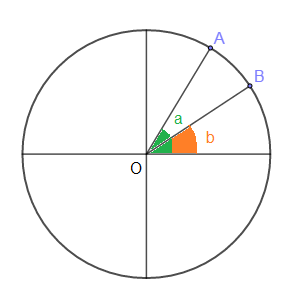
$1^{e}\;$ façon
Soit $OA=||\overrightarrow{OA}||=1\;$ et $\;OB=||\overrightarrow{OB}||=1$
On a : $\overrightarrow{OA}\begin{pmatrix} OA\cos a\\ OA\sin a \end{pmatrix}\;$ et $\;\overrightarrow{OB}\begin{pmatrix} OB\cos b\\ OB\sin b \end{pmatrix}$
Alors, $\overrightarrow{OA}\cdot\overrightarrow{OB}=\cos a\cos b+\sin a\sin b$
$2^{e}\;$ façon
Soit $(\overrightarrow{OA}\;,\ \overrightarrow{OB})=(a-b)$
On a : $\overrightarrow{OA}\cdot\overrightarrow{OB}=||\overrightarrow{OA}||.||\overrightarrow{OB}||.\cos(\overrightarrow{OA}\;,\ \overrightarrow{OB})=\cos(a-b)$
en combinant les deux méthodes on obtient :
$$\boxed{\cos(a-b)=\cos a\cos b+\sin a\sin b}$$
Par conséquent, on a :
$\cos(a+b)=\cos(a-(-b))=\cos a\cos(-b)+\sin a\sin(-b)$
Or, $\cos(-b)=\cos b\;$ et $\;\sin(-b)=-\sin b$
Donc, $$\boxed{\cos(a+b)=\cos a\cos b-\sin a\sin b}$$
$\begin{array}{rcl}\sin(a+b) &=& \cos\left[\dfrac{\pi}{2}-(a+b)\right] \\ \\ &=& \cos\left[\left(\dfrac{\pi}{2}-a\right)-b)\right] \\ \\ &=& \sin a\cos b+\cos a\sin b\end{array}$
D'où, $$\boxed{\sin(a+b)=\sin a\cos b+\cos a\sin b}$$
Par suite,
$\sin(a-b)=\sin(a+(-b))=\sin a\cos(-b)+\cos a\sin(-b)$
D'où, $$\boxed{\sin(a-b)=\sin a\cos b-\cos a\sin b}$$
En résumé on a :
\begin{eqnarray} \cos(a-b) &=& \cos a\cos b+\sin a\sin b\quad (1) \\ \cos(a+b) &=& \cos a\cos b-\sin a\sin b\quad (2) \\ \sin(a+b) &=& \sin a\cos b+\cos a\sin b\quad (3) \\ \sin(a-b) &=& \sin a\cos b-\cos a\sin b\quad (4) \end{eqnarray}
En conséquence, nous obtenons les relations suivantes :
$\begin{array}{rcl} \tan(a+b) &=& \dfrac{\sin(a+b)}{\cos(a+b)} \\ \\ &=& \dfrac{\sin a\cos b+\cos a\sin b}{\cos a\cos b-\sin a\sin b}\\ \\&=&\dfrac{\dfrac{\sin a\cos b+\cos a\sin b}{\cos a\cos b}}{\dfrac{\cos a\cos b-\sin a\sin b}{\cos a\cos b}} \\ \\ &=& \dfrac{\dfrac{\sin a\cos b}{\cos a\cos b}+\dfrac{\cos a\sin b}{\cos a\cos b}}{\dfrac{\cos a\cos b}{\cos a\cos b}-\dfrac{\sin a\sin b}{\cos a\cos b}} \\ \\ & & \nonumber \\ &=& \dfrac{\tan a+\tan b}{1-\tan a\tan b} \end{array}$
D'où, $$\boxed{\tan(a+b)=\dfrac{\tan a+\tan b}{1-\tan a\tan b}}$$
et par suite
$\tan(a-b)=\tan(a+(-b))=\dfrac{\tan a+\tan(-b)}{1-\tan a\tan(-b)}$
Or, $\tan(-b)=-\tan b$
donc, $$\boxed{\tan(a-b)=\dfrac{\tan a-\tan b}{1+\tan a\tan b}}$$
Exemple :
Donner les valeurs exactes de :
$\cos\dfrac{\pi}{12}\;,\ \sin\dfrac{\pi}{12}\;,\ \cos\dfrac{7\pi}{12}\;,\ \sin\dfrac{7\pi}{12}$
Résolution :
$\begin{array}{rcl} \cos\dfrac{\pi}{12} &=& \cos\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right) \\ \\ &=& \cos\dfrac{\pi}{3}\cos\dfrac{\pi}{4}+\sin\dfrac{\pi}{3}\sin\dfrac{\pi}{4} \\ \\ &=& \dfrac{1}{2}\times\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{3}}{2}\times\dfrac{\sqrt{2}}{2} \\ \\ &=& \dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4} \end{array}$
D'où, $$\boxed{\cos\dfrac{\pi}{12}=\dfrac{\sqrt{2}+\sqrt{6}}{4}}$$
$\begin{array}{rcl} \sin\dfrac{\pi}{12} &=& \sin\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right) \\ \\ &=& \sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}-\cos\dfrac{\pi}{3}\sin\dfrac{\pi}{4} \\ \\ &=& \dfrac{\sqrt{3}}{2}\times\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\times\dfrac{\sqrt{2}}{2} \\ \\ &=& \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4} \end{array}$
D'où, $$\boxed{\sin\dfrac{\pi}{12}=\dfrac{\sqrt{6}-\sqrt{2}}{4}}$$
$\begin{array}{rcl} \cos\dfrac{7\pi}{12} &=& \cos\left(\dfrac{\pi}{3}+\dfrac{\pi}{4}\right) \\ \\ &=& \cos\dfrac{\pi}{3}\cos\dfrac{\pi}{4}-\sin\dfrac{\pi}{3}\sin\dfrac{\pi}{4} \\ \\ &=& \dfrac{1}{2}\times\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{3}}{2}\times\dfrac{\sqrt{2}}{2} \\ \\ &=& \dfrac{\sqrt{2}}{4}-\dfrac{\sqrt{6}}{4} \end{array}$
D'où, $$\boxed{\cos\dfrac{7\pi}{12}=\dfrac{\sqrt{2}-\sqrt{6}}{4}}$$
$\begin{array}{rcl} \sin\dfrac{7\pi}{12} &=& \sin\left(\dfrac{\pi}{3}+\dfrac{\pi}{4}\right) \\ \\ &=& \sin\dfrac{\pi}{3}\cos\dfrac{\pi}{4}+\cos\dfrac{\pi}{3}\sin\dfrac{\pi}{4} \\ \\ &=& \dfrac{\sqrt{3}}{2}\times\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\times\dfrac{\sqrt{2}}{2} \\ \\ &=& \dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4} \end{array}$
D'où, $$\boxed{\sin\dfrac{7\pi}{12}=\dfrac{\sqrt{6}+\sqrt{2}}{4}}$$
$\centerdot\ \ $ Autres formes
En additionnant les relations (1) et (2) du résumé on obtient
$$(1)+(2)\;\Rightarrow\;2\cos a\cos b=\cos(a+b)+\cos(a-b)$$
Donc, $$\boxed{\cos a\cos b=\dfrac{\cos(a+b)+\cos(a-b)}{2}}$$
Et leur différence donne :
$(1)-(2)\;\Rightarrow\;2\sin a\sin b=\cos(a-b)-\cos(a+b)$
Ainsi, $$\boxed{\sin a\sin b=\dfrac{\cos(a-b)-\cos(a+b)}{2}}$$
Enfin en additionnant les relations (3) et (4) on a
$(3)+(4)\;\Rightarrow\;2\sin a\cos b=\sin(a+b)+\sin(a-b)$
D'où, $$\boxed{\sin a\cos b=\dfrac{\sin(a+b)+\sin(a-b)}{2}}$$
Remarque
En posant $\left\lbrace\begin{array}{lcr} a+b&=&p\\ a-b&=&q\end{array}\right.\ \Rightarrow\ \left\lbrace\begin{array}{lcr} a&=&\dfrac{p+q}{2}\\ \\ b&=&\dfrac{p-q}{2}\end{array}\right.$ on obtient les relations suivantes :
$$\boxed{\cos p+\cos q=2\cos\dfrac{p+q}{2}\cos\dfrac{p-q}{2}}\qquad\boxed{\cos p-\cos q=-2\sin\dfrac{p+q}{2}\sin\dfrac{p-q}{2}}$$
$$\boxed{\sin p+\sin q=2\sin\dfrac{p+q}{2}\cos\dfrac{p-q}{2}}\qquad\boxed{\sin p-\sin q=2\sin\dfrac{p-q}{2}\cos\dfrac{p+q}{2}}$$
$$\boxed{\tan p+\tan q=\dfrac{\sin(p+q)}{\cos p\cos q}}\qquad\boxed{\tan p-\tan q=\dfrac{\sin(p-q)}{\cos p\cos q}}$$
III.2.2 Formules de multiplication par deux
Soit les relations suivantes :
\begin{eqnarray} \cos(a+b) &=& \cos a\cos b-\sin a\sin b\quad (5) \\ \sin(a+b) &=& \sin a\cos b+\cos a\sin b\quad (6) \\ \tan(a+b) &=& \dfrac{\tan a+\tan b}{1-\tan a\tan b} \qquad\quad\quad (7) \end{eqnarray}
Dans la relation (5) remplaçons $b$ par $a$, alors on obtient
$\cos 2a=\cos a\cos a-\sin a\sin a=\cos^{2}a-\sin^{2}a$
Donc $$\boxed{\cos 2a=\cos^{2}a-\sin^{2}a}$$
mais comme $\cos^{2}a+\sin^{2}a=1$ alors,
$\cos 2a=\cos^{2}a-(-\cos^{2}a+1)=2\cos^{2}a-1$
Ainsi, $$\boxed{\cos 2a=2\cos^{2}a-1}$$
Aussi, $\cos 2a=\cos^{2}a-\sin^{2}a=1-\sin^{2}a-\sin^{2}a$
Ce qui donne : $$\boxed{\cos 2a=1-2\sin^{2}a}$$
Par analogie on a :
\begin{eqnarray} \cos x &=& \cos^{2}\dfrac{x}{2}-\sin^{2}\dfrac{x}{2} \nonumber \\ \cos x &=& 2\cos^{2}\dfrac{x}{2}-1 \nonumber \\ \cos x &=& 1-2\sin^{2}\dfrac{x}{2} \nonumber \end{eqnarray}
En remplaçant $b$ par $a$, dans la relation (6), on obtient
$$\boxed{\sin 2a=2\sin a\cos a}$$
De même, en prenant $b=a$ dans la relation (7), on obtient
$$\boxed{\tan 2a=\dfrac{2\tan a}{1-\tan^{2} a}}$$
En conséquence, nous avons :
$\begin{array}{rcl} \cos t &=& \cos^{2}\dfrac{t}{2}-\sin^{2}\dfrac{t}{2} \\ \\ &=& \dfrac{\cos^{2}\dfrac{t}{2}-\sin^{2}\dfrac{t}{2}}{1} \\ \\ &=& \dfrac{\cos^{2}\dfrac{t}{2}-\sin^{2}\dfrac{t}{2}}{\cos^{2}\dfrac{t}{2}+\sin^{2}\dfrac{t}{2}}\\ \\&=&\dfrac{\dfrac{\cos^{2}\dfrac{t}{2}}{\cos^{2}\dfrac{t}{2}}-\dfrac{\sin^{2}\dfrac{t}{2}}{\cos^{2}\dfrac{t}{2}}}{\dfrac{\cos^{2}\dfrac{t}{2}}{\cos^{2}\dfrac{t}{2}}+\dfrac{\sin^{2}\dfrac{t}{2}}{\cos^{2}\dfrac{t}{2}}} \\ \\ &=& \dfrac{1-\tan^{2}\dfrac{t}{2}}{1+\tan^{2}\dfrac{t}{2}} \end{array}$
Ainsi, $$\boxed{\cos t=\dfrac{1-\tan^{2}\dfrac{t}{2}}{1+\tan^{2}\dfrac{t}{2}}}$$
De même,
$\begin{array}{rcl} \sin t &=& 2\sin\dfrac{t}{2}\cos\dfrac{t}{2} \\ \\ &=& \dfrac{2\sin\dfrac{t}{2}\cos\dfrac{t}{2}}{\cos^{2}\dfrac{t}{2}+\sin^{2}\dfrac{t}{2}} \\ \\ &=& \dfrac{2\tan\dfrac{t}{2}}{1+\tan^{2}\dfrac{t}{2}} \end{array}$
Donc, $$\boxed{\sin t=\dfrac{2\tan\dfrac{t}{2}}{1+\tan^{2}\dfrac{t}{2}}}$$
Exercice d'application
Factoriser $1-\cos x+\sin x$
Résolution
On a :
$\begin{array}{rcl} 1-\cos x+\sin x&=&\cos^{2}\dfrac{x}{2}+\sin^{2}\dfrac{x}{2}-\cos^{2}\dfrac{x}{2}+\sin^{2}\dfrac{x}{2}+2\sin\dfrac{x}{2}\cos\dfrac{x}{2} \\ \\ &=&2\sin^{2}\dfrac{x}{2}+2\sin\dfrac{x}{2}\cos\dfrac{x}{2} \\ \\ &=&2\sin\dfrac{x}{2}\left(\sin\dfrac{x}{2}+\cos\dfrac{x}{2}\right) \\ \\ &=&2\sin\dfrac{x}{2}\left(\sin\dfrac{x}{2}+\sin\left(\dfrac{\pi}{2}-\dfrac{x}{2}\right)\right) \\ \\ &=&2\sin\dfrac{x}{2}\left(2\sin\dfrac{\pi}{4}\cos\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)\right) \\ \\ &=&2\sin\dfrac{x}{2}\left(\sqrt{2}\cos\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right)\right) \\ \\ &=&2\sqrt{2}\sin\dfrac{x}{2}\cos\left(\dfrac{x}{2}-\dfrac{\pi}{4}\right) \end{array}$
III.3 Équations et Inéquations trigonométriques
III.3.1 Équations trigonométriques
III.3.1.1 Équations du type $\cos x=a$
Si $a\notin[-1\;;\ 1]$ l'équation n'admet pas de solution ; $S=\emptyset$
Si $a\in[-1\;;\ 1]$ alors il existe un seul réel $\alpha\in[0\;;\ \pi]$ tel que $a=\cos\alpha$
L'équation devient : $\cos x=\cos\alpha$
Deux angles ayant même cosinus sont égaux ou opposés $$\cos x=\cos\alpha\ \Leftrightarrow\ \left\lbrace\begin{array}{lcr} x&=&\alpha+2k\pi \\ &\text{ou}& \\ x&=&-\alpha+2k'\pi\end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z}$$
$$S=\{\alpha+2k\pi\;;\ -\alpha+2k'\pi\;,\quad (k\;;\ k')\in\mathbb{Z}^{2}\}$$
Exemple
Résoudre dans $\mathbb{R}\ \cos x=\dfrac{1}{2}$
$\begin{array}{rcl} \cos x=\dfrac{1}{2}&\Leftrightarrow&\cos x=\cos\dfrac{\pi}{3} \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcr} x&=&\dfrac{\pi}{3}+2k\pi \\ &\text{ou}& \\ x&=&-\dfrac{\pi}{3}+2k'\pi\end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z} \end{array}$
$$S=\left\{\dfrac{\pi}{3}+2k\pi\;;\ -\dfrac{\pi}{3}+2k'\pi\;,\quad (k\;;\ k')\in\mathbb{Z}^{2}\right\}$$
III.3.1.2 Équations du type $\sin x=a$
Si $a\notin[-1\;;\ 1]$ l'équation n'admet pas de solution ; $S=\emptyset$
Si $a\in[-1\;;\ 1]$ alors il existe un seul réel $\alpha\in\left[-\dfrac{\pi}{2}\;;\ \dfrac{\pi}{2}\right]$ tel que $a=\cos\alpha$
L'équation devient $\cos x=\cos\alpha$
Deux angles ayant même sinus sont égaux ou supplémentaires $$\sin x=\sin\alpha\ \Leftrightarrow\ \left\lbrace\begin{array}{lcr} x&=&\alpha+2k\pi \\ &\text{ou}& \\ x&=&\pi-\alpha+2k'\pi\end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z}$$
$$S=\{\alpha+2k\pi\;;\ \pi-\alpha+2k'\pi\;,\quad (k\;;\ k')\in\mathbb{Z}^{2}\}$$
Exemple
Résoudre dans $\mathbb{R}\ \sin x=\dfrac{\sqrt{2}}{2}$
$\begin{array}{rcl} \sin x=\dfrac{\sqrt{2}}{2}&\Leftrightarrow&\sin x=\cos\dfrac{\pi}{4} \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcr} x&=&\dfrac{\pi}{4}+2k\pi \\ &\text{ou}& \\ x&=&\pi-\dfrac{\pi}{4}+2k'\pi\end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z} \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcr} x&=&\dfrac{\pi}{4}+2k\pi \\ &\text{ou}& \\ x&=&\dfrac{3\pi}{4}+2k'\pi\end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z} \end{array}$
$$S=\left\{\dfrac{\pi}{4}+2k\pi\;;\ \dfrac{3\pi}{4}+2k'\pi\;,\quad (k\;;\ k')\in\mathbb{Z}^{2}\right\}$$
III.3.1.3 Équations du type $\tan x=a$
Pour tout réel $a$, il existe un seul réel $\alpha\in\;\left]-\dfrac{\pi}{2}\;;\ \dfrac{\pi}{2}\right[$ tel que $\tan x=\tan\alpha$
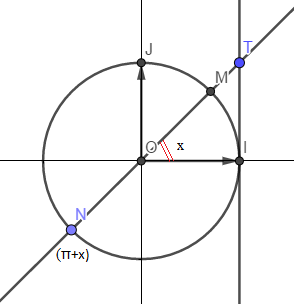
Dire que $\tan x=\tan\alpha$ revient à dire que les droites $(OM)$ et $(ON)$ coupent l'axe des tangentes au même point. Donc :
$-$ Soit $M=N$ ce qui signifie que $x=\alpha+2k\pi$
$-$ Soit $M$ et $N$ sont symétriques par rapport à $O$ et alors : $x=\alpha+\pi+2k'\pi$
Remarque :
Dans le dernier cas, on peut écrire : $x=\alpha+(2k'+1)\pi$, donc dans tous les cas on : $x=\alpha+k\pi\;;\ k\in\mathbb{Z}$
$$S=\{\alpha+k\pi\;;\quad k\in\mathbb{Z}\}$$
Exemple
Résoudre dans $\mathbb{R}\ \tan x=1$
$\begin{array}{rcl} \tan x=1&\Leftrightarrow&\tan x=\tan\dfrac{\pi}{4} \\ \\ &\Leftrightarrow&x=\dfrac{\pi}{4}+k\pi\;;\quad k\in\mathbb{Z} \end{array}$
$$S=\left\{\dfrac{\pi}{4}+k\pi\;;\quad k\in\mathbb{Z}\right\}$$
III.3.1.4 Équations du type $a\cos x+b\sin x=c$
Transformons d'abord $a\cos x+b\sin x$ en $A\cos(x+\theta)$ ou en $A\sin(x+\varphi)$
On a : $$a\cos x+b\sin x=\sqrt{a^{2}+b^{2}}\left(\dfrac{a}{\sqrt{a^{2}+b^{2}}}\cos x+\dfrac{b}{\sqrt{a^{2}+b^{2}}}\sin x\right)$$
De plus $\left(\dfrac{a}{\sqrt{a^{2}+b^{2}}}\right)^{2}+\left(\dfrac{b}{\sqrt{a^{2}+b^{2}}}\right)^{2}=1$ or $\forall\;\alpha\in\mathbb{R}\;;\ \cos^{2}\alpha+\sin^{2}\alpha=1$
Donc soit $\left\lbrace\begin{array}{lcr} \cos\alpha&=&\dfrac{a}{\sqrt{a^{2}+b^{2}}} \\ \\ \sin\alpha&=&\dfrac{b}{\sqrt{a^{2}+b^{2}}} \end{array}\right.\quad\text{ou}\quad\left\lbrace\begin{array}{lcr} \sin\alpha&=&\dfrac{a}{\sqrt{a^{2}+b^{2}}} \\ \\ \cos\alpha&=&\dfrac{b}{\sqrt{a^{2}+b^{2}}} \end{array}\right.$
D'où,
$\begin{array}{rcl} a\cos x+b\sin x&=&\sqrt{a^{2}+b^{2}}(\cos\alpha\cos x+\sin\alpha\sin x) \\ \\ &=&\sqrt{a^{2}+b^{2}}\cos(x-\alpha) \end{array}$
ou encore
$\begin{array}{rcl} a\cos x+b\sin x&=&\sqrt{a^{2}+b^{2}}(\sin\alpha\cos x+\cos\alpha\sin x) \\ \\ &=&\sqrt{a^{2}+b^{2}}\sin(x+\alpha) \end{array}$
Exemple
Résoudre dans $\mathbb{R}\ \cos x+\sqrt{3}\sin x=\sqrt{3}$
$a=1\;;\ b=\sqrt{3}$ donc $\sqrt{a^{2}+b^{2}}=\sqrt{4}=2$
Ainsi,
$\begin{array}{rcl} \cos x+\sqrt{3}\sin x&=&2\left(\dfrac{1}{2}\cos x+\dfrac{\sqrt{3}}{2}\sin x\right) \\ \\ &=&2\left(\cos\dfrac{\pi}{3}\cos x+\sin\dfrac{\pi}{3}\sin x\right) \\ \\ &=&2\cos\left(x-\dfrac{\pi}{3}\right) \end{array}$
$\begin{array}{rcl} \cos x+\sqrt{3}\sin x=\sqrt{3}&\Leftrightarrow&2\cos\left(x-\dfrac{\pi}{3}\right)=\sqrt{3} \\ \\ &\Leftrightarrow&\cos\left(x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2} \\ \\ &\Leftrightarrow&\cos\left(x-\dfrac{\pi}{3}\right)=\cos\dfrac{\pi}{6} \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcr} x-\dfrac{\pi}{3}&=&\dfrac{\pi}{6}+2k\pi \\ &\text{ou}& \\ x-\dfrac{\pi}{3}&=&-\dfrac{\pi}{6}+2k'\pi\end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z} \\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{lcr} x&=&\dfrac{\pi}{2}+2k\pi \\ &\text{ou}& \\ x-\dfrac{\pi}{3}&=&\dfrac{\pi}{6}+2k'\pi \end{array}\right.\;;\quad k\;,\ k'\in\mathbb{Z} \end{array}$
$$S=\left\{\dfrac{\pi}{2}+2k\pi\;;\ \dfrac{\pi}{6}+2k'\pi\;,\quad (k\;;\ k')\in\mathbb{Z}^{2}\right\}$$
III.3.2 Inéquations trigonométriques
Les inéquations trigonométriques de la forme $\cos x\geq a\;,\ \sin x\geq a$ ou $\tan x\geq a$ se résolvent par lecture graphique sur un cercle trigonométrique.
Les solutions d'une inéquation trigonométriques sont généralement une réunion d'intervalles, dont les bornes sont les solutions de l'équation correspondante.
Exemple 1
Soit à résoudre, dans l'intervalle $[0\;;\ 2\pi]$ l'inéquation : $$\sin x >-\dfrac{1}{2}$$
On commence par chercher une valeur simple pour laquelle $\sin x=-\dfrac{1}{2}.$ Ici on prendra $x=-\dfrac{\pi}{6}.$
On trace un cercle trigonométrique pour retrouver les autres valeurs sur la parallèle à l'axe des abscisses passant par le point correspondant à $-\dfrac{\pi}{6}.$
Attention on travaille dans l'intervalle $[0\;;\ 2\pi]$, les valeurs retenues seront donc $\dfrac{7\pi}{6}$ et $\dfrac{11\pi}{6}.$
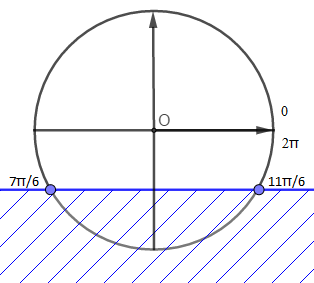
D'après la figure ci-dessus, les valeurs pour lesquelles $\sin x >-\dfrac{1}{2}$ sont les valeurs situées au dessus de la droite horizontale en bleu.
On conclut que : $$S=\left[0\;;\ \dfrac{7\pi}{6}\right[\cup\left]\dfrac{11\pi}{6}\;;\ 2\pi\right]$$
Exemple 2
Soit à résoudre, dans l'intervalle $]-\pi\;;\ \pi]$ l'inéquation : $$2\cos x-1<0$$
Elle est équivalente à $\cos x<\dfrac{1}{2}.$ On commence par chercher une valeur simple pour laquelle $\cos x=\dfrac{1}{2}.$ Ici on prendra $x=\dfrac{\pi}{3}.$
On trace un cercle trigonométrique pour retrouver les autres valeurs sur la parallèle à l'axe des ordonnées passant par le point correspondant à $\dfrac{\pi}{3}.$
Attention on travaille sur l'intervalle $]-\pi\;;\ \pi]$, les valeurs retenues seront donc $-\dfrac{\pi}{3}$ et $\dfrac{\pi}{3}.$
Les points $M$ d'abscisse $x$ pour lesquels $\cos x<\dfrac{1}{2}$ sont les points situés à gauche de la droite verticale en bleu sur le schéma ci-dessous.
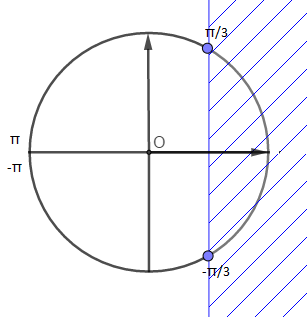
On conclut que : $$S=\left]-\pi\;;\ -\dfrac{\pi}{3}\right[\cup\left]\dfrac{\pi}{3}\;;\ \pi\right]$$
Exemple 3
Soit à résoudre, dans l'intervalle $[0\;;\ 2\pi[$ l'inéquation : $$\tan x>1$$
Elle est équivalente à $\tan x>\tan\dfrac{\pi}{4}.$ D'après l'interprétation géométrique de la tangente, pour que le réel $x$ soit solution, il faut que le point $M$ d'abscisse $x$ soit situé sur l'un des arcs de cercle en rouge de la figure ci-dessous :
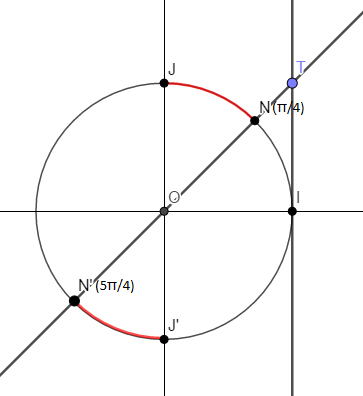
On en conclut que : $$S=\left]\dfrac{\pi}{4}\;;\ \dfrac{\pi}{2}\right[\cup\left]\dfrac{5\pi}{4}\;;\ \dfrac{3\pi}{2}\right[$$
Auteur:
Diny Faye & Seyni Ndiaye

Commentaires
Anonyme (non vérifié)
sam, 11/09/2019 - 10:53
Permalien
Très bien fait ;complet.
Ajouter un commentaire