Calcul dans R - 2nd
Classe:
Seconde
I. Ensemble de nombres
Activité
1) Remplir le tableau suivant en mettant des croix si l'élément appartient à l'ensemble.
$$\begin{array}{|c|c|c|c|c|c|}
\hline
& \mathbb{N} & \mathbb{Z} & \mathbb{D} & \mathbb{Q} & \mathbb{R} \\
\hline
0 & & & & & \\
\hline
-2 & & & & & \\
\hline
1.4 & & & & & \\
\hline
0.4 & & & & & \\
\hline
\pi & & & & & \\
\hline
\frac{1}{3} & & & & & \\
\hline
\frac{3}{5} & & & & & \\
\hline
\sqrt{3} & & & & & \\
\hline
\end{array}$$
\hline
& \mathbb{N} & \mathbb{Z} & \mathbb{D} & \mathbb{Q} & \mathbb{R} \\
\hline
0 & & & & & \\
\hline
-2 & & & & & \\
\hline
1.4 & & & & & \\
\hline
0.4 & & & & & \\
\hline
\pi & & & & & \\
\hline
\frac{1}{3} & & & & & \\
\hline
\frac{3}{5} & & & & & \\
\hline
\sqrt{3} & & & & & \\
\hline
\end{array}$$
2) Répondre par vrai ou faux
$\dfrac{5}{4}\in\mathbb{D}\;,\ -2\in\mathbb{Q}\;,\ 6.13\in\mathbb{D}\;,\ \sqrt{7}\in\mathbb{Q}$
$\mathbb{Z}\subset\mathbb{Q}\;,\ \mathbb{Q}\subset\mathbb{D}\;,\ \mathbb{N}\subset\mathbb{D}$
I.1 Définition
Soient les ensembles de nombres suivants :
$\mathbb{N}$ : ensembles des entiers naturels
$\mathbb{Z}$ : ensembles des entiers relatifs
$\mathbb{D}$ : ensembles des nombres décimaux
$\mathbb{Q}$ : ensembles des nombres rationnels
$\mathbb{R}$ : ensembles des nombres réels
I.2 Propriété
Nous avons : $\mathbb{N}\subset\mathbb{Z}\subset\mathbb{D}\subset\mathbb{Q}\subset\mathbb{R}$
II. Puissance
II.1 Définition
On appelle puissance $n^{ième}$ d'un nombre $a$, le nombre noté $a^{n}$ et qui est défini par :
$\centerdot\ \ n=0\qquad\qquad a^{0}=1$
$\centerdot\ \ n=1\qquad\qquad a^{1}=a$
$\centerdot\ \ $ si $n>0\ $ alors, $\ a^{n}=\underbrace{a\times a \ldots\times a}_{n\ \mathrm{fois}}$
$\centerdot\ \ $ si $n<0\ $ alors, $\ a^{n}=\dfrac{1}{\underbrace{a\times a \ldots\times a}_{n\ \mathrm{fois}}}$
$\centerdot\ \ -a^{n}=-(\underbrace{a\times a \ldots\times a}_{n\ \mathrm{fois}})$ ; l'exposant $n$ concerne le $a$
$\centerdot\ \ (-a)^{n}=\underbrace{(-a)\times (-a) \ldots\times (-a)}_{n\ \mathrm{fois}}$
$\centerdot\ \ (-a)^{n}=a^{n}\ $ si $n$ est pair
$\centerdot\ \ (-a)^{n}=-a^{n}\ $ si $n$ est impair
II.2 Propriétés
Soient $a,\ b\in\mathbb{R}$ et $n$ un entier relatif. Nous avons :
$\centerdot\ \ (ab)^{n}=a^{n}\times(b)^{n}$
$\centerdot\ \ a^{n}\times a^{m}=a^{n+m}$
$\centerdot\ \ (a^{n})^{m}=a^{n\times m}$
$\centerdot\ \ a^{n}=\dfrac{1}{a^{-n}}\ ;\qquad a^{-n}=\dfrac{1}{a^{n}}$
$\centerdot\ \ \dfrac{a^{n}}{a^{m}}=a^{n-m}$
$\centerdot\ \ b\not=0;\ \left(\dfrac{a}{b}\right)^{n}=\dfrac{a^{n}}{b^{n}}$
Exercice d'application
Écrire les réels suivants sous la forme de produits de puissance de nombres premiers
$$A=32\;,\quad B=-54^{4}\;,\quad C=\dfrac{0.16\times 2700000}{50}\;,\quad D=\dfrac{81^{3}\times 64^{2}}{36^{5}}\;,\quad E=\left(2^{3}\right)^{5}\times\left(\dfrac{3}{5}\right)^{3}\times 25\times 7^{3}$$
$$A=32\;,\quad B=-54^{4}\;,\quad C=\dfrac{0.16\times 2700000}{50}\;,\quad D=\dfrac{81^{3}\times 64^{2}}{36^{5}}\;,\quad E=\left(2^{3}\right)^{5}\times\left(\dfrac{3}{5}\right)^{3}\times 25\times 7^{3}$$
Résolution
$\begin{array}{rcl} A &=& 32\\ \\&=& 2\times 2\times 2\times 2\times 2\\ \\&=& 2^{5}\end{array}$
$\begin{array}{rcl} B &=& -54^{4} \\ \\&=& -\left(2\times 3^{3}\right)^{4}\\ \\&=& -2^{4}\times 3^{12}\end{array}$
$\begin{array}{rcl} C&=&\dfrac{0.16\times 2700000}{50}\\ \\&=&\dfrac{4^{2}\times 10^{-2}\times 3^{3}\times 10^{5}}{5\times 10^{1}} \\ \\&=& \left(2^{2}\right)^{2}\times 3^{3}\times 10^{-2}\times 10^{5}\times 10^{-1}\times 5^{-1} \\ \\ &=& 2^{4}\times 3^{3}\times 10^{2}\times 5^{-1} \\ \\ &=& 2^{4}\times 3^{3}\times 2^{2}\times 5^{2}\times 5^{-1} \\ \\ &=& 2^{6}\times 3^{3}\times 5^{1} \end{array}$
$\begin{array}{rcl} D&=&\dfrac{81^{3}\times 64^{2}}{36^{5}}\\ \\&=&\dfrac{\left(9^{2}\right)^{3}\times \left(2^{6}\right)^{2}}{\left(6^{2}\right)^{5}} \\ \\ &=& \dfrac{9^{6}\times 2^{12}}{6^{10}} \\ \\ &=& \dfrac{\left(3^{2}\right)^{6}\times 2^{12}}{2^{10}\times 3^{10}} \\ \\ &=& \dfrac{3^{12}\times 2^{12}}{2^{10}\times 3^{10}} \\ \\ &=& 3^{12}\times 2^{12}\times 2^{-10}\times 3^{-10} \\ \\ &=& 3^{2}\times 2^{2}\end{array}$
$\begin{array}{rcl} E &=& \left(2^{3}\right)^{5}\times\left(\dfrac{3}{5}\right)^{3}\times 25\times 7^{3} \\ \\ &=& 2^{3\times 5}\times\dfrac{3^{3}}{5^{3}}\times 5^{2}\times 7^{3} \\ \\ &=& 2^{15}\times 3^{3}\times 5^{-1}\times 7^{3} \end{array}$
II.3 Égalités remarquables
$\forall\;a,\ b\in\mathbb{R}$, nous avons les expressions suivantes appelées égalités remarquables :
$\centerdot\ \ (a+b)^{2}=a^{2}+2ab+b^{2}$
$\centerdot\ \ (a-b)^{2}=a^{2}-2ab+b^{2}$
$\centerdot\ \ (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
$\centerdot\ \ (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}$
$\centerdot\ \ a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$
$\centerdot\ \ a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$
Exercice d'application
a) Développer les expressions suivantes
$A=\left(2x^{2}-4y\right)^{2}$
$B=\left(2x^{2}y-3z\right)^{3}$
b) Factoriser
$C=\left(4a^{2}+b^{2}-9\right)^{2}-16a^{2}b^{2}$
Résolution
a) Développons
$\begin{array}{rcl} A &=& \left(2x^{2}-4y\right)^{2}\\ \\&=& \left(2x^{2}\right)^{2}-2\left(2x^{2}\right)\left(4y\right)+(4y)^{2}\\ \\&=& 4x^{4}-16x^{2}y+16y^{2}\end{array}$
$\begin{array}{rcl} B &=& \left(2x^{2}y-3z\right)^{3}\\ \\&=& \left(2x^{2}y\right)^{3}-3\left(2x^{2}y\right)^{2}(3z)+3(2x^{2}y)(3z)^{2}-(3z)^{3}\\ \\&=& 8x^{6}y^{3}-36x^{4}y^{2}z+54x^{2}yz^{2}-9z^{3}\end{array}$
b) Factorisons
$\begin{array}{rcl} C &=& \left(4a^{2}+b^{2}-9\right)^{2}-16a^{2}b^{2}\\ \\&=& \left(4a^{2}+b^{2}-9-4ab\right)\left(4a^{2}+b^{2}-9+4ab\right)\\ \\&=& \left[\left(4a^{2}-4ab+b^{2}\right)-9\right]\left[\left(4a^{2}+4ab+b^{2}\right)-9\right] \\ \\&=& \left[(2a-b)^{2}-9\right]\left[(2a+b)^{2}-9\right]\\ \\&=& (2a-b-3)(2a-b+3)(2a+b-3)(2a+b+3)\end{array}$
III. Racines carrés
Activité
1) Écrire les nombres suivants sans radicaux au dénominateur
$\dfrac{2}{\sqrt{3}-3}$; $\quad \dfrac{7}{\sqrt{6}-\sqrt{2}}$; $\quad \dfrac{3}{\sqrt{6}}$
2) On donne $a=\sqrt{9-4\sqrt{5}}+\sqrt{9+4\sqrt{5}}$; $\quad b=\sqrt{7-4\sqrt{3}}-\sqrt{7+4\sqrt{3}}$
Calculer $a^{2}$ et $b^{2}$. En déduire une expression simplifiée de $a$ et $b$.
3) Déterminer $a$, $\ b$ et $c$ pour que
$\sqrt{7+\sqrt{a}}=3$; $\quad\sqrt{b+\sqrt{36}}=7$; $\quad\sqrt{77}+\sqrt{11+\sqrt{25}}=c$
4) Résoudre $x^{2}=3-2\sqrt{2}$; $\quad x^{2}=-9$
5) Montrer que $a>0$, $\quad b>0$, $\quad a>b$
$\left(\sqrt{a+\sqrt{a^{2}-b^{2}}}+\sqrt{a-\sqrt{a^{2}-b^{2}}}\right)^{2}=2(a+b)$
III.1 Définition
On appelle racine carrée d'un nombre réel positif $a$ le réel noté $\sqrt{a}$ dont le carré est égal à $a$.
III.2 Propriétés
$\centerdot\ \ (\sqrt{a})^{2}=a$
$\centerdot\ \ \sqrt{a^{2}}=|a|$
$\centerdot\ \ a\geq 0\ ,\ b\geq 0\ ;\qquad \sqrt{ab}=\sqrt{a}\times\sqrt{b}$
$\centerdot\ \ a\geq 0\ ,\ b>0\ ;\qquad \sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{a}}{\sqrt{b}}$
$\centerdot\ \ x^{2}=a\ $ avec $a$ positif $\Rightarrow\ x=\sqrt{a}\ $ ou $x=-\sqrt{a}$
Attention : $\sqrt{a+b}\neq\sqrt{a}+\sqrt{b};\qquad$ $\forall a>0,\ b>0$
IV. Valeur absolue
Activité
1) Écrire sans le symbole de la valeur absolue
$|\sqrt{5}-2|\,$; $\quad|\sqrt{3}-2|\,$; $\quad|1+\sqrt{3}2\sqrt{2}|$
2) Déterminer $x$ pour que $|x|=3\,$; $\quad|x|=-2\,$; $\quad|x|<4\,$; $\quad|x|>7\,$; $\quad|x|=0\,$; $\quad|x|<-2\,$
IV.1 Définition
On appelle valeur absolue d'un nombre réel $a$, le réel noté $$|a|=\left\lbrace\begin{array}{ll}
a & \text{si }a\geq 0\\
-a & \text{si }a\leq 0
\end{array}
\right.$$
a & \text{si }a\geq 0\\
-a & \text{si }a\leq 0
\end{array}
\right.$$
IV.2 Propriétés
Soient $a,\ b,\ k\in\mathbb{R}$, $x$ un nombre quelconque. On a :
$\centerdot\ \ k>0$
$\cdot\ \ |x|=k\ \Leftrightarrow\ x=k\ \mbox{ ou }\ x=-k\ \Leftrightarrow\ x\in\{k;\ -k\}$
$\cdot\ \ |x|\leq k\ \Leftrightarrow\ -k\leq x\leq k\ \Leftrightarrow\ x\in[-k;\ k]$
$\cdot\ \ |x|\geq k\ \Leftrightarrow\ x\geq k\ \mbox{ou}\ x\leq -k\ \Leftrightarrow\ x\in]-\infty;\ -k]\cup[k;\ +\infty[$
$\centerdot\ \ k<0$
$\cdot\ \ |x|=k\;;\ \mbox{ impossible }\ S=\emptyset$
$\cdot\ \ |x|\leq k\;;\ \mbox{ impossible }\ S=\emptyset$
$\centerdot\ \ |a|=|b|\ \Leftrightarrow\ a=b\ \mbox{ ou }\ a=-b$
$\centerdot\ \ |ab|=|a|\cdot|b|$
$\centerdot\ \ b\not=0\;;\ \ \left|\dfrac{a}{b}\right|=\dfrac{|a|}{|b|}$
$\centerdot\ \ |a^{n}|=|a|^{n}$
$\centerdot\ \ |a^{2}|=|a|^{2}=a^{2}$
$\centerdot\ \ \sqrt{x^{2}}=|x|$
$\centerdot\ \ |a+b|\leq|a|+|b|$
Exercice d'application
1) Dans chacun des cas suivants, écrire les fonctions sans le symbole de la valeur absolue
a) $f(x)=|2x-3|$
b) $g(x)=|x-2|-3|x+5|$
2) Résoudre dans $\mathbb{R}$
a) $f(x)=1$
b) $g(x)=-2x+7$
c) $1\leq f(x)\leq 4$
d) $\left|\dfrac{x+3}{x}\right|>-1$
Résolution
1) a) $f(x)=|2x-3|$
On a : $2x-3=0\ \Leftrightarrow\ x=\dfrac{3}{2}$
Soit le tableau de signes suivant :
$$\begin{array}{|c|lcccr|} \hline x&-\infty& &3/2& &+\infty \\ \hline 2x-3& &-&|&+& \\ \hline |2x-3|& &-2x+3&|&2x-3& \\ \hline\end{array}$$
Donc on obtient :
$$f(x)=\left\lbrace\begin{array}{rcccc} -2x+3&\text{si}&x&\leq&\dfrac{3}{2} \\ \\ 2x-3&\text{si}&x&\geq&\dfrac{3}{2} \end{array}\right.$$
b) $g(x)=|x-2|-3|x+5|$
On a : $x-2=0\ \Leftrightarrow\ x=2\quad\text{et}\quad x+5=0\ \Leftrightarrow\ x=-5$
Tableau de signes
$$\begin{array}{|c|lcccccr|} \hline x&-\infty& &-5& &2& &+\infty \\ \hline x-2& &-&|&-&|&+& \\ \hline |x-2|& &-x+2&|&-x+2&|&x-2& \\ \hline x+5& &-&|&+&|&+& \\ \hline |x+5|& &-x-5&|&x+5&|&x+5& \\ \hline\end{array}$$
Donc,
sur $]-\infty\;,\ -5]\;,\quad g(x)=-x+2-3x-15=-4x-13$
sur $[-5\;,\ 2]\;,\quad g(x)=-x+2+3x+15=2x+17$
sur $[2\;,\ +\infty[\;,\quad g(x)=x-2+3x+15=4x+13$
2) a)
$\begin{array}{rcl} f(x)=1 &\Leftrightarrow& |2x-3|=1\\ \\ &\Leftrightarrow& 2x-3=1\ \text{ ou }\ 2x-3=-1\\ \\ &\Leftrightarrow& 2x=4\ \text{ ou }\ 2x=2\\ \\ &\Leftrightarrow& x=2\ \text{ ou }\ x=1\end{array}$
$$S=\{1\;,\ 2\}$$
b) Résolvons $g(x)=-2x+7$
Sur $]-\infty\;,\ -5]$ on a $g(x)=-4x-13$
alors,
$\begin{array}{rcl} g(x)=-2x+7 &\Leftrightarrow& -4x-13=-2x+7\\ \\ &\Leftrightarrow& -2x=20\\ \\ &\Leftrightarrow& x=-10\in\;]-\infty\;,\ -5]\end{array}$
Donc, $S_{1}=\{-10\}$
Sur $[-5\;,\ 2]$, on a $g(x)=2x+17$
alors,
$\begin{array}{rcl} g(x)=-2x+7 &\Leftrightarrow& 2x+17=-2x+7\\ \\ &\Leftrightarrow& 4x=-10\\ \\ &\Leftrightarrow& x=-\dfrac{10}{4}=-\dfrac{5}{2}\in[-5\;,\ 2]\end{array}$
Donc, $S_{2}=\left\{-\dfrac{5}{2}\right\}$
Sur $[2\;,\ +\infty[$, on a $g(x)=4x+13$
alors,
$\begin{array}{rcl} g(x)=-2x+7 &\Leftrightarrow& 4x+13=-2x+7\\ \\ &\Leftrightarrow& 6x=-6\\ \\ &\Leftrightarrow& x=-1\notin[2\;,\ +\infty[\end{array}$
Donc, $S_{3}=\emptyset$
D'où, $$S=S_{1}\cup S_{2}\cup S_{3}=\left\{-10\;,\ -\dfrac{5}{2}\right\}$$
c) $1\leq f(x)\leq 4$
On a :
$\begin{array}{rcl} 1\leq f(x)\leq 4 &\Leftrightarrow& f(x)\geq 1\ \text{ et }\ f(x)\leq 4\\ \\ &\Leftrightarrow& |2x-3|\geq 1\ \text{ et }\ |2x-3|\leq 4\\ \\ &\Leftrightarrow& (2x-3\geq 1\ \text{ ou }\ 2x-3\leq -1)\ \text{ et }\ (-4\leq 2x-3\leq 4)\\ \\ &\Leftrightarrow& \left(x\geq 2\ \text{ ou }\ x\leq 1\right)\ \text{ et }\ \left(-\dfrac{1}{2} \leq x\leq \dfrac{7}{2} \right)\\ \\ &\Leftrightarrow& x\in\;]-\infty\;,\ 1]\cup[2\;,\ +\infty[ \ \text{ et }\ x\in\left[-\dfrac{1}{2}\;,\ \dfrac{7}{2}\right]\end{array}$
Donc, $$S=\left[-\dfrac{1}{2}\;,\ 1\right]\cup\left[2\;,\ \dfrac{7}{2}\right]$$
d) $\left|\dfrac{x+3}{x}\right|>-1$
On a : $\forall\;x\neq 0\;,\ \left|\dfrac{x+3}{x}\right|$ est toujours positive donc supérieure à -1.
Donc, $$S=\mathbb{R}\setminus\{0\}=\;]-\infty\;,\ 0[\cup]0\;,\ +\infty[$$
III.3 Distance sur une droite et intervalles de $\mathbb{R}$
III.3.1 Définition
Soit $(x'Ox)$ un axe gradué.
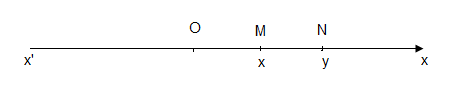
$M$ et $N$ deux points d'abscisses respectives $x$ et $y$. On appelle distance entre les points $M$ et $N$, le nombre positif noté $d(M,\ N)$ vérifiant :$$d(M,\ N)=MN=d(x,\ y)=|x-y|$$
$|x|$ est la distance entre $M$ d'abscisse $x$ et le point $O$ d'abscisse 0;
$MO=d(M\;,\ O)=d(x\;,\ 0)=|x-0|=|x|$.
III.3.2 Propriétés
Soient $x\;,\ y$ et $a$ trois nombre réels, et $r\in\mathbb{R}_{+}$. On a :
$\centerdot\ \ d(x\;,\ y)=d(y\;,\ x);\qquad\qquad (|x-y|=|y-x|)$
$\begin{array}{ccl}\centerdot\ \ d(x\;,\ a)=r&\Leftrightarrow&|x-a|=r\\ \\&\Leftrightarrow&x-a=r\ \mbox{ ou }\ x-a=-r \\ \\&\Leftrightarrow&x=a+r\ \mbox{ ou }\ x=a-r\\ \\&\Leftrightarrow&x\in\{a-r\;;\ a+r\}\end{array}$
$\begin{array}{ccl}\centerdot\ \ d(x\;,\ a)\leq r&\Leftrightarrow&|x-a|\leq r\\ \\&\Leftrightarrow&-r\leq x-a\leq r \\ \\&\Leftrightarrow&a-r\leq x\leq a+r\\ \\&\Leftrightarrow&x\in[a-r\;;\ a+r]\end{array}$
Exemple
Soient $A$ et $B$ deux points sur une droite graduée tels que $x_{A}=-4$ et $y_{B}=3.$
Donner la distance entre $A$ et $B.$
On a $d(A\;,\ B)=|x_{B}-x_{A}|=|3-(-4)|=7$
III.3.3 Intervalles dans $\mathbb{R}$
$-\ $ Intervalles bornés
Soient $a$ et $b$ deux réels tels que $a<b.$
L'ensemble des réels compris entre $a$ et $b$ est un intervalle borné.
$$\begin{array}{ccl} \text{Notation}& &\text{Inégalité}\\ & & \\ [a\;;\ b]& &a\leq x\leq b \\ ]a\;;\ b[& &a<x<b \\ ]a\;;\ b]& &a<x\leq b \\ [a\;;\ b[& &a\leq x<b \end{array}$$
Ces intervalles sont bornés ; $a$ et $b$ sont les bornes.
$-\ $ Centre et rayon d'un intervalle borné
Soit $x_{0}\in[a;\ b]\;;\ x_{0}=\dfrac{a+b}{2}$, alors $x_{0}$ est appelé centre de l'intervalle et le réel noté $r=\dfrac{b-a}{2}$ est le rayon.
$-\ $ Intervalles non bornés
$$\begin{array}{ccl} \text{Notation}& &\text{Inégalité}\\ & & \\ ]-\infty\;;\ a]& &x\leq a \\ ]-\infty\;;\ a[& &x<a \\ ]a\;;\ +\infty[& &x>a \\ [a\;;\ +\infty[& &x\geq a \end{array}$$
$-\ $ Réunion et Intersection d'intervalles
Exemple
Soient $I$ et $J$ deux intervalles de $\mathbb{R}.$
Déterminer $I\cap J$ et $I\cup J$ dans chacun des cas suivants :
a) $I=[-2\;;\ 6]\qquad J=[-3\;;\ +\infty[$
b) $I=]-\infty\;;\ 7]\qquad J=\left[-\dfrac{4}{5}\;;\ +\infty\right[$
c) $I=]-1\;;\ 4]\qquad J=[5\;;\ 10]$
Résolution
Remarques :
Pour l'intersection on hachure les parties non solutions
Pour la réunion on hachure les parties solutions
a)

$I\cap J=[-2\;;\ 6]$

$[-2\;;\ 6]\subset[-3\;;\ +\infty[$ alors $I\cup J=[-3\;;\ +\infty[$
b)
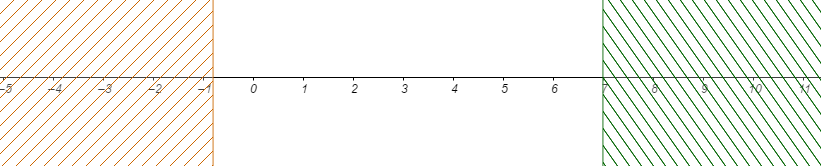
$I\cap J=\left[-\dfrac{4}{5}\;;\ 7\right]$

$I\cup J=\mathbb{R}=]-\infty\;;\ +\infty[$
c)
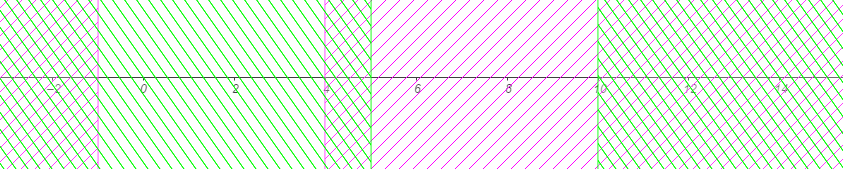
$I\cap J=\emptyset$

$I\cup J=]-1\;;\ 4]\cup[5\;;\ 10]$
V. Ordre et encadrement
V.1 Définition
Soient $a$ et $b$ deux nombres réels. On a :
$\centerdot\ \ a\leq b\ \Leftrightarrow\ a-b\leq 0\ \mbox{ ou }\ b-a\geq 0$
$\centerdot\ \ a>b\ \Leftrightarrow\ a-b>0\ \mbox{ ou }\ b-a<0$
V.2 Propriétés
$a$, $b$ et $c$ trois nombres réels, alors on a :
$\centerdot\ \ $ si $a\leq b\ $ et $\ b\leq a\ $ alors, $\ a=b$
$\centerdot\ \ $ si $a\leq b\ $ et $\ b\leq c\ $ alors, $\ a\leq c$
$\centerdot\ \ $ si $a\leq b\ \forall c\in\mathbb{R};\ \ a+c\leq b+c\ $
$\centerdot\ \ $ si $a>0$, $\ b>0\ $ alors $\ a\geq b\ \Leftrightarrow\ a^{2}\geq b^{2}$
$\centerdot\ \ $ si $a<0$, $\ b<0\ $ alors $\ a\geq b\ \Leftrightarrow\ a^{2}\leq b^{2}$
$\centerdot\ \ $ si $a>0$ et $k>0\ $ alors, $\ ka\geq kb$
$\centerdot\ \ $ si $a>0$ et $k<0\ $ alors, $\ ka\leq kb$
$\centerdot\ \ $ si $0<a<b\ $ alors, $\ \dfrac{1}{a}>\dfrac{1}{b}$
$\centerdot\ \ $ si $a<b<0\ $ alors, $\ \dfrac{1}{a}>\dfrac{1}{b}$
$\centerdot\ \ $ si $a\leq x\leq b$ et $c\leq y\leq d\ $ avec $a\;,\ b\;,\ c$ et $d$ des réels strictement positifs alors on a : $ac\leq xy\leq bd$
Exercice d'application
1) Sachant que $2<x<9\quad 3<y<6$, encadrer
$x+y\;;\ x-y\;;\ \dfrac{x}{y}\;;\ x^{2}$
2) Sachant que $3\leq x\leq 5\quad -4\leq y\leq -1$, encadrer
$x-y\;;\ \dfrac{x}{y}\;;\ xy\;;\ y^{2}$
3) Encadrer $2z\;;\ -3z\;;\ z^{2}$ sachant que $-9<z<5$
Résolution
1) Encadrons $x+y$
On a :
$\begin{array}{rcrclcl} 2<x<9\quad\text{et}\quad 3<y<6 &\Rightarrow& 2+3&<&x+y&<&9+6 \\ &\Rightarrow& 5&<&x+y&<&15 \end{array}$
Encadrons $x-y$
On a :
$\begin{array}{rcrclcl} 3<y<6 &\Rightarrow& -6&<&-y&<&-3 \\ \\&\Rightarrow& 2-6&<&x-y&<&9-3 \\ \\&\Rightarrow& -4&<&x-y&<&6 \end{array}$
Encadrons $\dfrac{x}{y}$
On a :
$\begin{array}{rcrclcl} 3<y<6 &\Rightarrow& \dfrac{1}{3}&>&y&>&\dfrac{1}{6} \\ \\&\Rightarrow& \dfrac{2}{6}&<&\dfrac{x}{y}&<&\dfrac{9}{3} \\ \\&\Rightarrow& \dfrac{1}{3}&<&\dfrac{x}{y}&<&3 \end{array}$
Encadrons $x^{2}$
On a :
$\begin{array}{rcrclcl} 2<x<9 &\Rightarrow& 2^{2}&<&x^{2}&<&9^{2} \\ \\&\Rightarrow& 4&<&x^{2}&<&81 \end{array}$
2) Sachant que $3\leq x\leq 5\quad -4\leq y\leq -1$, encadrons $x-y$
On a :
$\begin{array}{rcrclcl} -4\leq y\leq -1 &\Rightarrow& 1&\leq& -y&\leq& 4 \\ \\&\Rightarrow& 3+1&\leq& x-y&\leq& 5+4 \\ \\&\Rightarrow& 4&\leq& x-y&\leq& 9 \end{array}$
Encadrons $xy$
On a :
$\begin{array}{rcrclcl} -4\leq y\leq -1 &\Rightarrow& 1&\leq& -y&\leq& 4 \\ \\&\Rightarrow& 3\times 1&\leq& -xy&\leq& 5\times 4 \\ \\&\Rightarrow& 3&\leq& -xy&\leq& 20 \\ \\&\Rightarrow& -20&\leq& xy&\leq& -3 \end{array}$
Encadrons $y^{2}$
On a :
$\begin{array}{rcrclcl} -4\leq y\leq -1 &\Rightarrow&1&\leq& -y&\leq& 4 \\ \\&\Rightarrow& 1^{2}&\leq &(-y)^{2}&\leq& 4^{2} \\ \\&\Rightarrow& 1&\leq& y^{2}&\leq& 16 \end{array}$
Encadrons $\dfrac{x}{y}$
On a :
$\begin{array}{rcrclcl} -4\leq y\leq -1 &\Rightarrow& \dfrac{1}{-1}&\leq&\dfrac{1}{y}&\leq& \dfrac{1}{-4} \\ \\&\Rightarrow& \dfrac{1}{4}&\leq&\dfrac{-1}{y}&\leq& \dfrac{1}{1} \\ \\&\Rightarrow& \dfrac{3}{4}&\leq&\dfrac{-x}{y}&\leq& \dfrac{5}{1} \\ \\&\Rightarrow& -\dfrac{5}{1}&\leq&\dfrac{x}{y}&\leq& -\dfrac{3}{4} \\ \\&\Rightarrow& -5&\leq&\dfrac{x}{y}&\leq& -\dfrac{3}{4} \end{array}$
3) Encadrons $2z\;;\ -3z\;;\ z^{2}$
On a :
$-9<z<5\ \Rightarrow\ -18<2z<10$
$-9<z<5\ \Rightarrow\ -15<-3z<27$
$-9<z<5\ \Rightarrow\ 0\leq z^{2}<81$
VI. Valeur approchée - notation scientifique
VI.1 Définition
$\centerdot\ \ $ On dit que $a$ est une valeur approchée de $x$ à $\epsilon$ près si et seulement si $$a-\epsilon\leq x\leq a+\epsilon$$
c'est-à-dire $|x-a|\leq\epsilon$.
$\centerdot\ \ $ On dit que $a$ est une valeur approchée par défaut de $x$ à $\epsilon$ près si, et seulement si, $$a\leq x\leq a+\epsilon$$
$\centerdot\ \ $ On dit que $a$ est une valeur approchée par excès de $x$ à $\epsilon$ près si, et seulement si, $$a-\epsilon\leq x\leq a$$
Exemple
1) Donner un encadrement de $x$ dans les cas suivants :
a) $40.5$ est une valeur approchée à $10^{-1}$ près de $x.$
b) $40.5$ est une valeur approchée à $10^{-2}$ près de $x.$
c) $40.5$ est une valeur approchée à $5.10^{-2}$ près de $x.$
2) Donner un encadrement de $x-y\;;\ xy$ sachant que $2.21$ est une valeur approchée de $x$ à 0.1 près et $-4\leq y\leq -1.$
Résolution
1) a) $$\begin{array}{ccccc} 40.5-0.1&\leq&x&\leq&40.5+0.1 \\ \\40.4&\leq&x&\leq&40.6\end{array}$$
b) $$\begin{array}{ccccc} 40.5-0.01&\leq&x&\leq&40.5+0.01 \\ \\40.49&\leq&x&\leq&40.51\end{array}$$
c) $$\begin{array}{ccccc} 40.5-0.05&\leq&x&\leq&40.5+0.05 \\ \\40.45&\leq&x&\leq&40.55\end{array}$$
2) On a : $-4\leq y\leq -1\ \Rightarrow\ 1\leq -y\leq 4$
Alors,
$$\begin{array}{ccccc} 2.21-0.1&\leq&x&\leq&2.21+0.1 \\ \\2.11&\leq&x&\leq&2.31 \\ \\2.11+1&\leq&x-y&\leq&2.31+4 \\ \\3.11&\leq&x-y&\leq&6.31\end{array}$$
Donc, $3.11\leq x-y\leq 6.31$
$$\begin{array}{ccccc} 2.11\times 1&\leq&-xy&\leq&2.31\times 4 \\ \\2.11&\leq&-xy&\leq&9.24 \\ \\-9.24&\leq&xy&\leq&2.11\end{array}$$
Donc, $-9.24\leq xy\leq 2.11$
$\centerdot\ \ \epsilon$ est appelé incertitude.
En effet, $a$ est une valeur approchée de $x$ à $\epsilon$ près donc en remplaçant $x$ par $a$ on commet une erreur $\Delta x=x-a.$ L'incertitude est un majorant de la valeur de l'erreur $$|\Delta x|=|x-a|<\epsilon$$
Exemple
$x=\dfrac{4}{3}$
On a $1.33<\dfrac{4}{3}<1.34$ c'est à dire $\dfrac{4}{3}\in\;]1.33\;;\ 1.34[$
Donc $\left|\dfrac{4}{3}-1.33\right|<10^{-2}$
$10^{-2}$ est l'incertitude.
$\centerdot\ \ \forall\;x\in\mathbb{R}$ il existe un entier relatif $(b\in\mathbb{Z})$ et un seul tel que $$b\leq x\leq b+1$$
$b$ s'appelle la partie entière de $x$. On note $$E(x)=b$$
$\centerdot\ \ $ Soit $x$ un réel, $n\in\mathbb{N}$, $b$ la partie entière de $x.10^{n}$ alors $$b.10^{-n}\leq x\leq(b+1)10^{-n}$$ est un encadrement de $x$ à $10^{-n}$ près.
$b.10^{-n}$ est appelé approximation décimale de $x.$
Exemple
Soit $x=3.124124124124$, donner une approximation de $x$ à l'ordre 3.
On a :
$$\begin{array}{rcl} x.10^{3}=3124.124124124 &\Rightarrow& E(x.10^{3})=3124\\ \\ &\Rightarrow& 3124\leq x.10^{3}\leq 3125\\ \\ &\Rightarrow& 3124\times 10^{-3}\leq x.10^{3}\times 10^{-3}\leq 3125\times 10^{-3}\\ \\ &\Rightarrow& 3.124\leq x\leq 3.125\end{array}$$
$$\begin{array}{rcl} x.10^{3}=3124.124124124 &\Rightarrow& E(x.10^{3})=3124\\ \\ &\Rightarrow& 3124\leq x.10^{3}\leq 3125\\ \\ &\Rightarrow& 3124\times 10^{-3}\leq x.10^{3}\times 10^{-3}\leq 3125\times 10^{-3}\\ \\ &\Rightarrow& 3.124\leq x\leq 3.125\end{array}$$
$3.124$ est donc une approximation décimale de $x$ à l'ordre 3.
VI.2 Notation scientifique
La notation scientifique d'un nombre réel $x$ est l'écriture de $x$ sous la forme $a.10^{p}$ où $1\leq a\leq 10$ et $p\in\mathbb{Z}.$
Exemple
On donne les écritures scientifiques de $2\,543\;;\ 6\,000\;;\ 0.0064\;;\ 29.77$
On a : $2543=2.543\;10^{3}\;;\quad 6000=6\;10^{3}$
$0.0064=6.4\;10^{-3}\;;\quad 29.77=2.977\;10^{1}$
Auteur:
Diny Faye & Seyni Ndiaye

Commentaires
Anonyme (non vérifié)
sam, 10/20/2018 - 11:08
Permalien
Tres intéressant
Pathé (non vérifié)
mar, 08/27/2019 - 16:51
Permalien
Très important
Anonyme (non vérifié)
sam, 11/02/2019 - 02:18
Permalien
Impressionant
Anonyme (non vérifié)
ven, 11/29/2019 - 17:16
Permalien
Très important
Bassirou gueye (non vérifié)
lun, 11/23/2020 - 23:05
Permalien
Pour mieux comprendre
Bassirou gueye (non vérifié)
lun, 11/23/2020 - 23:07
Permalien
J'aimerai bien de travailler
Bassirou Gueye (non vérifié)
mar, 11/24/2020 - 23:24
Permalien
Calcul dans R
Mouhamadou lami... (non vérifié)
mar, 12/01/2020 - 15:56
Permalien
Très intéressant . Merci
Anonyme (non vérifié)
dim, 02/28/2021 - 00:13
Permalien
Calcul dans R
Ndeye Fatou Ndiaye (non vérifié)
lun, 10/18/2021 - 18:28
Permalien
merici beaucoup
Moussa Sow (non vérifié)
mar, 05/31/2022 - 19:53
Permalien
Bonjour pourquoi il n y a
Anonyme (non vérifié)
ven, 10/28/2022 - 15:15
Permalien
c bien
Anonyme (non vérifié)
dim, 11/06/2022 - 20:34
Permalien
Merci
dièye (non vérifié)
mer, 06/07/2023 - 15:44
Permalien
vous pouvez mettre pour
dièye (non vérifié)
mer, 06/07/2023 - 15:44
Permalien
vous pouvez mettre pour
mayé faye (non vérifié)
ven, 10/13/2023 - 19:53
Permalien
merci beaucoup
mayé faye (non vérifié)
ven, 10/13/2023 - 21:29
Permalien
eleve
Sadaga Manel Fall (non vérifié)
mar, 10/17/2023 - 21:26
Permalien
Merci
Anonyme (non vérifié)
mer, 10/18/2023 - 15:30
Permalien
Maths 2S
Anonyme (non vérifié)
mer, 10/18/2023 - 15:31
Permalien
Ok
Serge Herman Sossou (non vérifié)
sam, 10/28/2023 - 23:30
Permalien
Très intéressant
Mouhamed pam (non vérifié)
mar, 11/07/2023 - 20:28
Permalien
Le contenue est riche
Sassy (non vérifié)
sam, 10/12/2024 - 16:58
Permalien
Il y'a un erreur au niveau du
Anonyme (non vérifié)
jeu, 11/07/2024 - 18:00
Permalien
au niveau du développement de
Anonyme (non vérifié)
dim, 10/26/2025 - 21:59
Permalien
non ,la faute ne se trouve
Djimranodji maxime (non vérifié)
jeu, 11/21/2024 - 06:25
Permalien
Comment télécharger le cour
Anonyme (non vérifié)
jeu, 10/23/2025 - 22:23
Permalien
bonjour , veuillez donner les
Ajouter un commentaire