Corrigé devoir n° 3 maths - 3e

Classe: 
Troisième
 

Exercice 1

1) les solutions de l'équation $x^{2}=36$ sont $-6\ $ et $\ 6$
 
2) Le carrée d'un nombre est égale à $6.$ Ce nombre est $\sqrt{6}$
 
3) Le $PGCD$ de deux nombres est le plus grand diviseur commun de ces deux nombres
 
4) l'image d'un cercle par une translation est un cercle de même rayon
 
5) Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres cotés

Exercice 2

1) Calculons $A=\dfrac{5}{3}\div\left(\dfrac{1}{4}+\dfrac{5}{7}\right)$
 
On a alors :
 
$\begin{array}{rcl} A&=&\dfrac{5}{3}\div\left(\dfrac{1}{4}+\dfrac{5}{7}\right)\\\\&=&\dfrac{5}{3}\div\left(\dfrac{7}{28}+\dfrac{20}{28}\right)\\\\&=&\dfrac{5}{3}\div \dfrac{27}{28}\\\\&=&\dfrac{5}{3}\times\dfrac{28}{27}\\\\&=&\dfrac{140}{81}\end{array}$
 
D'où, $\boxed{A=\dfrac{140}{81}}$
 
2) On donne : $B=\dfrac{42\times 10^{7}\times 5\times 10^{-7}}{25\times 10^{-6}}$
 
Calculons $B$ et donnons le résultat sous la forme $a\times 10^{p}$
 
On a :
 
$\begin{array}{rcl} B&=&\dfrac{42\times 10^{7}\times 5\times 10^{-7}}{25\times 10^{-6}}\\\\&=&\dfrac{42\times 5\times 10^{7}\times 10^{-7}\times 10^{6}}{25}\\\\&=&\dfrac{42\times 10^{6}}{5}\\\\&=&\dfrac{42}{5}\times 10^{6}\end{array}$
 
Ainsi, $\boxed{B=\dfrac{42}{5}\times 10^{6}}$
 
3) Écrivons sous la forme $a\sqrt{b}$ l'expression $C=2\sqrt{48}+\sqrt{75}-3\sqrt{12}$
 
On a :
 
$\begin{array}{rcl} C&=&2\sqrt{48}+\sqrt{75}-3\sqrt{12}\\\\&=&2\sqrt{16\times 3}+\sqrt{25\times 3}-3\sqrt{4\times 3}\\\\&=&2\times\sqrt{16}\times\sqrt{3}+\sqrt{25}\times\sqrt{3}-3\times\sqrt{4}\times\sqrt{3}\\\\&=&2\times 4\times\sqrt{3}+5\times\sqrt{3}-3\times 2\times\sqrt{3}\\\\&=&8\sqrt{3}+5\sqrt{3}-6\sqrt{3}\\\\&=&7\sqrt{3}\end{array}$
 
Donc, $\boxed{C=7\sqrt{3}}$
 
4) Développons, réduisons et ordonnons $D=(5\sqrt{2}+3)(4\sqrt{2}-7)$
 
Soit :
 
$\begin{array}{rcl} D&=&(5\sqrt{2}+3)(4\sqrt{2}-7)\\\\&=&5\times\sqrt{2}\times\sqrt{2}-7\times 5\sqrt{2}+3\times 4\sqrt{2}-3\times 7\\\\&=&5\times 2-35\sqrt{2}+12\sqrt{2}-21\\\\&=&10-23\sqrt{2}-21\\\\&=&-11-23\sqrt{2}\end{array}$
 
Ainsi, $\boxed{D=-11-23\sqrt{2}}$
 
5) Écrivons $E$ sans radical au dénominateur $E=\dfrac{4}{2+\sqrt{3}}$
 
On a :
 
$\begin{array}{rcl} E&=&\dfrac{4}{2+\sqrt{3}}\\\\&=&\dfrac{4(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}\\\\&=&\dfrac{8-4\sqrt{3}}{(2^{2}-(\sqrt{3})^{2})}\\\\&=&\dfrac{8-4\sqrt{3}}{4-3}\\\\&=&8-4\sqrt{3}\end{array}$
 
D'où, $\boxed{D=8-4\sqrt{3}}$
 
6) Déterminons le $PGCD(42\;;\ 56)$
 
En décomposant en produits de facteurs premiers $42\ $ et $\ 56$, on obtient :
 
$42=2\times 3\times 7\ $ et $\ 56=2^{3}\times 7$
 
Par suite, $PGCD(42\;;\ 56)=2\times 7=14$

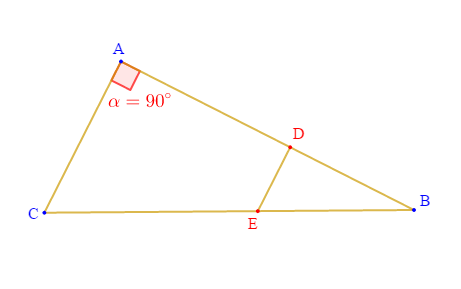
Exercice 3

La charpente d'un toit est schématisé par la figure suivante.
 
 
Soit $(DE)$ parallèle à $(AC)$ et on donne :
$$AC=3\:;\quad BC=5\quad\text{et}\quad BE=2$$
1) Oui on peut bien utiliser la propriété de THALÈS pour calculer $DE$
 
Justifions notre réponse.
 
En effet, les droites $(AB)\ $ et $\ (BC)$ sécantes en $B$ sont coupées par la sécante $(DE)$ qui est parallèle à la droite $(AC).$
 
Donc, les triangles $ABC\ $ et $\ BDE$ sont en position de Thalès.
 
D'où, on peut appliquer le théorème de Thalès pour calculer $DE.$
 
2) Calculons $DE$
 
En appliquant le théorème de Thalès, on a :
$$\dfrac{DE}{AC}=\dfrac{BE}{BC}$$
Ce qui donne :
 
$\begin{array}{rcl} DE&=&\dfrac{BE}{BC}\times AC\\\\&=&\dfrac{2}{5}\times 3\\\\&=&\dfrac{6}{5}\\\\&=&1.2\end{array}$
 
D'où, $\boxed{DE=1.2}$
 
3) En utilisant la propriété de Pythagore dans le triangle $ABC$, calculons $AB.$
 
Le triangle $ABC$ étant rectangle en $A$ alors, en appliquant le théorème de Pythagore, on obtient :
$$BC^{2}=AC^{2}+AB^{2}$$
Par suite, $AB^{2}=BC^{2}-AC^{2}$
 
Ainsi,
 
$\begin{array}{rcl} AB&=&\sqrt{BC^{2}-AC^{2}}\\\\&=&\sqrt{5^{2}-3^{2}}\\\\&=&\sqrt{25-9}\\\\&=&\sqrt{16}\\\\&=&4\end{array}$
 
D'où, $\boxed{AB=4}$
 
4) Calculons $AD.$
 
En utilisant une conséquence du théorème de Thalès, on obtient :
$$\dfrac{AD}{AB}=\dfrac{CE}{BC}$$
Donc, $AD=\dfrac{CE}{BC}\times AB$
 
Or, $CE=BC-BE=5-2=3$
 
Par suite,
 
$\begin{array}{rcl} AD&=&\dfrac{CE}{BC}\times AB\\\\&=&\dfrac{3}{5}\times 4\\\\&=&\dfrac{12}{5}\\\\&=&2.4\end{array}$
 
D'où, $\boxed{AD=2.4}$

 

Auteur: 
Diny Faye

Commentaires

Abdoulaye (non vérifié)

ven, 01/12/2024 - 23:20

BFEM

Ajouter un commentaire