Corrigé devoir n° 5 maths - 5e

 

1) Recopions et complétons :

 

a) $N'$ symétrique du point $N$ par rapport à $O$ signifie que $O$ est le milieu du segment $[NN']$

 

b) Si $[IJ]\ $ et $\ [KL]$ sont symétriques par rapport à un point alors, $IJ=KL$

 

2) Donnons la définition des termes suivants :

 

$-\ $ angles alternes-internes : deux angles sont alternes internes si, et seulement si :

 

$\centerdot\ $ ils n'ont pas de sommet commun

 

$\centerdot\ $ ils sont tous à l'intérieur de la bande délimitée par deux droites coupées par une sécante

 

$\centerdot\ $ ils sont également situés de part et d'autres de la sécante

 

$-\ $ nombre premier : un nombre est dit premier si, et seulement si, il n'est divisible que par un $(1)$ et lui même.

 

$-\ $ angles adjacents : deux angles adjacents sont deux angles qui ont un sommet commun et sont situés de part et d'autre d'un côté commun.

 

$-\ $ angles supplémentaires : deux angles supplémentaires sont deux angles dont la somme de leur mesure est égale à $180^{\circ}.$

1) Écrivons chacune des expressions suivantes sous la forme de puissances premières.

$$A=(2\times 3)^{4}\times 2^{4}\times 3^{5}\qquad B=2^{4}\times(3^{2})^{3}\times 2^{6}\times 3^{2}\times 2^{0}$$

Soit :

 

$\begin{array}{rcl} A&=&(2\times 3)^{4}\times 2^{4}\times 3^{5}\\\\&=&2^{4}\times 3^{4}\times 2^{4}\times 3^{5}\\\\&=&2^{4}\times 2^{4}\times 3^{4}\times 3^{5}\\\\&=&2^{4+4}\times 3^{4+5}\\\\&=&2^{8}\times 3^{9}\end{array}$

 

Ainsi, $\boxed{A=2^{8}\times 3^{9}}$

 

On a :

 

$\begin{array}{rcl} B&=&2^{4}\times(3^{2})^{3}\times 2^{6}\times 3^{2}\times 2^{0}\\\\&=&2^{4}\times 3^{2\times 3}\times 2^{6}\times 3^{2}\times 2^{0}\\\\&=&2^{4}\times 3^{6}\times 2^{6}\times 3^{2}\times 2^{0}\\\\&=&2^{4}\times 2^{6}\times 2^{0}\times 3^{6}\times 3^{2}\\\\&=&2^{4+6+0}\times 3^{6+2}\\\\&=&2^{10}\times 3^{8}\end{array}$

 

Donc, $\boxed{B=2^{10}\times 3^{8}}$

 

2) Calculons en respectant les règles de priorités :

 

$\begin{array}{rcl} C&=&10.5-3\times(4-3)^{3}+3\times (14-5\div 2)\\\\&=&10.5-3\times 1^{3}+3\times (14-2.5)\\\\&=&10.5-3+3\times 11.5\\\\&=&7.5+34.5\\\\&=&42\end{array}$

 

Ainsi, $\boxed{C=42}$

 

3) a) Calculons chacune des expressions $A\;;\ B\;;\ C\ $ et $\ D$ puis simplifions les résultats.

$$A=\dfrac{9}{4}+\dfrac{5}{3}-\dfrac{5}{12}\qquad B=\left(\dfrac{8}{3}+\dfrac{5}{2}\right)\times 4$$

$$C=\left(\dfrac{4}{5}-\dfrac{1}{2}\right)\div 2\qquad D=\dfrac{1}{4}\times\dfrac{7}{2}+\dfrac{9}{5}$$

On a :

 

$\begin{array}{rcl} A&=&\dfrac{9}{4}+\dfrac{5}{3}-\dfrac{5}{12}\\\\&=&\dfrac{27}{12}+\dfrac{20}{12}-\dfrac{5}{12}\\\\&=&\dfrac{27+20-5}{12}\\\\&=&\dfrac{42}{12}\\\\&=&\dfrac{6\times 7}{6\times 2}\\\\&=&\dfrac{7}{2}\end{array}$

 

D'où, $\boxed{A=\dfrac{7}{2}}$

 

Soit :

 

$\begin{array}{rcl} B&=&\left(\dfrac{8}{3}+\dfrac{5}{2}\right)\times 4\\\\&=&\left(\dfrac{16}{6}+\dfrac{15}{6}\right)\times 4\\\\&=&\left(\dfrac{16+15}{6}\right)\times 4\\\\&=&\dfrac{31}{6}\times 4\\\\&=&\dfrac{31\times 4}{6}\\\\&=&\dfrac{31\times 2\times 2}{3\times 2}\\\\&=&\dfrac{62}{3}\end{array}$

 

Donc, $\boxed{B=\dfrac{62}{3}}$

 

On a :

 

$\begin{array}{rcl} C&=&\left(\dfrac{4}{5}-\dfrac{1}{2}\right)\div 2\\\\&=&\left(\dfrac{8}{10}-\dfrac{5}{10}\right)\div 2\\\\&=&\left(\dfrac{8-5}{10}\right)\div 2\\\\&=&\dfrac{3}{10}\div 2\\\\&=&\dfrac{3}{10}\times \dfrac{1}{2}\\\\&=&\dfrac{3}{20}\end{array}$

 

D'où, $\boxed{C=\dfrac{3}{20}}$

 

On a :

 

$\begin{array}{rcl} D&=&\dfrac{1}{4}\times\dfrac{7}{2}+\dfrac{9}{5}\\\\&=&\dfrac{7}{8}+\dfrac{9}{5}\\\\&=&\dfrac{35}{40}+\dfrac{72}{40}\\\\&=&\dfrac{35+72}{40}\\\\&=&\dfrac{107}{40}\end{array}$

 

Donc, $\boxed{D=\dfrac{107}{40}}$

 

b) Mettons ces résultats sous la forme de $q+\dfrac{r}{b}$

 

On a : $A=\dfrac{7}{2}$

 

Donc, on peut écrire :

 

$\begin{array}{rcl} A&=&\dfrac{6+1}{2}\\\\&=&\dfrac{6}{2}+\dfrac{1}{2}\\\\&=&3+\dfrac{1}{2}\end{array}$

 

D'où, $\boxed{A=3+\dfrac{1}{2}}$

 

Soit : $B=\dfrac{62}{3}$ alors, on a :

 

$\begin{array}{rcl} B&=&\dfrac{60+2}{3}\\\\&=&\dfrac{60}{3}+\dfrac{2}{3}\\\\&=&20+\dfrac{2}{3}\end{array}$

 

Ainsi, $\boxed{B=60+\dfrac{2}{3}}$

 

On a : $C=\dfrac{3}{20}$

 

Alors, on peut écrire :

 

$\begin{array}{rcl} C&=&\dfrac{20-17}{20}\\\\&=&\dfrac{20}{20}-\dfrac{17}{20}\\\\&=&1-\dfrac{17}{20}\\\\&=&1+\left(\dfrac{-17}{20}\right)\end{array}$

 

Donc, $\boxed{C=1+\left(\dfrac{-17}{20}\right)}$

 

Soit : $D=\dfrac{107}{40}$ alors, on a :

 

$\begin{array}{rcl} D&=&\dfrac{80+27}{40}\\\\&=&\dfrac{80}{40}+\dfrac{27}{40}\\\\&=&2+\dfrac{27}{40}\end{array}$

 

D'où, $\boxed{D=2+\dfrac{27}{40}}$

 

3) Rendons irréductibles les fractions suivantes :

$$\dfrac{256}{224}\;;\quad\dfrac{450}{180}$$

En décomposant $256\ $ et $\ 224$ en produits de facteurs premiers, on obtient :

 

$256=2^{8}\ $ et $\ 224=2^{5}\times 7$

 

Ainsi,

 

$\begin{array}{rcl} PGCD(256\;;\ 224)&=&2^{5}\\\\&=&32\end{array}$

 

Par suite,

 

$\begin{array}{rcl} \dfrac{256}{224}&=&\dfrac{256\div 32}{224\div 32}\\\\&=&\dfrac{8}{7}\end{array}$

 

D'où, $\boxed{\dfrac{256}{224}=\dfrac{8}{7}}$

 

De la même manière, en décomposant $450\ $ et $\ 180$ en produits de facteurs premiers, on obtient :

 

$450=2\times 3^{2}\times 5^{2}\ $ et $\ 180=2^{2}\times 3^{2}\times 5$

 

Ainsi,

 

$\begin{array}{rcl} PGCD(450\;;\ 180)&=&2\times 3^{2}\times 5\\\\&=&90\end{array}$

 

Par suite,

 

$\begin{array}{rcl} \dfrac{450}{180}&=&\dfrac{450\div 90}{180\div 90}\\\\&=&\dfrac{5}{2}\end{array}$

 

D'où, $\boxed{\dfrac{450}{180}=\dfrac{5}{2}}$

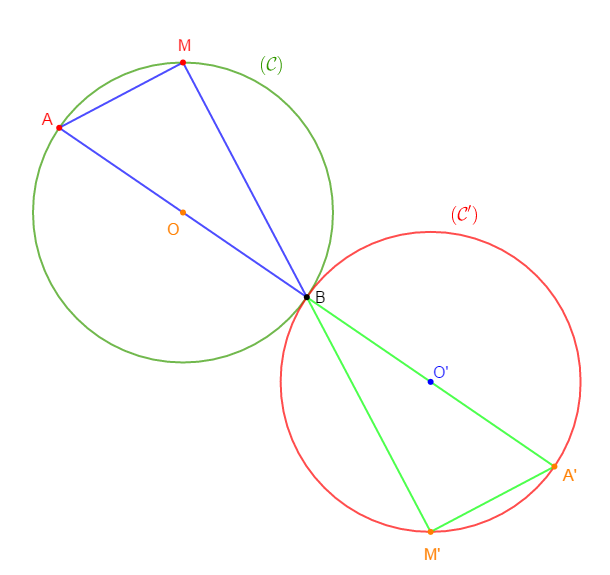
1) Construisons un cercle $(\mathcal{C})$ de centre $O$ et de rayons $r=3\;cm$

 

2) Marquons un diamètre $[AB]$ puis un point $M$ sur le cercle tel que $M\neq A\ $ et $\ M\neq B$

 

3) Construisons le cercle $(\mathcal{C}')$ de centre à $O'$ symétrique de $(\mathcal{C})$ par rapport à $B.$

 

La mesure du rayon du cercle $(\mathcal{C}')$ est :

$$r'=3\;cm$$

Rappel : le symétrique d'un cercle par rapport à un point est un cercle de même rayon.

 

4) Construisons le triangle $A'B'M'$ symétrique de $ABM$ par rapport à $B$

Dans la figure ci-dessous, $(AB)\ $ et $\ (CG)$ sont deux droites parallèles.

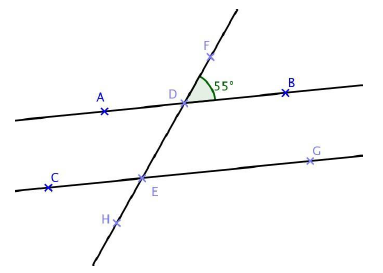
1) Les angles $\widehat{FDB}\ $ et $\ \widehat{ADE}$ sont opposés par le sommet $D.$

 

Ils ont donc, la même mesure.

 

D'où, $\widehat{ADE}=55^{\circ}$

 

2) Les angles $\widehat{ADE}\ $ et $\ \widehat{EDB}$ sont adjacents et supplémentaires.

 

Donc, $\widehat{ADE}+\widehat{EDB}=180^{\circ}$

 

Par suite,

 

$\begin{array}{rcl}\widehat{EDB}&=&\widehat{ADE}+\widehat{EDB}=180^{\circ}-\widehat{ADE}\\\\&=&180^{\circ}-55^{\circ}\\\\&=&125^{\circ}\end{array}$

 

Ainsi, $\widehat{EDB}=125^{\circ}$

 

3) a) $\widehat{EDB}\ $ et $\ \widehat{CED}$ sont deux angles alternes-internes.

 

b) Donnons la mesure de ces angles en justifiant notre réponse.

 

$(AB)\ $ et $\ (CG)$ étant deux droites parallèles coupées par une sécante $(FH)$ alors, les angles alternes-internes $\widehat{EDB}\ $ et $\ \widehat{CED}$ sont de même mesure.

 

D'où, $\widehat{EDB}=\widehat{CED}=125^{\circ}$

 

4) a) $\widehat{FDB}\ $ et $\ \widehat{DEG}$ sont deux angles correspondants.

 

b) Donnons la mesure de ces angles en justifiant notre réponse.

 

Comme $(AB)\ $ et $\ (CG)$ sont deux droites parallèles coupées par une sécante $(FH)$ alors, les angles correspondants $\widehat{FDB}\ $ et $\ \widehat{DEG}$ sont de même mesure.

 

Ainsi, $\widehat{FDB}=\widehat{DEG}=55^{\circ}$