Classe:

Troisième

Exercice 1

Écrire les expressions suivantes sous la forme $x\sqrt{a}+y\sqrt{b}$ où $x\ $ et $\ y$ sont des réels et $a\ $ et $\ b$ des entiers naturels :

$A=\sqrt{\dfrac{1}{2}}+(\sqrt{2})^{3}-7\sqrt{3}+\sqrt{72}+\sqrt{\dfrac{81}{3}}$

$B=\sqrt{200}-5\sqrt{\dfrac{75}{2}}+\dfrac{3}{2}\sqrt{54}-\sqrt{32}$

$C=5\sqrt{20}+\dfrac{3}{2}\sqrt{\dfrac{9}{5}}-2\sqrt{343}+10\sqrt{28}$

Exercice 2

Calculer les expressions suivantes tout en rendant rationnel le dénominateur :

$X=\dfrac{3\sqrt{2}-4\sqrt{5}}{\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{3}}\qquad\quad Y=\dfrac{2\sqrt{3}+3\sqrt{2}}{-2\sqrt{3}-3\sqrt{2}}$

$Z=\dfrac{\sqrt{7}-\sqrt{5}}{\sqrt{\dfrac{2}{3}}}\qquad\quad T=\dfrac{\dfrac{2\sqrt{5}-3\sqrt{11}}{4\sqrt{3}+\sqrt{7}}}{\sqrt{\dfrac{3}{2}}}$

Exercice 3

Soit un réel $a\ $ tel que : $a=1+\sqrt{\dfrac{1}{2}}$ et soit $b$ son expression conjuguée.

1) déterminer $b$ puis calculer $(a+b)^{2}$

2) Montrer que $2ab=1$ et déduire alors l'expression de $a^{2}+b^{2}$

Exercice 4

On considère deux cercle $\mathcal{C}(O\;,\ 2.5)\ $ et $\ \mathcal{C}'(O'\;,\ 2)$ sécantes en $B\ $ et $\ C.$

Soit $\mathcal{(D)}$ la droite passant par $B$ et parallèle à $(AO).$

La droite passant par $C$ et parallèle à la droite $(O'B)$ coupe $(OA)$ en $I\;,\ (AB)$ en $J$ et $(\mathcal{D})$ en $K.$ On donne $O'I=1.6$

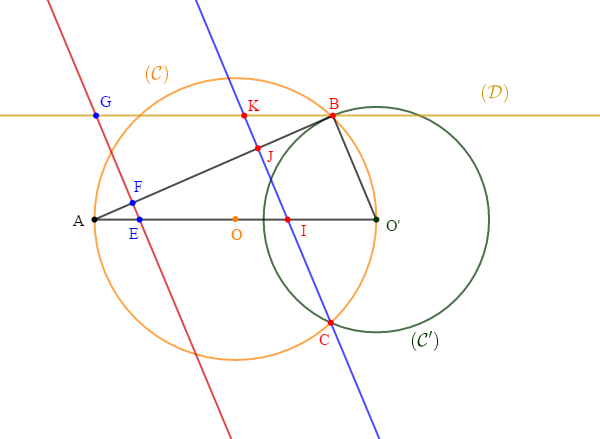
1) Calculer $AB\;;\ BK\ $ et $\ BJ$

2) Soit $E\in[AO]\ $ et $\ F\in[AJ]$ tels que :

$$AE=x\quad\text{et}\quad AF=\dfrac{x\sqrt{21}}{5}$$

La droite passant par $E\ $ et $\ F$ coupe $(\mathcal{D})$ en $G$

Montrer que $(EG)$ est parallèle à $(O'B)$

3) En déduire que $(EG)$ est parallèle à $(IJ)$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction Devoir}}\end{array}$

Auteur:

Diny Faye

Commentaires

RAMZO (non vérifié)

jeu, 03/12/2020 - 21:55

Permalien

Me traiter un exercice

Soit(c) le cercle de centre o de diamètre AB=8 et E un point du cercle tel que AE=6,8.Construis ce cercle. Compare les angles AOB ET AEB.En deduire la nature du triangle ABE? Soit M un point du cercle(c) appatenant à l'arc AE. Compare les angles BME et EAB. a)Calcule la longueur de BE et sinEAB. b)En deduire la mesure de l'angle EAB arrondie au degrè près. Montre que le triangle OEA est isocèle, précise son sommet principal. Détermine les mesures des angles AEO et AOE en justifiant tes reponses. Calcule la longueur exacte de l'arc AE