Devoir n° 2 maths - 3e

Classe: 
Troisième
 

Exercice 1

On donne : $A=3-\sqrt{2}\;,\quad B=\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}\ $ et $\ C=\dfrac{1}{11-6\sqrt{2}}$
 
1) Montrer que $B\ $ et $\ C$ sont des inverses
 
2) Calculer $A^{2}$ puis donner une écriture simplifiée de $\sqrt{C}$
 
3) Donner un encadrement de $\sqrt{C}$ à $10^{-2}$ près, sachant que $1.414<\sqrt{2}<1.415$
 

Exercice 2

Soit $X=\dfrac{\dfrac{3\sqrt{2}}{2}-2}{\sqrt{3}-2}-\left(4-3\sqrt{\dfrac{3}{2}}\right)\ $ et $\ Y=30-12\sqrt{6}$
 
1) Montrer que $X$ peut s'écrire sous la forme $a\sqrt{2}+b\sqrt{3}$ où $a\ $ et $\ b$ sont des entiers relatifs.
 
2) Déduire une écriture plus simplifiée de $X^{2}$
 
3) Calculer $\sqrt{Y}$
 
4) On pose $Z=\dfrac{X}{Y}$
 
Donner une écriture simplifiée puis un encadrement de $Z$ à $10^{-3}$ près, sachant que $1.414<\sqrt{2}<1.415\ $ et $\ 1.732<\sqrt{3}<1.733$
 

Exercice 3

Soit $A=\sqrt{\left(x-\dfrac{3}{2}\right)^{2}}-\dfrac{1}{2}$
 
1) Donner une écriture plus simplifiée de $A$
 
2) Soit $f$ une application affine définie dans $\mathbb{R}$ par :
$$f(x)=\left|x-\dfrac{3}{2}\right|-\dfrac{1}{2}$$
 
Montrer que $f$ est une application affine par intervalles
 
3) Représenter graphiquement $f(x)$ dans l'intervalle $\left[-3\;;\ 3\right]$
 
4) Déduire la solution de l'équation $\left|x-\dfrac{3}{2}\right|=\dfrac{1}{2}$ sur l'intervalle $\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right].$
 

Exercice 4

On considère un triangle $ABC$ tel que :
$$AB=c\;,\ AC=b\ \text{ et }\ BC=6\;cm$$

 

 
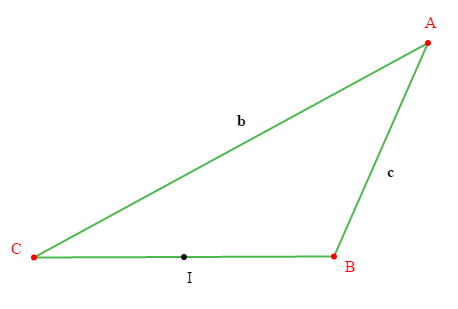
1) Tracer deux cercle $\mathcal{C}_{1}\left(A\;,\ \dfrac{b}{3}\right)\ $ et $\ \mathcal{C}_{2}\left(B\;,\ \dfrac{c}{3}\right)$
 
2) Soit $I$ milieu de $[BC]$, la droite $(\mathcal{D})$ passant par $I$ et parallèle à $(AB)$ coupe $(AC)$ en $J.$
 
Montrer que $J$ est milieu de $[AC]$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction Devoir}}\end{array}$

Auteur: 
Diny Faye

Commentaires

Ndiaye Lô Rokhaya (non vérifié)

sam, 12/21/2019 - 00:38

Puis-avoir la correction de l'exercice1

Matar fall (non vérifié)

jeu, 01/28/2021 - 17:58

Vous êtes les meilleurs

BOLOL (non vérifié)

dim, 12/17/2023 - 15:04

FORMIDABLE

Mamista Tounkara (non vérifié)

mer, 06/26/2024 - 02:06

Vous êtes meilleur

Ajouter un commentaire