Sur la figure  codée ci-dessous, $ABCD$ est un rectangle tel que : $AB=12\ $ et $\ BC=7.$

 

$E$ est un point du segment $[AD]$ tel que $AE=5.$ La droite $(BE)$ coupe $(DC)$ en $F.$

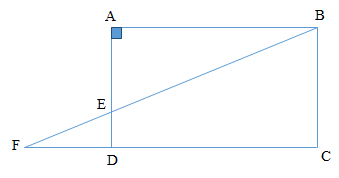
1) Calculer $ED\ $ et $\ EB.$

 

2) Calculer $EF$  en utilisant la conséquence de THALÈS

 

3) On prend $EB=13$

 

4) a) Calculer $\sin\widehat{ABE}$

 

b) Calculer  $\cos\widehat{AEB}$

 

Cet exercice est un questionnaire à choix multiple $(QCM).$ Pour chacune des affirmations, une seule des trois propositions est exacte. Le candidat indiquera sur sa copie, le numéro de l'affirmation et la lettre de la proposition choisie.
$$\begin{array}{|c|l|c|c|c|} \hline N^{\circ}&\qquad\quad\text{Questions}&\text{Réponse A}&\text{Réponse B}&\text{Réponse C}\\ \hline 1&F=\dfrac{(3-2x)(x-1)}{x-1}&F=0&F=1&\text{On ne peut pas}\\ &\text{pour }x=1\text{ alors :}&&&\text{calculer} \\ \hline &\text{La distance}&&&\\ 2&\text{de }\ 3\ \text{ et }\ \sqrt{2}&|3-\sqrt{2}|&1&\sqrt{2}-3 \\ &\text{est :}&&& \\ \hline &A(-12\;;\ 3)\text{ et }B(-5\;;\ 4).&&&\\ 3&\text{Les coordonnées}&(-7\;;\ -1)&(7\;;\ 1)&(-17\;;\ 7)\\ &\text{du vecteur }\overrightarrow{AB}\text{ sont :}&&&\\ \hline 4&\cos 0^{\circ}\text{ est égal à :}&1&0&\text{n'existe pas}\\ \hline&\text{La réunion}&&&\\5&\text{des intervalles}&\emptyset&[0\;;\ 12]&]-\infty\;;\ 0]\cup[2\;;\ 12]\\ &]-\infty\;;\ 0]\text{ et }[2\;;\ 12]\text{ est :}&&&\\ \hline \end{array}$$

On donne :

 

$A=\dfrac{4}{3}-\dfrac{1}{8}\times\left(\dfrac{2}{5}+3\right)\;;\ B=(3-\sqrt{5})^{2}+2(25+\sqrt{45})\ $ et $\ C=\dfrac{-2.4\times 10^{2}\times 5\times 10^{-9}}{3\times 10^{-3}}$

 

1) Calculer $A$ et donner le résultat sous forme de fraction irréductible

 

2) Calculer $B$ et donner le résultat sous la forme la plus simple possible

 

3) Calculer $C$ et donner son écriture scientifique

 

1) On donne l'expression $E=(2x+3)^{2}+(2x+3)(x-6)$

 

a) Développer, ordonner puis réduire $E.$

 

b) Factoriser $E.$

 

2) Calculer $E$ pour $x=0$ puis pour $x=\sqrt{3}.$

 

3) Trouver le réel $x$ pour que : $(5x+7)(x-1)=0$

 

4) Soit $F=\dfrac{2x+7}{x+1}$

 

a) Donner la valeur de $F$ pour $x=\sqrt{2}$

 

b) Écrire $F$ sans radical au dénominateur