Devoir n° 6 maths - 4e
Classe:
Quatrième
Exercice 1
1) Développer, réduire et ordonner les expressions suivantes :
$A=(x+1)(x+2)-5(x^{2}+4x+4)$
$B=(x+2)(2x+5)-(8x+3)^{2}$
2) Factoriser les expressions suivantes :
$C=(3x-2)^{2}-(x+3)^{2}$
$D=(3x-5)(2x+3)+(5-3x)(x+2)$
$E=(3x+5)(2x-1)+9x^{2}-30x+25$
$F=9x^{2}-6x+1-(12x-4)$
3) On considère les expressions suivantes :
$A(x)=(x+2)(x+3)+5x(x+2)$
$B(x)=(x^{2}-4)-(x+2)$
a) Développer, réduire et ordonner $A(x)\ $ et $\ B(x).$
b) Factoriser $A(x)\ $ et $\ B(x).$
c) Calculer la valeur numérique de $A$ et de $B$ Pour $x=0$, Pour $x=(-2).$
Exercice 2
1) A quelles conditions les nombres positifs de $a\;,\ b\ $ et $\ c$ sont les longueurs des côtés d'un triangle ?
2) Soit $(D)$ la médiatrice d'un segment $[AB]$
Si un point $M$ est situé du même coté de $A$ par rapport à $(D)$ , compare $AM$ et $BM$
3) Trace un segment $[AB]$ et construit la médiatrice $(D).$
Marque un point $Q$ tel que $AQ<BQ.$
On appelle le point $M$ le point d'intersection de $(D)\ $ et $\ (BQ).$
Justifie que $AQ+BQ>AM+BM$
Exercice 3
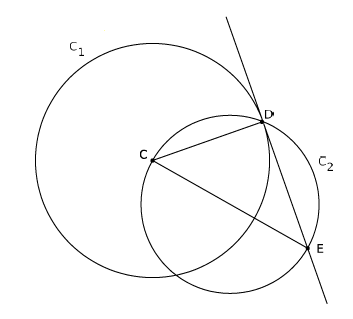
Sur la figure ci-dessous, $C$ est le centre du cercle $C_{1}$, et $\ [CE]$ est un diamètre du cercle $C_{2}.$
Démontrer que $(DE)$ est tangente au cercle $C_{1}\ $ en $\ D.$
Auteur:
Younousse Sèye

Commentaires
Mame Diarra cissé (non vérifié)
mar, 05/18/2021 - 08:17
Permalien
Maths
Falel Mbow (non vérifié)
dim, 02/02/2025 - 07:22
Permalien
La correction
atito (non vérifié)
mar, 06/22/2021 - 00:14
Permalien
J AIME BIEN CE DEVOIRE
Ibrahima Diop (non vérifié)
mar, 05/10/2022 - 17:35
Permalien
PC
Ndeye Khar sock (non vérifié)
sam, 06/18/2022 - 19:28
Permalien
Corrigé
Ndeye Khar sock (non vérifié)
sam, 06/18/2022 - 19:29
Permalien
Tous les matières
Ajouter un commentaire