Exercices : Les angles 5e
Classe:
Cinquième
Exercice 1
Soit $AOB$ un angle aigu.
1) Construire le point $C$ symétrique de $A$ par rapport au sommet $O.$
2) Construire le point $D$ symétrique de $B$ par rapport au sommet $O.$
3) Que peut-on dire des demi-droite $[OA)\ $ et $\ [OC)\ ?$ $\ [OB)\ $ et $\ [OD)\ ?$
4) Que peut-on dire des angles $AOB\ $ et $\ COD\ ?$ $\ COB\ $ et $\ AOD\ ?$
Exercice 2
On considère la figure ci-dessous tel que $mes\;\widehat{x'Oy}=60^{\circ}.$
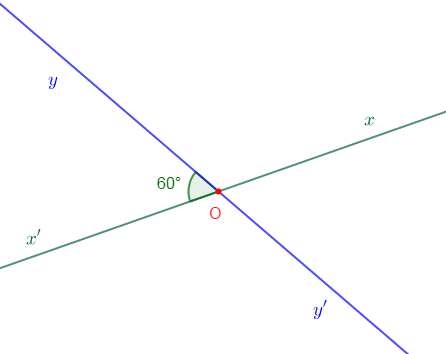
Après avoir reproduire la figure, déterminer :
$mes\;\widehat{xOy'}\;;\ mes\;\widehat{xOy}\ $ et $\ mes\;\widehat{x'Oy'}$
Exercice 3
On considère la figure ci-dessous : $(DC)\ $ et $\ (HF)$ sont parallèles. La droite $(AG)$ coupe $(DC)$ en $B\ $ et $\ (HF)$ en $E$ tel que $mes\;\widehat{ABC}=50^{\circ}.$
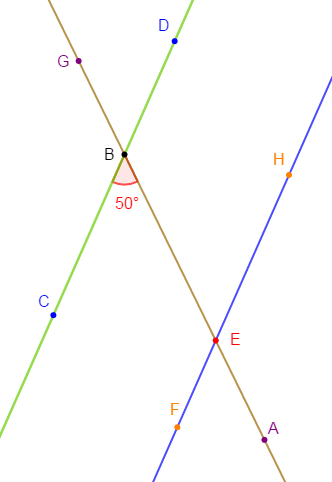
1) Citer deux angles : Alternes internes – Alternes externes - correspondants - opposés par le sommet - intérieurs - extérieurs.
2) Déterminer : $mes\;\widehat{BEH}\ $ et $\ mes\;\widehat{GEF}.$
Exercice 4
On considère la figure ci-dessous.
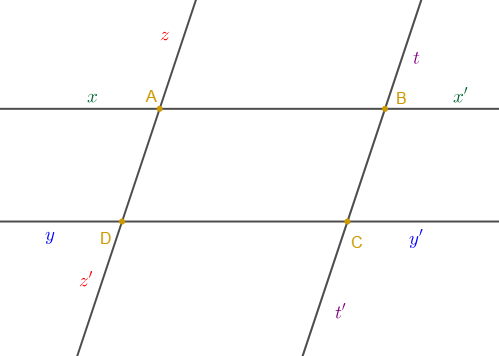
1) Nommer les angles du sommet $A.$
2) Il y a combien d'angle sur la figure ?
3) Citer deux angles : Alternes internes – Alternes externes - correspondants- opposés par le sommet - intérieurs – extérieurs – adjacents supplémentaires.
Exercice 5
1) Trace deux droites $(L)\ $ et $\ (L')$ coupées par une droite sécante $(d_{1})$ qui détermine deux angles alternes internes de $65^{\circ}\ $ et $\ 67^{\circ}.$
2) Les droites sont-elles parallèles ? Justifier.
Exercice 6
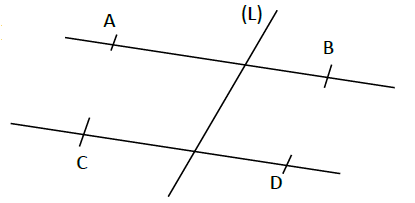
1) Trace deux droites $(L)\ $ et $\ (L')$ coupées par une droite sécante $(d_{1})$ qui détermine deux angles correspondants de $80^{\circ}\ $ et $\ 80^{\circ}.$
2) Les droites sont-elles parallèles ? Justifier.
Exercice 7
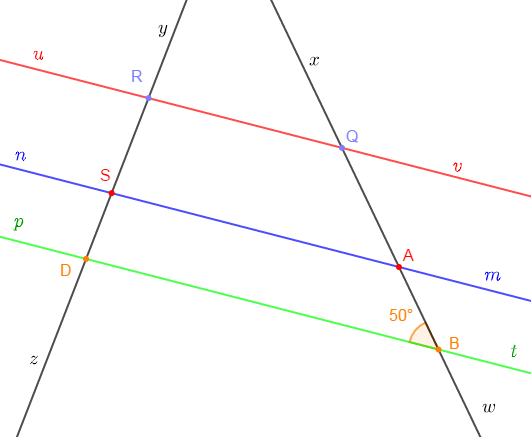
Sur la figure ci-dessous, on donne $\widehat{ABD}=50^{\circ}.$
Sachant que $(RQ)\;;\ (SA)\ $ et $\ (DB)$ sont parallèles entre elles, donne les autres angles de la figure qui mesurent $50^{\circ}.$
Justifie ta réponse.
Exercice 8
La figure suivante a été réalisée à main levée.
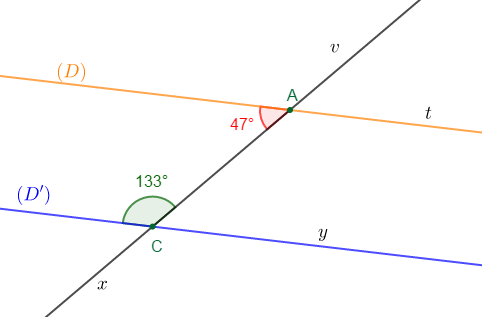
1) Quelle est la mesure de $\widehat{vAt}$ ?
Justifie ta réponse.
2) Donne, en la justifiant, la mesure de $\widehat{vCy}.$
3) Quelle est la mesure de $\widehat{tAx}$ ?
Justifie ta réponse.
4) $(\mathcal{D})\ $ et $\ (\mathcal{D'})$ sont-elle parallèles ?
Pourquoi ?
Exercice 9
Les données de la figure ci-dessous permettent- elles de connaitre la position relative des droites :
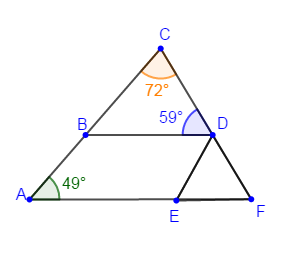
$\centerdot\ \ (AC)\ $ et $\ (ED)$ ?
$\centerdot\ \ (AF)\ $ et $\ (BD)$ ?
Exercice 10
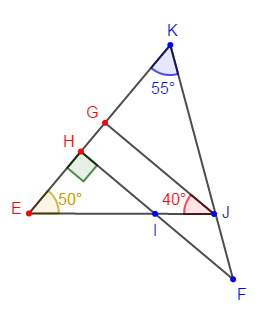
En utilisant la figure ci-dessous :
1) Démontrer que $(GJ)\parallel (FH).$
2) Calcule la mesure en degrés de chacun des angles du triangle $IJF.$
Exercice 11
1) Construis un triangle équilatéral $WAS.$
2) Quelle est la mesure de chacun de ses angles ?
3) Place un point $E$ sur $[WA]$, puis trace la parallèle à $(AS)$ passant par $E$ qui coupe $[WS]$ en $B.$
4) Détermine la mesure des angles du triangle $WEB$, puis précise sa sa nature.
Exercice 12
1) Construis un triangle $ABC$ isocèle en $A$ tel que $\widehat{BAC}=80^{\circ}.$
2) La bissectrice de $\widehat{ABC}$ coupe $[AC]$ en $I$, celle de $\widehat{BIA}$ coupe $[AB]$ en $J$ et la bissectrice de $\widehat{IJA}$ coupe $[AC]$ en $K.$
Place $I\;,\ J\;,\ K.$
3) Calcule tous les angles de la figure.
4) Les droites $(JK)\ $ et $\ (BI)$ sont-elles parallèles ?
Justifie ta réponse.
Exercice 13
1) Trace un rectangle $ABCD$ de centre $O$ et construis $[Ax)\ $ et $\ [Cy)$ symétriques respectives de $(AC)$ par rapport à $(AB)\ $ et $\ (CD).$
2) Quelle est la position relative de $[Ax)\ $ et $\ [Cy)\ ?$
Justifie ta réponse.

Exercice 14
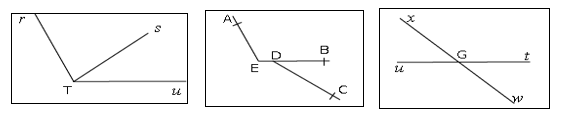
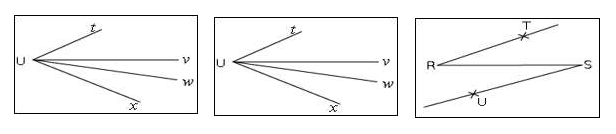
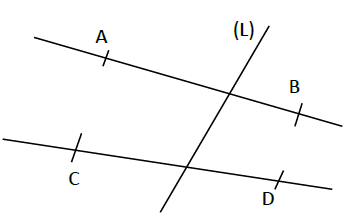
Pour chacune des figures ci-dessous, les angles proposés sont-ils adjacents ? Justifie ta réponse.

a.$\ \widehat{rTs}\ $ et $\ \widehat{sTu}\qquad\quad$ b.$\ \widehat{AEB}\ $ et $\ \widehat{BDC}\qquad\quad$ c.$\ \widehat{xGu}\ $ et $\ \widehat{tGx}$

d.$\ \widehat{vUx}\ $ et $\ \widehat{wUv}\qquad\quad$ e.$\ \widehat{tUv}\ $ et $\ \widehat{wUx}\qquad\quad$ f.$\ \widehat{TRS}\ $ et $\ \widehat{RSU}$
Exercice 15
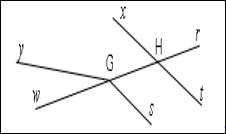
On donne la figure ci-dessous.

Dans chacun des cas ci-dessous, les angles sont-ils opposés par le sommet ?
a) $\widehat{yGw}\ $ et $\ \widehat{HGs}$
b) $\widehat{rHx}\ $ et $\ \widehat{tHw}$
c) $\widehat{rHt}\ $ et $\ \widehat{xHG}\ $
Exercice 16
On donne la figure ci-dessous.

Reproduis puis complète le tableau ci-dessous
$$\begin{array}{|c|c|c|c|c|} \hline \text {Angles}&\widehat{xFr}&\widehat{yFt}&\widehat{sFr}&\widehat{sFw}\\\hline\text{Angles opposés}&&&&\\\text{par le sommet}&&&&\\\hline\end{array}$$
Exercice 17
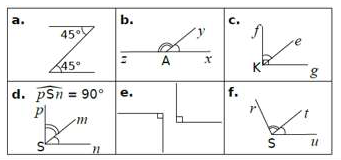
On considère les figures $a\;,\ b\;,\ c\;,\ d\;,\ e\;,\ f$ ci-dessous :

Reproduis et remplis le tableau ci-dessous en mettant une croix dans la ou les cases qui correspondent à des angles adjacents, complémentaires, supplémentaires.
$$\begin{array}{|l|c|c|c|c|c|c|}\hline\text{Angles}\smallsetminus\text{Figures}&a.&b.&c.&d.&e.&f.\\\hline\text{Angles adjacents}&&&&&&\\\hline\text{Angles}&&&&&&\\\text{complémentaires}&&&&&&\\\hline\text{Angles}&&&&&&\\\text{suplémentaires}&&&&&&\\\hline\end{array}$$
Exercice 18
Reproduis et remplis le tableau ci-dessous en mettant une croix dans la case qui convient.
$$\begin{array}{|c|c|c|c|c|}\hline\widehat{a}&\widehat{b}&\text{Complémentaires}&\text{Suplémentaires}&\text{ni l'un, ni l'autre}\\\hline 35^{\circ}&55^{\circ}&&&\\\hline 115&65^{\circ}&&&\\\hline 47^{\circ}&134^{\circ}&&&\\\hline 22^{\circ}&67^{\circ}&&&\\\hline 30^{\circ}&150^{\circ}&&&\\\hline\end{array}$$
Exercice 19
1) Soient $\widehat{a}\ $ et $\ \widehat{b}$ deux angles complémentaires.
Calcule la mesure de l'angle $\widehat{b}$ dans chacun des cas suivants :
$\widehat{a}=57^{\circ}\;;\ \widehat{a}=24^{\circ}\;;\ \widehat{a}=2\widehat{b}$
2) Soient $\widehat{a}\ $ et $\ \widehat{b}$ deux angles supplémentaires.
Calcule la mesure de l'angle $\widehat{b}$ dans chacun des cas suivants :
$\widehat{a}=127^{\circ}\;;\ \widehat{a}=86^{\circ}\;;\ \widehat{a}=3\widehat{b}$
Exercice 20
Reproduis la figure ci-dessous puis colorie différemment les paires d'angles correspondants.

Exercice 21
Reproduis la figure ci-dessous puis colorie différemment les paires d'angles alternes-internes.

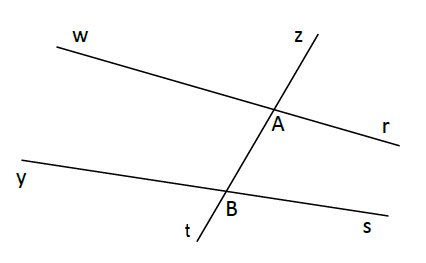
Exercice 22
Recopie puis complète les phrases ci-dessous en t'aidant de la figure ci-dessous :
a) $\widehat{zAr}\ $ et $\ \widehat{zBs}$ sont $\ldots\ldots\ldots$
b) $\widehat{rAt}\ $ et $\ \widehat{yBz}$ sont $\ldots\ldots\ldots$
c) $\widehat{zAr}\ $ et $\ \widehat{zBs}$ sont $\ldots\ldots\ldots$
d) $\widehat{zBs}$ et $\ldots\ldots\ldots$ sont opposés par le sommet.
e) $\widehat{rAt}$ et $\ldots\ldots\ldots$ sont correspondants.
f) $\ldots\ldots\ldots$ et $\widehat{wAB}$ sont alternes-internes.
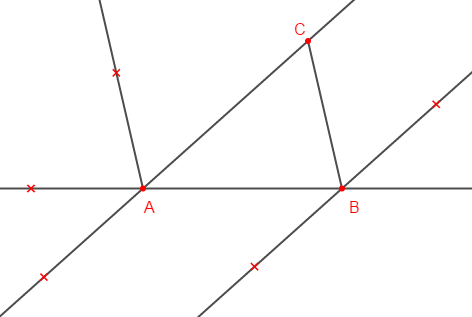
Exercice 23
On donne la figure ci-dessous
Reproduis la figure ci-dessus en plaçant les points $D\;,\ E\;,\ F\;,\ G\ $ et $\ H$ sachant que :
$\centerdot\ \ $ les angles $\widehat{BAC}\ $ et $\ \widehat{ABD}$ sont alternes-internes;
$\centerdot\ \ $ les angles $\widehat{CAB}\ $ et $\ \widehat{BAE}$ sont supplémentaires;
$\centerdot\ \ $ les angles $\widehat{CAB}\ $ et $\ \widehat{EAF}$ sont des angles opposés par le sommet;
$\centerdot\ \ $ les angles $\widehat{ABC}\ $ et $\ \widehat{FAG}$ sont correspondants;
$\centerdot\ \ $ les angles $\widehat{ACB}\ $ et $\ \widehat{CBH}$ sont alternes-internes.

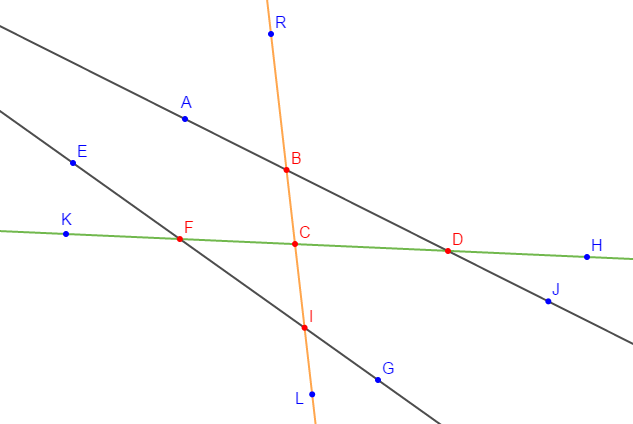
Exercice 24
On considère la figure ci-dessous.

Cite deux paires d'angles :
1) correspondants déterminés par les droites $(EG)\;,\ (AD)$ et la sécante $(KC)$ ;
2) alternes-internes déterminés par les droites $(EG)\;,\ (AD)$ et la sécante $(BR)$ ;
3) alternes-externes déterminés par les droites $(EG)\;,\ (AD)$ et la sécante $(BR)$ ;
4) opposés par le sommet.
Exercice 25
1) Reproduis la figure ci-contre puis colorie avec la même couleur les angles de même mesure sachant que les droites $(AB)\ $ et $\ (CD)$ ne sont pas parallèles.

2) Reproduis la figure ci-contre puis colorie avec la même couleur les angles de même mesure sachant que les droites $(AB)\ $ et $\ (CD)$ sont parallèles.

Exercice 26
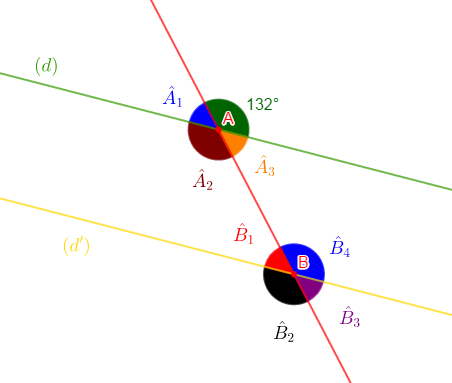
Dans la figure ci-dessous, les droites $(d)\ $ et $\ (d')$ sont parallèles.
Donne la mesure de chacun des angles
$\widehat{A}_{1}\;;\ \widehat{A}_{2}\;;\ \widehat{A}_{2}\;;\ \widehat{B}_{1}\;;\ \widehat{B}_{2}\;;\ \widehat{B}_{3}\ $ et $\ \widehat{B}_{4}.$ Justifie.

Exercice 27
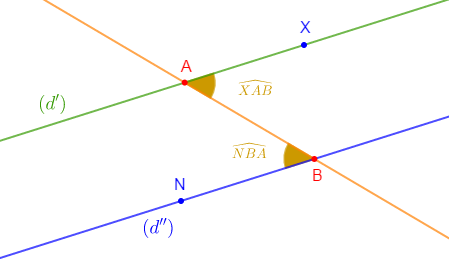
Dans la figure ci-dessous, les droites $(d')\ $ et $\ (d'')$ sont parallèles. Démontre que les angles $\widehat{XAB}\ $ et $\ \widehat{NBA}$ ont la même mesure.

Exercice 28
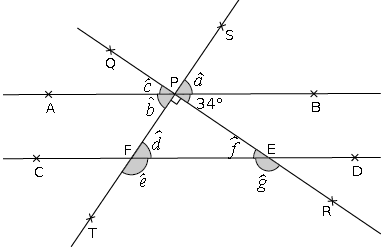
Sachant que dans cette figure les droites $(AB)\ $ et $\ (CD)$ sont parallèles, donne la mesure de chacun des angles ci-dessous sans mesurer : $\widehat{a}\;;\ \widehat{b}\;;\ \widehat{c}\;;\ \widehat{d}\;;\ \widehat{e}\;;\ \widehat{f}\ $ et $\ \widehat{g}.$

Exercice 29
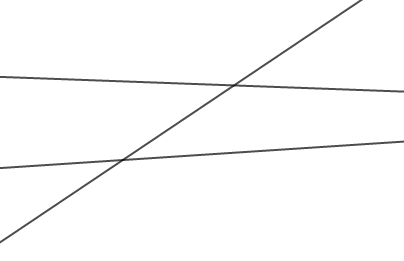
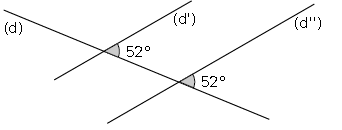
Dans la figure ci-dessous, les droites $(d')\ $ et $\ (d'')$ sont-elles parallèles ? Justifie ta réponse.

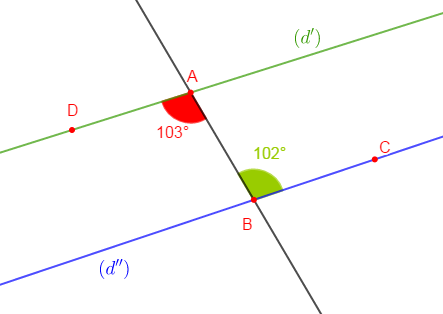
Exercice 30
Dans la figure ci-dessous, $\widehat{DAB}=103^{\circ}\ $ et $\ \widehat{CBA}=102^{\circ}.$ Les droites $(d')\ $ et $\ (d'')$ sont-elles parallèles ?
Justifie ta réponse.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Anonyme (non vérifié)
sam, 07/06/2019 - 16:15
Permalien
Bien
Anonyme (non vérifié)
jeu, 03/19/2020 - 08:59
Permalien
Sunudaara est vraiment très
Anonyme (non vérifié)
lun, 10/18/2021 - 12:46
Permalien
Pdf
Anonyme (non vérifié)
lun, 01/02/2023 - 23:08
Permalien
Exercice 19 20 et 21
Moustapha Dieng (non vérifié)
mer, 01/25/2023 - 21:43
Permalien
Exercice
Moustapha Dieng (non vérifié)
mer, 01/25/2023 - 21:43
Permalien
Exercice
Camara (non vérifié)
jeu, 01/26/2023 - 13:53
Permalien
C'est quoi des angles
Anonyme (non vérifié)
dim, 02/05/2023 - 20:03
Permalien
Ou est correction de exercice
Ndiaye (non vérifié)
dim, 02/05/2023 - 20:06
Permalien
Réussir
Ndiaye (non vérifié)
dim, 02/05/2023 - 20:16
Permalien
Exercice 22
Anonyme (non vérifié)
dim, 11/26/2023 - 20:59
Permalien
excellent
Ngary dione (non vérifié)
jeu, 03/06/2025 - 17:31
Permalien
Félicitations
Boubacar Ba (non vérifié)
mer, 03/19/2025 - 15:58
Permalien
Formidable
Ajouter un commentaire