Solution des exercices : Les angles - 5e
Classe:
Cinquième
Exercice 1
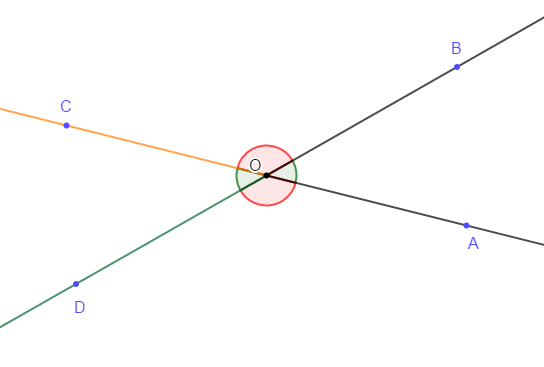
Soit $AOB$ un angle aigu.
1) Construisons le point $C$ symétrique de $A$ par rapport au sommet $O.$
2) Construisons le point $D$ symétrique de $B$ par rapport au sommet $O.$
3) $[OC)$ est le symétrique de $[OA)$ par rapport à $O.$ Par suite, $[OA)\ $ et $\ [OC)$ sont de même direction et de sens opposés.
De même, $[OD)$ étant le symétrique de $[OB)$ par rapport à $O$ alors, $[OB)\ $ et $\ [OD)$ sont de même direction et de sens opposés.
4) L'angle $COD$ étant l'image de l'angle $AOB$ par la symétrie centrale de centre $O$ alors, $\widehat{AOB}\ $ et $\ \widehat{COD}$ ont la même mesure.
Par ailleurs, les angles $COB\ $ et $\ AOD$ étant opposés par le sommet $O$ donc, sont de même mesure.
Ainsi,
$$mes\,\widehat{AOB}=mes\,\widehat{COD}\quad\text{et}\quad mes\,\widehat{COB}=mes\,\widehat{AOD}$$
Exercice 2
On considère la figure ci-dessous tel que $mes\;\widehat{x'Oy}=60^{\circ}.$
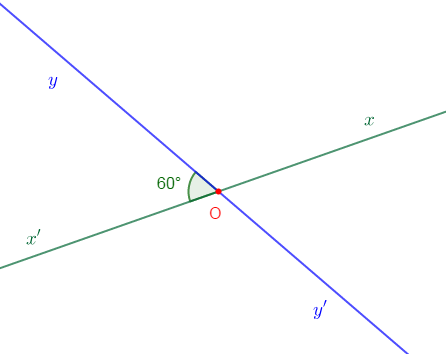
Déterminons :
$mes\;\widehat{xOy'}\;;\ mes\;\widehat{xOy}\ $ et $\ mes\;\widehat{x'Oy'}$
Les angles $\widehat{xOy'}\ $ et $\ \widehat{x'Oy}$ étant opposés par le sommet $O$ alors, ils sont égaux.
Donc, $mes\;\widehat{xOy'}=mes\;\widehat{x'Oy}=60^{\circ}$
D'où, $\boxed{mes\;\widehat{xOy'}=60^{\circ}}$
On a : $\widehat{xOy}\ $ et $\ \widehat{x'Oy}$ sont deux angles adjacents supplémentaires donc, $mes\;\widehat{xOy}+mes\;\widehat{x'Oy}=180^{\circ}$
Par suite, $mes\;\widehat{xOy}=180^{\circ}-mes\;\widehat{x'Oy}$
Or, $\ mes\;\widehat{x'Oy}=60^{\circ}$
Donc, $mes\;\widehat{xOy}=180^{\circ}-60^{\circ}=120^{\circ}$
Ainsi, $\boxed{mes\;\widehat{xOy}=120^{\circ}}$
Comme les angles $\widehat{x'Oy'}\ $ et $\ \widehat{xOy}$ sont opposés par le sommet $O$ alors, ils sont égaux.
Ce qui peut s'écrire, $mes\;\widehat{x'Oy'}=mes\;\widehat{xOy}$
Or, $mes\;\widehat{xOy}=120^{\circ}$
Par conséquent, $\boxed{mes\;\widehat{x'Oy'}=120^{\circ}}$
Exercice 3
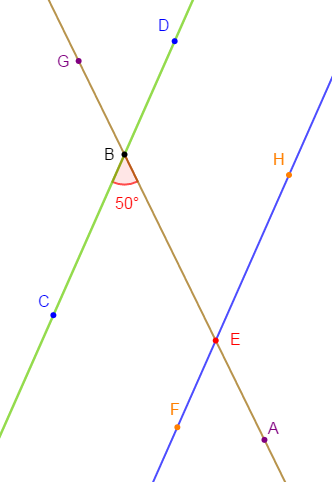
On considère la figure ci-dessous : $(DC)\ $ et $\ (HF)$ sont parallèles. La droite $(AG)$ coupe $(DC)$ en $B\ $ et $\ (HF)$ en $E$ tel que $mes\;\widehat{ABC}=50^{\circ}.$

1) Citons deux angles : Alternes internes – Alternes externes - correspondants - opposés par le sommet - intérieurs - extérieurs.
On a :
$\widehat{ABC}\ $ et $\ \widehat{BEH}$ sont deux angles alternes-internes.
$\widehat{CBG}\ $ et $\ \widehat{AEH}$ sont deux angles alternes-externes.
$\widehat{DBE}\ $ et $\ \widehat{AEH}$ sont deux angles correspondants.
$\widehat{AEF}\ $ et $\ \widehat{BEH}$ sont deux angles opposés par le sommet $E.$
$\widehat{DBE}\ $ et $\ \widehat{BEH}$ sont deux angles intérieurs à la bande délimitée par les deux droites parallèles $(DC)\ $ et $\ (HF).$
$\widehat{DBG}\ $ et $\ \widehat{AEH}$ sont deux angles extérieurs à la bande délimitée par les deux droites parallèles $(DC)\ $ et $\ (HF).$
2) Déterminons : $mes\;\widehat{BEH}\ $ et $\ mes\;\widehat{GEF}.$
On a : $\widehat{ABC}\ $ et $\ \widehat{BEH}$ sont deux angles alternes-internes.
Or, on sait que : deux droites parallèles coupées par une sécante déterminent deux angles alternes internes de même mesure.
Comme $(DC)\ $ et $\ (HF)$ sont deux droites parallèles coupées par la droite sécante $(AG)$ alors, les angles $\widehat{ABC}\ $ et $\ \widehat{BEH}$ sont de même mesure.
Ce qui signifie que : $mes\;\widehat{BEH}=mes\;\widehat{ABC}=50^{\circ}$
D'où, $\boxed{mes\;\widehat{BEH}=50^{\circ}}$
On a : les angles $\widehat{GEF}\ $ et $\ \widehat{BEH}$ sont adjacents supplémentaires.
Donc, $mes\;\widehat{GEF}+mes\;\widehat{BEH}=180^{\circ}$
Ce qui entraine alors : $mes\;\widehat{GEF}=180^{\circ}-mes\;\widehat{BEH}$
En remplaçant $mes\;\widehat{BEH}$ par sa valeur, on obtient :
$\begin{array}{rcl}mes\;\widehat{GEF}&=&180^{\circ}-mes\;\widehat{BEH}\\\\&=&180^{\circ}-50^{\circ}\\\\&=&130^{\circ}\end{array}$
Ainsi, $\boxed{mes\;\widehat{GEF}=130^{\circ}}$
Exercice 4
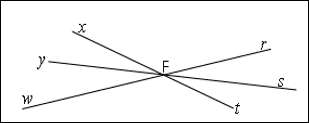
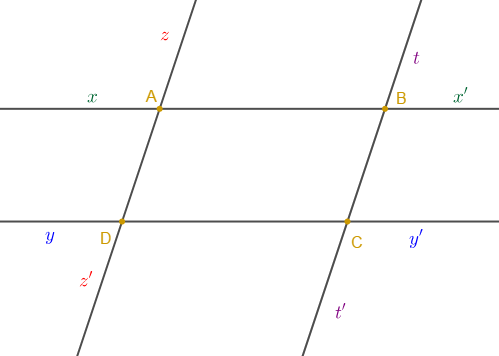
On considère la figure ci-dessous.

1) Nommons les angles du sommet $A.$
On peut citer :
$$\widehat{xAz}\;;\ \widehat{xAz'}\;;\ \widehat{z'Ax'}\;;\ \widehat{zAx'}\;;\ \widehat{xAx'}\;;\ \widehat{zAz'}$$
2) Sur la figure on peut compter $24$ angles.
Au niveau de chaque sommet, on a $6$ angles. Donc, pour les $4$ sommets on obtient : $4\times 6=24$ angles.
D'où, on peut compter $24$ angles sur la figure.
3) Citons deux angles : Alternes internes - Alternes externes - correspondants - opposés par le sommet - intérieurs - extérieurs - adjacents supplémentaires.
On a :
$\widehat{x'Bt'}\ $ et $\ \widehat{yCt}$ sont deux angles alternes-internes.
$\widehat{xAz}\ $ et $\ \widehat{z'Dy'}$ sont deux angles alternes-externes.
$\widehat{zAx'}\ $ et $\ \widehat{zDy'}$ sont deux angles correspondants.
$\widehat{tCy'}\ $ et $\ \widehat{yCt'}$ sont deux angles opposés par le sommet $C.$
$\widehat{ABC}\ $ et $\ \widehat{ADC}$ sont deux angles intérieurs au quadrilatère $ABCD.$
$\widehat{xAz}\ $ et $\ \widehat{yDz'}$ sont deux angles extérieurs au quadrilatère $ABCD.$
$\widehat{xAz}\ $ et $\ \widehat{zAx'}$ sont deux angles adjacents supplémentaires.
Exercice 5
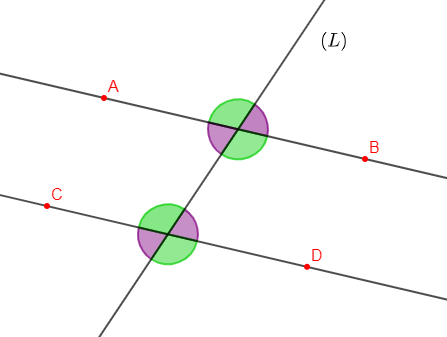
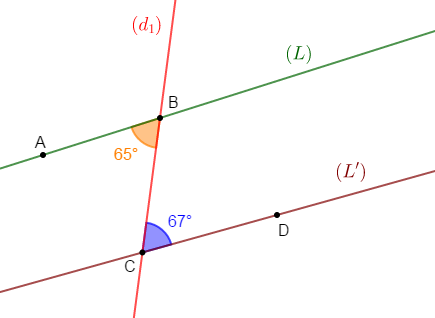
1) Traçons deux droites $(L)\ $ et $\ (L')$ coupées par une droite sécante $(d_{1})$ qui détermine deux angles alternes internes de $65^{\circ}\ $ et $\ 67^{\circ}.$
2) Les droites $(L)\ $ et $\ (L')$ ne sont pas parallèles
Justifions :
En effet, on sait que : si deux angles alternes internes déterminés par deux droites et une sécante ne sont pas de même mesure alors, les deux droites ne sont pas parallèles.
Or, on constate que les angles alternes internes $\widehat{ABC}\ $ et $\ \widehat{BCD}$ ne sont pas de même mesure.
Donc, d'après la propriété, les droites $(L)\ $ et $\ (L')$ ne sont pas parallèles.

Exercice 6
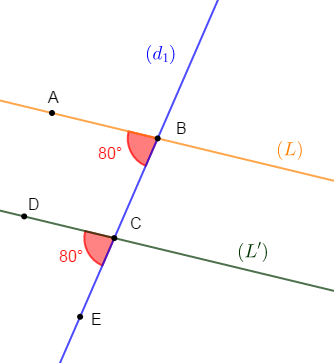
1) Traçons deux droites $(L)\ $ et $\ (L')$ coupées par une droite sécante $(d_{1})$ qui détermine deux angles correspondants de $80^{\circ}\ $ et $\ 80^{\circ}.$
2) Les droites $(L)\ $ et $\ (L')$ sont parallèles
Justifions :
En effet, on sait que : si deux angles correspondants déterminés par deux droites et une sécante sont de même mesure alors, les deux droites sont parallèles.
Or, on remarque que les angles correspondants $\widehat{ABC}\ $ et $\ \widehat{DCE}$ ont la même mesure de $80^{\circ}.$
Par conséquent, les droites $(L)\ $ et $\ (L')$ qui les déterminent sont parallèles.

Exercice 7
Sur la figure ci-dessous, on donne $\widehat{ABD}=50^{\circ}.$
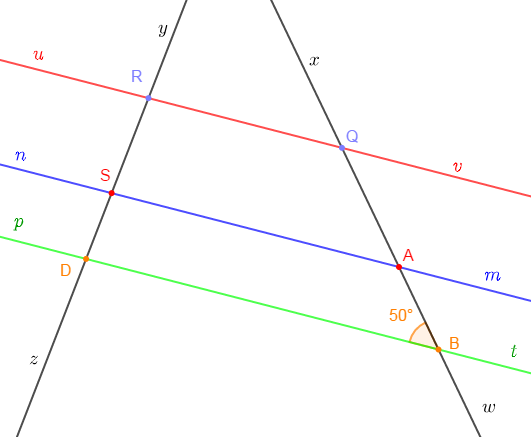
Sachant que $(RQ)\;;\ (SA)\ $ et $\ (DB)$ sont parallèles entre elles, donnons les autres angles de la figure qui mesurent $50^{\circ}.$
Les autres angles de la figure qui mesurent $50^{\circ}$ sont :
$$\widehat{QAS}\;;\ \widehat{xQR}\;;\ \widehat{tBw}\;;\ \widehat{mAB}\;;\ \widehat{vQA}$$
Justifie ta réponse.
On sait que : deux droites parallèles coupées par une droite sécante déterminent deux angles correspondants de même mesure.
Comme les droites $(SA)\ $ et $\ (DB)$ sont parallèles et sont coupées par la droite sécante $(BQ)$ alors, les angles correspondants $\widehat{ABD}\ $ et $\ \widehat{QAS}$ sont de même mesure.
Ce qui signifie que : $\widehat{QAS}=\widehat{ABD}$
D'où, $\boxed{\widehat{QAS}=50^{\circ}}$
On a aussi : les droites $(RQ)\ $ et $\ (DB)$ sont parallèles et sont coupées par la droite sécante $(BQ)$ donc, les angles correspondants $\widehat{ABD}\ $ et $\ \widehat{xQR}$ sont de même mesure.
Ce qui signifie alors : $\widehat{xQR}=\widehat{ABD}$
Ainsi, $\boxed{\widehat{xQR}=50^{\circ}}$
Par ailleurs, on remarque que $\widehat{ABD}\ $ et $\ \widehat{tBw}$ sont deux angles opposés par le sommet $B.$
Donc, ils sont de même mesure.
Ce qui signifie que : $\widehat{tBw}=\widehat{ABD}$
D'où, $\boxed{\widehat{tBw}=50^{\circ}}$
De même, on constate que $\widehat{QAS}\ $ et $\ \widehat{mAB}$ sont deux angles opposés par le sommet $A.$
Ils ont alors la même mesure.
Donc, $\widehat{mAB}=\widehat{QAS}$
Ainsi, $\boxed{\widehat{mAB}=50^{\circ}}$
On a aussi : $\widehat{xQR}\ $ et $\ \widehat{vQA}$ sont deux angles opposés par le sommet $Q.$
Donc, ils ont la même mesure.
Ce qui signifie que : $\widehat{vQA}=\widehat{xQR}$
D'où, $\boxed{\widehat{vQA}=50^{\circ}}$

Exercice 8
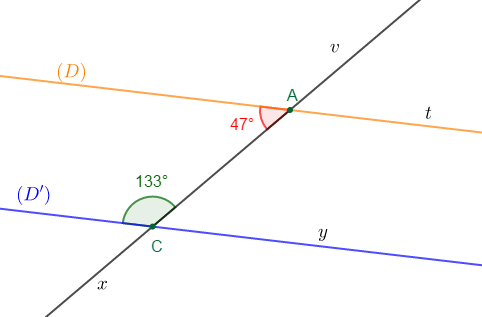
La figure suivante a été réalisée à main levée.

1) La mesure de $\widehat{vAt}$ est de $47^{\circ}$
Justifions notre réponse.
On a : $\widehat{vAt}\ $ et l'angle de $47^{\circ}$ sont opposés par le sommet $A.$
Or, on sait que deux angles opposés par le sommet sont de même mesure.
Par conséquent, $\boxed{\widehat{vAt}=47^{\circ}}$
2) Donnons, en la justifiant, la mesure de $\widehat{vCy}.$
On a : $\widehat{vCy}\ $ et l'angle de $133^{\circ}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{vCy}+133^{\circ}=180^{\circ}$
Ce qui entraine alors : $\widehat{vCy}=180^{\circ}-133^{\circ}=47^{\circ}$
D'où, $\boxed{mes\;\widehat{vCy}=47^{\circ}}$
3) La mesure de $\widehat{tAx}$ est égale à $133^{\circ}$
Justifions notre réponse.
On a : les angles $\widehat{vAt}\ $ et $\ \widehat{tAx}$ sont adjacents supplémentaires.
Donc, $mes\;\widehat{tAx}+mes\;\widehat{vAt}=180^{\circ}$
Ce qui entraine alors : $mes\;\widehat{tAx}=180^{\circ}-mes\;\widehat{vAt}$
En remplaçant $mes\;\widehat{vAt}$ par sa valeur, on obtient :
$\begin{array}{rcl}mes\;\widehat{tAx}&=&180^{\circ}-mes\;\widehat{vAt}\\\\&=&180^{\circ}-47^{\circ}\\\\&=&133^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{tAx}=133^{\circ}}$
4) Les droites $(\mathcal{D})\ $ et $\ (\mathcal{D'})$ sont bien parallèles.
En effet, on sait que : si deux droites coupées par une sécante déterminent deux angles correspondants de même mesure alors, ces deux droites sont parallèles.
Or, on remarque que les droites $(\mathcal{D})\ $ et $\ (\mathcal{D'})$ coupées par la droite sécante $(AC)$ déterminent deux angles correspondants $\widehat{vAt}\ $ et $\ \widehat{vCy}$ qui ont la même mesure de $47^{\circ}.$
Par conséquent, les droites $(\mathcal{D})\ $ et $\ (\mathcal{D'})$ sont parallèles.
Exercice 9
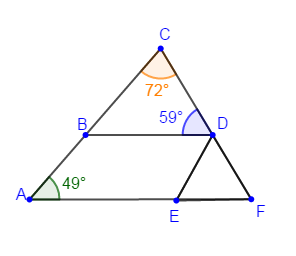
On considère la figure ci-dessous

Alors, les données de la figure ne permettent pas de connaitre la position relative des droites $(AC)\ $ et $\ (ED).$
En effet, les données de la figure ne permettent pas de faire la comparaison des angles alternes-internes, alternes-externes ou correspondants déterminés par les droites $(AC)\ $ et $\ (ED).$
Par conséquent, on ne peut rien dire sur la position relative de ces deux droites.
Par contre, les données de la figure permettent de connaitre la position relative des droites $(AF)\ $ et $\ (BD).$
En calculant la mesure de l'angle $\widehat{CBD}$ et en comparant les angles correspondants $\widehat{CBD}\ $ et $\ \widehat{BAF}$, on peut connaitre la position relative des droites $(AF)\ $ et $\ (BD).$
Calculons alors la mesure de l'angle $\widehat{CBD}$
Comme la somme des angles d'un triangle est égale à $180^{\circ}$ alors, pour le triangle $BCD$ on a :
$$\widehat{CBD}+\widehat{BDC}+\widehat{BCD}=180^{\circ}$$
Ce qui entraine alors : $\widehat{CBD}=180^{\circ}-(\widehat{BDC}+\widehat{BCD})$
En remplaçant $\widehat{BDC}\ $ et $\ \widehat{BCD}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{CBD}&=&180^{\circ}-(\widehat{BDC}+\widehat{BCD})\\\\&=&180^{\circ}-(59^{\circ}+72^{\circ})\\\\&=&180^{\circ}-131^{\circ}\\\\&=&49^{\circ}\end{array}$
Donc, $\boxed{\widehat{CBD}=49^{\circ}}$
On remarque alors que $\widehat{CBD}\ $ et $\ \widehat{BAF}$ ont la même mesure de $49^{\circ}.$
Ainsi, les droites $(AF)\ $ et $\ (BD)$ coupées par la sécante $(AC)$, déterminent deux angles correspondants, $\widehat{CBD}\ $ et $\ \widehat{BAF}$, de même mesure $49^{\circ}.$
Par conséquent, les droites $(AF)\ $ et $\ (BD)$ sont parallèles.
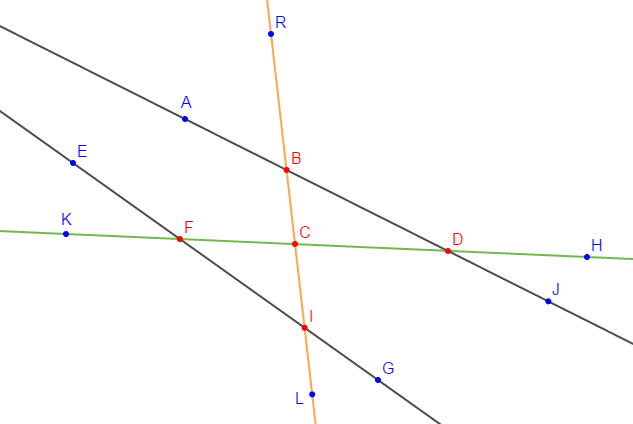
Exercice 10
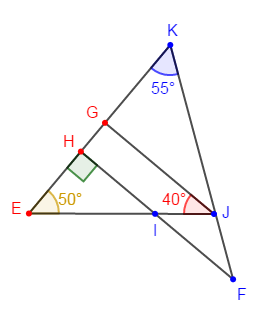
En utilisant la figure ci-dessous :
1) Démontrer que $(GJ)$ est parallèle à $(FH).$
Pour cela, on va montrer que les angles alternes-internes $\widehat{GJI}\ $ et $\ \widehat{JIF}$ ont la même mesure.
Calculons alors la mesure de l'angle $\widehat{JIF}.$
On sait que $\widehat{JIF}\ $ et $\ \widehat{HIE}$ sont deux angles opposés par le sommet $I$ donc, ils sont de même mesure.
C'est-à-dire ; $mes\;\widehat{JIF}=mes\;\widehat{HIE}$
Or, la mesure de l'angle $\widehat{HIE}$ est obtenue la propriété sur la somme des angles d'un triangle.
Considérons alors le triangle $HIE.$
Comme la somme des angles d'un triangle est égale à $180^{\circ}$ alors, on a :
$$\widehat{HIE}+\widehat{HEI}+\widehat{IHE}=180^{\circ}$$
Ce qui entraine : $\widehat{HIE}=180^{\circ}-(\widehat{HEI}+\widehat{IHE})$
En remplaçant $\widehat{HEI}\ $ et $\ \widehat{IHE}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{HIE}&=&180^{\circ}-(\widehat{HEI}+\widehat{IHE})\\\\&=&180^{\circ}-(50^{\circ}+90^{\circ})\\\\&=&180^{\circ}-140^{\circ}\\\\&=&40^{\circ}\end{array}$
Donc, $mes\;\widehat{HIE}=40^{\circ}$
Par suite, $\boxed{mes\;\widehat{JIF}=40^{\circ}}$
On remarque alors que les angles $\widehat{GJI}\ $ et $\ \widehat{JIF}$ ont la même mesure de $40^{\circ}.$
Ainsi, les droites $(GJ)\ $ et $\ (FH)$ coupées par la sécante $(EJ)$, déterminent deux angles alternes-internes, $\widehat{GJI}\ $ et $\ \widehat{JIF}$, de même mesure $40^{\circ}.$
Par conséquent, les droites $(GJ)\ $ et $\ (FH)$ sont parallèles.
2) Calculons la mesure en degrés de chacun des angles du triangle $IJF.$
On constate que les angles $\widehat{IJF}\ $ et $\ \widehat{EJK}$ sont adjacents supplémentaires.
Pour cela, on calcule d'abord la mesure de l'angle $\widehat{EJK}$ ensuite, on tire la mesure de l'angle $\widehat{IJF}$ car ces deux angles sont adjacents supplémentaires.
En considérant le triangle $EJK$, on a :
$$\widehat{EJK}+\widehat{EKJ}+\widehat{JEK}=180^{\circ}$$
Ce qui entraine alors : $\widehat{EJK}=180^{\circ}-(\widehat{EKJ}+\widehat{JEK})$
En remplaçant $\widehat{EKJ}\ $ et $\ \widehat{JEK}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{EJK}&=&180^{\circ}-(\widehat{EKJ}+\widehat{JEK})\\\\&=&180^{\circ}-(55^{\circ}+50^{\circ})\\\\&=&180^{\circ}-105^{\circ}\\\\&=&75^{\circ}\end{array}$
Donc, $mes\;\widehat{EJK}=75^{\circ}$
Comme les angles $\widehat{IJF}\ $ et $\ \widehat{EJK}$ sont adjacents supplémentaires alors, cela signifie que : $\widehat{IJF}+\widehat{EJK}=180^{\circ}$
Ce qui entraine alors : $\widehat{IJF}=180^{\circ}-\widehat{EJK}$
En remplaçant $\widehat{EJK}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{IJF}&=&180^{\circ}-\widehat{EJK}\\\\&=&180^{\circ}-75^{\circ}\\\\&=&105^{\circ}\end{array}$
Ainsi, $\boxed{mes\;\widehat{IJF}=105^{\circ}}$
Par ailleurs, on sait que la somme des angles d'un triangle est égale à $180^{\circ}.$
Donc, en considérant le triangle $IJF$, on obtient :
$$\widehat{IFJ}+\widehat{IJF}+\widehat{JIF}=180^{\circ}$$
Ce qui entraine : $\widehat{IFJ}=180^{\circ}-(\widehat{IJF}+\widehat{JIF})$
En remplaçant $\widehat{IJF}\ $ et $\ \widehat{JIF}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{IFJ}&=&180^{\circ}-(\widehat{IJF}+\widehat{JIF})\\\\&=&180^{\circ}-(105^{\circ}+40^{\circ})\\\\&=&180^{\circ}-145^{\circ}\\\\&=&35^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{IFJ}=35^{\circ}}$

Exercice 11
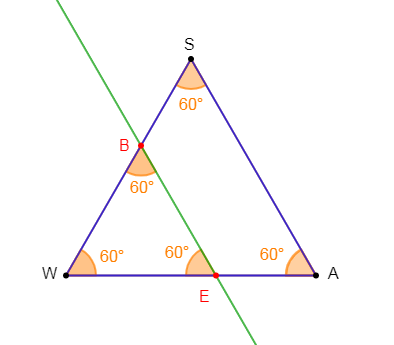
1) Construisons un triangle équilatéral $WAS.$
2) La mesure de chacun de ses angles est égale à $60^{\circ}.$
En effet, $WAS$ est un triangle équilatéral.
Or, un triangle équilatéral a trois angles internes qui ont la même mesure de $60^{\circ}.$
Donc, chaque angle de $WAS$ mesure $60^{\circ}$
3) Plaçons un point $E$ sur $[WA]$, puis traçons la parallèle à $(AS)$ passant par $E$ qui coupe $[WS]$ en $B.$
4) Déterminons la mesure des angles du triangle $WEB$, puis précisons sa sa nature.
On a : les deux droites parallèles $(BE)\ $ et $\ (AS)$ coupées par la droite sécante $(WS)$, déterminent deux angles correspondants $\widehat{WBE}\ $ et $\ \widehat{WSA}$ de même mesure.
Ce qui signifie que : $\widehat{WBE}\widehat{WSA}$
Or, $\widehat{WSA}=60^{\circ}$
Donc, $\boxed{mes\;\widehat{WBE}=60^{\circ}}$
De la même manière, les deux droites parallèles $(BE)\ $ et $\ (AS)$ coupées par la droite sécante $(WA)$, déterminent deux angles correspondants $\widehat{WEB}\ $ et $\ \widehat{WAS}$ de même mesure.
Ce qui donne alors : $\widehat{WEB}=\widehat{WAS}$
Or, $\widehat{WAS}=60^{\circ}$
Donc, $\boxed{mes\;\widehat{WEB}=60^{\circ}}$
On remarque que les trois angles du triangle $WEB$ ont la même mesure de $60^{\circ}.$
Par conséquent, $WEB$ est un triangle équilatéral.

Exercice 12
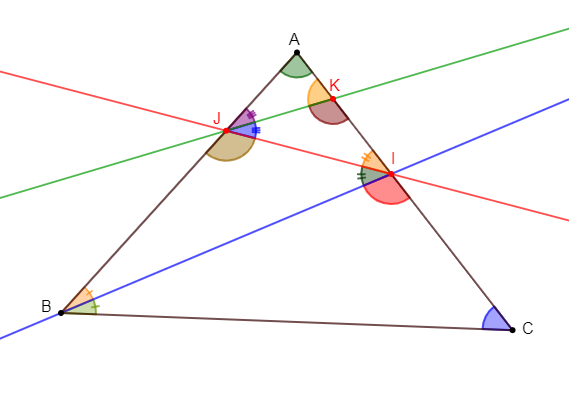
1) Construisons un triangle $ABC$ isocèle en $A$ tel que $\widehat{BAC}=80^{\circ}.$
2) La bissectrice de $\widehat{ABC}$ coupe $[AC]$ en $I$, celle de $\widehat{BIA}$ coupe $[AB]$ en $J$ et la bissectrice de $\widehat{IJA}$ coupe $[AC]$ en $K.$
Plaçons $I\;,\ J\;,\ K.$
3) Calculons tous les angles de la figure.
$-\ $ Calcul de $\widehat{ABC}\ $ et $\ \widehat{ACB}$
En effet, comme le triangle $ABC$ est isocèle en $A$ alors, les angles $\widehat{ABC}\ $ et $\ \widehat{ACB}$ sont de même mesure.
Donc, en considérant le triangle $ABC$, on a :
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^{\circ}$
Ce qui entraine : $\widehat{ABC}+\widehat{ACB}=180^{\circ}-\widehat{BAC}$
En remplaçant $\widehat{BAC}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{ABC}+\widehat{ACB}&=&180^{\circ}-\widehat{BAC}\\\\&=&180^{\circ}-80^{\circ}\\\\&=&100^{\circ}\end{array}$
Or, on sait que : $\widehat{ABC}=\widehat{ACB}$
Par suite, $\widehat{ABC}=\widehat{ACB}=\dfrac{100^{\circ}}{2}=50^{\circ}$
D'où, $\boxed{\widehat{ABC}=\widehat{ACB}=50^{\circ}}$
$-\ $ Calcul de $\widehat{ABI}\ $ et $\ \widehat{IBC}$
Comme la bissectrice d'un angle partage l'angle en deux angles de même mesure alors, les angles adjacents $\widehat{ABI}\ $ et $\ \widehat{IBC}$ ont la même mesure.
Ce qui signifie que : $\widehat{ABI}=\widehat{IBC}=\dfrac{50^{\circ}}{2}=25^{\circ}$
Ainsi, $\boxed{\widehat{ABI}=\widehat{IBC}=25^{\circ}}$
$-\ $ Calcul de $\widehat{BIC}$
En considérant le triangle $BIC$, on a :
$$\widehat{BIC}+\widehat{IBC}+\widehat{ACB}=180^{\circ}$$
Ce qui entraine : $\widehat{BIC}=180^{\circ}-(\widehat{IBC}+\widehat{ACB})$
En remplaçant $\widehat{IBC}\ $ et $\ \widehat{ACB}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{BIC}&=&180^{\circ}-(\widehat{IBC}+\widehat{ACB})\\\\&=&180^{\circ}-(25^{\circ}+50^{\circ})\\\\&=&180^{\circ}-75^{\circ}\\\\&=&105^{\circ}\end{array}$
D'où, $\boxed{\widehat{BIC}=105^{\circ}}$
$-\ $ Calcul de $\widehat{BIA}$
On a : $\widehat{BIA}\ $ et $\ \widehat{BIC}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{BIA}+\widehat{BIC}=180^{\circ}$
Ce qui entraine alors : $\widehat{BIA}=180^{\circ}-\widehat{BIC}$
En remplaçant $\widehat{BIC}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{BIA}&=&180^{\circ}-\widehat{BIC}\\\\&=&180^{\circ}-105^{\circ}\\\\&=&75^{\circ}\end{array}$
D'où, $\boxed{\widehat{BIA}=75^{\circ}}$
$-\ $ Calcul de $\widehat{BIJ}\ $ et $\ \widehat{AIJ}$
Comme $(IJ)$ est la bissectrice de l'angle $\widehat{BIA}$ alors, les angles adjacents $\widehat{BIJ}\ $ et $\ \widehat{AIJ}$ sont de même mesure.
Alors, $\widehat{BIJ}=\widehat{AIJ}=\dfrac{75^{\circ}}{2}=37.5^{\circ}$
Ainsi, $\boxed{\widehat{BIJ}=\widehat{AIJ}=37.5^{\circ}}$
$-\ $ Calcul de $\widehat{BJI}$
En considérant le triangle $BIJ$, on a :
$$\widehat{BJI}+\widehat{BIJ}+\widehat{JBI}=180^{\circ}$$
Ce qui entraine : $\widehat{BJI}=180^{\circ}-(\widehat{BIJ}+\widehat{JBI})$
En remplaçant $\widehat{BIJ}\ $ et $\ \widehat{JBI}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{BJI}&=&180^{\circ}-(\widehat{BIJ}+\widehat{JBI})\\\\&=&180^{\circ}-(37.5^{\circ}+25^{\circ})\\\\&=&180^{\circ}-62.5^{\circ}\\\\&=&117.5^{\circ}\end{array}$
D'où, $\boxed{\widehat{BJI}=117.5^{\circ}}$
$-\ $ Calcul de $\widehat{IJA}$
On a : $\widehat{IJA}\ $ et $\ \widehat{BJI}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{IJA}+\widehat{BJI}=180^{\circ}$
Ce qui entraine alors : $\widehat{IJA}=180^{\circ}-\widehat{BJI}$
En remplaçant $\widehat{BJI}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{IJA}&=&180^{\circ}-\widehat{BJI}\\\\&=&180^{\circ}-117.5^{\circ}\\\\&=&62.5^{\circ}\end{array}$
D'où, $\boxed{\widehat{IJA}=62.5^{\circ}}$
$-\ $ Calcul de $\widehat{IJK}\ $ et $\ \widehat{AJK}$
Comme $(JK)$ est la bissectrice de l'angle $\widehat{IJA}$ alors, les angles adjacents $\widehat{IJK}\ $ et $\ \widehat{AJK}$ ont la même mesure.
Donc, $\widehat{IJK}=\widehat{AJK}=\dfrac{62.5^{\circ}}{2}=31.25^{\circ}$
D'où, $\boxed{\widehat{IJK}=\widehat{AJK}=31.25^{\circ}}$
$-\ $ Calcul de $\widehat{JKI}$
En considérant le triangle $IJK$, on a :
$$\widehat{JKI}+\widehat{IJK}+\widehat{KIA}=180^{\circ}$$
Ce qui entraine : $\widehat{JKI}=180^{\circ}-(\widehat{IJK}+\widehat{KIJ})$
En remplaçant $\widehat{IJK}\ $ et $\ \widehat{KIJ}$ par leur valeur, on obtient :
$\begin{array}{rcl}\widehat{JKI}&=&180^{\circ}-(\widehat{IJK}+\widehat{KIJ})\\\\&=&180^{\circ}-(31.25^{\circ}+37.5^{\circ})\\\\&=&180^{\circ}-68.75^{\circ}\\\\&=&111.25^{\circ}\end{array}$
D'où, $\boxed{\widehat{JKI}=111.25^{\circ}}$
$-\ $ Calcul de $\widehat{AKJ}$
On a : $\widehat{AKJ}\ $ et $\ \widehat{JKI}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{AKJ}+\widehat{JKI}=180^{\circ}$
Ce qui entraine alors : $\widehat{AKJ}=180^{\circ}-\widehat{JKI}$
En remplaçant $\widehat{JKI}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{AKJ}&=&180^{\circ}-\widehat{JKI}\\\\&=&180^{\circ}-111.25^{\circ}\\\\&=&68.75^{\circ}\end{array}$
D'où, $\boxed{\widehat{AKJ}=68.75^{\circ}}$
4) Les droites $(JK)\ $ et $\ (BI)$ ne sont pas parallèles.
Justifions notre réponse.
En effet, les droites $(JK)\ $ et $\ (BI)$ coupées par la droite sécante $(IJ)$, déterminent deux angles alternes-internes $\widehat{BIJ}\ $ et $\ \widehat{IJK}.$
Or, on a : $\widehat{BIJ}=37.5^{\circ}\ $ et $\ \widehat{IJK}=31.25^{\circ}.$
On constate alors que ces deux angles n'ont pas la même mesure.
Par conséquent, les droites $(JK)\ $ et $\ (BI)$ ne sont pas parallèles.

Exercice 13
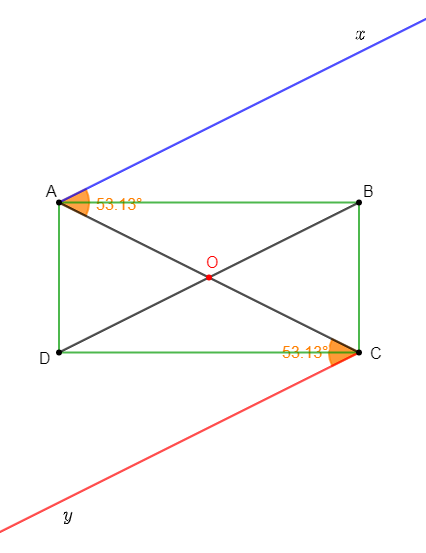
1) Traçons un rectangle $ABCD$ de centre $O$ et construisons :
$[Ax)$ symétrique de $(AC)$ par rapport à $(AB)$
$[Cy)$ symétrique de $(AC)$ par rapport à $(CD).$
2) Les demi-droites $[Ax)\ $ et $\ [Cy)$ sont parallèles
Justifions notre réponse.
En effet, les demi-droites $[Ax)\ $ et $\ [Cy)$ coupées par la droite sécante $(AC)$, déterminent deux angles alternes-internes $\widehat{xAO}\ $ et $\ \widehat{OCy}.$
En mesurant, on constate que ces deux angles alternes-internes ont la même mesure de $53.13^{\circ}.$
Par conséquent, $[Ax)\ $ et $\ [Cy)$ sont parallèles.

Exercice 14
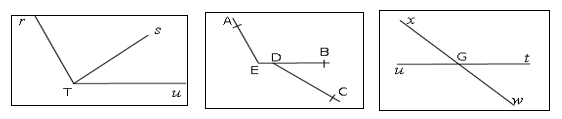
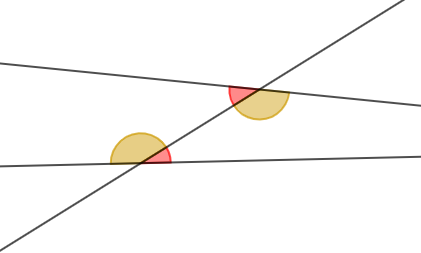
Considérons les figures ci-dessous :

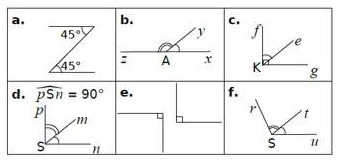
a) Les angles $\widehat{rTs}\ $ et $\ \widehat{sTu}$ sont adjacents.
Ces deux angles ont un sommet commun $T$, un côté commun $[TS)$ et sont situés de part et d'autre de ce côté commun.
Par conséquent, ils sont adjacents
b) Les angles $\widehat{AEB}\ $ et $\ \widehat{BDC}$ ne sont pas adjacents.
En effet, on constate que ces deux angles n'ont pas de sommet commun.
Par conséquent, ils ne sont pas adjacents.
c) Les angles $\widehat{xGu}\ $ et $\ \widehat{tGx}$ sont adjacents.
$\widehat{xGu}\ $ et $\ \widehat{tGx}$ ont un sommet commun $G$, un côté commun $[Gx)$ et sont situés de part et d'autre de ce côté commun.
Alors, ils sont adjacents.
De plus, ils sont supplémentaires
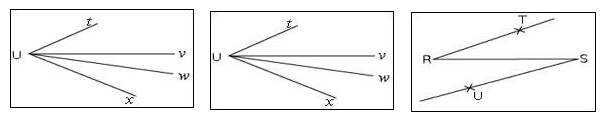
Considérons les figures suivantes :

d) Les angles $\widehat{vUx}\ $ et $\ \widehat{wUv}$ ne sont pas adjacents.
En effet, on remarque que ces deux angles sont situés du même côté du bord commun $[Uv).$
Par conséquent, ils ne sont pas adjacents.
e) Les $\widehat{tUv}\ $ et $\ \widehat{wUx}$ ne sont pas adjacents.
On constate que ces deux angles n'ont pas de côté commun.
Par conséquent, ils ne sont pas adjacents.
f) Les angles $\widehat{TRS}\ $ et $\ \widehat{RSU}$ ne sont pas adjacents.
En effet, on remarque que $\widehat{TRS}\ $ et $\ \widehat{RSU}$ n'ont pas de sommet commun.
Donc, ils ne sont pas adjacents.
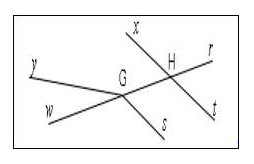
Exercice 15
On donne la figure ci-dessous.

a) $\widehat{yGw}\ $ et $\ \widehat{HGs}$ ne sont pas opposés par le sommet
b) $\widehat{rHx}\ $ et $\ \widehat{tHw}$ sont opposés par le sommet $H$
c) $\widehat{rHt}\ $ et $\ \widehat{xHG}\ $ sont opposés par le sommet $H$
Exercice 16
On donne la figure ci-dessous.

Reproduisons puis complétons le tableau ci-dessous
$$\begin{array}{|c|c|c|c|c|} \hline \text {Angles}&\widehat{xFr}&\widehat{yFt}&\widehat{sFr}&\widehat{sFw}\\\hline\text{Angles opposés par le sommet}&\widehat{wFt}&\widehat{xFs}&\widehat{yFw}&\widehat{yFr}\\\hline\end{array}$$
Exercice 17
On considère les figures $a\;,\ b\;,\ c\;,\ d\;,\ e\;,\ f$ ci-dessous :

Reproduisons et remplissons le tableau ci-dessous en mettant une croix dans la ou les cases qui correspondent à des angles adjacents, complémentaires, supplémentaires.
$$\begin{array}{|l|c|c|c|c|c|c|}\hline\text{Angles}\setminus\text{Figures}&a.&b.&c.&d.&e.&f.\\\hline\text{Angles adjacents}&&\times&\times&\times&&\times\\\hline\text{Angles complémentaires}&\times&&\times&\times&&\\\hline\text{Angles suplémentaires}&&\times&&&\times&\\\hline\end{array}$$
Exercice 18
Reproduisons et remplissons le tableau ci-dessous en mettant une croix dans la case qui convient.
$$\begin{array}{|c|c|c|c|c|}\hline\widehat{a}&\widehat{b}&\text{Complémentaires}&\text{Suplémentaires}&\text{ni l'un, ni l'autre}\\\hline 35^{\circ}&55^{\circ}&\times&&\\\hline 115&65^{\circ}&&\times&\\\hline 47^{\circ}&134^{\circ}&&&\times\\\hline 22^{\circ}&67^{\circ}&&&\times\\\hline 30^{\circ}&150^{\circ}&&\times&\\\hline\end{array}$$
Exercice 19
1) Soient $\widehat{a}\ $ et $\ \widehat{b}$ deux angles complémentaires.
Calculons la mesure de l'angle $\widehat{b}$ dans chacun des cas suivants :
$$\widehat{a}=57^{\circ}\;;\ \widehat{a}=24^{\circ}\;;\ \widehat{a}=2\widehat{b}$$
Comme $\widehat{a}\ $ et $\ \widehat{b}$ deux angles complémentaires alors, cela signifie :
$$\widehat{a}+\widehat{b}=90^{\circ}$$
Ce qui entraine :
$$\widehat{b}=90^{\circ}-\widehat{a}$$
Donc, dans chaque cas, on remplace $\widehat{a}$ par sa valeur pour obtenir la mesure de $\widehat{b}.$
$-\ $ pour $\widehat{a}=57^{\circ}$, on a :
$\begin{array}{rcl}\widehat{b}&=&90^{\circ}-\widehat{a}\\\\&=&90^{\circ}-57^{\circ}\\\\&=&33^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{b}=33^{\circ}}$
$-\ $ pour $\widehat{a}=24^{\circ}$, on a :
$\begin{array}{rcl}\widehat{b}&=&90^{\circ}-\widehat{a}\\\\&=&90^{\circ}-24^{\circ}\\\\&=&66^{\circ}\end{array}$
Donc, $\boxed{\widehat{b}=66^{\circ}}$
$-\ $ pour $\widehat{a}=2\widehat{b}$, on a :
$\widehat{a}+\widehat{b}=90^{\circ}$ si, et seulement si, $2\widehat{b}+\widehat{b}=90^{\circ}$
Ainsi, $3\widehat{b}=90^{\circ}$
Ce qui donne alors : $\widehat{b}=\dfrac{90^{\circ}}{3}=30^{\circ}$
D'où, $\boxed{\widehat{b}=30^{\circ}}$
2) Soient $\widehat{a}\ $ et $\ \widehat{b}$ deux angles supplémentaires.
Calculons la mesure de l'angle $\widehat{b}$ dans chacun des cas suivants :
$$\widehat{a}=127^{\circ}\;;\ \widehat{a}=86^{\circ}\;;\ \widehat{a}=3\widehat{b}$$
Comme $\widehat{a}\ $ et $\ \widehat{b}$ deux angles complémentaires alors, on a :
$$\widehat{a}+\widehat{b}=180^{\circ}$$
Ce qui entraine :
$$\widehat{b}=180^{\circ}-\widehat{a}$$
Donc, dans chaque cas, on remplace $\widehat{a}$ par sa valeur pour obtenir la mesure de $\widehat{b}.$
$-\ $ pour $\widehat{a}=127^{\circ}$, on a :
$\begin{array}{rcl}\widehat{b}&=&180^{\circ}-\widehat{a}\\\\&=&180^{\circ}-127^{\circ}\\\\&=&53^{\circ}\end{array}$
Donc, $\boxed{\widehat{b}=53^{\circ}}$
$-\ $ pour $\widehat{a}=86^{\circ}$, on a :
$\begin{array}{rcl}\widehat{b}&=&180^{\circ}-\widehat{a}\\\\&=&180^{\circ}-86^{\circ}\\\\&=&94^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{b}=66^{\circ}}$
$-\ $ pour $\widehat{a}=3\widehat{b}$, on a :
$\widehat{a}+\widehat{b}=180^{\circ}$ si, et seulement si, $3\widehat{b}+\widehat{b}=180^{\circ}$
Ce qui signifie que : $4\widehat{b}=180^{\circ}$
Ce qui donne alors : $\widehat{b}=\dfrac{180^{\circ}}{4}=45^{\circ}$
D'où, $\boxed{\widehat{b}=45^{\circ}}$
Exercice 20
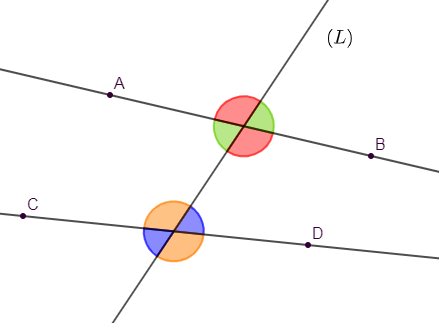
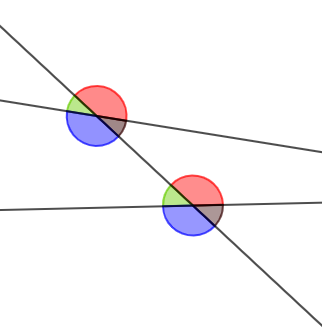
Reproduisons la figure ci-dessous puis colorions différemment les paires d'angles correspondants.

Exercice 21
Reproduisons la figure ci-dessous puis colorions différemment les paires d'angles alternes-internes.

Exercice 22
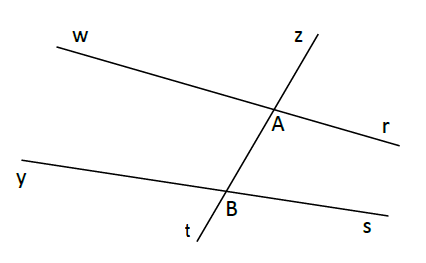
Recopions puis complétons les phrases ci-dessous en nous aidant de la figure ci-dessous :
a) $\widehat{zAr}\ $ et $\ \widehat{zBs}$ sont correspondants
b) $\widehat{rAt}\ $ et $\ \widehat{yBz}$ sont alternes-internes
c) $\widehat{zAr}\ $ et $\ \widehat{zBs}$ sont correspondants
d) $\widehat{zBs}\ $ et $\ \widehat{yBt}$ sont opposés par le sommet.
e) $\widehat{rAt}\ $ et $\ \widehat{sBt}$ sont correspondants.
f) $\widehat{ABs}\ $ et $\ \widehat{wAB}$ sont alternes-internes.

Exercice 23
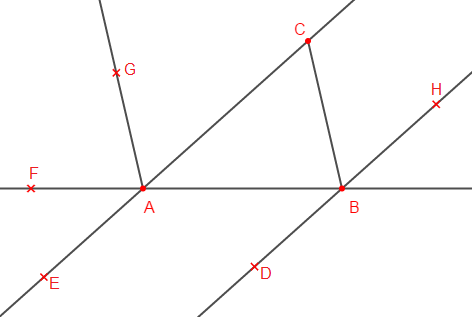
Reproduisons la figure en plaçant les points $D\;,\ E\;,\ F\;,\ G\ $ et $\ H$ sachant que :
$\centerdot\ \ $ les angles $\widehat{BAC}\ $ et $\ \widehat{ABD}$ sont alternes-internes;
$\centerdot\ \ $ les angles $\widehat{CAB}\ $ et $\ \widehat{BAE}$ sont supplémentaires;
$\centerdot\ \ $ les angles $\widehat{CAB}\ $ et $\ \widehat{EAF}$ sont des angles opposés par le sommet;
$\centerdot\ \ $ les angles $\widehat{ABC}\ $ et $\ \widehat{FAG}$ sont correspondants;
$\centerdot\ \ $ les angles $\widehat{ACB}\ $ et $\ \widehat{CBH}$ sont alternes-internes.

Exercice 24
On considère la figure ci-dessous.

1) Citons deux paires d'angles correspondants déterminés par les droites $(EG)\;,\ (AD)$ et la sécante $(KC)$
$$\widehat{CDJ}\ \text{ et }\ \widehat{KFI}\;;\quad\widehat{EFC}\ \text{ et }\ \widehat{BDH}$$
2) Citons deux paires d'angles alternes-internes déterminés par les droites $(EG)\;,\ (AD)$ et la sécante $(BR)$
$$\widehat{ABC}\ \text{ et }\ \widehat{CIG}\;;\quad\widehat{CBD}\ \text{ et }\ \widehat{CIF}$$
3) Citons deux paires d'angles alternes-externes déterminés par les droites $(EG)\;,\ (AD)$ et la sécante $(BR)$
$$\widehat{ABR}\ \text{ et }\ \widehat{GIL}\;;\quad\widehat{DBR}\ \text{ et }\ \widehat{FIL}$$
4) Citons deux paires d'angles opposés par le sommet
$$\widehat{EFK}\ \text{ et }\ \widehat{CFI}\;;\quad\widehat{BCF}\ \text{ et }\ \widehat{DCI}$$
Exercice 25
1) Reproduisons la figure ci-dessous puis colorions avec la même couleur les angles de même mesure sachant que les droites $(AB)\ $ et $\ (CD)$ ne sont pas parallèles.

2) Reproduisons la figure ci-dessous puis colorions avec la même couleur les angles de même mesure sachant que les droites $(AB)\ $ et $\ (CD)$ sont parallèles.

Exercice 26
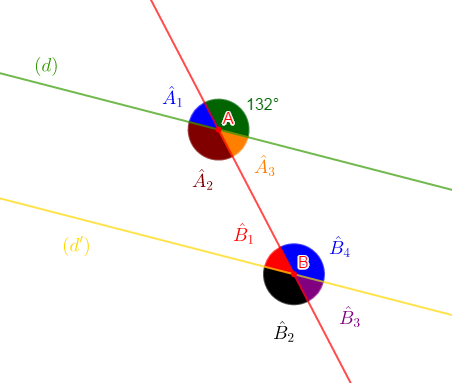
Dans la figure ci-dessous, les droites $(d)\ $ et $\ (d')$ sont parallèles.
Donnons la mesure de chacun des angles
$$\widehat{A}_{1}\;;\ \widehat{A}_{2}\;;\ \widehat{A}_{3}\;;\ \widehat{B}_{1}\;;\ \widehat{B}_{2}\;;\ \widehat{B}_{3}\ \text{ et }\ \widehat{B}_{4}$$
On a :
$\widehat{A}_{2}$ et l'angle de $132^{\circ}$ sont opposés par le sommet $A$ donc, ils ont la même mesure.
Ainsi, $\boxed{\widehat{A}_{2}=132^{\circ}}$
$\widehat{A}_{1}$ et l'angle de $132^{\circ}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{A}_{1}+132^{\circ}=180^{\circ}$
Ce qui entraine alors : $\widehat{A}_{1}=180^{\circ}-132^{\circ}=48^{\circ}$
D'où, $\boxed{\widehat{A}_{1}=48^{\circ}}$
$\widehat{A}_{1}\ $ et $\ \widehat{A}_{3}$ sont opposés par le sommet $A$ donc, ils sont de même mesure.
Par conséquent, $\boxed{\widehat{A}_{3}=48^{\circ}}$
Comme les droites $(d)\ $ et $\ (d')$ sont parallèles alors, $\widehat{A}_{1}\ $ et $\ \widehat{B}_{3}$ sont deux angles alternes-externes de même mesure.
D'où, $\boxed{\widehat{B}_{3}=48^{\circ}}$
$\widehat{B}_{1}\ $ et $\ \widehat{B}_{3}$ sont opposés par le sommet $B$ donc, ils sont de même mesure.
Par conséquent, $\boxed{\widehat{B}_{1}=48^{\circ}}$
$\widehat{B}_{4}\ $ et l'angle de $132^{\circ}$ sont deux angles correspondants de même mesure.
Donc, $\boxed{\widehat{B}_{4}=132^{\circ}}$
$\widehat{B}_{2}\ $ et $\ \widehat{B}_{4}$ sont opposés par le sommet $B$ donc, ils ont la même mesure.
D'où, $\boxed{\widehat{B}_{2}=132^{\circ}}$

Exercice 27
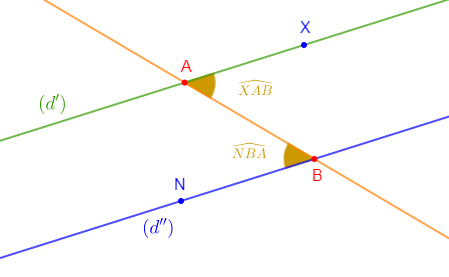
Dans la figure ci-dessous, les droites $(d')\ $ et $\ (d'')$ sont parallèles.
Démontrons que les angles $\widehat{XAB}\ $ et $\ \widehat{NBA}$ ont la même mesure.
En effet, les angles $\widehat{XAB}\ $ et $\ \widehat{NBA}$ sont alternes-internes.
Or, on sait que : deux droites parallèles coupées par une sécante, déterminent deux angles alternes-internes de même mesure.
Comme les droites $(d')\ $ et $\ (d'')$ sont parallèles alors, les les angles $\widehat{XAB}\ $ et $\ \widehat{NBA}$ ont la même mesure.
D'où, les angles $\boxed{mes\;\widehat{XAB}=mes\;\widehat{NBA}}$

Exercice 28
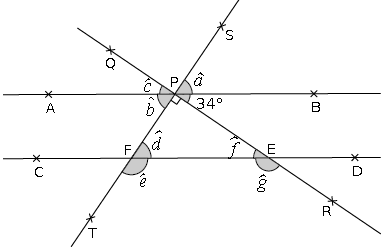
Sachant que dans cette figure les droites $(AB)\ $ et $\ (CD)$ sont parallèles, donnons la mesure de chacun des angles ci-dessous sans mesurer :
$$\widehat{a}\;;\ \widehat{b}\;;\ \widehat{c}\;;\ \widehat{d}\;;\ \widehat{e}\;;\ \widehat{f}\ \text{ et }\ \widehat{g}$$
En effet, comme les droites $(AB)\ $ et $\ (CD)$ sont parallèles alors, les angles alternes-internes ou alternes-externes ou encore correspondants ont la même mesure.
On a : $\widehat{f}$ et l'angle de $34^{\circ}$ sont alternes-internes.
Donc, ils ont la même mesure.
D'où, $\boxed{\widehat{f}=34^{\circ}}$
On a : $\widehat{c}\ $ et l'angle de $34^{\circ}$ sont opposés par le sommet $P$ donc, ils sont de même mesure.
Par conséquent, $\boxed{\widehat{c}=34^{\circ}}$
On a : $\widehat{a}$ et l'angle de $34^{\circ}$ sont adjacents complémentaires.
Ce qui signifie que : $\widehat{a}+34^{\circ}=90^{\circ}$
Ce qui entraine alors : $\widehat{a}=90^{\circ}-34^{\circ}=56^{\circ}$
D'où, $\boxed{\widehat{a}=56^{\circ}}$
On a : $\widehat{b}\ $ et $\ \widehat{a}$ sont opposés par le sommet $P$ donc, ils ont la même mesure.
Par conséquent, $\boxed{\widehat{b}=56^{\circ}}$
On a : $\widehat{d}\ $ et $\ \widehat{b}$ sont alternes-internes donc, ils ont la même mesure.
Ainsi, $\boxed{\widehat{d}=56^{\circ}}$
On a : $\widehat{e}\ $ et $\ \widehat{d}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{e}+\widehat{d}=180^{\circ}$
Ce qui entraine alors : $\widehat{e}=180^{\circ}-\widehat{d}$
En remplaçant $\widehat{d}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{e}&=&180^{\circ}-\widehat{d}\\\\&=&180^{\circ}-56^{\circ}\\\\&=&124^{\circ}\end{array}$
D'où, $\boxed{\widehat{e}=124^{\circ}}$
On a : $\widehat{g}\ $ et $\ \widehat{f}$ sont adjacents supplémentaires.
Ce qui signifie que : $\widehat{g}+\widehat{f}=180^{\circ}$
Ce qui entraine alors : $\widehat{g}=180^{\circ}-\widehat{f}$
En remplaçant $\widehat{f}$ par sa valeur, on obtient :
$\begin{array}{rcl}\widehat{g}&=&180^{\circ}-\widehat{f}\\\\&=&180^{\circ}-34^{\circ}\\\\&=&146^{\circ}\end{array}$
Ainsi, $\boxed{\widehat{g}=146^{\circ}}$

Exercice 29
Dans la figure ci-dessous, les droites $(d')\ $ et $\ (d'')$ sont bien parallèles.
Justifions notre réponse.
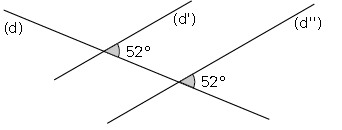
En effet, les droites $(d')\ $ et $\ (d'')$ coupées par la droite sécante $(d)$, déterminent deux angles correspondants de même mesure de $52^{\circ}.$
Par conséquent, les droites $(d')\ $ et $\ (d'')$ sont parallèles.

Exercice 30
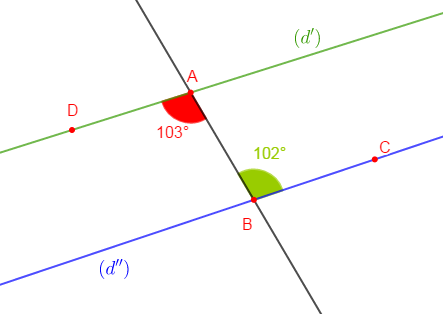
Dans la figure ci-dessous, $\widehat{DAB}=103^{\circ}\ $ et $\ \widehat{CBA}=102^{\circ}.$
Les droites $(d')\ $ et $\ (d'')$ ne sont pas parallèles.
Justifions notre réponse.
En effet, les droites $(d')\ $ et $\ (d'')$ coupées par la droite sécante $(AB)$, déterminent deux angles alternes-internes $\widehat{DAB}\ $ et $\ \widehat{CBA}.$
Or, on constate que ces deux angles alternes-internes n'ont pas la même mesure.
Par conséquent, les droites $(d')\ $ et $\ (d'')$ ne sont pas parallèles.

Auteur:
Diny Faye

Commentaires
ordinateur fort (non vérifié)
lun, 03/15/2021 - 20:20
Permalien
merci
Gueye (non vérifié)
dim, 05/09/2021 - 15:23
Permalien
Correction exercice 3
Gueye (non vérifié)
dim, 05/09/2021 - 15:24
Permalien
Correction exercice 3
ordinateur fort (non vérifié)
lun, 03/15/2021 - 20:21
Permalien
merci
Gueye (non vérifié)
dim, 05/09/2021 - 15:12
Permalien
Bien
Anonyme (non vérifié)
dim, 03/13/2022 - 20:56
Permalien
Les angles orthocentre
Anonyme (non vérifié)
lun, 03/14/2022 - 07:30
Permalien
Je veux la correction de l
Elhadji (non vérifié)
dim, 04/10/2022 - 13:54
Permalien
Auc
Anonyme (non vérifié)
lun, 03/14/2022 - 07:30
Permalien
Je veux la correction de l
Ly (non vérifié)
mer, 04/13/2022 - 00:21
Permalien
Pourquoi y'a des exercices
Anonyme (non vérifié)
mar, 01/17/2023 - 19:54
Permalien
Je me débrouille bien avec
Anonyme (non vérifié)
lun, 12/11/2023 - 17:06
Permalien
Je veux exercices 1vrai ou
Ajouter un commentaire