Exercices : Les parallélogrammes 5e
Classe:
Cinquième
Exercice 1
1) Construire un triangle $ABC$ tel que : $AB=3\;cm\;;\ AC=4\;cm$ et $BC=5.5\;cm.$
2) a) Construire le point $D$ pour que le quadrilatère $ABCD$ soit un parallélogramme.
b) Construire le point $E$ pour que le quadrilatère $ABEC$ soit un parallélogramme.
c) Construire le point $F$ pour que le quadrilatère $AFBC$ soit un parallélogramme.
Consigne : Pour la construction des points $D\;,\ E$ et $F$ ; utiliser trois méthodes différentes.
Exercice 2
1) Construire un triangle $ABC$ tel que : $AB=5\;cm\;;\ mes\;\widehat{A}=30^{\circ}$ et $mes\;\widehat{B}=50^{\circ}.$
2) a) Placer le point $I$ milieu du segment $[BC].$
b) Placer le point $K$ symétrique de $A$ par rapport au point $I.$
3) Quelle est la nature du quadrilatère $ABKC$ ? Justifier la réponse.
4) Calculer : $mes\;\widehat{BKC}\;;\ mes\;\widehat{ABK}$ et $mes\;\widehat{CBK}.$
Exercice 3
1) Soit $MNP$ un triangle tel que : $MN=4\;cm\;;\ NP=6\;cm$ et $MP=5\;cm.$
2) Tracer la droite $(d)$ passant par $P$ et parallèle à $(MN).$
3) Tracer la droite $(d')$ passant par $M$ et parallèle à $(PN).$
4) a) Soit $E$ le point d'intersection de $(d)$ et $(d').$
b) Quelle est la nature de $MNPE\ ?$ Justifier.
5) Quelle est la longueur des segments $[ME]$ et $[PE]$ ?
Exercice 4
$ABCD$ est un parallélogramme de centre $O.$
1) Comparer les angles de sommet $O.$
2) Comparer les angles de sommets $A$ et $C.$
3) Que peut-on dire les angles de sommets $A$ et $B.$
Exercice 5
1) Soit $ABC$ un triangle tel que : $AB=4\;cm\;;\ AC=5\;cm$ et $BC=5.5\;cm.$
2) Placer les points $I$ et $J$ milieux respectifs des segments $[AB]$ et $[AC].$
3) Construire les points $D$ et $E$ tel que :
Le point $D$ est le symétrique de $B$ par rapport à $J.$
Le point $E$ est le symétrique de $C$ par rapport à $I.$
4) Quelle est la nature des quadrilatères $ABCD$ et $ACBE$ ? Justifier les réponses.
Exercice 6
1) Trace un triangle $ABC.$
2) Trace les hauteurs issues des sommets $B$ et $C$ ; ces hauteurs se coupent au point $I.$
3) Construire la droite perpendiculaire à $(AC)$ passant par $C$ et la droite perpendiculaire à $(AB)$ passant par $B$ ; ces perpendiculaires se coupent au point $O.$
4) Quelle est la nature de $CIBO$ ? Justifier.
Exercice 7
Soit $ABC$ un triangle ; $M$ est le milieu de $[BC].$
1) Construire le point $D$ symétrique de $B$ par rapport au point $A.$
2) Construire le point $N$ symétrique de $M$ par rapport au point $A.$
3) Montrer que le quadrilatère $BMDN$ est un parallélogramme.
4) a) Montrer que : $ND=MC$ puis $(ND)//(MC).$
b) En déduire que le quadrilatère $CDNM$ est un parallélogramme.
Exercice 8
$ABC$ est un triangle ; $I$ et $J$ sont des milieux respectifs des segments $[BC]$ et $[AC].$
1) Construire le point $A'$ symétrique de $A$ par rapport au point $I.$
2) Construire le point $B'$ symétrique de $B$ par rapport au point $J.$
3) Montrer que les quadrilatères $ABA'C$ et $ABCB'$ sont des parallélogrammes.
4) En déduire que $C$ est le milieu du segment $[A'B'].$
Exercice 9
1) Construis le parallélogramme $ABCD$ de centre $O.$
2) Construis le point $E$ tel que le quadrilatère $ABEC$ soit un parallélogramme.
3) Construis le point $F$ tel que le quadrilatère $ABDF$ soit un parallélogramme.
Exercice 10
1) Place trois points $E\;,\ F\ $ et $\ G$ distincts et non alignés.
2) Construis le point $H$ tel que le quadrilatère $EFGH$ soit un parallélogramme.
3) Construis le point $I$ tel que le quadrilatère $EFIG$ soit un parallélogramme.
4) Construis le point $J$ tel que le quadrilatère $EGFJ$ soit un parallélogramme.
Exercice 11
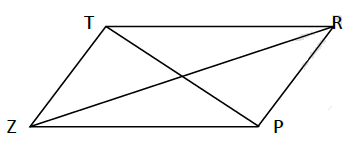
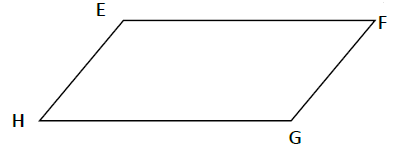
Les parallélogrammes ci-dessous ne sont pas en vraie grandeur.
Représente-les en vraie grandeur.

$TP=4\;cm\;;\ ZT=6\;cm\;;\ ZP=4.5\;cm$

$EF=6.5\;cm\;;\ FG=3.5\;cm\;;\ \widehat{EFG}=55^{\circ}$
Exercice 12
Dans chacun des cas ci-dessous, construis le parallélogramme $ABCD$ tel que :
1) $AB=4\;cm\;;\ \widehat{BAC}=48^{\circ}\ $ et $\ \widehat{ADC}=102^{\circ}.$
2) $AC=5\;cm\;;\ CD=8\;cm\ $ et $\ BC=7.5\;cm$
3) $AB=6.5\;cm\;;\ BC=7.5\;cm\ $ et $\ \widehat{ADC}=122^{\circ}.$
Exercice 13
$RSUT$ est un parallélogramme.
Justifie que :
1) $TU=RS$,
2) $2\times RI=RU$ où $I$ est le point d'intersection de $[RU]\ $ et $\ [ST].$
3) $\widehat{TUS}=\widehat{TRS}.$
Exercice 14
En utilisant la règle et le compas, construis :
1) un parallélogramme $ABCD$, tel que $DA=3\;cm\;,\ BA=5\;cm.$
2) un parallélogramme $EFGH$ tel que $HE=35\;mm\ $ et $\ \widehat{GHE}=50^{\circ}.$
Exercice 15
Construis un losange $MATH$ tel que $MA=5\;cm\ $ et $\ \widehat{ATH}=54^{\circ}.$
Exercice 16
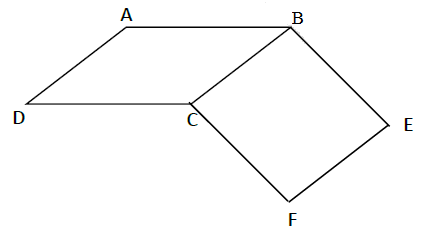
On considère la figure ci-dessous où $ABCD\ $ et $\ BEFC$ sont des parallélogrammes.
1) Donne, en justifiant, deux droites parallèles à la droite $(BC).$
2) Démontre que $AEFD$ est un parallélogramme.
3) Démontre que les segments $[AF]\ $ et $\ [ED]$ se coupent en leur milieu.

Exercice 17
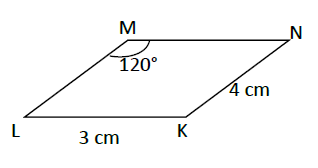
Dans la figure ci-dessous, le quadrilatère dessiné est un parallélogramme.
Donne les longueurs ou les angles demandés. Justifie en citant les propriétés utilisées.
$$LM\;;\ MN\;;\ \widehat{LKN}\;;\ \widehat{KLM}\;;\ \widehat{KNM}$$

Exercice 18
1) Construis le parallélogramme $EFGH$ de centre $I$ tel que :
$$\widehat{EIF}=35^{\circ}\;;\ EG=4\;cm\ \text{ et }\ FH=6\;cm$$
en donnant un programme de construction.
2) Construis le parallélogramme ROSE tel que :
$OR=5\;cm\;;\ RE=4\;cm\ $ et $\ \widehat{OER}=30^{\circ}.$
3) Construis le parallélogramme $PAUL$ tel que :
$PU=8\;cm\;;\ LA=5\;cm\ $ et $\ LU=3\;cm.$
Exercice 19
1) Trace le triangle $EFG$ tel que :
$$EF=5\;cm\;;\ \widehat{GEF}=70^{\circ}\ \text{ et }\ \widehat{EFG}=50^{\circ}$$
Quelle est la mesure de l'angle $\widehat{EGF}\ ?$
2) Construis le point H tel que $EHGF$ soit un parallélogramme.
Quelle est la mesure de $\widehat{GEH}\ ?$ Justifie.
Exercice 20
1) Construis le parallélogramme $ABCD$ de centre $O$ tel que :
$$AB=8\;cm\;,\ \widehat{BAC}=40^{\circ}\ \text{ et }\ \widehat{ABD}=30^{\circ}$$
2) Place le point $I$ milieu de $[AB]$ et le point $J$ milieu de $[BC].$
3) Construis $E$ symétrique de $D$ par rapport à $I$ et le point $F$ symétrique de $D$ par rapport à $J.$
4) Quelle est la nature des quadrilatères $AEBD\ $ et $\ DBFC\ ?$ Justifie ta réponse.
5) Les points $A\;,\ B\ $ et $\ F$ sont-ils alignés ? Justifie ta réponse.
Exercice 21
$ABCD$ est un parallélogramme de centre $O.$
1) Compare les mesures des angles $\widehat{AOB}\ $ et $\ \widehat{DOC}.$ Justifie.
2) Compare les mesures des angles $\widehat{BAD}\ $ et $\ \widehat{DCB}.$ Justifie.
Exercice 22
Soit $ABCD$ un quadrilatère tel que :
$AD=2\;cm\;,\ AB=5.2\;cm\;,\ DB=4.8\;cm\;,\ BC=1.4\;cm\ $ et $\ DC=5\;cm.$
$ABCD$ est-il un parallélogramme ? Justifie ta réponse.
Exercice 23
1) Soit $ABDC$ un parallélogramme tel que $AB=6\;cm\;,\ BD=8\;cm\ $ et $\ (AB)$ perpendiculaire à $(BD).$ Le cercle circonscrit au triangle $ABD$ a pour rayon $5\;cm.$
Calcule $BC.$
2) Calcule le périmètre et l'aire de $ABDC.$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Anonyme (non vérifié)
dim, 12/27/2020 - 19:07
Permalien
J'aime
Anonyme (non vérifié)
dim, 01/17/2021 - 20:50
Permalien
Comment on fait ses exercices
Bassirou gueye (non vérifié)
ven, 07/02/2021 - 12:35
Permalien
C'est très intéressant
Bathie fall (non vérifié)
lun, 03/28/2022 - 00:24
Permalien
exercice 9et10
Ajouter un commentaire