Exercices : Symétrie centrale 5e
Classe:
Cinquième
Exercice 1
1) Tracer un segment $[AB]$ tel que $AB=5\;cm.$ Construire son milieu $I.$ Que peut-on dire des points $A$ et $B$ par rapport à $I\ ?$ Justifier la réponse.
2) Tracer un segment $[EF]$ dont $I$ est le milieu. Quel est le symétrique de $E$ par rapport à $I\ ?$ Justifier la réponse.
3) Marque un point $M$, construire son symétrique par rapport à $I.$
Exercice 2
1) Trace un triangle équilatéral $ABC$ tel que $AB=5\;cm.$
2) Construire un point $O$ extérieur du triangle de $ABC.$
3) Construire les points $A'\;,\ B'\ $ et $\ C'$ symétriques de $ABC$ par rapport à $O.$
4) Quelle est la nature du triangle $A'B'C'\ ?$ Justifier la réponse par une propriété du cours.
Exercice 3
Soit $ABCD$ un carré de côté $4\;cm.$
1) Construire le point $O$ centre de symétrique de $ABCD.$
2) Construire les points $E\;;\ F$ et $G$ symétriques respectifs des points $B\;;\ C\ $ et $\ D$ par rapport à $A.$
3) a) Quelle est le symétrique de $ABCD$ par rapport à $A.$
b) En utilisant la figure compléter :
$S_{A}(A)=\ldots\;;\ S_{A}(CD)=\ldots\;;\ S_{A}([AD))=\ldots$
4) Quelle est la nature de $AEFG$ puis calculer son aire.
Exercice 4
On considère le parallélogramme $ABPQ$ de centre $O.$
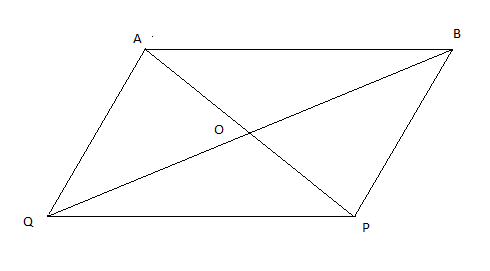
Compléter les pointillés par le point, le segment, la droite ou la demi-droite qui convient.
$S_{O}(A)=\ldots\;;\quad S\ldots(B)=Q$
$S_{O}([AQ])=\ldots\;;\quad S_{O}\ldots=[AB]$
$S_{O}(AQP)=\ldots\;;\quad S_{O}\ldots=(BP)$
$S_{O}([AQ))=\ldots\;;\quad S_{O}\ldots=[PB)$
Exercice 5
1) Construire un triangle $ABC$ tel que :
$$AB=4\;cm\;;\ BC=3\;cm\ \text{ et }\ AC=2\;cm$$
$$AB=4\;cm\;;\ BC=3\;cm\ \text{ et }\ AC=2\;cm$$
2) Construire le triangle $AEF$ symétrique du triangle $ABC$ par rapport à au point $A.$
3) a) Quel est le segment qui a la même longueur que $[EF]\ ?$
b) Nommer les antres segments superposables.
4) a) Quel est l'angle de la figure qui a la même mesure que l'angle $\widehat{E}\ ?$
b) Nommer les antres angles superposables.
Exercice 6
1) Citez cinq lettres alphabet français admettant un centre de symétrique.
2) Citez trois figures géométriques admettant un centre de symétrique.
3) Citez deux figures géométriques qui sont globalement invariant par la symétrie centrale.
Exercice 7
On donne trois points non alignés $M\;;\ O\ $ et $\ D.$
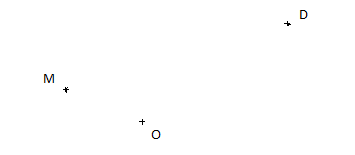
$-\ \ M$ est le milieu d'un segment $[AB].$
$-\ $ Le point $D$ est une extrémité d'un segment $[CD].$
$-\ $ Les segments $[AB]$ et $[CD]$ sont symétriques par rapport à $O.$
Construire les points $A\;,\ B\ $ et $\ C$ en donnant un programme de construction.
(Faire d'abord la figure à main levée).
Exercice 8
Recopie et complète convenablement les phrases suivantes :
1) Si $A\ $ et $\ B$ sont deux points $\ldots\ldots\ldots$ par rapport à un point $O$, alors $O$ est le milieu de $\ldots\ldots\ldots$
2) Si $K$ est le milieu de $[RS]$ alors les points $\ldots\ldots\ldots$ sont $\ldots\ldots\ldots$ par rapport à $\ldots\ldots\ldots$
3) Si $E$ est symétrique de $F$ par rapport à $M$ alors $\ldots\ldots\ldots$ est le milieu de $\ldots\ldots\ldots$
4) Le symétrique d'un segment par rapport à un point est un $\ldots\ldots\ldots$ de même $\ldots\ldots\ldots$
5) La symétrie centrale $\ldots\ldots\ldots$ l'alignement
Exercice 9
Recopie les affirmations qui sont vraies.
1) La symétrie centrale ne conserve pas les longueurs.
2) La symétrie centrale conserve le parallélisme.
3) La symétrie centrale conserve les aires.
4) La symétrie centrale ne conserve pas la perpendicularité.
5) La symétrie centrale conserve la mesure des angles.
6) Le symétrique d'un angle par rapport à un point est un angle de même mesure.
7) Deux angles opposés par le sommet sont symétriques par rapport à ce sommet.
Exercice 10
On considère la droite graduée ci-dessous (unité $1$ centimètre) :
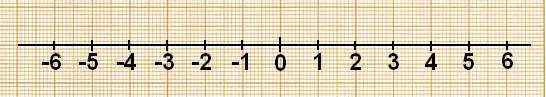
1) Reproduis la droite puis place les points $A\;,\ B\;,\ C\;,\ D\;,\ E\;,\ F\;,\ G\ $ et $\ O$ d'abscisses respectives $$\dfrac{-5}{2}\;;\ -3.5\;;\ -0.5\;;\ \dfrac{1}{2}\;;\ \dfrac{3}{2}\;;\ \dfrac{7}{2}\;;\ 2.5\ \text{ et }\ 0$$
2) Cite les points deux à deux symétriques par rapport au point $O.$
3) Complète la phrase suivante : $[AC]$ est le symétrique de $\ldots\ldots\ldots$ par rapport au point $O.$
Exercice 11
1) Trace un triangle $ABC.$ Marque un point $I$ à l'extérieur du triangle.
2) Place :
$-\ $ le point $E$ symétrique de $A$ par rapport à $I$,
$-\ $ le point $F$ symétrique de $B$ par rapport à $I$,
$-\ $ le point $G$ symétrique de $C$ par rapport à $I.$
Exercice 12
1) Trace un rectangle $EFGH$, puis place un point $O$ à l'intérieur du rectangle.
2) Place :
$-\ $ le symétrique $R$ de $E$ par rapport à $O$,
$-\ $ le symétrique $S$ de $F$ par rapport à $O$,
$-\ $ le symétrique $T$ de $G$ par rapport à $O$,
$- $ le symétrique $U$ de $H$ par rapport à $O.$
3) Quelle est la nature du quadrilatère $RSTU ?$
Exercice 13
Recopie puis complète les phrases ci-dessous :
1) Le symétrique d'un point $M$ par rapport à un point $O$ est le point $M'$ tel que $\ldots\ldots\ldots$
2) Le symétrique d'une droite par rapport à un point $O$ est une droite $\ldots\ldots\ldots$
3) Le symétrique d'un segment par rapport à un point $O$ est un segment $\ldots\ldots\ldots$
4) Le symétrique d'un angle par rapport à un point $O$ est un angle $\ldots\ldots\ldots$
5) Le symétrique d'un cercle par rapport à un point $O$ est un $\ldots\ldots\ldots$
Exercice 14
1) Trace un triangle $ABC.$
2) a) Construis le segment $[A'B']$ symétrique du segment $[AB]$ par rapport au point $C.$
b) Justifie que les segments $[AB]$ et $[A'B']$ ont même longueur.
3) a) Quel est le symétrique du triangle $ABC$ par la symétrie centrale de centre $C\ ?$
b) Compare les aires des triangles $ABC\ $ et $\ A'B'C\ ?$ Justifie ta réponse.
Exercice 15
1) Construis le triangle $EFG$ tel que
$$EF=4\;cm\;;\ FG=6\;cm\ \text{ et }\ EG=5\;cm$$
2) a) Place le point $F'$ symétrique du point $F$ par rapport à $E.$
b) Place le point $G'$ symétrique du point $G$ par rapport à $E.$
3) Quelle est la position relative des droites $(FG)\ $ et $\ (F'G')\ ?$ Justifie ta réponse.
4) Donne, sans les mesurer, les longueurs $EF'\;,\ EG'\ $ et $\ F'G'.$ Justifie ta réponse.
5) Prouve que les droites $(F'G)\ $ et $\ (FG')$ sont parallèles.
Exercice 16
On considère le triangle $ABC$ tel que
$$AB=3\;cm\;;\ AC=5\;cm\ \text{et}\ BC=5\;cm$$
Soit $O$ le milieu du segment $[AB].$
1) Construis le triangle $ABC$ en mettant le codage sur les longueurs.
2) a) Quel est le symétrique du point $A$ par rapport au point $O\ ?$
b) Quel est le symétrique du point $B$ par rapport au point $O\ ?$
3) Trace le symétrique du triangle $ABC$ par rapport à $O.$ Complète le codage des longueurs.
Exercice 17
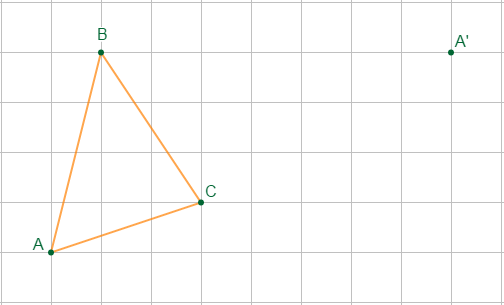
Dans la figure ci-dessous, $A'$ est le symétrique de $A$ par la symétrie de centre $O.$
Le point $O$ n'a pas été placé.
1) Reproduis la figure ci-dessous en t'aidant du quadrillage du cahier
2) Sans utiliser les instruments :
a) retrouve le point $O,$
b) Place $B'\ $ et $\ C'$ symétriques respectifs de $B\ $ et $\ C$ par rapport à $O.$
3) A l'aide de la règle, trace le triangle $A'B'C'.$
Exercice 18
1) Reproduis la figure ci-dessous puis place les points $T\;,\ B\ $ et $\ N$ symétriques respectifs des points $S\;,\ A\ $ et $\ M$ par rapport à $O.$
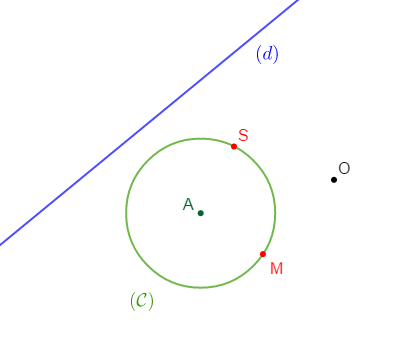
2) Construis le symétrique $C'$ du cercle $C$ par rapport à $O.$
3) Construis le symétrique $(d')$ de la droite $(d)$ par rapport à $O.$
a) Justifie que $AM=BN.$
b) Est-ce qu'on a : $SA=BN\ ?$ Justifie.
c) Quelle est la position relative des droites $(SM)\ $ et $\ (TN)\ ?$ des droites $(d)\ $ et $\ (d')\ ?$ Justifie tes réponses.
Exercice 19
1) Construis le triangle $ABC$ tel que
$$AB=4.5\;cm\;;\ AC=6\;cm\ \text{et}\ BC=4\;cm$$
2) Place les symétriques $A'\ $ et $\ C'$ respectifs de points $A\ $ et $\ C$ par rapport au point $B.$
3) Construis le symétrique du triangle $ABC$ par rapport à $B.$
4) Justifie que les segments $[AC]$ et $[A'C']$ ont même longueur.
5) Quel angle a la même mesure que l'angle $\widehat{BAC}\ ?$ Justifie ta réponse.
Exercice 20
1) Reproduis la figure ci-dessous où les points des triangles $EAC\ $ et $\ NSK$ sont symétriques par rapport à un point $J$ qui a été effacé.
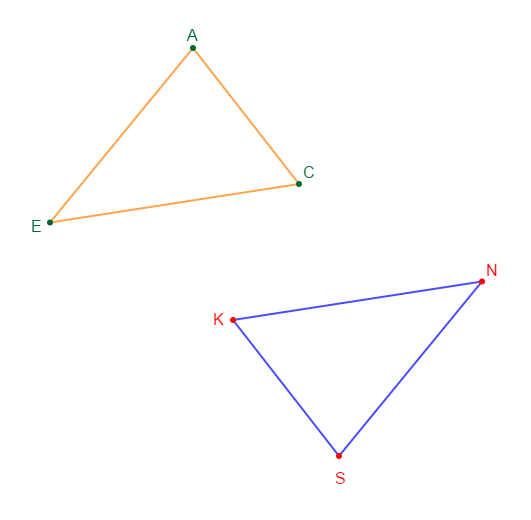
2) Place le point $J.$
3) Les deux triangles ont-ils le même périmètre ? Justifie.
Exercice 21
1) Construis un carré $ABCD$ de coté $4\;cm$ et à l'extérieur de ce carré, construis le triangle $BCI$ rectangle en $C$ tel que $BI=7\;cm.$
2) Complète ta construction de manière à obtenir une figure dont le centre de symétrie est le point $C.$
Exercice 22
1) Construis un triangle $LOP$ rectangle en $O\ $ et $\ LP=6\;cm.$
2) Place le point $M$ symétrique du point $O$ par rapport au point $I$ milieu du segment $[LP].$
3) Construis le point $T$ symétrique du point $M$ par rapport au point $P.$
4) Quelle est la nature des quadrilatères $LOPM\ $ et $\ LOTP\ ?$ Justifie ta réponse.
5) Construis le cercle $(C)$ de centre $I$ et de rayon $IM.$ Calcule le périmètre et l'aire du disque correspondant.
6) Place un point $E$ extérieur au cercle $(C).$ Construis le cercle $(C')$ symétrique de $(C)$ par rapport à $E.$
7) Quelle est la mesure du périmètre du cercle ? Justifie ta réponse.
Exercice 23
1) Construis le triangle $MNP$ tel que
$$MN=7\;cm\;;\ \widehat{MNP}=64^{\circ}\ \text{et}\ NP=10\;cm$$
2) Place le point $A$ sur le segment $[NP]$ tel que $NA=3.5\;cm$
3) On appelle $O$ le milieu du segment $[AM].$ Construis les points $J\ $ et $\ K$ symétriques respectifs des points $N\ $ et $\ P$ par rapport à $O.$
4) Quel est le symétrique du point $A$ par rapport à $O\ ?$ Justifie ta réponse.
5) On veut montrer que les droites $(MN)\ $ et $\ (AJ)$ sont parallèles. Pour cela recopie et complète le texte de démonstration suivant :
Dans la symétrie centrale de centre $O$, $M$ a pour symétrique $\ldots\ldots\ldots$
$N$ a pour symétrique $\ldots\ldots\ldots$
Donc la droite $(MN)$ a pour symétrique $\ldots\ldots\ldots$ et on a $\ldots\ldots\ldots$
6) En utilisant la même démarche montre que les longueurs $JK\ $ et $\ NP$ sont égales.
7) En utilisant la même démarche montre que les angles $\widehat{JPM}\ $ et $\ \widehat{NKA}$ ont même mesure.
8) Montre que les points $K\;,\ M\ $ et $\ J$ sont alignés.
Exercice 24
On donne un segment $[AM].$
1) Construis le triangle $ABC$ tel que $\widehat{ABC}=74^{\circ}\ $ et $\ \widehat{ACB}=58^{\circ}\;,\ B\ $ et $\ C$ distincts de $M.$
2) Place le point $O$ milieu du segment $[AM].$
3) Construis les points $N\ $ et $\ P$ symétriques respectifs des points $B\ $ et $\ C$ par rapport au point $O.$
4) Justifie que $M$ est le symétrique du point $A$ par rapport à $O.$
5) Quelle est la position relative des droites $(AB)\ $ et $\ (NM)\ ?$ Justifie ta réponse.
6) Les points $A\;,\ P\ $ et $\ N$ sont-ils alignés ? Justifie ta réponse.
7) Construis le cercle de diamètre $[AB]$ et appelle $S$ son centre puis construis le symétrique de ce cercle par rapport à $O.$ Quel est son diamètre ?
Exercice 25
Soit $ABC$ un triangle tel que $\widehat{BCA}=30^{\circ}\ $ et $\ (d)$ la hauteur passant par $A$ ; la droite $(d)$ coupe la droite $(BC)$ en $H.$
1) Quelle est la mesure de l'angle $\widehat{HAC}\ ?$
2) Soit les points $D\;,\ E\ $ et $\ F$ symétriques respectifs des points $B\;,\ H\ $ et $\ C$ par rapport au point $A.$
a) Justifie que les points $D\;,\ E\;,\ F$ sont alignés.
b) Quelle est la mesure de l'angle $\widehat{AED}\ ?$ Justifie ta réponse.
c) Construis le cercle circonscrit au triangle $AFD.$
d) Construis le plus simplement possible le cercle circonscrit au triangle $ABC.$
Exercice 26
1) Construis un triangle isocèle $ISO$ en $I$ et place un point $A.$
2) Construis le symétrique $I'S'O'$ du triangle $ISO$ par rapport au point $A.$
3) Le triangle $I'S'O'$ est-il isocèle ? Justifie ta réponse.
4) Construis la hauteur $[Ix)$ du triangle $ISO$ et son symétrique par rapport à $A.$
5) Que représente ce symétrique de $[Ix)$ pour le triangle $I'S'O'\ ?$
Exercice 27
1) Trace le triangle $ABC$ tel que $AC=8\;cm\;;\ \widehat{ABC}=50^{\circ}\ $ et $\ BC=10\;cm$ et place le point $M$ du segment $[BC]$ tel que $CM=3\;cm.\ O$ est le milieu du segment $[AM].$
2) Construis les points $G\ $ et $\ H$ symétriques respectifs des points $B\ $ et $\ C$ par rapport à $O.$
3) Démontre que les longueurs $GH\ $ et $\ BC$ sont égales.
4) Démontre que les droites $(AB)\ $ et $\ (MG)$ sont parallèles.
5) Démontre que les points $A\;,\ G\ $ et $\ H$ sont alignés.
Exercice 28
On considère un quadrilatère $ABCD$ surmonté d'un demi-cercle de diamètre $[AB].$
1) Fais une figure puis construis son symétrique par rapport à B. On appellera $A'\;,\ C'\ $ et $\ D'$ les symétriques respectifs des points $A\;,\ C\ $ et $\ D$ par rapport à $B.$
2) Cite deux segments de même longueur.
3) Démontre que les droites $(AD)\ $ et $\ (A'D')$ sont parallèles.
Exercice 29
La figure $\mathcal{A}_{1}$ ci-dessous représente la lettre $A$ schématisée par trois segments $[MN]\;,\ [NQ]\ $ et $\ [RS].$
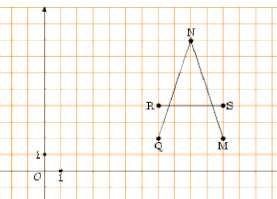
1) Construis la figure $\mathcal{A}_{2}$ symétrique de $\mathcal{A}_{1}$ par rapport à $O.$
2) Construis la figure $\mathcal{A}_{3}$ symétrique de $\mathcal{A}_{1}$ par rapport à l'axe des abscisses.
3) a) Quelles sont les coordonnées des points $M\ $ et $\ N.$
b) Quelles sont les coordonnées des points $M'\ $ et $\ N'$ symétriques respectifs de $M\ $ et $\ N$ par rapport à $O\ ?$
c) Quelles sont les coordonnées des points $M''\ $ et $\ N''$ symétriques respectifs de $M\ $ et $\ N$ par rapport à l'axe des abscisses ?
Exercice 30
1) Reproduis la figure $\mathcal{F}$ ci-dessous.
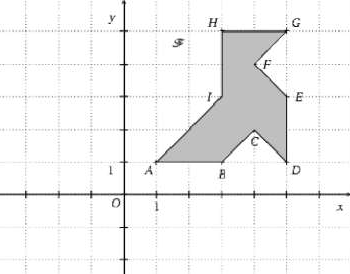
2) Construis et colorie différemment l'image $\mathcal{F}'$ de la figure $\mathcal{F}$ par la symétrie de centre $O.$
3) Recopie et complète le tableau ci-dessous :
$$\begin{array}{|l|c|c|c|c|c|c|}\hline\text{Points}&A&A'&E&E'&G&G'\\\hline\text{Abscisses}&&&&&&\\\hline\text{Ordonnées}&&&&&&\\\hline\end{array}$$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Anonyme (non vérifié)
ven, 11/15/2019 - 21:23
Permalien
Correction
Anonyme (non vérifié)
jeu, 04/30/2020 - 14:06
Permalien
La correction
Mor (non vérifié)
lun, 11/23/2020 - 13:28
Permalien
Merci pour la facilité de
Cheikh Abdoulla... (non vérifié)
dim, 12/20/2020 - 15:21
Permalien
Etude
Amadou ba (non vérifié)
ven, 01/29/2021 - 00:28
Permalien
Apprendre
Cheikh Abdoulla... (non vérifié)
dim, 12/20/2020 - 15:22
Permalien
Travail
Anonyme (non vérifié)
lun, 01/18/2021 - 18:28
Permalien
Ca c'est bon pour les élevées
Anonyme (non vérifié)
lun, 02/15/2021 - 23:04
Permalien
Correction exercice 5 et 7
Anonyme (non vérifié)
jeu, 03/03/2022 - 18:36
Permalien
gg
Anonyme (non vérifié)
lun, 12/12/2022 - 22:05
Permalien
S'il vous plaît arrêté les
MBA bengone jea... (non vérifié)
ven, 04/07/2023 - 19:37
Permalien
Exercice et cours
Anonyme (non vérifié)
ven, 09/01/2023 - 11:12
Permalien
SADA Professeur de
Ajouter un commentaire