Inéquations et système d'inéquations à une inconnue - 4e
Classe:
Quatrième
I. Inéquation
I.1. Définition
On appelle une inéquation à une inconnue toute inégalité dans laquelle se trouve une inconnue.
Exemple
$$\underbrace{2x+3}_{\text{1er membre }}\underbrace{>}_{\text{ l'inégalité }}\underbrace{4}_{\text{ 2nd membre}}$$
Remarque
Dans une inéquation, on peut trouver :
$\begin{array}{lcl}\centerdot\ \text{inégalité stricte :}&>&\text{supérieur strictement}\\&<&\text{inférieur strictement}\\ \\\centerdot\ \text{inégalité large :}&\geq&\text{supérieur ou égal}\\&\leq&\text{inférieur ou égal}\end{array}$
I.2. Résolution de l'inéquation
a) Inéquation du type $ax+b\;\ast\; 0\;,\ a\neq 0\ $ et $\ \ast\in\{>\;,\ <\;,\ \geq\;,\ \leq\}$
Exemple
Résoudre dans $\mathbb{Q}$
1) $2x-16>0$
2) $2x-16<0$
3) $2x-16\geq 0$
4) $2x-16\leq 0$
Solution
1)
$\begin{array}{rcrcl} 2x-16>0&\Leftrightarrow&2x&>&16\\ \\&\Leftrightarrow&x&>&\dfrac{16}{2}\\ \\&\Leftrightarrow&x&>&8\end{array}$

$S=]8\;;\ +\infty[$
La solution est l'ensemble des rationnels $x$ supérieurs strictement à $8.$
2)
$\begin{array}{rcrcl} 2x-16<0&\Leftrightarrow&2x&<&16\\ \\&\Leftrightarrow&x&<&\dfrac{16}{2}\\ \\&\Leftrightarrow&x&<&8\end{array}$

$S=]-\infty\;;\ 8[$
La solution est l'ensemble des rationnels $x$ inférieurs strictement à $8.$
3)
$\begin{array}{rcrcl} 2x-16\geq 0&\Leftrightarrow&2x&\geq&16\\ \\&\Leftrightarrow&x&\geq&\dfrac{16}{2}\\ \\&\Leftrightarrow&x&\geq&8\end{array}$
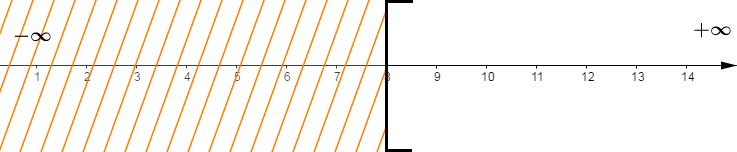
$S=[8\;;\ +\infty[$
La solution est l'ensemble des rationnels $x$ supérieurs ou égaux à $8.$
4)
$\begin{array}{rcrcl} 2x-16\leq 0&\Leftrightarrow&2x&\leq&16\\ \\&\Leftrightarrow&x&\leq&\dfrac{16}{2}\\ \\&\Leftrightarrow&x&\leq&8\end{array}$

$S=]-\infty\;;\ 8]$
La solution est l'ensemble des rationnels $x$ inférieurs ou égaux à $8.$
Remarque
Si $a$ est négatif alors, on résout l'inéquation en changeant le sens de l'inégalité.
Exemple
Résoudre dans $\mathbb{Q}$
1) $-3x\geq 15$
2) $-1>1-4x$
Solution
1)
$\begin{array}{rcrcl} -3x\leq 15&\Leftrightarrow&x&\geq&\dfrac{15}{-3}\\ \\&\Leftrightarrow&x&\geq&-5\end{array}$

$S=[-5\;;\ +\infty[$
La solution est l'ensemble des rationnels $x$ supérieurs ou égaux à $-5.$
2)
$\begin{array}{rcrcl} -1>1-4x&\Leftrightarrow&1-4x&<&-1\\ \\&\Leftrightarrow&-4x&<&-1-1\\ \\&\Leftrightarrow&-4x&<&-2\\ \\&\Leftrightarrow&x&>&\dfrac{-2}{-4}\\ \\&\Leftrightarrow&x&>&\dfrac{1}{2}\end{array}$

$S=\left]\dfrac{1}{2}\;;\ +\infty\right[$
La solution est l'ensemble des rationnels $x$ supérieurs strictement à $\dfrac{1}{2}.$
b) Inéquation du type $ax+b\;\ast\; cx+d\ $ avec, $\ast\in\{>\;,\ <\;,\ \geq\;,\ \leq\}\;;\ a\neq c\;;\ a\neq 0\ $ et $\ c\neq 0$
Si $ax+b\;\ast\; cx+d$ alors, on a :
$\begin{array}{rcl} ax-cx&\ast&d-b\\ \\(a-c)x&\ast&d-b\\ \\x&\ast&\dfrac{d-b}{a-c}\end{array}$
Attention ! si $(a-c)$ est négatif, l'inégalité change de sens
Exemple
Résoudre dans $\mathbb{Q}\ :\ -2-7x>-5x-1$
Solution
$\begin{array}{rcrcl} -2-7x>-5x-1&\Leftrightarrow&5x-7x&>&2-1\\ \\&\Leftrightarrow&-2x&>&1\\ \\&\Leftrightarrow&x&<&\dfrac{1}{-2}\end{array}$
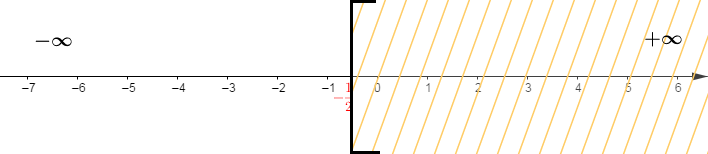
$S=\left]-\infty\;;\ \dfrac{1}{-2}\right[$
La solution est donc, l'ensemble des rationnels $x$ inférieurs strictement à $\dfrac{1}{-2}.$
Application 1
On donne les nombres : $\dfrac{2}{3}\;;\ -4\;;\ \dfrac{3}{5}\;;\ 2\ $ et $\ \dfrac{11}{3}$
Indiquer ceux qui sont des solutions pour chacune des inéquations suivantes :
a) $3x-4\geq 11$
b) $2x\leq 3x+4$
c) $-3x-5\geq x+3$
d) $4x-1\leq 3x$
Solution
a)
$\begin{array}{rcrcl} 3x-4\geq 11&\Leftrightarrow&3x&\geq&11+4\\ \\&\Leftrightarrow&3x&\geq&15\\ \\&\Leftrightarrow&x&\geq&\dfrac{15}{3}\\ \\&\Leftrightarrow&x&\geq&5\end{array}$
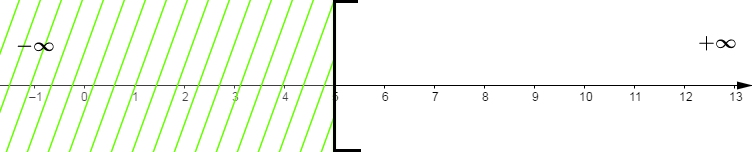
$S=[5\;;\ +\infty[$
On remarque que les valeurs $\dfrac{2}{3}\;;\ -4\;;\ \dfrac{3}{5}\;;\ 2\ $ et $\ \dfrac{11}{3}$ n'appartiennent pas à l'intervalle $[5\;;\ +\infty[.$
Par conséquent, aucune valeur donnée n'est solution de cette inéquation.
b)
$\begin{array}{rcrcl} 2x\leq 3x+4&\Leftrightarrow&2x-3x&\leq&4\\ \\&\Leftrightarrow&-x&\leq&4\\ \\&\Leftrightarrow&x&\geq&\dfrac{4}{-1}\\ \\&\Leftrightarrow&x&\geq&-4\end{array}$

$S=[-4\;;\ +\infty[$
Toutes les valeurs données sont supérieures ou égales à $-4$ donc, elles sont toutes solutions de l'inéquation $2x\leq 3x+4.$
c)
$\begin{array}{rcrcl} -3x-5\geq x+3&\Leftrightarrow&-3x-x&\geq&5+3\\ \\&\Leftrightarrow&-4x&\geq&8\\ \\&\Leftrightarrow&x&\leq&\dfrac{8}{-4}\\ \\&\Leftrightarrow&x&\leq&-2\end{array}$
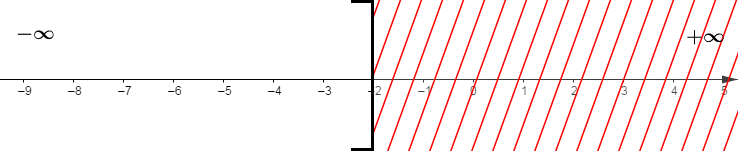
$S=]-\infty\;;\ -2]$
Parmi toutes les valeurs données seule $-4$ appartient à l'intervalle $]-\infty\;;\ -2].$
Par conséquent, $-4$ est la seule valeur solution de l'inéquation $-3x-5\geq x+3.$
d)
$\begin{array}{rcrcl} 4x-1\leq 3x&\Leftrightarrow&4x-3x&\leq&1\\ \\&\Leftrightarrow&x&\leq&1\end{array}$

$S=]-\infty\;;\ 1]$
On remarque que parmi les valeurs données, seules $\dfrac{2}{3}\;;\ -4\ $ et $\ \dfrac{3}{5}$ sont inférieures ou égales à $1.$
D'où, $\dfrac{2}{3}\;;\ -4\ $ et $\ \dfrac{3}{5}$ sont les seules valeurs solutions de l'inéquation $4x-1\leq 3x.$
Application 2
Résoudre chacune des inéquations suivantes.
Écrire sous forme de phrase la solution de chacune d'elle.
Donner deux nombres qui sont solutions et deux qui ne sont pas.
a) $3-4x<-9$
b) $x+3<-3x+5$
c) $3-2x>5-6x$
Solution
a)
$\begin{array}{rcrcl} 3-4x<-9&\Leftrightarrow&-4x&<&-3-9\\ \\&\Leftrightarrow&-4x&<&-12\\ \\&\Leftrightarrow&x&>&\dfrac{-12}{-4}\\ \\&\Leftrightarrow&x&>&3\end{array}$
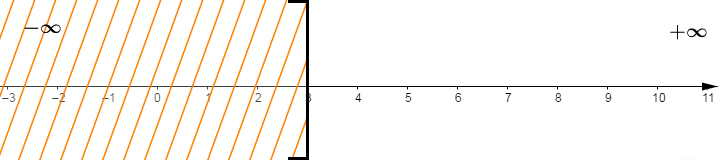
$S=]3\;;\ +\infty[$
Ainsi, la solution est l'ensemble des rationnels $x$ supérieurs strictement à $3.$
$4\ $ et $\ 5$ sont alors deux valeurs solutions de l'inéquation.
Par contre, $1\ $ et $\ 2$ sont deux valeurs qui ne sont pas solutions de l'inéquation.
b)
$\begin{array}{rcrcl} x+3<-3x+5&\Leftrightarrow&x+3x&<&-3+5\\ \\&\Leftrightarrow&4x&<&2\\ \\&\Leftrightarrow&x&<&\dfrac{2}{4}\\ \\&\Leftrightarrow&x&<&\dfrac{1}{2}\end{array}$
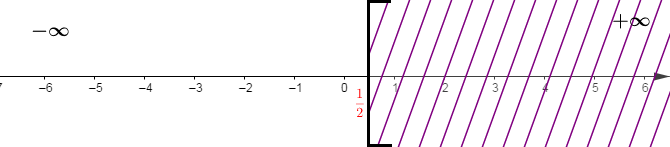
$S=\left]-\infty\;;\ \dfrac{1}{2}\right[$
La solution est l'ensemble des rationnels $x$ inférieurs strictement à $\dfrac{1}{2}.$
$-6\ $ et $\ -7$ sont deux valeurs solutions de l'inéquation.
$0.6\ $ et $\ 2$ sont deux valeurs non solutions de l'inéquation.
c)
$\begin{array}{rcrcl} 3-2x>5-6x&\Leftrightarrow&-2x+6x&>&-3+5\\ \\&\Leftrightarrow&4x&>&2\\ \\&\Leftrightarrow&x&>&\dfrac{2}{4}\\ \\&\Leftrightarrow&x&>&\dfrac{1}{2}\end{array}$

$S=\left]\dfrac{1}{2}\;;\ +\infty\right[$
La solution est l'ensemble des rationnels $x$ supérieurs strictement à $\dfrac{1}{2}.$
$0.6\ $ et $\ 10$ sont deux valeurs solutions de l'inéquation.
$0.4\ $ et $\ -21$ sont deux valeurs non solutions de l'inéquation.
II. Système de deux inéquations à une inconnue
Pour résoudre un système de deux inéquations à une inconnue :
$-\ $ On résout d'abord les deux inéquations indépendamment.
$-\ $ La solution du système est l'intersection des deux solutions des inéquations.
Exemple 1
Résoudre le système suivant :
$$\left\lbrace\begin{array}{rcl} x-5&>&-2\quad(1)\\ \\-2x+5&\leq&-5\quad(2)\end{array}\right.$$
Solution
En résolvant les deux inéquations indépendamment, on obtient :
$\begin{array}{rcrcl} (1)\quad x-5>-2&\Leftrightarrow&x&>&+5-2\\ \\&\Leftrightarrow&x&>&3\end{array}$
Donc, $S_{1}=]3\;;\ +\infty[$
$\begin{array}{rcrcl} (2)\quad -2x+5\leq -5&\Leftrightarrow&-2x&\leq&-5-5\\ \\&\Leftrightarrow&-2x&\leq&-10\\ \\&\Leftrightarrow&x&\geq&\dfrac{-10}{-2}\\ \\&\Leftrightarrow&x&\geq&5\end{array}$
D'où, $S_{2}=[5\;;\ +\infty[$
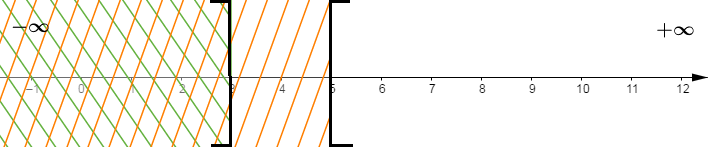
Finalement :
$$S=S_{1}\cap S_{2}=[5\;;\ +\infty[$$
La solution est l'ensemble des rationnels $x$ supérieurs ou égaux à $5.$
Exemple 2
Résoudre les systèmes d'inéquations suivants :
$1)\ \left\lbrace\begin{array}{rcl} x+3&>&4\\ \\-2x-4&\geq&6\end{array}\right.$
$2)\ \left\lbrace\begin{array}{rcr} -4x-8&>&8\\ \\7x&<&-7\end{array}\right.$
$3)\ \left\lbrace\begin{array}{rcr} 2x+3&\geq&-2\\ \\2x+3&\leq&2\end{array}\right.$
Solution
$1)\ \left\lbrace\begin{array}{rcl} x+3&>&4\quad(1)\\ \\-2x-4&\geq&6\quad(2)\end{array}\right.$
On résout d'abord les deux inéquations indépendamment. On a :
$\begin{array}{rcrcl} (1)\quad x+3>4&\Leftrightarrow&x&>&-3+4\\ \\&\Leftrightarrow&x&>&1\end{array}$
Donc, $S_{1}=]1\;;\ +\infty[$
$\begin{array}{rcrcl} (2)\quad -2x-4\geq 6&\Leftrightarrow&-2x&\geq&4+6\\ \\&\Leftrightarrow&-2x&\geq&10\\ \\&\Leftrightarrow&x&\leq&\dfrac{10}{-2}\\ \\&\Leftrightarrow&x&\leq&-5\end{array}$
Ainsi, $S_{2}=]-\infty\;;\ -5[$
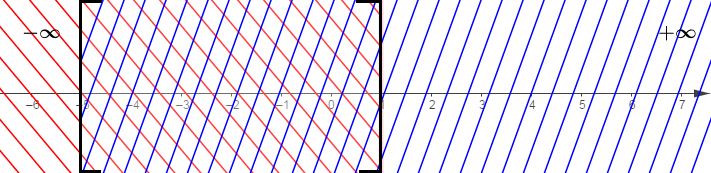
Par conséquent :
$$S=S_{1}\cap S_{2}=\emptyset$$
La solution est l'ensemble vide. Il n'existe donc pas de rationnels $x$ vérifiant simultanément les deux inéquations du système.
$2)\ \left\lbrace\begin{array}{rcr} -4x-8&>&8\quad(1)\\ \\7x&<&-7\quad(2)\end{array}\right.$
En résolvant les deux inéquations indépendamment, on obtient :
$\begin{array}{rcrcl} (1)\quad -4x-8>8&\Leftrightarrow&-4x&>&8+8\\ \\&\Leftrightarrow&-4x&>&16\\ \\&\Leftrightarrow&x&<&\dfrac{16}{-4}\\ \\&\Leftrightarrow&x&<&-4\end{array}$
Donc, $S_{1}=]-\infty\;;\ -4[$
$\begin{array}{rcrcl} (2)\quad 7x<-7&\Leftrightarrow&x&<&\dfrac{-7}{7}\\ \\&\Leftrightarrow&x&<&-1\end{array}$
D'où, $S_{2}=]-\infty\;;\ -1[$
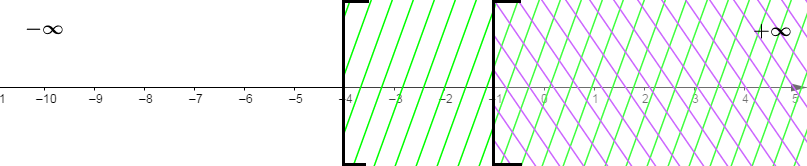
Finalement :
$$S=S_{1}\cap S_{2}=]-\infty\;;\ -4[$$
La solution est l'ensemble des rationnels $x$ inférieurs strictement à $-4.$
$3)\ \left\lbrace\begin{array}{rcr} 2x+3&\geq&-2\quad(1)\\ \\2x+3&\leq&2\quad(2)\end{array}\right.$
On résout d'abord les deux inéquations indépendamment. On obtient alors :
$\begin{array}{rcrcl} (1)\quad 2x+3\geq -2&\Leftrightarrow&2x&\geq&-3-2\\ \\&\Leftrightarrow&2x&\geq&-5\\ \\&\Leftrightarrow&x&\geq&\dfrac{-5}{2}\end{array}$
D'où, $S_{1}=\left[\dfrac{-5}{2}\;;\ +\infty\right[$
$\begin{array}{rcrcl} (2)\quad 2x+3\leq 2&\Leftrightarrow&2x&\leq&-3+2\\ \\&\Leftrightarrow&2x&\leq&-1\\ \\&\Leftrightarrow&x&\leq&\dfrac{-1}{2}\end{array}$
Ainsi, $S_{2}=\left]-\infty\;;\ \dfrac{-1}{2}\right]$
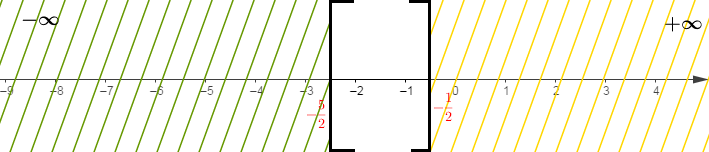
Par conséquent :
$$S=S_{1}\cap S_{2}=\left[\dfrac{-5}{2}\;;\ \dfrac{-1}{2}\right]$$
La solution est l'ensemble des rationnels $x$ compris entre $\dfrac{-5}{2}\ $ et $\ \dfrac{-1}{2}$
Auteur:
Mamadou Siradji Dia

Commentaires
NOUANI SHIBRAKI (non vérifié)
jeu, 05/27/2021 - 22:29
Permalien
Sunudaara est un site qui
Momo (non vérifié)
mer, 10/27/2021 - 09:12
Permalien
Très bon travail
Adja Tacko Mbodji (non vérifié)
lun, 02/13/2023 - 21:08
Permalien
Équation and inéquation
Jean Marc (non vérifié)
mar, 03/11/2025 - 22:18
Permalien
Je suis vraiment satisfait,
Ajouter un commentaire