La symétrie centrale

Classe:

Cinquième

I. Définition et notation

I.1. Activités

Marquer deux points

$A\$ et

$\ B$ et construire le point

$B$ tel que le point

$O$ soit le milieu de

$[AB].$

Comment sont les points

$A\ -\ O\ -\ B\ ?$

Compare

$OA\$ et

$\ OB$

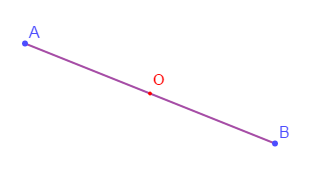
Les points

$A\ -\ O\ -\ B$ sont alignés.

Les distances

$OA\$ et

$\ OB$ sont égales.

On dit que le point

$A$ est le symétrique de

$B$ par rapport à

$O$ et que

$B$ est aussi le symétrique de

$A$ par rapport à

$O$ ou que

$A\$ et

$\ B$ sont symétriques par rapport à

$O.$

I.2. Définition

$A\$ et

$\ B$ sont symétriques par rapport à un point

$O$ signifie que

$O$ est le milieu du segment

$[AB].$

Le point

$O$ est appelé centre de symétrie, il est son propre symétrique par rapport à lui même.

I.3. Notation

Si

$A$ est le symétrique de

$B$ par rapport à

$O$ alors, on le note :

$A=S_{_{O}}[B]$

Si

$B$ est le symétrique de

$A$ par rapport à

$O$ alors, il se note :

$S_{_{O}}[A]=B$

II. Symétriques de figures simples et propriétés

II.1. Symétrique de trois points alignés

a) Activité

Marquer trois points

$R\;,\ S\;,\ T$ alignés. Construire un point

$O$ n'appartenant pas à la droite

$(RS).$

Construire les symétriques

$R'\;,\ S'\;,\ T'$ respectifs de

$R\;,\ S\;,\ T$ par rapport à

$O.$

Construire les symétriques

$R''\;,\ S''\;,\ T''$ respectifs de

$R\;,\ S\;,\ T$ par rapport à

$T.$

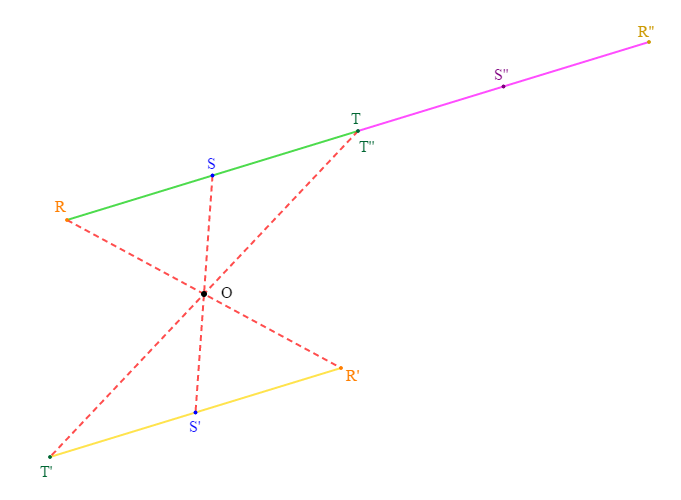
b) Propriétés

Les symétriques de trois points alignés sont aussi trois points alignés : on dit que la symétrie centrale conserve l'alignement.

II.2. Symétrique d'un segment

a) Activités

Trace un segment

$[AB]$ , marque le point

$O\notin[AB].$

Construire les points

$A'\;,\ B'$ symétriques de

$A\;,\ B$ par rapport à

$O.$

Compare les distances

$AB\$ et

$\ A'B'$

Construire les points

$A''\;,\ B''$ symétriques de

$A\;,\ B$ par rapport à

$A.$

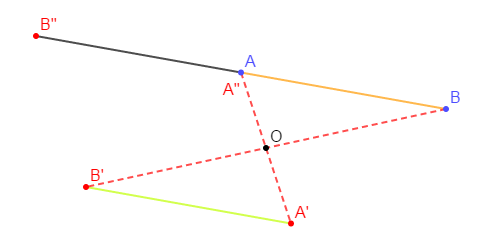
Les distances

$AB\$ et

$\ A'B'$ sont égales.

b) Propriétés

Le symétrique d'un segment est un segment de même longueur et qui lui est parallèle : on dit que la symétrie centrale conserve la longueur.

Application

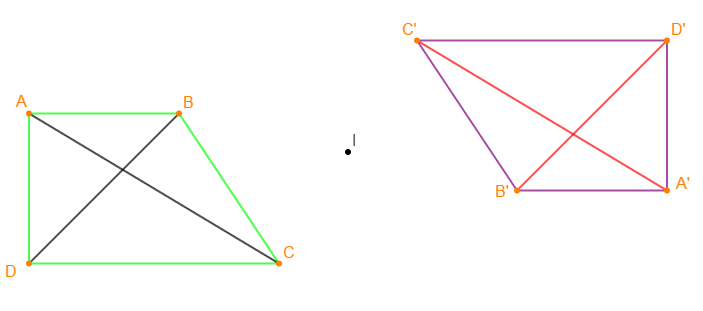
On considère la figure ci-après

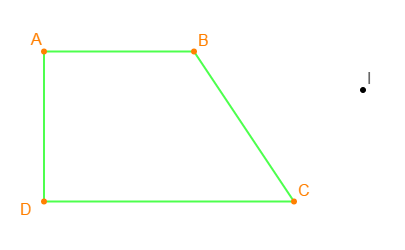
1) Construire les points

$A'\;,\ B'\;,\ C'\$ et

$\ D'$ symétriques respectifs des points

$A\;,\ B\;,\ C\$ et

$\ D$ par rapport à

$I.$

2) Justifier les affirmations suivantes :

$(A'B')\$ et

$\ (C'D')$ sont parallèles

$(A'C')\$ et

$\ (B'D')$ sont sécantes

Si la droite

$(A'B')$ est perpendiculaire à la droite

$(A'D')$ alors,

$(A'B')$ est parallèle à

$(D'C')$

$(A'C')\$ et

$\ (B'D')$ sont sécantes parce que

$(A'B')\$ et

$\ (C'D')$ sont parallèles.

$(A'B')//(C'D')\$ car

$\ (AB)//(CD)$

$(A'C')\$ et

$\ (B'D')$ sont sécantes parce que les diagonales

$(AC)\$ et

$\ (BD)$ sont sécantes.

II.3. Symétrique d'une demi-droite

a) Activités

Construis une demi-droite d'origine

$A$ , marque le point

$I$ n'appartenant pas à la demi-droite et

$B$ appartenant à la demi-droite.

Construire le symétrique de la demi-droite

$[AB)$ par rapport à

$I.$

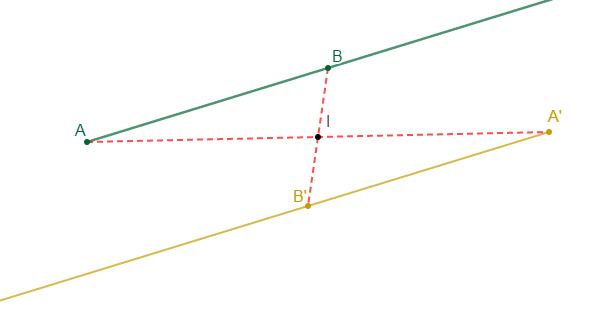
b) Propriétés

Le symétrique d'une demi-droite par rapport à un point est une demi-droite qui lui est parallèle et de sens opposé.

II.4. Symétrique d'une droite

a) Activités

Trace une droite

$(D)$ , marque un point

$I\notin(D).$

Construis

$(D')$ le symétrique de la droite

$(D)$ par rapport à

$I.$

Que constate-t-on ?

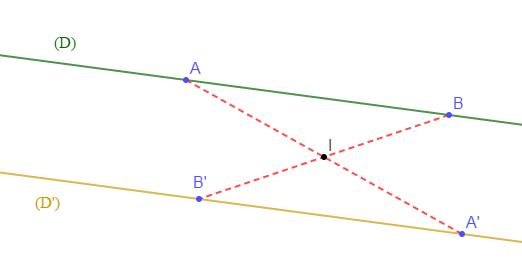
$S_{_{I}}[A]=A'\;,\quad S_{_{I}}[B]=B'$

On constate que

$(D)\$ et

$\ (D')$ sont parallèles

b) Propriétés

Le symétrique d'une droite par rapport à un point est une droite qui lui est parallèle.

II.5. Symétrique d'un triangle

a) Activités

Construis un triangle

$ABC$ et marque un point

$O$ n'appartenant pas au triangle.

Construis les symétriques

$A'\;,\ B'\;;\ C'$ respectifs de

$A\;,\ B\;;\ C$ par rapport à

$O.$

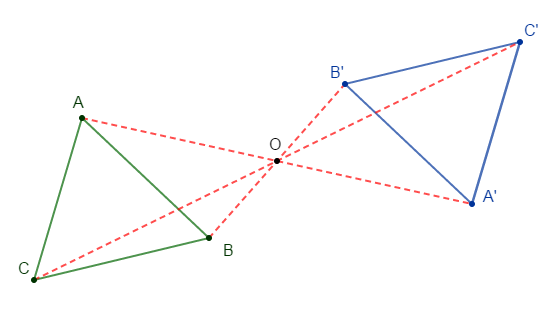
$S_{_{O}}(ABC)=A'B'C'$

$S_{_{O}}[A]=A'\;,\quad S_{_{O}}[B]=B'\;,\quad S_{_{O}}[C]=C'$

b) Propriétés

Le symétrique d'un triangle est un triangle de même nature.

II.6. Symétrique d'un cercle

a) Activités

Trace un cercle

$(\mathcal{C})$ de centre

$O$ et de rayon

$r=2,5\;cm.$

Marque les points

$I\;;\ J\;;\ K$ tels que :

$OI=2\;cm\;;\quad OJ=2,5\;cm\;;\quad OK=3\;cm$

Construire les symétriques

$(\mathcal{C}_{1})\;,\ (\mathcal{C}_{2})\;,\ (\mathcal{C}_{3})$ respectifs de

$(\mathcal{C})$ par rapport à

$I\;;\ J\;;\ K.$

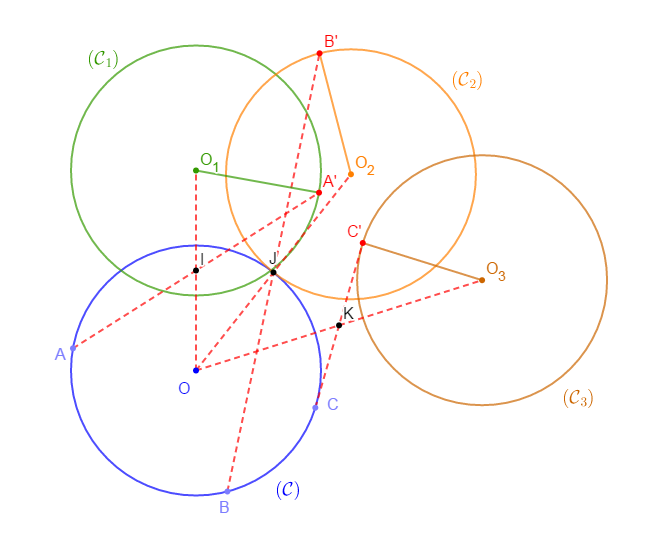
$S_{_{I}}(\mathcal{C})=(\mathcal{C}_{1})\;,\ S_{_{J}}(\mathcal{C})=(\mathcal{C}_{2})\;,\ S_{_{K}}(\mathcal{C})=(\mathcal{C}_{3})$

$S_{_{I}}[O]=O_{1}\;,\quad S_{_{J}}[O]=O_{2}\;,\quad S_{_{K}}[O]=O_{3}$

$S_{_{I}}[A]=A'\;,\quad S_{_{J}}[B]=B'\;,\quad S_{_{K}}[C]=C'$

b) Propriétés

Le symétrique d'un cercle par rapport à un point est un cercle de même rayon et dont le centre est le symétrique du centre du cercle considéré par rapport au point.

Auteur:

Mamadou Siradji Dia

Commentaires

Ibrahima sy (non vérifié)

mar, 01/05/2021 - 06:56

Permalien

Télécharger des documents

C'est très intéressant

répondre

Lamze (non vérifié)

sam, 01/23/2021 - 01:29

Permalien

Merci beaucoup à vous

répondre

mAX (non vérifié)

mar, 03/29/2022 - 15:00

Permalien

COURS

JE SUIS CONTENT

répondre

Mame bousso diop (non vérifié)

mer, 04/06/2022 - 00:05

Permalien

Le symétrique de droites

Le symétrique de droites perpendiculaires par rapport à une droite

répondre

landing badji (non vérifié)

jeu, 12/12/2024 - 16:34

Permalien

Appréciation

Merci pour ce cours bien détaillé

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

La symétrie centrale - 5e

Formulaire de recherche

I. Définition et notation

I.1. Activités

I.2. Définition

I.3. Notation

II. Symétriques de figures simples et propriétés

II.1. Symétrique de trois points alignés

a) Activité

b) Propriétés

II.2. Symétrique d'un segment

a) Activités

b) Propriétés

Application

II.3. Symétrique d'une demi-droite

a) Activités

b) Propriétés

II.4. Symétrique d'une droite

a) Activités

b) Propriétés

II.5. Symétrique d'un triangle

a) Activités

b) Propriétés

II.6. Symétrique d'un cercle

a) Activités

b) Propriétés

Commentaires

Télécharger des documents