Le Cercle - 6e
Classe:
Sixième
I. Présentation
Activité
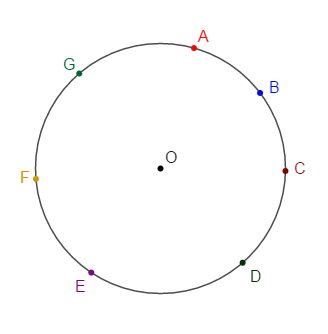
Soit un point $O$ du plan.
Placer les points $A\;,\ B\;,\ C\;,\ D\;,\ E\;,\ F\;,\ G$ distincts tels que :
$$OA=OB=OC=OD=OE=OF=OG=2.5\;cm$$
1) Quelle est la nature de la figure obtenue ?
2) Que représente $O$ pour la figure ?
3) Que représente la mesure $2.5\;cm$ pour la figure ?
Solution
1) Cette figure est une ligne fermée appelée cercle.
2) Le point $O$ est appelé centre de ce cercle.
3) La mesure $2.5\;cm$ est appelé rayon de ce cercle.
Définition
Un cercle est un ensemble de points situés à une même distance par rapport à un point appelé centre.
Notation
Le cercle $\mathcal{C}$ de centre $O$ et de rayon $r$ est noté : $$\mathcal{C}(O\;;\ r)$$
II. Vocabulaire
Activité
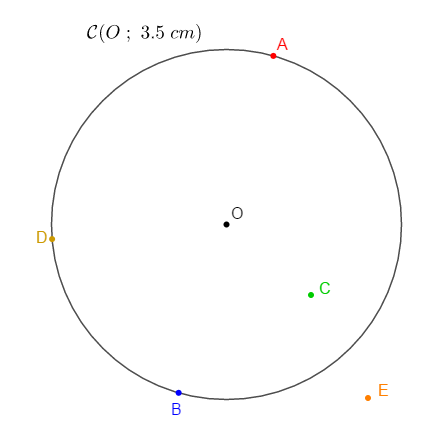
Soit un point $O$ du plan. Tracer le cercle $\mathcal{C}(O\;;\ 3.5\;cm).$
Marquer les points $A\;,\ B\;,\ C\;,\ D$ et $E$ tels que :
$\ -\ A\;,\ B\ $ et $\ D$ appartiennent à $\mathcal{C}\ $ et les points $A\;,\ B\;,\ O$ alignés ;
$\ -\ C$ et $E$ de part et d'autre de $\mathcal{C}$
1) Comparez $AO\ $ et $\ OB\;,\ AO+OB\ $ et $\ AB$
2) Comparez le rayon à $OD$ puis à $OC$ et enfin à $OE.$
Solution
1) On a : $AO=OB\ $ et $\ AO+OB=AB$ car $O$ est le milieu de $[AB].$
2) Soit $r$ le rayon du cercle. Comme $D\in\mathcal{C}(O\;;\ 3.5\;cm)$ alors, $OD=r.$
Aussi, on a : $OC<r\ $ et $\ OE>r$
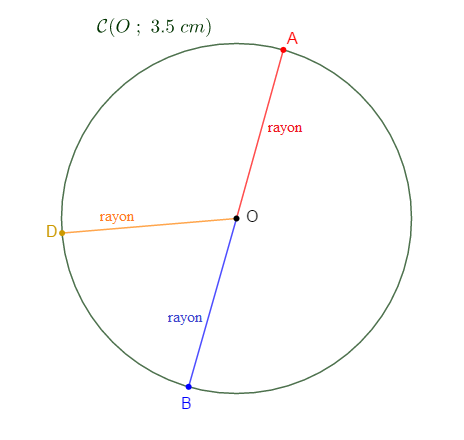
$\blacktriangleright\ $ Le rayon est la distance entre le centre du cercle et un point du cercle
Exemples : $OD\;,\ OA\;,\ OB$
$\blacktriangleright\ $ La corde est un segment dont les extrémités sont sur le cercle.
Exemples : $[AD]\;,\ [BD]\;,\ [AB]$
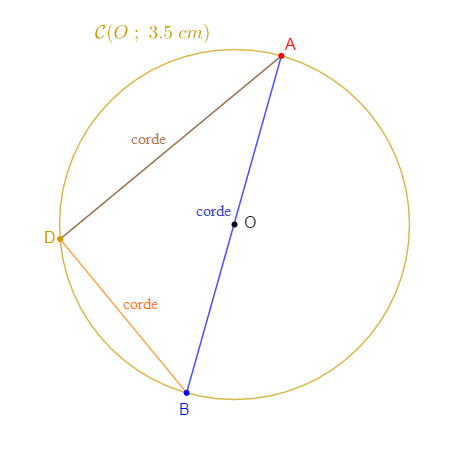
$\blacktriangleright\ $ Le diamètre est une corde qui passe par le centre du cercle.
Exemple : $AB$
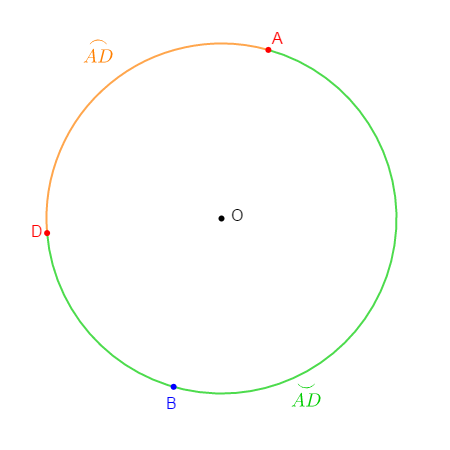
$\blacktriangleright\ $ L'arc est une partie délimitée par deux points.
Exemples
$\blacktriangleright\ $ l'arc délimité par $A$ et $B$ est noté $\overset{\displaystyle\frown}{AB}$
Pour L'arc délimité par $A$ et $D$ on a :
Le petit arc est appelé arc saillant ; on note $\overset{\displaystyle\frown}{AD}$
Le grand arc contenant le centre du cercle est appelé arc rentrant;on le note $\overset{\displaystyle\smile}{AD}$
$\blacktriangleright\ $ Intérieur d'un cercle :
Le point $C$ n'appartient pas au cercle et on : $CO<r$ ; alors $C$ est intérieur au cercle
$\blacktriangleright\ $ Extérieur d'un cercle :
Le point $E$ n'appartient pas au cercle et on a : $OE>r$ ; alors $E$ est extérieur au cercle
$\blacktriangleright\ $ Point du cercle : le point $D$ appartient au cercle et on a : $OD=r$ ; alors $D$ est un point du cercle
$\blacktriangleright\ $ Le périmètre d'un cercle est la circonférence de ce cercle
$$P=2\times\pi\times r=\mathrm{d}\times\pi$$
avec :
$\mathrm{d}=2\times r$
$r=\text{rayon}$
$\mathrm{d}=\text{diamètre}$
$\pi\approx 3.14$
$P=\text{périmètre}$
$\blacktriangleright\ $ L'aire d'un disque est la surface de la partie intérieure au cercle (disque)
$$A=r\times r\times\pi$$
avec :
$A=\text{aire ou surface}$
$r=\text{rayon}$
$\pi\approx 3.14$
III. Positions relatives de deux cercles
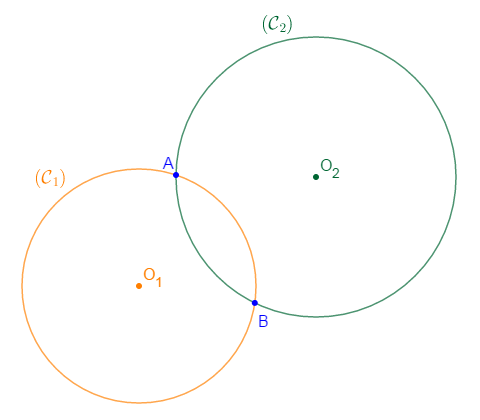
III.1. Cercles sécants
Deux cercles sont dits sécants lorsqu'ils ont deux points en communs.
Exemple
Soient $\mathcal{C}_{1}(O_{1}\;;\ r_{1})\ $ et $\ \mathcal{C}_{2}(O_{2}\;;\ r_{2})$ deux cercles sécants en $A$ et $B$
On a : $\mathcal{C}_{1}\cap \mathcal{C}_{2}=\{A\;;\ B\}$
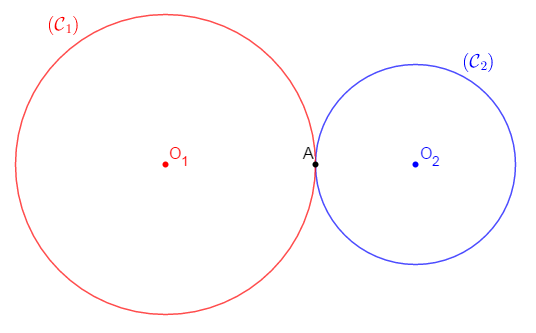
III.2. Cercles tangents
Deux cercles sont dits tangents lorsqu'ils ont un seul point en commun.
Exemple
Soient $\mathcal{C}_{1}(O_{1}\;;\ r_{1})\ $ et $\ \mathcal{C}_{2}(O_{2}\;;\ r_{2})$ deux cercles tangents en $A$
$1^{e}$ Cas : cercles tangents extérieurement
On a : $\mathcal{C}_{1}\cap \mathcal{C}_{2}=\{A\}$
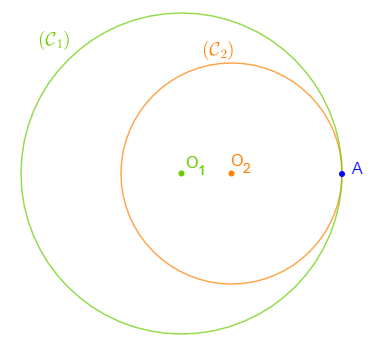
$2^{e}$ Cas : cercles tangents intérieurement
On a : $\mathcal{C}_{1}\cap \mathcal{C}_{2}=\{A\}$
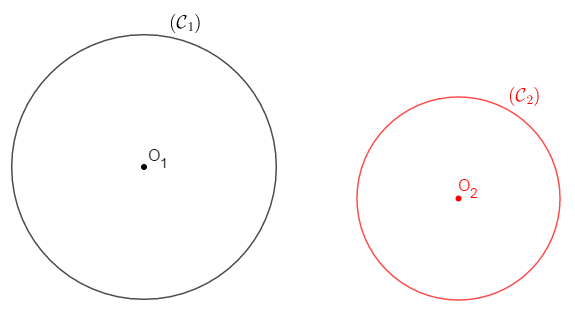
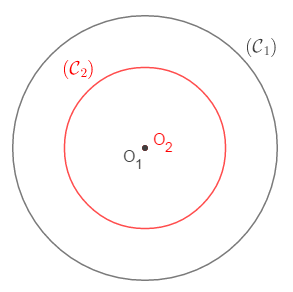
III.3. Cercles disjoints
Deux cercles sont dits disjoints lorsqu'ils n'ont aucun point en commun.
Exemple
Soient $\mathcal{C}_{1}(O_{1}\;;\ r_{1})\ $ et $\ \mathcal{C}_{2}(O_{2}\;;\ r_{2})$ deux cercles disjoints.
$1^{e}$ Cas : cercles disjoints extérieurement
On a : $\mathcal{C}_{1}\cap \mathcal{C}_{2}=\{\emptyset\}$
$2^{e}$ Cas : cercles disjoints intérieurement
On a : $\mathcal{C}_{1}\cap \mathcal{C}_{2}=\{\emptyset\}$
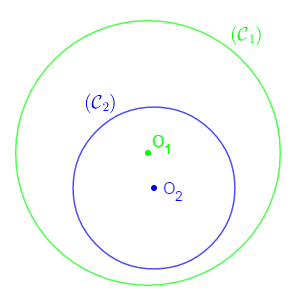
Remarque
Dans le cas particulier où $\mathcal{C}_{1}\ $ et $\ \mathcal{C}_{2}$ ont le même centre $(O=O')$, on dit que $\mathcal{C}_{1}\ $ et $\ \mathcal{C}_{2}$ sont concentriques.

Commentaires
ibrahima thiam (non vérifié)
mar, 10/09/2018 - 14:00
Permalien
appréciation
Idrissa Diallo (non vérifié)
dim, 10/27/2019 - 16:28
Permalien
Excellent cours
Anonyme (non vérifié)
mer, 12/08/2021 - 19:38
Permalien
mon dieu c'est super je like
Anonyme (non vérifié)
dim, 03/13/2022 - 17:04
Permalien
Intéressant
Ajouter un commentaire