Les systèmes d'équations et d'inéquations - 2nd
I. Système de deux équations à deux inconnues
ax+by &=& c\\
a'x+b'y &=& c'
\end{array}\right.\quad \text{où } \ a, \ b,\ c,\ a',\ b'\ \text{ et } c'\ \in\mathbb{R}$$
I.1 Méthodes de résolution
I.1.1 Méthode d'addition ou de combinaison
Soit à résoudre le système suivant $\left\lbrace\begin{array}{llll}
3x-4y &=& 5 & (1)\\
2x+3y &=& 6 & (2)
\end{array}\right.$
Nous avons choisi de chercher d'abord $x$.
Et donc, pour éliminer $y$, on multiplie l'équation (1) par 3 et l'équation (2) par 4 ensuite, on les additionne .
Le système devient $\left\lbrace\begin{array}{llll}
9x-12y &=& 15 & (3)\\
8x+12y &=& 24 & (4)
\end{array}\right.$
$(3)+(4)\ \Rightarrow\ 17x=39\;;\ $ soit $x=\dfrac{39}{17}$
Nous pouvons directement remplacer la valeur de $x$ dans l'une des équations (1) ou (2) pour trouver $y$.
On peut aussi répéter la procédure pour trouver $y$ en multipliant (1) par 2 et (2) par -3.
On obtient $\left\lbrace\begin{array}{llll}
6x-8y &=& 10 & (5)\\
-6x-9y &=& -18 & (6)
\end{array}\right.$
$(5)+(6)\ \Rightarrow\ -17y=-8\;;\ $ soit $y=\dfrac{8}{17}$
I.1.2 Méthode de substitution
I.1.3 Méthode de comparaison
x &=& \dfrac{5+4y}{3} & (3)\\
\\
x &=& \dfrac{6-3y}{2} & (4)
\end{array}\right.$$
En posant (3)=(4) on obtient :
Soit : $x=\dfrac{39}{17}$
I.1.4 Méthode de Cramer
ax+by &=& c\\
a'x+b'y &=& c'
\end{array}\right.\quad \text{où } \ a, \ b,\ c,\ a',\ b'\ \text{ et } c'\ \in\mathbb{R}$$
On calcul d'abord le déterminant de $(\mathbf{S})$. On a :
$det(\mathbf{S})=\Delta=\begin{vmatrix}
a & b\\
a' & b'
\end{vmatrix}=ab'-a'b$
Ensuite on pose $\Delta_{x}=\begin{vmatrix}
c & b\\
c' & b'
\end{vmatrix}=cb'-c'b\ $ et $\ \Delta_{y}=\begin{vmatrix}
a & c\\
a' & c'
\end{vmatrix}=ac'-a'c$
Enfin, selon le cas, on donne la solution
$\centerdot\ \ $ Si $\Delta\neq 0\ $ alors le système admet une solution unique $(x,\ y)\ $ où $$x=\dfrac{\Delta_{x}}{\Delta}\quad \text{et}\quad y=\dfrac{\Delta_{y}}{\Delta}$$
$\centerdot\ \ $ Si $\Delta=0\ $ et si, $\ \Delta_{x}=0\ $ et $\ \Delta_{y}=0$ alors le système admet une infinité de solutions $(x,\ y)\ $ qui vérifie $ax+by+c=0$ (ou $a'x+b'y+c'=0$)
$\centerdot\ \ $ Si $\Delta=0\ $ et si, $\ \Delta_{x}\neq 0\ $ ou $\ \Delta_{y}\neq 0$ alors le système n'a pas de solutions. $$S=\emptyset$$
I.2 Interprétation géométrique
ax+by &=& c\\
a'x+b'y &=& c'
\end{array}\right.\ $ qui devient $(\mathbf{S}')\ \left\lbrace\begin{array}{lll}
ax+by-c &=& 0\\
a'x+b'y-c' &=& 0
\end{array}\right.$
$\text{où } \ a, \ b,\ c,\ a',\ b'\ \text{ et } c'\ \in\mathbb{R}$
Considérons les droites $(\mathfrak{D_{1}})\ :\ ax+by-c=0\ $ et $\ (\mathfrak{D_{2}})\ :\ a'x+b'y-c'=0$
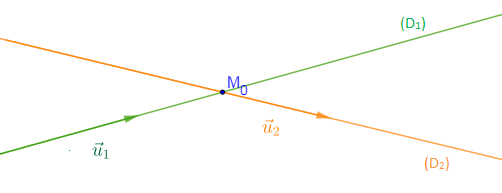
Résoudre le système revient à déterminer les points d'intersection des droites $(\mathfrak{D_{1}})\ $ et $\ (\mathfrak{D_{2}})$
-b\\
a
\end{pmatrix}\ $ vecteur directeur de $(\mathfrak{D_{1}})\ $ et $\ \vec{u}_{2}\begin{pmatrix}
-b'\\
a'
\end{pmatrix}\ $ vecteur directeur de $(\mathfrak{D_{2}})$
Si $(\mathfrak{D_{1}})\ $ est sécante à $\ (\mathfrak{D_{2}})$ alors $det(\vec{u}_{1};\ \vec{u}_{2})\neq 0$
$det(\vec{u}_{1};\ \vec{u}_{2})=\begin{vmatrix}
-b & -b'\\
a & a'
\end{vmatrix}=-a'b+ab'=det(\mathbf{S})$
$$S=\left\lbrace M_{0};\ \text{point d'intersection des droites }(\mathfrak{D_{1}})\ \text{ et }(\mathfrak{D_{2}})\right\rbrace$$
$2^{e}\ $ cas
Si $(\mathfrak{D_{1}})\parallel(\mathfrak{D_{2}})\ \text{ et }(\mathfrak{D_{1}})\cap(\mathfrak{D_{2}})=\emptyset$
$$S=\emptyset$$
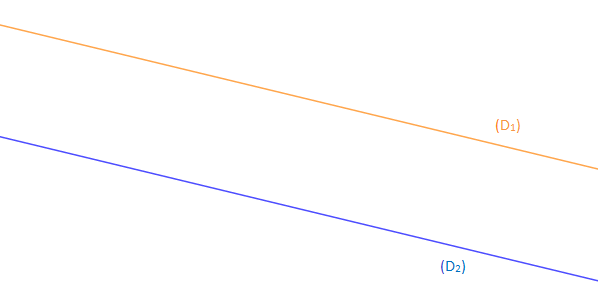
D'où, $$S=\emptyset$$
$3^{e}\ $ cas
Si $(\mathfrak{D_{1}})=(\mathfrak{D_{2}})$ alors les droites sont confondues.
$(\mathfrak{D_{1}})\parallel(\mathfrak{D_{2}})\ $ donc, $\ det(\vec{u}_{1};\ \vec{u}_{2})=det(\mathbf{S})=\Delta=0\ $ et on a : $\dfrac{a}{a'}=\dfrac{b}{b'}=\dfrac{c}{c'}$
Ainsi, $$S=\left\lbrace(x,\ y)\in\mathbb{R}^{2}/\;ax+by-c=0\right\rbrace\ \text{ ou }\ \left\lbrace(x,\ y)\in\mathbb{R}^{2}/\;a'x+b'y-c'=0\right\rbrace$$
II. Système d'inéquations à deux inconnues
2x-3 &\leq & 1&(1)\\
x+2y &\geq & -4&(2)
\end{array}\right.$$
Considérons les droites $(\mathfrak{D_{1}})\ :\ 2x-3=1\ \text{ soit }\ x=2$ et $\ (\mathfrak{D_{2}})\ :\ x+2y+4=0$
Dans un repère orthonormé $(O;\ \vec{i},\ \vec{j})$ on représente ces droites.
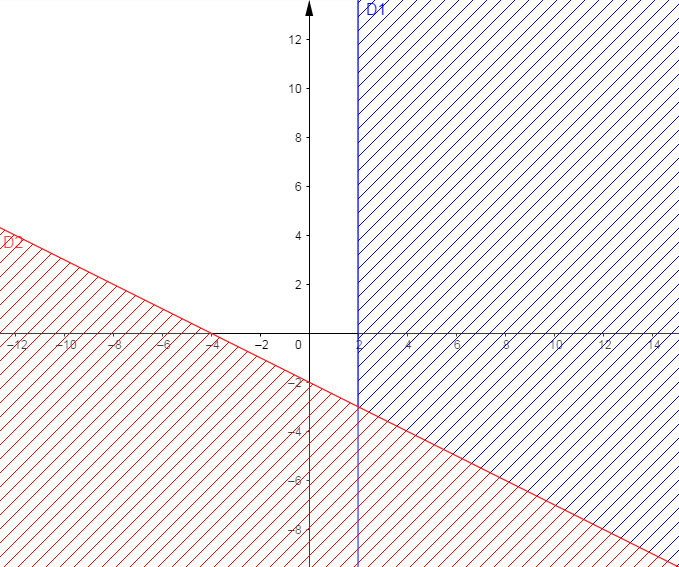
III. Programmation linéaire
Activité
Pour fabriquer un fauteuil il faut utiliser les machines $A$ et $B$ pendant une heure $(1h)\;,\ $ la machine $C$ pendant trois heures $(3h)$.
Pour fabriquer une chaise on utilise les machines $A$ et $C$ pendant une heure $(1h)\;,\ $ la machine $B$ pendant deux heures $(2h)$.
Mais les machines ne sont disponibles que soixante heures $(60h)$ pour $A\;,\ $ quatre vingts dix heures $(90h)$ pour $B$ et cent cinquante heures $(150h)$ pour $C$.
Un fauteuil génère un bénéfice de $10\,000\;F$ et une chaise $5\,000\;F.$
Combien faut-il fabriquer de fauteuils et de chaises pour obtenir, dans ces conditions, un bénéfice maximum ?
Résolution
Données
Contraintes
Résolution graphique de $(S)$
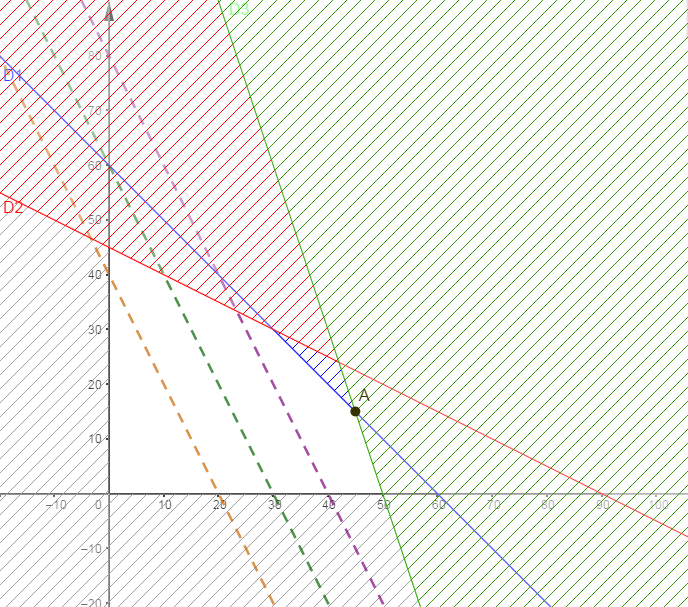
Soit $b_{B}=\dfrac{B}{5\,000}$ l'ordonnée à l'origine de $y=\dfrac{B}{5\,000}-2x$ alors si $B$ augmente $b_{B}$ aussi augmente.

Commentaires
Mbaye (non vérifié)
mer, 02/12/2020 - 10:38
Permalien
Bjr, je suis u jeune
Papa (non vérifié)
dim, 11/01/2020 - 14:22
Permalien
Je suis content de vous
Ajouter un commentaire