Série d'exercice sur les fonctions 1e S
Classe:
Première
Exercice 1
Dans chacun des cas suivants, déterminer l'ensemble de définition de la fonction $f $
$1)\quad\;f(x)=\sqrt{-x}\;;\qquad 2)\quad\;f(x)=\dfrac{1}{\sqrt{|x|}}\;;\qquad 3)\quad\;f(x)=\sqrt{1-x}$
$4)\quad\;f(x)=\dfrac{2x}{\sqrt{3x+7}}\;;\qquad 5)\quad\;f(x)=\dfrac{\sqrt{2x-5}}{x-3}$
$6)\quad\;f(x)=\sqrt{|-x|}\;;\qquad 7)\quad\;f(x)=\dfrac{1-\sqrt{-x}}{1+\sqrt{-x}}$
$8)\quad\;f(x)=\dfrac{2x-3}{6x^{2}-13x-5}\;;\qquad 9)\quad\;f(x)=\dfrac{2x-3}{6x^{2}-|13x-5|}$
$10)\quad\;f(x)=\dfrac{1}{\sqrt{6x^{2}-13x-5}}\;;\qquad 11)\quad\;f(x)=\dfrac{3x-6}{|x+1|-|x-5|}$
$12)\quad\;f(x)=\dfrac{\sqrt{-6x^{2}+13x+5}}{2x-3}\;;\qquad 13)\quad\;f(x)=\dfrac{\sqrt{-6x^{2}+13x+5}} {\sqrt{2x-3}}$
$14)\quad\;;f(x)=\sqrt{\dfrac{-6x^{2}+13x+5}{2x-3}}$
$$15)\quad\left\lbrace\begin{array}{lllll} f(x) &=& \dfrac{1}{x} &\text{si} & x\leq 1 \\ f(x) &=& x+3 &\text{si} & x>1 \end{array}\right.\qquad 16)\quad\left\lbrace\begin{array}{lllll} f(x) &=& \sqrt{3x^{2}-14x-5} & \text{si} & x\leq 1 \\ \\ f(x) &=& \dfrac{1}{\sqrt{-2^{2}+11x-15}} & \text{si}& x>1 \end{array}\right.$$
$17) \quad f(x)=\dfrac{(x-1)\sqrt{(1+x)(2-x)}}{x(2x-1)}$
Exercice 2
Pour chacune des fonctions numériques définies ci-dessous, préciser l'ensemble de définition suivant les valeurs du paramètre réel $m$
$1)\quad\;f(x)=\dfrac{3}{|x|+m}\;;\qquad 2)\quad\;f(x)=\dfrac{x^{2}-16}{x^{2}-mx+1}$
$3)\quad\;f(x)=\sqrt{x^{2}+m}\;;\qquad 4)\quad\;f(x)=\sqrt{x^{2}-mx+1}$
Exercice 3
Parmi les fonctions suivantes, préciser celles qui sont des applications :
$\text{f :}\ \mathbb{R}\rightarrow\mathbb{R}\quad\;x\mapsto |x|\;;\qquad \text{g :}\ \mathbb{R}\rightarrow\mathbb{R}\quad\;x\mapsto x-\sqrt{x}$
$\text{h :}\ [2\;;\ +\infty[\rightarrow\mathbb{R}\quad\;x\mapsto\sqrt{x-2}\;;\qquad\text{i :}\ [0\;;+\infty[\rightarrow\mathbb{R}\quad\;x\mapsto\dfrac{1}{x-1}$
$\text{j :}\ [0\;;+\infty[\rightarrow\mathbb{R}\quad\;x\mapsto\dfrac{x+1}{x^{2}+2x-3}\;;\qquad \text{k :}\ [0\;;+\infty[\rightarrow\mathbb{R}\quad\;x\mapsto\left|\dfrac{x}{x-1}\right|$
$\text{l :}\ [0\;;\ 0]\rightarrow\mathbb{R}\quad\;x\mapsto\dfrac{1}{\sqrt{4-x^{2}}}\;;\qquad \text{m :}\ ]-\infty\;;\ 0[\rightarrow\mathbb{R}\quad\;x\mapsto\dfrac{x-1}{x-3}$
Exercice 4
Parmi les fonctions suivantes, préciser celles qui définissent une bijection .Dans ce cas, déterminer la bijection réciproque.
$f_{1}\ :\ \mathbb{R}\rightarrow\mathbb{R}\quad\;x\mapsto 1-x\;;\qquad f_{2}\ :\ \mathbb{R}\rightarrow\mathbb{R}\quad\;x\mapsto 1+x^{2}$
$f_{3}\ :\ \mathbb{R}\rightarrow\mathbb{R}\quad\;x\mapsto\dfrac{1}{x}\;;\qquad f_{4}\ :\ \mathbb{R}_{-}\rightarrow\mathbb{R}_{+}\quad\;x\mapsto\sqrt{-x}$
$f_{5}\ :\ [0\;;\ 1]\rightarrow[0\;;\ 1]\quad\;x\mapsto 1-x\;;\qquad f_{6}\ :\ [4\;;\ +\infty[\rightarrow\mathbb{R}_{-}\quad\;x\mapsto -\sqrt{x-4}$
$f_{7}\ :\ \mathbb{R}_{-}\rightarrow]-\infty\;;\ 5]\quad\;x\mapsto -x^{2}+5\;;\qquad f_{8}\ :\ [2\;;\ +\infty[\rightarrow[3\;;\ +\infty[\quad\;x\mapsto 3+\sqrt{x-2}$
$ f_{9}\ :\ \mathbb{R}\setminus\{1\}\rightarrow\mathbb{R}\setminus\{-1\}\quad\;x\mapsto\dfrac{x+1}{x-1}$
Exercice 5
Dans chacun des cas suivants, étudier si l'application $f$ de $E$ vers $F$ est injective, surjective ou bijective.
$1)\quad E=F=\mathbb{R}\;,\ f(x)=x^{2}+2\;;\qquad 2)\quad E=\mathbb{R}\setminus\{1\}\;,\ F=\mathbb{R}\;,\ f(x)=\dfrac{1}{1-x}$
$3)\quad E=\mathbb{R}\setminus\{1\}\;,\quad F=\mathbb{R}\setminus\{2\}\;,\ f(x)=\dfrac{2x+1}{x-1}\;;\qquad 4)\quad E=\mathbb{R}_{+}\;,\ F=\mathbb{R}\;,\ f(x)=3x^{2}-4$
$5)\quad E=\mathbb{R}\;,\ F=[-3\;;\ +\infty[\;,\ f(x)=2x^{2}-3$
$6)\quad E=F=\mathbb{Z}\;,\ \text{si }x\text{ est pair :}\ f(x)=x-1\;,\text{ si }x\text{ est impair :}\ f(x)=x+1$
$7)\quad E=F=\mathbb{Z}\;,\text{ si }x\text{ est pair :}\ f(x)=\dfrac{x}{2}\;,\text{ si }x\text{ est impair :}\ f(x)=\dfrac{x-1}{2}$
$8)\quad E=F=\mathbb{Z}\;,\text{ si }x\text{ est pair :}\ f(x)=2x\;,\text{ si }x\text{ est impair :}\ f(x)=2x+1$
Exercice 6
Soit $f$ la fonction définie par : $f(x)=\dfrac{1+\sqrt{x^{2}-1}}{1-\sqrt{x^{2}-1}}$
1) Déterminer son ensemble de définition $D$
2) Résoudre dans $\mathbb{R}$ l'équation $f(x)=y$, où $y$ est un paramètre réel.
L'application $f\ :\ D\rightarrow\mathbb{R}$ est-elle injective ? surjective ?
3) Déterminer deux parties $E$ et $F$ de $\mathbb{R}$, les plus grandes possibles, pour que l'application $g\ :\ E\rightarrow F\quad\;x\mapsto f(x)$ soit bijective.
Définir alors $g^{-}$.
Exercice 7
Soit $f\ :\ \mathbb{R}\rightarrow\mathbb{R}\quad\;x\mapsto 2x+3$
1) Calculer $f(-\dfrac{1}{2})$ et $f(\dfrac{1}{2})$
2) Démontrer que $f$ est bijective et déterminer l'application réciproque.
3) La restriction de $f$ à $\mathbb{Z}$ est-elle une bijection de $\mathbb{Z}$ vers $\mathbb{Z}$ ?
\begin{eqnarray} \text{Soit }g\ :\ \mathbb{Z}\rightarrow \mathbb{Z}\ x &\mapsto& g(x)=\dfrac{x}{2}+4\;,\text{ si }x\text{ est pair} \nonumber \\ x &\mapsto& g(x)=\dfrac{x^{2}-x}{2}\;,\text{ si }x\text{ est impair } \nonumber \end{eqnarray}
Déterminer l'image par $g$ de chacun des entiers $(-2)\;,\ (-1)\;,\ 1\;,\ 2\;,\ 3.$
L'application $g$ est-elle injective ? surjective ?
Exercice 8
Le plan est rapporté au repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$
Soit le point $A(-1\;;\ 0)$ et le point $B(1\;;\ 0)$ et $\mathcal{C}$ le cercle de diamètre $[AB]$
Le demi-cercle fermé inclus dans $\mathcal{C}$ et formé des points de $\mathcal{C}$ d'ordonnées positives est appelé $\mathcal{C}_{1}.$
Le demi-cercle fermé inclus dans $\mathcal{C}$ et formé des points de $\mathcal{C}$ d'ordonnées négatives est appelé $\mathcal{C}_{2}.$
La droite $\mathcal{D}(O\;,\ \vec{i})$ est appelée $x'x$ (axe des abscisses).
Étant donné un point $M$ du cercle $\mathcal{C}$, on peut effectuer la construction suivante : par $M$, on trace la perpendiculaire à $x'x$ qui coupe $x'x$ en un point $H$ unique.
1) L'application :
\begin{eqnarray} f_{1}\ :\ \mathcal{C}_{1} &\rightarrow& x'x \nonumber \\ M &\mapsto& H \nonumber \end{eqnarray}
est-elle injective, surjective, bijective ?
2) Même question pour les applications suivantes :
\begin{eqnarray} f_{2}\ :\ \mathcal{C}_{2} &\rightarrow& [AB]\nonumber \\ M &\mapsto& H \nonumber \end{eqnarray}
\begin{eqnarray} f_{3}\ :\ \mathcal{C}_{3} &\rightarrow& [Ax) \nonumber \\ M &\mapsto& H \nonumber \end{eqnarray}
\begin{eqnarray} f_{4}\ :\ \mathcal{C}_{4} &\rightarrow& [AB] \nonumber \\ M &\mapsto& H \nonumber \end{eqnarray}
Exercice 9
La courbe $\mathcal{C}$ ci-dessous est la représentation graphique d'une fonction $f$ définie sur l'intervalle $[-6\;;\ 7]$
FIG...
1) Quelles sont les images des réels $3\;,\ -2\;,\ -6$ et $0$ par $f$ ?
2) Quels sont les antécédents de 2 ?
3) Résoudre graphiquement l'équation $f(x)=0.$
4) Quel est en fonction de $m$ le nombre de solutions de l'équation $f(x)=m$ ?
5) Résoudre graphiquement l'inéquation $f(x)>0$
6) Résoudre graphiquement l'inéquation $f(x)<2$
Exercice 10
Soit la courbe $\mathcal{C}$ ci-dessous, représentative de la fonction $f\ :\ x\rightarrow x^{3}-4x^{2}+3$, et la droite $\mathcal{D}$ d'équation $y=-x-3.$
1) Résoudre graphiquement l'équation $f(x)=3$, puis l'inéquation $f(x)<3.$
2) Résoudre graphiquement l'équation $f(x)=0$, puis l'inéquation $f(x)\geq 0.$
On donnera un encadrement d'amplitude $5\times 10^{-1}$ des solutions non entières.
3) Résoudre graphiquement l'équation $f(x)=-x-3$, puis l'inéquation $f(x)\leq -x-3$
4) Retrouver algébriquement les résultats des questions 1), 2) et 3)
FIG...2
Exercice 11
Les courbes suivantes sont sont-elles représentatives de fonctions ?
FIG...3
Exercice 12
Soit $f$ une fonction numérique définie sur l'intervalle $[-a\;;\ +a]$ avec $a>0.$
Soient $g$ et $h$ les fonctions telles que :
$g(x)=\dfrac{1}{2}[f(x)+f(-x)]\;;\qquad h(x)=\dfrac{1}{2}[f(x)-f(-x)]$
1) Démontrer que $g$ est une fonction paire et que $h$ est une fonction impaire.
2) Vérifier que $f=g+h$.
3) Déterminer $g$ et $h$ lorsque $f(x)=x^{2}+x+1$ ; lorsque $f(x)=\dfrac{2x+3}{x+2}$ lorsque $f(x)=\dfrac{x^{2}+3x-2}{x^{2}+x+1}$
Exercice 13
Soient $f$ et $g$ deux fonctions affines telles que : $f(x)=ax+b$ ; $g(x)=cx+d.$
1) Trouver une relation entre $a\;,\ b\;,\ c$, et $d$ caractérisant la propriété : $f\circ g=g\circ f$.
2) Soient $\mathcal{D}$ et $\mathcal{D'}$ les droites d'équations $y=ax+b$ et $y=cx+d.$
On désigne par $\Delta$ la droite d'équation $y=x$ . Montrer que $f\circ g=g\circ f$ équivaut à :
(1) $\mathcal{D}$ et $\mathcal{D'}$ est égale à $\Delta$,soit
(2) $\mathcal{D}$ et $\mathcal{D'}$ sont strictement parallèles à $\Delta$,soit
(3) $\mathcal{D}$, $\mathcal{D'}$ et $\Delta$ sont concourantes.
Exercice 14
1) Soient $f\;,\ g$ et $h$ les fonctions définies par :
$f(x)=x^{2}\;;\qquad g(x)=\dfrac{1}{1+x}\;;\qquad h(x)=x-1$
a) Déterminer les fonctions $(g\circ f)$ et $(h\circ g).$
b) Montrer que les fonctions $[(h\circ g)\circ f]$ et $[h\circ(g\circ f)]$ ont même ensemble de définition $D$ puis que pour tout $x$ de $D$, on a : $[(h\circ g)\circ f](x)=[h\circ(g\circ f)](x).$
N.B On peut donc écrire sans ambiguïté : $(h\circ g\circ f)(x)$
2) Soient $f\;,\ g$ et $h$ les fonctions définies par :
$f(x)=3x\;;\qquad g(x)=1+x^{2}\;;\qquad h(x)=\sqrt{x}$
Déterminer et comparer les fonctions $(f\circ g\circ h)$ et $(h\circ g\circ f)$
Exercice 15
Soit $f$ telle que $f(x)=|x+2|+|x-2|+2x.$
1) Exprimer $f(x)=$ sans valeur absolue suivant les valeurs de $x.$
2) Tracer $\mathcal{C}$ courbe représentative de la fonction $f.$
3) Résoudre graphiquement les équations $f(x)=2$ et $f(x)=x$
Exercice 16
Dans chacun des cas suivants, on demande de tracer la courbe $\mathcal{C}$ représentative de la fonction $f$ relativement à un repère orthogonal $(O\;,\ \vec{i}\;,\ \vec{j})$
1) On sait que :
a) $f$ est impaire
b) si $x\in\;[0\;;\ 4]\;,\text{ alors } f(x)=x\;;\text{ si }\;x\in\;]4\;;\ +\infty[\;,\text{ alors } f(x)=2$
2) On sait que :
a) $f$ est paire
b) si $x\in\;[0\;;\ 3[\;,\text{ alors } f(x)=2\;;\text{ si }x\in\;[3\;;\ +\infty[\;,\text{ alors } f(x)=\dfrac{1}{2}x+\dfrac{1}{2}$
3) On sait que :
a) $f$ est périodique, de période 2
b) si $x\in\;[0\;;\ 2[\;,\text{ alors } f(x)=-x+1$
Tracer $\mathcal{C}$ sur l'intervalle $[-4\;;\ 8[$.
4) On sait que :
a) $f$ est impaire
b) $f$ est périodique, de période 2
c) si $x\in\;[0\;;\ 1[\;,\text{ alors } f(x)=x$
Tracer $\mathcal{C}$ sur l'intervalle $]-1\;;\ 1[$ puis sur l'intervalle $]-3\;;\ 5[$
Connaît-on la valeur de $f(-1)$ ? de $f(3)$ ?
5) On sait que :
a) $f$ est paire
b) $f$ est périodique, de période 2
c) si $x\in\;[0\;;\ 1]\;,\text{ alors } f(x)=x$
Tracer $\mathcal{C}$ sur l'intervalle $[-5\;;\ 5]$
Exercice 17
Soit $f$ et $g$ deux fonctions définies sur un même intervalle $I$.
1) On suppose les deux fonctions $f$ et $g$ croissantes sur $I$.
Étudier le sens de variation de la somme $f+g$ sur $I$.
2) Reprendre la question pour deux fonctions $f$ et $g$ décroissantes sur $I$.
Exercice 18
Soit $f$ une fonction définie sur un intervalle $I$ et $g$ une fonction définie sur un intervalle $J$ contenant l'image par $f$ de l'intervalle $I$.
1) On suppose les deux fonctions $f$ et $g$ croissantes sur leur intervalle de définition
Étudier le sens de variation de la composée $f\circ g$ sur $I$.
2) On suppose les deux fonctions $f$ et $g$ décroissantes sur leur intervalle de définition.
Étudier le sens de variation de la composée $f\circ g$ sur $I$.
3) On suppose $f$ croissante sur $I$ et $g$ décroissantes sur $J$.
Étudier le sens de variation de la composée $f\circ g$ sur $I$
Exercice 19
Soit $f$ une fonction numérique définie sur l'intervalle $[-a\;;\ a]$ avec $a>0$.
1) Si $f$ est paire et strictement croissante sur $[0\;;\ a]$, déterminer le sens de variation de $f$ sur $[-a\;;\ 0].$
2) Si $f$ est impaire et strictement croissante sur $[0\;;\ a]$, déterminer le sens de variation de $f$ sur $[-a\;;\ 0].$
Étudier et représenter graphiquement la restriction à $[-1\;;\ 5]$ de la fonction $f$ définie par :
$f(x)=\dfrac{E(3-x)}{E(x)}$
Étudier et représenter graphiquement la fonction $f$ définie par : $f(x)=\dfrac{1}{E(x+E(-x))}$
Étudier le sens de variation des fonctions suivantes :
$f\ :\ x\rightarrow x\;;\qquad g\ :\ x\rightarrow \sqrt{x}\;;\qquad h\ :\ x\rightarrow\dfrac{1}{x}$
$k\ :\ x\rightarrow x^{2}\;;\qquad m\ :\ x\rightarrow ax+b\;;\qquad n\ :\ x\rightarrow ax^{2}+bx+c$
Exercice 20
Soit $k$ un réel strictement positif et $f$ une fonction définie sur $\mathbb{R}$ telle que, pour tout réel $x$, $f(x+k)=-f(x-k).$
Montrer que la fonction $f$ est périodique de période $4k$
Exercice 21
Soit $f$ une fonction définie sur $\mathbb{R}$, telle que, pour tout réel $x$, $f(x+1)=\dfrac{1+f(x)}{1-f(x)}$
1) Calculer $f(x+2)\;,\ f(x+3)$ et $f(x+4)$
2) Que peut-on en déduire pour la fonction $f$
Exercice 22
On considère la fonction $f$ de $\mathbb{R}$ dans $\mathbb{R}$ définie par :
$x\rightarrow f(x)=E(x)-2E\left(\dfrac{x}{2}\right)$
1) Donner, sans employer le symbole $\mathbb{E}$, les expressions de $f(x)$ sur le segment $[0\;;\ 2]$
2) Montrer que $f(x)$ est périodique et construire sa représentation graphique dans le plan rapporté au repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$
Exercice 23
$n$ étant un entier donné supérieur ou égal à 1, on considère la fonction $f$ définie sur $[0\;;\ +\infty[$ par :
$f(x)=x-n\;E\left(\dfrac{x}{n}\right)$
Démontrer que cette fonction est périodique.
En déduire que, quel que soit $x\geq 0$, on a $0\leq f(x)<n$
Exercice 24
On considère les fonctions $f\ :\ \mathbb{R}\rightarrow \mathbb{R}\quad\;x\mapsto 3x-5\;;\qquad g\ :\ \mathbb{R}\rightarrow \mathbb{R}\quad\;x\mapsto \dfrac{2x^{2}+1}{x^{2}+1}$
1) Démontrer que $\forall x\in\;\mathbb{R}\;,\ 1\leq g(x)<2$
2) La fonction $f$ est-elle bornée sur $\mathbb{R}$ ?
3) Démontrer que la fonction $(g\circ f)$ existe bornée sur $\mathbb{R}$
4) Démontrer que la fonction $(f\circ g)$ est bornée sur $\mathbb{R}$ et que :
$$\forall x\in\;\mathbb{R}\;,\ -2\leq (f\circ g)(x)<1$$
Exercice 25
On donne les fonctions $f\;,\ g\;,\ h$ de $\mathbb{R}$ vers $\mathbb{R}$ telles que :
$f(x)=\dfrac{x^{3}}{|x|}+1\;;\qquad g(x)=\dfrac{x-1}{|x|-1}\;;\qquad h(x)=|2x+1|-|x-3|+4$
Déterminer les restrictions :
1) de $f$ à $\mathbb{R}_{-}^{\ast}$, à $[-1\;;\ 1]\setminus\{0\}$
2) de $g$ à $\mathbb{R}^{+}\setminus\{1\}$, à $\mathbb{R}^{-}\setminus\{1\}$
3) de $h$ à $\left]-\infty\;;\ -\dfrac{1}{2}\right]$, à $\left[-\dfrac{1}{2}\;;\ 3\right]$ et à $[3\;;\ +\infty[$
Exercice 26
Pour tout réel $x$, on définit $E(x)$ (partie entière de $x$) comme étant le plus grand entier inférieur ou égal à $x$, c'est-à-dire l'unique entier $n$ tel que : $n\leq x<n+1$
Soit les fonctions $\Phi\ :\ \mathbb{R}\rightarrow [0\;;\ 1],\quad\;x\mapsto x-E(x)$ et $h\ :\ [0\;;\ 1]\rightarrow [0\;;\ 1],\quad\;u\mapsto |2u-1|$
1) Soit $f=h\circ \Phi$ . Montrer que $f$ est une fonction paire, périodique de période 1.
2) Soit $F$ la restriction de $f$ à $[0\;;\ \dfrac{1}{2}]$
Démontrer que $F$ admet une fonction réciproque $F^{-1}$, dont on précisera l'ensemble de définition et l'ensemble image
3) Soit $g=F^{-1}\circ f$ .Démontrer que $g$ est une fonction paire, définie sur $\mathbb{R}$, périodique de période 1.
Soit $k\in\;\mathbb{Z}$. Dans les deux cas suivants, exprimer $g(x)$ en fonction de $x$ et $k$ :
$\text{a)}\quad\;x\in\;[k\;;\ k+\dfrac{1}{2}[\qquad \text{b)}\quad\;x\in\;[k-\dfrac{1}{2}\;;\ k[$
Exercice 27
1) a) $f$ et $g$ sont deux fonctions positives croissantes sur un intervalle $I$
Montrer que la fonction $p=f g$ est croissante sur $I$
b) $f$ et $g$ sont deux fonctions positives décroissantes sur un intervalle $I$
Montrer que la fonction $p=f g$ est décroissante sur $I$
2) $f$ est une fonction définie sur un intervalle $I$ et garde un signe constant sur $I$
($f>0$ sur $I$ ou bien $f<0$ sur $I$) On suppose $f$ monotone sur $I$
En examinant tous les cas possibles, trouver le sens de variation de la fonction $\dfrac{1}{f}$ sur $I$
Applications :
Trouver le sens de variation de chacune des fonctions suivantes sur l'intervalle $I$
$\text{a) }\;x\rightarrow x\sqrt{x+3}\ I=[1\;;\ +\infty[\;;\qquad\text{b) }\;x\rightarrow \dfrac{1}{x^{2}+1}\ I=[0\;;\ +\infty[$
$\text{c) }\;x\rightarrow\dfrac{1}{\sqrt{x}}\ I=]0\;;\ +\infty[\;;\qquad\text{d) }\;x\rightarrow |x|(x^{2}+1)\ I=]-\infty\;;\ 0]\text{ puis }I=[0\;;\ +\infty[$
Exercice 28
Soient $f_{a\;,\ b}\;,\ g\;,\ h$ les trois fonctions numériques suivantes :
$f_{a\;,\ b}\ :\ x\mapsto ax+b\;;\qquad g\ :\ x\mapsto\dfrac{1}{x}\;;\qquad h\ :\ x\mapsto x^{2}$
Montrer que les fonctions $\Phi$ suivantes peuvent s'écrire comme composées de $f_{a\;,\ b}\;,\ g\;,\ h$ en choisissant convenablement $a$ et $b$
$1)\ \Phi\ :\ x\mapsto\dfrac{2}{x-1}+3\qquad 2)\ \Phi\ :\ x\mapsto\dfrac{3}{(3x-2)^{2}}\qquad 3)\ \Phi\ :\ x\mapsto (2x-1)^{2}+2$
$4)\ \Phi\ :\ x\mapsto\dfrac{x+1}{x}\qquad 5)\ \Phi\ :\ x\mapsto x^{4}-4\qquad 6)\ \Phi\ :\ x\mapsto x^{2}+2x-3$
Exercice 29
Partie entière et partie décimale
Pour tout réel $x$, on admet qu'il existe un unique entier relatif $n$ tel que $n\leq x<n+1$
Cet entier est appelé "partie entière de $x$" et est noté $E(x)$.
Par exemple $2\leq 2.8<3$ donc $E(2.8)=2$.
Ainsi $E(x)=n$ signifie que $x\in\;[n\;;\ n+1[$ ou encore que $n\leq x<n+1$.
A Étude de la fonction $E$
1) Placer sur un axe les nombres suivants et en déduire leur partie entière :
$1.75\;;\ -3.4\;;\ \dfrac{3}{2}\;;\ \dfrac{17}{4}\;;\ \sqrt{2}\;;\ 5\;;\ -3\;;\ \sqrt{2}-2\;;\ 1-2\sqrt{3}\;;\ 0.245\;;\ \pi\;;\ -\dfrac{\pi}{2}$
2) Quels sont les nombres $x$ tels que :
a) $E(x)=3$ ?
b) $E(x)=-2$ ?
c) $E(x)=0$ ?
3) Étudier la fonction $E$ et tracer la courbe représentative de $E$ restreinte à l'intervalle $[-5\;;\ 4]$.
4) Quels sont les nombres $x$ tels que :
a) $E(2x)=3$ ?
b) $E\left(\dfrac{1}{5}x\right)=-1$ ?
c) $E(3x-2)=4$ ?
d) $E\left(\dfrac{1}{x}\right)=1(x\neq 0)$ ?
e) $E(x^{2})=3$ ?
5) $x$ est un réel tel que $E(x)=4$.
Montrer qu'alors $E(x+3)=7$.
Montrer que, plus généralement, si $x$ est un réel quelconque et $p$ un entier relatif quelconque, alors $E(x+p)=E(x)+p$.
B Avec la partie entière
$h$ est la fonction définie sur $]0\;;\ +\infty[$ par $h(x)=\dfrac{1}{x}$
$f$ désigne la fonction $E\circ h$.
1) Quel est l'ensemble de définition de $f$ ?
2) Calculer $f(1)\;,\ f(3.2)$, puis $f(x)$ lorsque $x>1$.
3) Calculer $f\left(\dfrac{1}{2}\right)\;,\ f(0.75)$, puis $f(x)$ lorsque $x\in\;\left]\dfrac{1}{2}\;;\ 1\right[$
4) $p$ est un entier naturel non nul.
Calculer $f(x)$ pour $x\in\;\left]\dfrac{1}{p+1}\;;\ \dfrac{1}{p}\right]$
5) Tracer la représentation graphique de la restriction de $f$ à $\left[\dfrac{1}{4}\;;\ +\infty\right[$
6) Peut-on tracer la courbe représentative de $f$ sur $]0\;;\ +\infty[$ ?
C La partie décimale
$d$ est la fonction définie sur $\mathbb{R}$ par $d(x)=x-E(x)$.
1) Calculer les images par $d$ des réels :
$5.2\;;\ \dfrac{3}{2}\;;\ 8\;;\ -5\;;\ -6.3$
2) Donner au moins cinq réels différents, et pas tous de même signe, qui vérifient : $d(x)=0.3$
3) Montrer que pour tout réel $x$, $0\leq d(x)<1$.
4) Montrer que $d$ est périodique.
5) Tracer la représentation graphique de la restriction de $d$ à $[0\;;\ 1[$ et en déduire alors la courbe représentative de $d$.
6) On considère la fonction $g$ définie sur $]0\;;\ +\infty$ par $g(x)=\dfrac{d(x)}{\sqrt{x}}$
Calculer $g(x)$ pour $x\in\;]0\;;\ 1[$.
En déduire une majoration de $g(x)$ sur $]0\;;\ 1[$.
Montrer alors que $g$ est bornée sur $]0\;;\ +\infty[$.
Exercice 30
Le plan est rapporté au repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$
Soit le point $A(-1\;;\ 0)$ et le point $B(1\;;\ 0)\text{ et }\mathcal{C}$ le cercle de diamètre $[AB].$
Le demi-cercle fermé inclus dans $\mathcal{C}$ et formé des points de $\mathcal{C}$ d'ordonnées positives est appelé $\mathcal{C_{1}}.$
Le demi-cercle fermé inclus dans $\mathcal{C}$ et formé des points de $\mathcal{C}$ d'ordonnées négatives est appelé $\mathcal{C_{2}}.$
La droite $\mathcal{D}(O\;,\ \vec{i})$ est appelée $x'x$ (axe des abscisses).
Étant donné un point $M$ du cercle $\mathcal{C}$ , on peut effectuer la construction suivante :
par $M$ , on trace la perpendiculaire à $x'x$ qui coupe $x'x$ en un point $H$ unique.
1) L'application
\begin{eqnarray} f_{1}\ :\ \mathcal{C_{1}} &\rightarrow & x' x\nonumber\\ M &\mapsto & H\nonumber \end{eqnarray} est-elle injective, surjective, bijective ?
2) Même question pour les applications suivantes :
\begin{eqnarray} f_{2}\ :\ \mathcal{C_{2}} &\rightarrow & [AB]\nonumber\\ M &\mapsto & H\nonumber \end{eqnarray}
\begin{eqnarray} f_{3}\ :\ \mathcal{C_{3}} &\rightarrow & [A x)\nonumber\\ M &\mapsto & H\nonumber \end{eqnarray}
\begin{eqnarray} f_{4}\ :\ \mathcal{C_{4}} &\rightarrow & [AB]\nonumber\\ M &\mapsto & H\nonumber \end{eqnarray}
Exercice 31
La courbe $\mathcal{C}$ ci-dessous est la représentation graphique d'une fonction $f$ définie sur l'intervalle $[-6\;;\ 7].$
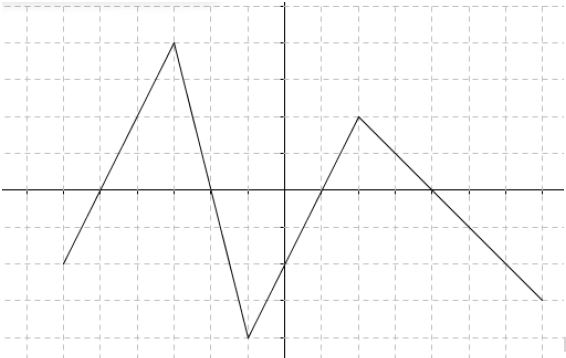
1) Quelles sont les images des réels $3\;,\ -2\;,\ -6\text{ et }0\text{ par }f$ ?
2) Quels sont les antécédents de 2 ?
3) Résoudre graphiquement l'équation $f(x)=0.$
4) Quel est en fonction de $m$ le nombre de solutions de l'équation $f(x)=m$ ?
5) Résoudre graphiquement l'inéquation $f(x)>0.$
6) Résoudre graphiquement l'inéquation $f(x)<2.$
Exercice 32
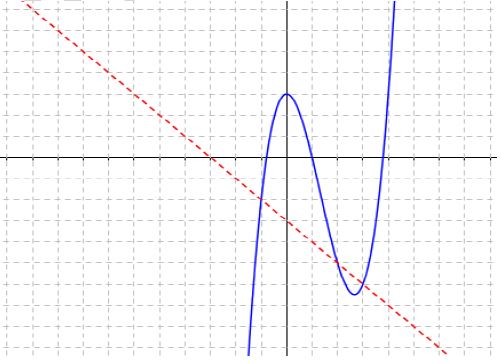
Soit la courbe $\mathcal{C}$ ci-dessous, représentative de la fonction $f\ :\ x\mapsto x^{3}-4x^{2}+3$, et la droite $\mathcal{D}$ d'équation $y=-x-3.$
1) Résoudre graphiquement l'équation $f(x)=3$, puis l'inéquation $f(x)<3.$
2) Résoudre graphiquement l'équation $f(x)=0$, puis l'inéquation $f(x)\geq 0.$
On donnera un encadrement d'amplitude $5\times 10^{-1}$ des solutions non entières.
3) Résoudre graphiquement l'équation $f(x)=-x-3$ , puis l'inéquation $f(x)\leq -x-3.$
4) Retrouver algébriquement les résultats des questions 1), 2) et 3).
Exercice 33
Les courbes suivantes sont-elles représentatives de fonctions ?
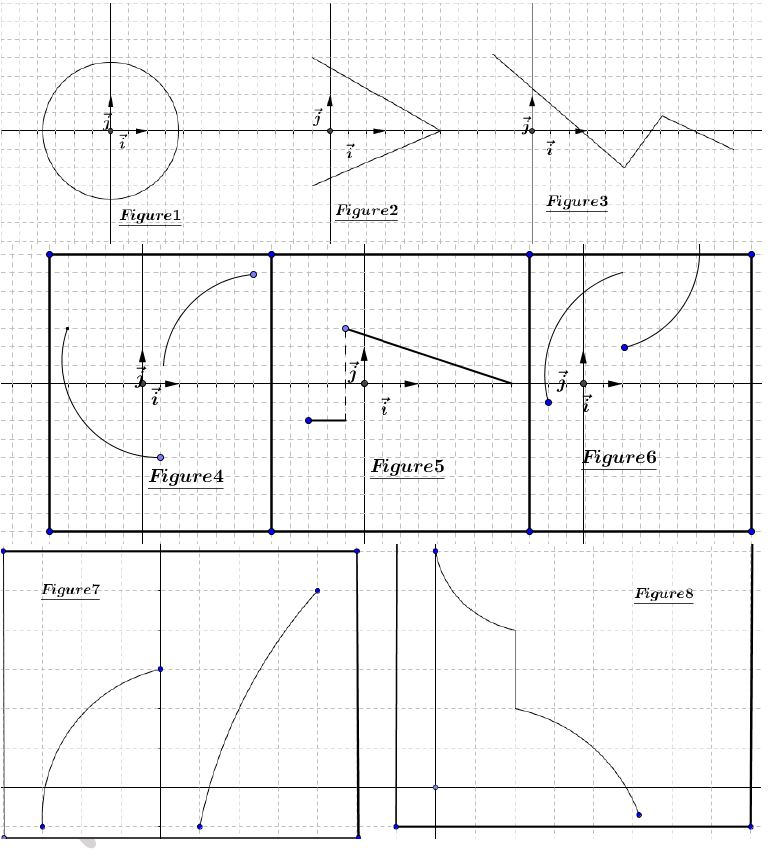
Exercice 34
Soit $f\ :\ \mathbb{R}\rightarrow \mathbb{R}\text{ avec }f(x)=\dfrac{x-1}{x+2}\text{ si }x\neq -2\text{ et }f(-2)=1\;,\text{ et }g\ :\ \mathbb{R}\rightarrow\mathbb{R}\ x\rightarrow 2x+3$
1) Déterminer les fonctions $f+g\;,\ fg\;,\ \dfrac{f}{g}\;,\ 3f-2g.$
2) Déterminer et comparer les fonctions $(g\circ f)\text { et }(f\circ g ).$
Exercice 35
Les courbes suivantes sont représentatives de fonctions :
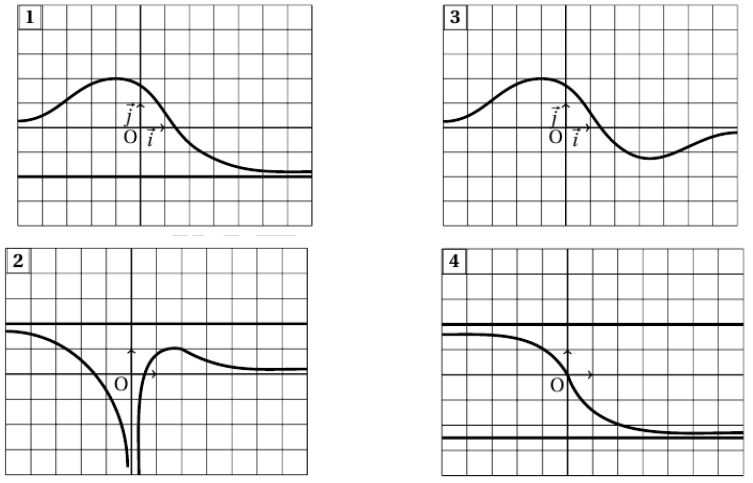
Dans chacun des cas, dire si la fonction admet : un maximum, un minimum, un majorant et/ou un minorant.
Préciser leurs valeurs s'ils existent.
Exercice 36
Dans chacun des cas suivants, $f$ est une fonction définie sur $\mathbb{R}\text{ et }\mathcal{C}$ sa courbe représentative.
A l'aide de la courbe, conjecturer l'existence d'un majorant et d'un minorant (entiers) pour $f$, puis démontrer cette conjecture algébriquement.
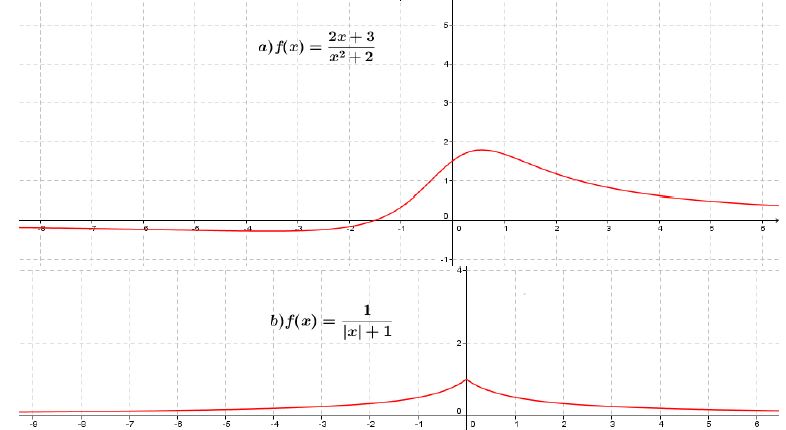
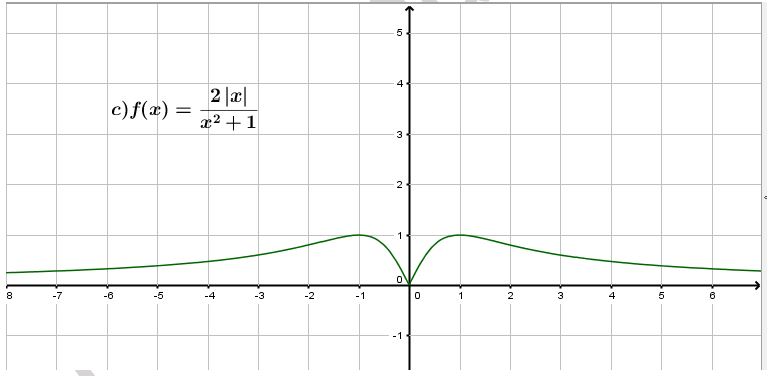
Exercice 37
Les courbes ci-dessous sont les représentations graphiques de fonctions périodiques.
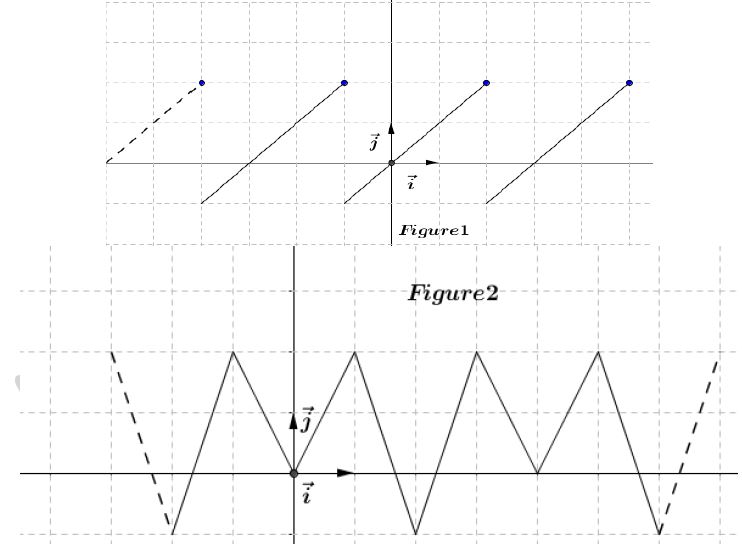
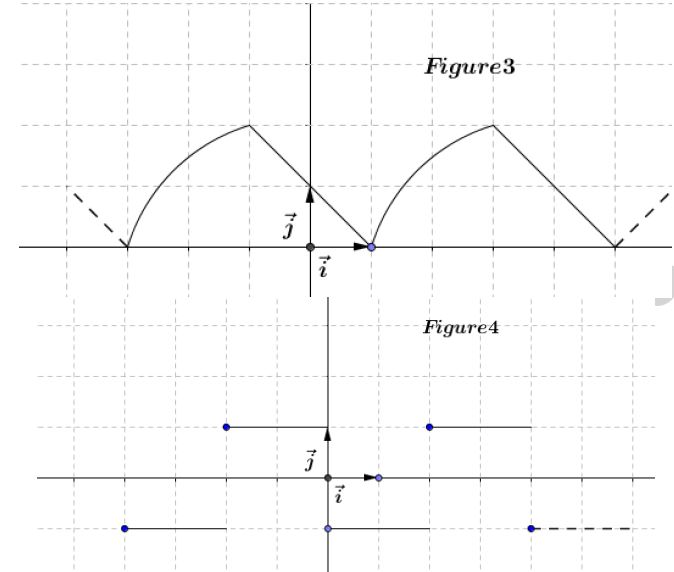
Quelles sont les périodes de ces fonctions ?
Exercice 38
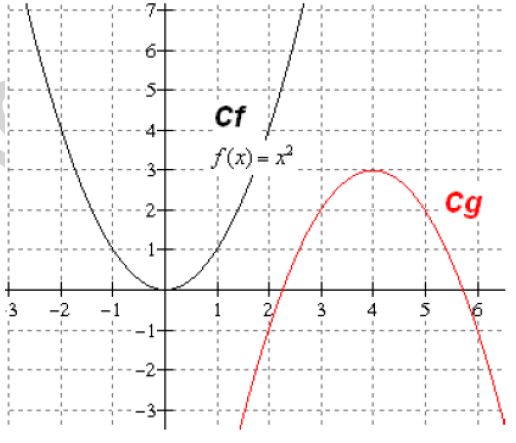
Dans un même repère $(O\;;\ \vec{i}\;;\ \vec{j})$, on a représenté la courbe $\mathcal{C_{f}}$ de la fonction $f$ définie par $f(x)=x^{2}$ ainsi que la courbe $\mathcal{C_{g}}$ d'une fonction $g.$
En vous aidant des transformations permettant de fabriquer $\mathcal{C_{g}}$ à partir de $\mathcal{C_{f}}$, donner l'expression de $g(x)$

Commentaires
Anonyme (non vérifié)
ven, 04/23/2021 - 19:12
Permalien
merci c'est très intéressant
HAwa sow (non vérifié)
dim, 12/03/2023 - 20:35
Permalien
Réussite en s
Anonyme (non vérifié)
dim, 02/12/2023 - 10:11
Permalien
Vos exercices sont trés
Ngom (non vérifié)
mer, 02/22/2023 - 09:22
Permalien
Bien
HAwa sow (non vérifié)
dim, 12/03/2023 - 20:36
Permalien
Les corrections des exercices
HAwa sow (non vérifié)
dim, 12/03/2023 - 20:37
Permalien
Correction des exercices svp
Anonyme (non vérifié)
mar, 09/03/2024 - 13:16
Permalien
La correction s'il vous plaît
Mouhamadou pam (non vérifié)
mar, 01/14/2025 - 22:07
Permalien
Vous aimez trop les
Ajouter un commentaire