Vous êtes ici

Série d'exercices : Angles - Trigonométrie - 2nd

Classe:

Seconde

Exercice 1

1) Déterminer la mesure principale de :

$\dfrac{25\pi}{3}\;,\ \dfrac{77\pi}{4}\;,\ -\dfrac{81\pi}{5}$

2) Donner les valeurs exactes de :

$\text{a)}\ \cos\dfrac{2\pi}{3}\;,\ \sin\dfrac{2\pi}{3}\;,\ \cos\dfrac{25\pi}{4}\;,\ \sin\dfrac{25\pi}{4}\;,\ \sin\dfrac{7\pi}{4}\;,\ \sin\dfrac{213\pi}{6}\;,\ \cos\dfrac{-77\pi}{3}$

b) $\tan\left(\dfrac{7\pi}{6}\right)\;,\ \tan\left(\dfrac{3\pi}{4}\right)\;,\ \tan\left(\dfrac{-5\pi}{6}\right)$

Exercice 2

Transformer les expression suivantes :

$A=3\cos(-x)+2\sin\left(\dfrac{\pi}{2}-x\right)+4\sin x+\cos x$

$B=2\sin\left(\dfrac{\pi}{2}+x\right)+5\cos(\pi-x)-3\sin(-x)-\cos x$

$C=-\sin(\pi-x)+\cos\left(\dfrac{\pi}{2}+x\right)-\sin(\pi-x)$

$D=\sin\left(\dfrac{\pi}{2}+x\right)+\cos(x-\pi)+\sin\left(x+\dfrac{3\pi}{2}\right)+\cos(x+\pi)$

$E=2\cos\left(\dfrac{3\pi}{2}-\pi+x\right)-2\sin(x-2\pi)+5\sin\left(\dfrac{5\pi}{2}+x\right)$

Exercice 3

Établissez les égalités suivantes :

$1)\ \cos^{2}x-\sin^{2}x=2\cos^{2}x-1=1-2\sin^{2}x$

$2)\ \cos^{4}x+\sin^{4}x=1-2\cos^{2}x\sin^{2}x$

$3)\ (\cos x+\sin x)^{2}+(\cos x-\sin x)^{2}=2$

Exercice 4

Donner la longueur d'un demi-cercle de rayon $2\;cm$, et d'un quart de cercle de rayon $4\;cm.$

Exercice 5

1) Compléter le tableau suivant, où $l$ désigne la longueur de l'arc de cercle de rayon $R$, intercepté par l'angle $\alpha$ mesuré en degrés : $$\begin{array}{|c|c|c|c|c|c|}\hline l& & &\pi R/4& &2\pi R/5 \\ \hline\alpha&60&120& &30& \\ \hline\end{array}$$

2) Compléter le tableau suivant, où $l$ désigne la longueur de l'arc de cercle de rayon $R$, intercepté par l'angle $\alpha$ mesuré en radians : $$\begin{array}{|c|c|c|c|c|c|}\hline l& & &\pi R/6& &5\pi R/8 \\ \hline\alpha&2\pi&1& &2\pi/3& \\ \hline\end{array}$$

Exercice 6

On considère la figure suivante :

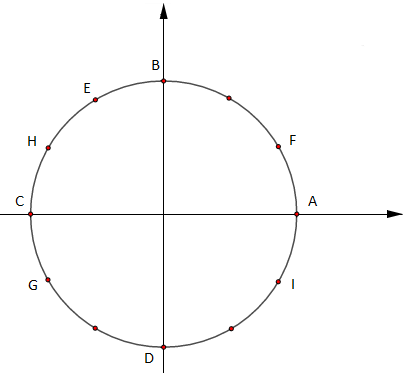
1) Parmi les réels suivants, quels sont ceux qui sont une abscisse curviligne du point $E$ ?

$\dfrac{4\pi}{12}\;;\ \dfrac{4\pi}{3}\;;\ -\dfrac{4\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{5\pi}{3}$

2) Quels sont les points du cercle trigonométrique qui ont pour abscisse curviligne les réels suivants :

$\dfrac{3\pi}{2}\;;\ \pi\;;\ \dfrac{\pi}{6}\;;\ \dfrac{5\pi}{6}\;;\ -\dfrac{7\pi}{6}\;;\ \dfrac{11\pi}{6}$

Exercice 7

Donner un moyen géométrique de placer sur le cercle trigonométrique les points d'abscisses curvilignes :

$\dfrac{\pi}{3}\;;\ -\dfrac{\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{\pi}{6}\;;\ -\dfrac{\pi}{6}\;;\ \dfrac{5\pi}{6}$

Exercice 8

Placer sur le cercle trigonométrique les points d'abscisses curvilignes :

a) $\dfrac{\pi}{3}+\dfrac{k\pi}{2}\ ;$
$\quad$
b) $\dfrac{\pi}{6}+k\pi\ ;$
$\quad$
c) $-\dfrac{\pi}{3}+\dfrac{k\pi}{2}\ ;$
$\quad$
d) $\dfrac{\pi}{4}+k\pi\;,\ k$ entier relatif

Exercice 9

Placer sur le cercle trigonométrique les points d'abscisses curvilignes :

a) $100\pi\ ;$
$\quad$
b) $71\pi\ ;$
$\quad$
c) $-\dfrac{37\pi}{2}\ ;$
$\quad$
d) $\dfrac{18\pi}{4}$

Exercice 10

Compléter le tableau suivant : $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline ^{\circ}&45&30&60&15&18&75&135& & & & \\ \hline\text{rad}& & & & & & & &\pi/2&\pi/3&\pi/5&\pi/8 \\ \hline ^{\circ}&120&150&180&90& & & & & & &225 \\ \hline\text{rad}& & & & &\pi/6&\pi/4&2\pi/3&\pi/10&5\pi/6&\pi& \\ \hline\end{array}$$

Exercice 11

Pour chacune des mesures suivantes, on demande :

$-\ $ la mesure principale (en degré ou en radian, selon le cas) ;

$-\ $ la mesure dans $[0\;;\ 2\pi[$ (ou dans $[0^{\circ}\;;\ 360^{\circ}[$);

$-\ $ la mesure dans $]-2\pi\;;\ 0[$ (ou dans $[-360^{\circ}\;;\ 0^{\circ}[$).

1) $\dfrac{2008\pi}{3}\ ;$
$\quad$
2) $\dfrac{28\pi}{5}\ ;$
$\quad$
3) $\dfrac{27\pi}{4}\ ;$
$\quad$
4) $-\dfrac{19\pi}{3}\ ;$
$\quad$
5) $-270^{\circ}$

$\quad$

6) $-18\pi\ ;$
$\quad$
7) $1440^{\circ}\ ;$
$\quad$
8) $-2530^{\circ}\ ;$
$\quad$
9) $-\dfrac{\pi}{4}\ ;$
$\quad$
10) $\dfrac{5\pi}{6}$

$\quad$

11) $\dfrac{12\pi}{5}\ ;$
$\quad$
12) $-\dfrac{23\pi}{6}\ ;$
$\quad$
13) $210^{\circ}\ ;$
$\quad$
14) $-375^{\circ}\ ;$
$\quad$
15) $-4512^{\circ}\ ;$
$\quad$
16) $17\pi$

Exercice 12

On considère un triangle $ABC$ rectangle en $C$ et tel que $(\overrightarrow{AB}\;,\ \overrightarrow{AC})=35^{\circ}.$

Soit $O$ et $A'$ les milieux respectifs des côtés $[AB]$ et $[BC].$ Trouver la mesure principale des angles orientés :

$(\overrightarrow{OB}\;,\ \overrightarrow{OA}')\;;\ (\overrightarrow{OC}\;,\ \overrightarrow{OA}')\;;\ (\overrightarrow{OA}'\;,\ \overrightarrow{OC})\;;\ (\overrightarrow{OB}\;,\ \overrightarrow{OC})$

Exercice 13

$ABC$ est un triangle équilatéral direct. On construit à l'extérieur le carré $ABED.$ Quelles sont les mesures principales en radians des angles orientés suivants :

$(\overrightarrow{AB}\;,\ \overrightarrow{AC})\;;\ (\overrightarrow{AB}\;,\ \overrightarrow{AD})\;;\ (\overrightarrow{BC}\;,\ \overrightarrow{BE})$

$(\overrightarrow{CB}\;,\ \overrightarrow{CE})\;;\ (\overrightarrow{EC}\;,\ \overrightarrow{EB})\;;\ (\overrightarrow{BC}\;,\ \overrightarrow{BD})$

$(\overrightarrow{CB}\;,\ \overrightarrow{CD})\;;\ (\overrightarrow{EC}\;,\ \overrightarrow{EA})\ ?$

Exercice 14

On considère un losange $ABCD$ dont les diagonales se coupent en $O$ et tel que : $$(\overrightarrow{BA}\;,\ \overrightarrow{BD})=-54^{\circ}.$$

Quelles sont les mesures principales en radians des angles orientés suivants :

$(\overrightarrow{BA}\;,\ \overrightarrow{BD})\;;\ (\overrightarrow{BC}\;,\ \overrightarrow{BD})\;;\ (\overrightarrow{BD}\;,\ \overrightarrow{BC})$

$(\overrightarrow{BA}\;,\ \overrightarrow{BC})\;;\ (\overrightarrow{DA}\;,\ \overrightarrow{DC})\;;\ (\overrightarrow{OC}\;,\ \overrightarrow{OB})$

$(\overrightarrow{OA}\;,\ \overrightarrow{OC})\ ?$

Exercice 15

$ABC$ est un triangle rectangle isocèle de sens indirect. On construit le triangle équilatéral $BCE$ de manière que $E$ appartienne au demi-plan de frontière $(BC)$ contenant $A.$

Quelles sont les mesures principales en radians des angles orientés suivants :

$(\overrightarrow{AB}\;,\ \overrightarrow{AC})\;;\ (\overrightarrow{CB}\;,\ \overrightarrow{CE})\;;\ (\overrightarrow{CA}\;,\ \overrightarrow{CB})$

$(\overrightarrow{BA}\;,\ \overrightarrow{BC})\;;\ (\overrightarrow{EA}\;,\ \overrightarrow{EC})\;;\ (\overrightarrow{CA}\;,\ \overrightarrow{CE})$

$(\overrightarrow{EA}\;,\ \overrightarrow{EB})\;;\ (\overrightarrow{AE}\;,\ \overrightarrow{AB})\ ?$

Exercice 16

On donne dans le plan orienté $P$, une demi-droite $Ox.$

1) Construire les demi-droites $Oy\;,\ Oz\;,\ Ot$ telles que :

$(Ox\;,\ Oy)=\dfrac{2\pi}{3}\;,$
$\quad$
$(Ox\;,\ Oz)=-\dfrac{5\pi}{6}\;,$
$\quad$
$Ox\;,\ Ot)=\dfrac{\pi}{4}$

2) Calculer la mesure principale en radians des angles orientés

$(Oy\;,\ Oz)\;,\ (Oz\;,\ Ot)\;,\ (Ot\;,\ Oy).$

Exercice 17

On considère un carré $ABCD$ tel que $(\overrightarrow{AB}\;,\ \overrightarrow{AD})=\dfrac{\pi}{2}.$

1) Construire les demi-droites $Ax\;,\ Cy$ et $Cz$ telles que :

$(\overrightarrow{AB}\;,\ Ax)=\dfrac{\pi}{6}\;,$
$\quad$
$(\overrightarrow{CB}\;,\ Cy)=\dfrac{\pi}{6}\;,$
$\quad$
$(\overrightarrow{CB}\;,\ Cz)=-\dfrac{\pi}{6}$

2) $Ax$ et $Cy$ se coupent en $E.$ Démontrer que $(Ax)$ et $(Cy)$ sont orthogonales.

En déduire que le quadrilatère $ABCE$ est inscriptible dans un cercle dont on précisera le centre et le rayon.

3) $Ax$ et $Cz$ se coupent en $R.$ Démontrer que $R$ est équidistant des points $A$ et $C.$ En déduire que les points $B\;,\ R\;,\ D$ sont alignés.

Exercice 18

On considère un rectangle $ABCD$ tel que $(\overrightarrow{AB}\;,\ \overrightarrow{AD})=\dfrac{\pi}{2}.$ On note $\alpha$ la mesure principale de l'angle orienté $(\overrightarrow{AB}\;,\ \overrightarrow{AC}).$

1) Construire les demi-droites $Dx\text{ et }Dy$ telles que : $$(\overrightarrow{DA}\;,\ Dx)=\alpha\text{ et }(\overrightarrow{DA}\;,\ Dy)=-\alpha$$

2) Démontrer que les droites $(Dx)$ et $(AC)$ sont orthogonales, et qu'il en est de même des droites $(Dy)$ et $(DB).$

3) Les demi-droites $Dx$ et $Dy$ coupent respectivement $(AC)$ en $E$ et $F.$

Démontrer que la droite $(BD)$ est tangente au cercle passant par les points $D\;,\ E\;,\ F.$ Démontrer de même que la droite $(DF)$ est tangente au cercle circonscrit au rectangle $ABCD.$

4) Exprimer en fonction de $\alpha$ la mesure des angles non orientés $EDF\;,\ DFE$ et $DAE.$

Exercice 19

1) Soit $\cos t=\dfrac{\sqrt{2}}{4}$ et $\sin t < 0.$ Calculer $\sin t$ et $\tan t.$

2) Soit $t\in\left[\dfrac{\pi}{2}\;;\ \pi\right]$ et $\sin t=\dfrac{4}{5}.$ Calculer $\cos t$ et $\tan t$

3) Sachant que $t\in\left[\dfrac{\pi}{2}\;;\ \pi\right]$ et que $\tan t=-\sqrt{3}$ , calculer $\cos t$ et $\sin t.$

4) Sachant que $\sin\dfrac{\pi}{12}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$, calculer $\sin\left(-\dfrac{\pi}{12}\right)$ et $\sin\left(\dfrac{23\pi}{12}\right)$

5) Sachant que $\cos\dfrac{\pi}{8}=\dfrac{\sqrt{2+\sqrt{2}}}{2}$, calculer $\cos\left(-\dfrac{\pi}{8}\right)$ et $\cos\left(\dfrac{15\pi}{8}\right)$

Exercice 20 Calcul de $\cos\dfrac{\pi}{5}$ et $\cos\dfrac{2\pi}{5}$

On considère un triangle $ABC$, isocèle en $A$, tel que $BC=a$, et $\widehat{B}=\dfrac{2\pi}{5}\;\text{rad}.$ La bissectrice de l'angle $\widehat{B}$ coupe $[AC]$ en $D.$

1) Démontrer que les triangles $ABD$ et $BCD$ sont isocèles.

En déduire que : $DA=DB=a.$

2) Démontrer que : $AB=2a\cos\dfrac{\pi}{5}$ et $CD=2a\cos\dfrac{2\pi}{5}.$

En déduire que : $\cos\dfrac{\pi}{5}-\cos\dfrac{2\pi}{5}=\dfrac{1}{2}.$

3) Démontrer que : $BC=BD\cos\dfrac{\pi}{5}+CD\cos\dfrac{2\pi}{5}.$

En déduire que : $\cos\dfrac{\pi}{5}\cos\dfrac{2\pi}{5}=\dfrac{1}{4}.$

4) On pose : $x=\cos\dfrac{\pi}{5}$ et $y=\cos\dfrac{2\pi}{5}.$ On sait que $x-y=\dfrac{1}{2}$ et $xy=\dfrac{1}{4}.$

En utilisant $(x+y)^{2}=(x-y)^{2}+4xy$, calculer $x+y$, et en déduire $x$ et $y.$

(On trouvera que : $\cos\dfrac{\pi}{5}=\dfrac{\sqrt{5}+1}{4}$ et $\cos\dfrac{2\pi}{5}=\dfrac{\sqrt{5}-1}{4}).$

Exercice 21

Démontrer que, pour tout réel $t$ :

1) $(\cos t+\sin t)^{2}=1+2\cos t\sin t$

2) $(\cos t-\sin t)^{2}=1-2\cos t\sin t$

$3)\ (\cos t+\sin t)^{2}+(\cos t-\sin t)^{2}=2$

$4)\ (\cos t+\sin t)^{2}-(\cos t-\sin t)^{2}=4\sin t\cos t$

5) $\sin^{4}t-\cos^{4}t=\sin^{2}t-\cos^{2}t$

6) $\sin^{4}t-\cos^{4}t+2\cos^{2}t=1$

Exercice 22

Exprimer en fonction de $\sin t$ et $\cos t$ les expressions suivantes :

$A=\cos(t+\pi)+\cos(t+2\pi)+\cos(t-\pi)+\cos(t-3\pi)$

$B=\sin(t+\pi)+\sin(t+2\pi)+\sin(t-\pi)+\sin(t-3\pi)$

$C=\sin\left(t+\dfrac{\pi}{2}\right)+\cos(t-\pi)+\sin\left(t+\dfrac{3\pi}{2}\right)+\cos(t+\pi)$

$D=\sin\left(\dfrac{3\pi}{2}+t\right)+\cos\left(\dfrac{27\pi}{2}-t\right)+\sin(3\pi+t)-\cos(7\pi-t)$

Exercice 23

Soit $ABC$ un triangle isocèle à angles aigus $(AB=AC=a\;;\ \widehat{A}=2\alpha).$

1) Calculer $BC.$

2) Calculer la hauteur $BH$ de deux façons différentes et en déduire la relation : $$\sin 2\alpha=2\sin\alpha\cos\alpha$$

3) Calculer $AH$ et $CH$ et en déduire la relation : $$cos 2\alpha=1-2\sin^{2}\alpha$$

Exercice 24

Exprimer à l'aide de $\tan t$ les expressions :

$X=\dfrac{\sin^{3}t-\cos^{3}t}{\sin t-\cos t}\ ;$
$\quad$
$Y=\cos^{2}t-\sin t\cos t\ ;$
$\quad$
$Z=\dfrac{\sin^{2}t+\sin t\cos t}{\sin^{2}t-\cos^{2}t}$