Série d'exercices : Projection orthogonale dans le plan 4e
Classe:
Quatrième
Exercice 1 Projection orthogonale
Soit $ABC$ un triangle rectangle en $A.$
1) a) Quel est le projeté orthogonal de $B$ sur $(BC)$ ?
b) Quel est le projeté orthogonal de $C$ sur la $(AB)$ ?
2) a) Marquer le point $H$, projeté orthogonal de $A$ sur $(BC).$
b) Que représente $[AH]$ pour le triangle $ABC$ ?
3) a) Quel est le projeté orthogonal de $[AC]$ sur $(BC)$ ?
b) Quel est le projeté orthogonal de $[AB]$ sur $(BC)$ ?
Exercice 2 Projection orthogonale
Tracer un triangle $ABC$ rectangle en $A.$
1) Quel est le projeté orthogonal de $B$ sur la droite $(AC)$ ? Celui de $C$ sur $(AB)$ ?
2) Marquer le point $H$, projeté orthogonal de $A$ sur $(BC).$
Que peut-on dire de $[AH]$ ?
3) Soit $I$ et $J$ les projetés orthogonaux respectifs de $H$ sur $(AB)$ et $(AC).$
Quelle est la nature du quadrilatère $AIHJ$ ?
Exercice 3 Projection orthogonale
Soit $ENS$ un triangle isocèle en $E\;;\ I$ est le milieu du segment $[EN]$ et $J$ le projeté orthogonal de $I$ sur la droite $(NS).$
Démontrer que : $BJ=\dfrac{1}{4}EN$
Exercice 4 Projection orthogonale
1) Tracer un triangle $MNP$, placer $A$ milieu de $[MN]$, puis le point $C$, pied de la hauteur issue de $N.$
2) Construire le projeté orthogonal $B$ de $A$ sur $(MP).$
3) Démontrer que $B$ est le milieu de $[MC].$
Exercice 5 Repérage
Le plan est muni d'un repère orthonormal $(O\;,\ I\;,\ J).$
1) Placer les points $A\;,\ B\;,\ C$ et $D$ tel que :
$A(-2\;;\ 1)\;;\ B(2\;;\ 3)\;;\ C(2\;;\ 0)$ et $D(-2\;;\ -2).$
2) Calculer les coordonnées de $E$ milieu $[AC]$ et $F$ celui de $[DB].$
3) Quelle est la nature du quadrilatère $ABCD$ ? Justifier.
Exercice 6 Repérage
Le plan est muni d’un repère orthonormé $(O\;;\ I\;;\ J).$
On donne $A(-2\;;\ 4)\;;\ B(-2\;;\ 4)\;;\ C(2\;;\ 0).$
1) Placer les points $A\;;\ B$ et $C.$
2) Calculer les distances : $AB^{2}\;;\ AC^{2}$ et $BC^{2}$, en déduire la nature du triangle $ABC$ ?
3) Calculer les coordonnées de $E$ centre du cercle $(\mathcal{C})$ circonscrit à $ABC.$
Exercice 7 Repérage
Le plan est muni d'un repère orthonormé $(O\;;\ I\;;\ J).$
On donne $A(0\;;\ 1)\;;\ B(3\;;\ 1)\;;\ C(1\;;\ 4)$ et $M\left(2\;;\ \dfrac{5}{2}\right).$
1) Placer les points $A\;;\ B\;;\ C$ et $M.$
2) Démontrer que $M$ est le milieu de $[BC].$
3) Calculer : $AB^{2}\;;\ AC^{2}$ et $BC^{2}$ puis montrer que $ABC$ est un triangle rectangle et isocèle en $B.$
4) Démontrer que : $BM^{2}=\dfrac{1}{4}AC^{2}.$
En déduire que : $BM=\dfrac{1}{2}AC.$
5) Calculer les coordonnées de $I$ milieu $[AC].$
6) Puis construire le cercle $(\mathcal{C})$ circonscrit à $ABC.$
Exercice 8
On considère la figure ci-dessous.
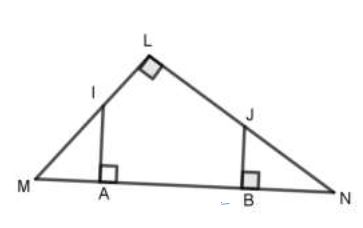
Réponds par vrai ou faux à chacune des
affirmations suivantes :
1) $I$ est le projeté orthogonal de $A$ sur $(LM).$
2) $B$ est le projeté orthogonal de $A$ sur $(BJ).$
3) $L$ est le projeté orthogonal de $M$ sur $(LN).$
4) $L$ est le projeté orthogonal de $N$ sur $(LM).$
5) $A$ est le projeté orthogonal de $N$ sur $(IA).$
Exercice 9
Dans un triangle $ABC$, on appelle $A'$ le pied de la hauteur issue de $A.$
Recopie puis complète la phrase ci-dessous.
Le point ........... est le projeté ........... du point ......... sur ...............
Exercice 10
Trace une droite $(\mathcal{D})$ et marque des points $A$, $B$ , $C$ n'appartenant pas à $(\mathcal{D})$ et un point $E$ appartenant à $(\mathcal{D}).$
Construis les points $A'$, $B'$, $C'$ et $E'$ projetés orthogonaux respectifs de $A$, $B$ , $C$ et $E$ sur $(\mathcal{D}).$
Exercice 11
Pour chacune des figures ci-dessous, une droite et un segment sont donnés.
Reproduis chaque figure et construis le projeté orthogonal du segment sur la droite.
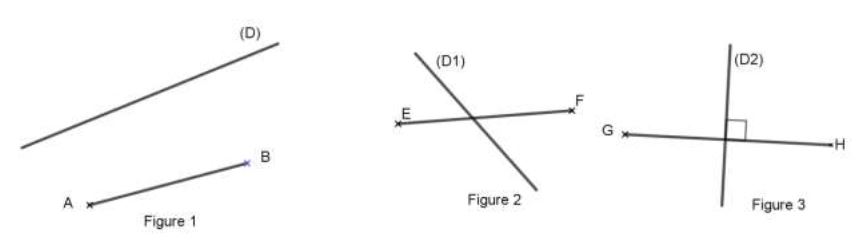
Exercice 12
Soit $ABC$ un triangle rectangle en $A.$
1) a) Quel est le projeté orthogonal de $B$ sur $(BC)$ ?
b) Quel est le projeté orthogonal de $C$ sur $(AB)$ ?
2) a) Marque le point $H$, projeté orthogonal de $A$ sur $(BC).$
b) Que représente $[AH]$ pour le triangle $ABC$ ?
3) a) Quel est le projeté orthogonal de $[AC]$ sur $(BC)$ ?
b) Quel est le projeté orthogonal de $[AB]$ sur $(BC)$ ?
Exercice 13
1) Trace un triangle $MNP$, place $A$ milieu de $[MN]$, puis le point $C$, pied de la hauteur issue de $N.$
2) Construis le projeté orthogonal $B$ de $A$ sur $(MP).$
3) Démontre que $B$ est le milieu de $[MC].$
Exercice 14
1) Trace un parallélogramme $ABCD$ de centre $O.$
2) Construis les points $E$ et $F$, projetés orthogonaux respectifs de $A$ et $C$ sur $(BD).$
$G$ et $H$, projetés orthogonaux respectifs de $B$ et $D$ sur $(AC).$
Quelle est la nature du quadrilatère $EGFH$ ? Justifie.
Exercice 15
Soit $ENS$ un triangle isocèle en $E$ ; $I$ est le milieu du segment $[EN]$, $K$ milieu de $[NS]$ et $J$ le projeté orthogonal de $I$ sur la droite $(NS).$
Démontre que :
$NJ=\dfrac{1}{4}NS.$
Exercice 16
Le plan est muni d'un repère orthonormal $(O\;,\ I,\ J).$
1) Place les points $A(-2\;;\ 1)\;;\ B(2\;;\ 3)\;;\ C(2\;;\ 0)\text{ et }D(-2\;;\ -2).$
2) Calcule les coordonnées de $E$ milieu $[AC]$ et $F$ milieu de $[DB].$
3) Quelle est la nature du quadrilatère $ABCD$ ? Justifie.
Exercice 17
Le plan est muni d'un repère orthonormal $(O\;;\ I\;;\ J).$
On donne $A(-2\;;\ 4)\;;\ B(-2\;;\ -4)\;;\ C(2\;;\ 0).$
1) Place les points $A$ ; $B$ et $C.$
2) Calcule les distances :
$AB^{2}$ ; $AC^{2}$ et $BC^{2}$, en déduis la nature du triangle $ABC$ ?
3) Calcule les coordonnées de $E$ centre du cercle $(\mathcal{C})$ circonscrit à $ABC.$
Exercice 18
Le plan est muni d'un repère orthonormé $(O\;;\ I\;;\ J).$
On donne
1) Place les points $A(0\;;\ -1)\;;\ B(3\;;\ 1)\;;\ C(1\;;\ 4)\text{ et }M\left(2\;;\ \dfrac{5}{2}\right).$
2) Démontre que $M$ est le milieu de $[BC].$
3) Montre que $ABC$ est un triangle rectangle et isocèle en $B.$
4) Démontre que :
$BM^{2}=\dfrac{1}{4}A^{2}B^{2}.$
5) Détermine les coordonnées du point $I$ centre du cercle circonscrit au triangle $ABC.$
Exercice 19
Le plan est muni d'un repère orthonormal $(O\;,\ I\;,\ J).$
On donne les points $V(-3\;;\ 3)\;,\ A(3\;;\ 5)\text{ et }S(5\;;\ -1)$
1) Détermine la nature du triangle $VAS.$
2) Soit $B$ le milieu de $[VS]$ et $E$ le symétrique de $A$ par rapport à $B.$
a) Calcule les coordonnées de $B$ et $E.$
b) Démontre que le quadrilatère $VASE$ est un carré.

Commentaires
Anonyme (non vérifié)
mer, 04/26/2023 - 22:33
Permalien
comment justifier qu'un
Anonyme (non vérifié)
mer, 04/26/2023 - 22:35
Permalien
merci pour les exercices
Ndiaye (non vérifié)
sam, 05/18/2024 - 00:27
Permalien
Math
Ajouter un commentaire