Série d'exercices sur les angles orientés et trigonométrie 1e S
Exercice 1
1) $(1+\sin x+\cos x)^{2}=(1+\sin x)(1+\cos x)$
2) $\cot^{2}x-\cos^{2}x=\cot^{2}x\cos^{2}x$
3) $\dfrac{1-\sin x}{\cos x}=\dfrac{\cos x}{1+\sin x}$
4) $\tan^{2}x+\cot^{2}x=\dfrac{1}{\sin^{2}x\cos^{2}x}-2$
5) $2(\sin^{6}x+\cos^{6}x)-3(\sin^{4}+\cos^{4}x)+1=0$
6) $\sin^{2}x-\sin^{2}y=\dfrac{1}{1+\tan^{2}y}-\dfrac{1}{1+\tan^{2}x}$
Exercice 2
$a)\ \alpha-5\pi\;;\qquad b)\ -\alpha-\pi\;;\qquad c)\ -\alpha-2\pi$
$d)\ -\alpha-\dfrac{\pi}{2}\;;\qquad e)\ \alpha-\dfrac{9\pi}{2}\;;\qquad f)\ -\alpha+\dfrac{5\pi}{2}$
Exercice 3
$a)\ 3\pi\;,\ -5\pi\;,\ \dfrac{3\pi}{2}\;;\qquad b)\ \dfrac{3\pi}{4}\;,\ -\dfrac{7\pi}{4}\;,\ \dfrac{15\pi}{4}$
$c)\ -\dfrac{2\pi}{3}\;,\ \dfrac{5\pi}{3}\;,\ \dfrac{8\pi}{3}\;;\qquad d)\ \dfrac{7\pi}{6}\;,\ \dfrac{13\pi}{6}\;,\ \dfrac{31\pi}{6}$
Exercice 4
$A=\sin\left(\dfrac{\pi}{2}-\alpha\right)-\cos(-\alpha+2k\pi)+\cos(3\pi+\alpha)+\sin\left(\alpha-\dfrac{7\pi}{2}\right)$
$B=2\tan\left(\alpha+\dfrac{3\pi}{2}\right)+\tan\left(\alpha-\dfrac{5\pi}{2}\right)+3\cot(\alpha+k\pi)-\cot[(2h+1)\pi-\alpha]$
$C=\dfrac{\cos\left(3\alpha+\dfrac{3\pi}{2}\right)+\cos\left(\dfrac{5\pi}{2}-3\alpha\right)+\sin(3\alpha+k\pi)}{\cos(3\alpha-\pi)+\cos(k\pi+3\alpha)+3\sin\left(\dfrac{3\pi}{2}-3\alpha\right)}$
Exercice 5
On demande $\cos \alpha$ et $\tan \alpha$
$1)\ \alpha\in\;\left[-\dfrac{\pi}{2}\;;\ 0\right]\text{ et }\sin \alpha=-0.6$
$2)\ \alpha\in\;[0\;;\ \pi]\text{ et }\sin \alpha=\dfrac{15}{17}$
$3)\ \alpha\in\;\left[\dfrac{\pi}{2}\;;\ \pi\right]\text{ et }\sin \alpha=\sqrt{\dfrac{2}{3}}$
Exercice 6
On demande $\sin \alpha$ et $\tan \alpha$
$1)\ \alpha\in\;\left[\dfrac{-\pi}{2}\;;\ 0\right]\text{ et }\cos \alpha=\dfrac{\sqrt{5}}{3}$
$2)\ \alpha\in\;\left[\pi\;;\ \dfrac{3\pi}{2}\right]\text{ et }\cos \alpha=-0.8$
$3)\ \alpha\in\;\left[\dfrac{\pi}{2}\;;\ \pi\right]\text{ et }\cos \alpha=1-\sqrt{2}$
Exercice 7
On demande $\cos \alpha$ et $\sin \alpha$
$1)\ \alpha\in\;[0\;;\ \pi]\text{ et }\tan\alpha=-2\;;\qquad 2)\ \alpha\in\;\left[\dfrac{3\pi}{2}\;;\ 2\pi\right]\text{ et }\tan\alpha=-\dfrac{3}{4}$
$3)\ \alpha\in\;\left[\pi\;;\ \dfrac{3\pi}{2}\right]\text{ et }\tan\alpha=\dfrac{8}{15}\;;\qquad 4)\ \alpha\in\;\left[0\;;\ \dfrac{\pi}{2}\right]\text{ et }\tan\alpha=2-\sqrt{3}$
Exercice 8
$1)\ \cos\left(x-\dfrac{\pi}{2}\right)=\cos3x\;;\qquad 2)\ \cos\left(2x-\dfrac{\pi}{4}\right)=\cos\left(x+\dfrac{\pi}{6}\right)$
$3)\ \cos\left(2x+\dfrac{\pi}{3}\right)=\cos3x\;;\qquad 4)\ \cos\left(3x+\dfrac{\pi}{6}\right)=\dfrac{1}{2}$
$5)\ \cos\left(2x-\dfrac{\pi}{4}\right)=-\dfrac{1}{3}\;;\qquad 6)\ 4\cos^{2}x-3=0$
$7)\ 2\cot^{2}x=\dfrac{1}{\sin^{2}x}\;;\qquad 8)\ \sin\left(3x-\dfrac{\pi}{5}\right)=\sin\left(\dfrac{\pi}{5}-x\right)$
$9)\ \sin\left(2x+\dfrac{\pi}{3}\right)=\sin\left(\dfrac{2\pi}{3}-x\right)\;;\qquad 10)\ \sin\left(2x-\dfrac{\pi}{3}\right)=\sin\left(x+\dfrac{\pi}{4}\right)$
$11)\ \sin\left(\dfrac{\pi}{3}-x\right)=\dfrac{1}{2}\;;\qquad 12)\ 4\sin^{2}x-1=0$
$13)\ \tan\left(2x-\dfrac{\pi}{3}\right)=-\sqrt{3}\;;\qquad 17)\ \sqrt{3}\tan x=3$
N.B Les équations de $n^{\circ}$ pair sont à résoudre dans $[0\;;\ 2\pi[$ et celles de $n^{\circ}$ impair dans $]-\pi\;;\ \pi]$
Exercice 9
$1)\ \sin\left(x-\dfrac{\pi}{6}\right)=\cos\left(x-\dfrac{\pi}{3}\right)\;;\qquad 2)\ \sin\left(x+\dfrac{\pi}{6}\right)=\cos\left(x+\dfrac{\pi}{3}\right)$
$3)\ \cos\left(2x+\dfrac{\pi}{3}\right)=\sin\left(5x-\dfrac{\pi}{6}\right)\;;\qquad 4)\ \tan\left(3x-\dfrac{\pi}{4}\right)=\cot 2x$
$5)\ \tan\left(x-\dfrac{\pi}{3}\right)=3\cot\left(x-\dfrac{\pi}{3}\right)\;;\qquad 6)\ \tan^{2}4x\tan^{2}x=1$
Exercice 10
$1)\ \sin2x+\cos3x=0\;;\qquad 2)\ \cos\left(\dfrac{\pi}{3}-x\right)+\sin\left(\dfrac{\pi}{4}+2x\right)=0$
$3)\ \sin^{2}\left(2x+\dfrac{\pi}{3}\right)-\sin^{2}x=0\;;\qquad 4)\ \cos^{2}4x-\sin^{2}3x=0$
$5)\ \tan2x\cot\left(\dfrac{\pi}{6}-x\right)=1\;;\qquad 6)\ 4\sin^{2}\left(x+\dfrac{\pi}{6}\right)-1=0$
Exercice 11
$1)\ \sqrt{2}\cos^{2}x-\cos x-\sqrt{2}=0\;;\qquad 2)\ 2\sin^{2}x+\sqrt{3} \sin x-3=0$
$3)\ \tan^{2}x+(\sqrt{3}-1)\tan x-\sqrt{3}=0$
$4)\ \cot^{2}x+(1-\sqrt{3})\cot x-\sqrt{3}=0$
Exercice 12
1) Discuter suivant les valeurs du paramètre $m$ le nombre de solutions de l'équation qui appartiennent à l'intervalle $[0\;;\ 2\pi[$
2) Résoudre l'équation pour $m=-\dfrac{7}{4}$
Exercice 13
2) Montrer que, lorsque l'équation admet des solutions, une de ces solutions et une seule appartient à l'intervalle $[-\dfrac{\pi}{4}\;;\ \dfrac{\pi}{4}]$.
3) Résoudre l'équation pour $m=-\dfrac{4}{\sqrt{3}}$
Exercice 14
$1)\ \sqrt{2}\cos x-1<0\;;\qquad 2)\ 2 \sin x-\sqrt{3}>0$
$3)\ 4\sin^{2}x-2(1+\sqrt{3})\sin x+\sqrt{3}<0$
$4)\ 4\sin^{2}x-2(1-\sqrt{3})\sin x-4+\sqrt{3}>0$
$5)\ \sqrt{3}\tan^{2}x-(1+\sqrt{3})\tan x+1>0$
$6)\ \tan^{2}x-3\leq 0\;;\qquad 7)\ 3\tan^{4}x-4\tan^{2}x+1<0$
$8)\ \dfrac{\tan^{2}x-2}{\tan^{2}x-1}<\dfrac{1}{2}$
$9)\ -4\cos^{2}x-2(\sqrt{2}+1)\cos x+4+\sqrt{2}\leq 0$
$10)\ \tan x-\sqrt{3}\cot x+1-\sqrt{3}>0$
$11)\ 4\sin^{2}x-2(1-\sqrt{3})\cos x-4+\sqrt{3}>0$
$12)\ \sqrt{1-4\sin^{2}x}<2\cos x-1$
$13)\ \dfrac{2}{4\cos^{2}x-1}<1\;;\qquad 14)\ \dfrac{2\cos2x-1}{1+2\cos2x}<0$
Exercice 15
$$\left\lbrace\begin{array}{lcl} \sin x+\sin y &=& 1 \\ \sin x\sin y &=& k \end{array}\right.$$
Discuter suivant les valeurs de $k$
2) Déterminer $x$ et $y$ sachant qu'ils appartiennent à $[0\;;\ 2\pi[$ et que $k=0.24$.
Formules d'addition
Exercice 16
$A(x)=1+\cos x+\cos\dfrac{x}{2}\;;\qquad B(x)=1-\cos x+\sin\dfrac{x}{2}$
Exercice 17
Exercice 18
a) $2\cos^{2}x+4\sin^{2}x$
b) $\cos^{4}x-2\sin^{2}x\cos^{2}x+\sin^{4}x$
c) $\cos^{4}x-\sin^{4}x$
Exercice 19
$\cos x=\dfrac{\sqrt{6}+\sqrt{2}}{4}\text{ et }0<x<\dfrac{\pi}{2}$
Calculer $\cos 2x$ et en déduire $x$
2) Soit le réel $x$ tel que :
$\sin x=\dfrac{\sqrt{5}-1}{2}\text{ et }0<x<\dfrac{\pi}{2}$
Calculer $\sin 2x$ et $\cos 2x$.
En déduire $x$
Exercice 20
En déduire $\cos\dfrac{3\pi}{8}\text{ et }\sin\dfrac{3\pi}{8}$
(On pourra utiliser $\cos\dfrac{\pi}{4}\text{ et }\sin\dfrac{\pi}{4})$
Exercice 21
$a)\ \cos x+\sin x=\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)\;;\qquad b)\ \cos x-\sin x=\sqrt{2}\cos\left(x+\dfrac{\pi}{4}\right)$
Exercice 23
Exercice 24
$a)\ \cos^{4}x=\dfrac{1}{8}(\cos4x+4\cos2x+3)$
$b)\ \sin^{4}x=\dfrac{1}{8}(\cos4x-4\cos2x+3)$
2) Calculer : $\cos^{4}\dfrac{\pi}{8}+\cos^{4}\dfrac{3\pi}{8}+\cos^{4}\dfrac{5\pi}{8}+\cos^{4}\dfrac{7\pi}{8}$
Exercice 25
Exercice 26
$a)\ \dfrac{7\pi}{12}=\dfrac{\pi}{3}+\dfrac{\pi}{4}\text{ et }\dfrac{\pi}{12}=\dfrac{\pi}{3}-\dfrac{\pi}{4}$
$b)\ \dfrac{5\pi}{12}=\dfrac{\pi}{4}+\dfrac{\pi}{6}\text{ et }\dfrac{\pi}{12}=\dfrac{\pi}{4}-\dfrac{\pi}{6}$
$c)\ -\dfrac{7\pi}{4}\;,\ \dfrac{5\pi}{3}\;,\ -\dfrac{23\pi}{6}\;,\ \dfrac{\pi}{8}$
Exercice 27
$1)\ \cos a\sin(b-c)+\cos b\sin(c-a)+\cos c\sin(a-b)=0$
$2)\ \sin a\sin(b-c)+\sin b\sin(c-a)+\sin c\sin(a-b)=0$
$3)\ \cos(a+b)\cos(a-b)=\cos^{2}a-\sin^{2}b=\cos^{2}b-\sin^{2}a$
Exercice 28
En déduire $\cos 3a$ en fonction de $\cos a$.
2) Calculer $\sin(a+b+c)$.
En déduire $\sin 3a$ en fonction de $\sin a$.
3) Calculer $\tan(a+b+c)$.
En déduire $\tan 3a$ en fonction de $\tan a$.
Exercice 29
$1)\ 2\cos(a+b)\sin(a-b)=\sin 2a-\sin 2b$
$2)\ 2\sin(a+b)\sin(a-b)=\cos 2b-\cos 2a$
$3)\ \tan 2a-\tan a=\dfrac{\tan a}{\cos 2a}$
$4)\ \cos^{2}2a-\sin^{2}a=\cos a \cos 3a$
Exercice 30
Par exemple, $\alpha\;,\ \beta\;,\ \gamma$ peuvent être les mesures en radians des angles non orientés d'un triangle $ABC$.
Démontrer les relations suivantes :
$1)\ \sin \alpha+\sin \beta+\sin \gamma=4\cos\dfrac{\alpha}{2}\cos\dfrac{\beta}{2}\cos\dfrac{\gamma}{2}$
$2)\ \cos \alpha+\cos \beta+\cos \gamma=1+4\sin\dfrac{\alpha}{2}\sin\dfrac{\beta}{2}\sin\dfrac{\gamma}{2}$
$3)\ \tan\alpha+\tan\beta+\tan\gamma=\tan \alpha \tan \beta \tan \gamma$
$4)\ \sin \alpha-\sin \beta+\sin \gamma=4\sin\dfrac{\alpha}{2}\cos\dfrac{\beta}{2}\sin\dfrac{\gamma}{2}$
$5)\ \sin 2\alpha+\sin 2\beta+\sin 2\gamma=4\sin \alpha\sin \beta\sin \gamma$
$6)\ \cos^{2}\alpha+\cos^{2}\beta+\cos^{2}\gamma+2\cos\alpha\cos\beta\cos\gamma=1$
$7)\ \sin^{2}\alpha+\sin^{2}\beta+\sin^{2}\gamma-2\cos\alpha\cos\beta\cos\gamma=2$
$8)\ \dfrac{\sin\alpha}{\sin\beta \sin\gamma}=\dfrac{1}{\tan \beta}+\dfrac{1}{\tan \gamma}$
$9)\ \sin \gamma=\dfrac{\sin^{2}\alpha-\sin^{2}\beta}{\sin(\alpha-\beta)}$
Exercice 31
Le point $O$, intersection des bissectrices, est le centre du cercle inscrit dans le triangle $ABC$.
$OI$ est donc un rayon de ce cercle et l'angle $OIB$ est droit.
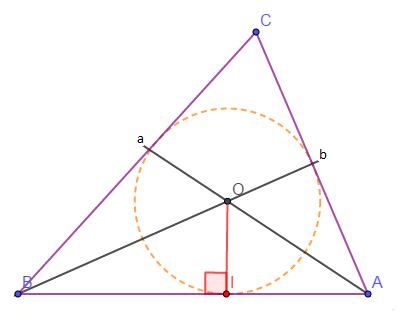
2) Calculer $\sin A\;,\ \cos A\;,\ \sin B\text{ et }\cos B$.
3) Montrer que $\sin C=\sin(A+B)$ . Calculer $\sin C$.
4) Calculer les distances $BC$ et $AC.$
Exercice 32
1) Résoudre cette équation dans $\mathbb{R}$, puis dans l'intervalle $]-\pi\;;\ \pi[$.
Représenter les solutions sur le cercle trigonométrique.
2) a) Démontrer que $\sin 3x=\sin x(4\cos^{2}x-1)$.
b) En déduire que l'équation (1) est équivalente à :
$\sin x(4\cos^{2}x+2\cos x-1)=0$.
c) Parmi les solutions trouvées pour (1) , lesquelles sont aussi solutions de l'équation :
$$(4\cos^{2}x+2\cos x-1)=0$$ ?
3) On pose $X=\cos x$.
Résoudre $4X^{2}+2X-1=0$.
En déduire les valeurs exactes de $\cos\dfrac{2\pi}{5}\text{ et }\cos\dfrac{4\pi}{5}$
Exercice 33
On considère les points $B\;,\ C\text{ et }D$ tels que :
$(\overrightarrow{OA}\;,\ \overrightarrow{OB})=x\;,\text{ avec }x\in\;\mathbb{R}\;,\ (\overrightarrow{OB}\;,\ \overrightarrow{OC})=\dfrac{2\pi}{3}\text{ et }(\overrightarrow{OC}\;,\ \overrightarrow{OD})=\dfrac{2\pi}{3}$
1) a) Faire une figure.
Donner une mesure de $(\overrightarrow{OD}\;,\ \overrightarrow{OB})$
b) Démontrer que le triangle $BCD$ est équilatéral quelle que soit la position du point $B$.
c) Montrer que $\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{O}$
d) Préciser une mesure de $(\overrightarrow{OA}\;,\ \overrightarrow{OC})\text{ et de }(\overrightarrow{OA}\;,\ \overrightarrow{OD})$ en fonction de $x.$
2) Déduire des questions précédentes que, pour tout réel $x$,
$\cos x+\cos\left(x+\dfrac{2\pi}{3}\right)+\cos\left(x+\dfrac{4\pi}{3}\right)=0$
et $\sin x+\sin\left(x+\dfrac{2\pi}{3}\right)+\sin\left(x+\dfrac{4\pi}{3}\right)=0$
3) Vérifier les deux égalités précédentes en utilisant les formules d'addition.
Exercice 34
$S_{1}=\sin\dfrac{\pi}{8}+\sin\dfrac{3\pi}{8}+\sin\dfrac{5\pi}{8}+\sin\dfrac{7\pi}{8}=0$
$S_{2}=\sin^{2}\dfrac{\pi}{8}+\sin^{2}\dfrac{3\pi}{8}+\sin^{2}\dfrac{5\pi}{8}+\sin^{2}\dfrac{7\pi}{8}=2$
$S_{3}=\sin^{4}\dfrac{\pi}{8}+\sin^{4}\dfrac{3\pi}{8}+\sin^{4}\dfrac{5\pi}{8}+\sin^{4}\dfrac{7\pi}{8}=\dfrac{3}{2}$
2) a) Vérifier que, tout réel $x\;,\ 4 \sin^{3}x=3 \sin x-\sin 3x$.
b) En déduire la valeur exacte de :
$S_{3}=\sin^{3}\dfrac{\pi}{8}+\sin^{3}\dfrac{3\pi}{8}+\sin^{3}\dfrac{5\pi}{8}-\sin^{3}\dfrac{7\pi}{8}$
Exercice 35
On considère un triangle $ABC$, isocèle en $A$, tel que $BC=a$ et $B$ mesure $\dfrac{2\pi}{5}\;\text{rad}$
La bissectrice de l'angle $B$ coupe $[AC]$ en $D$.
1) Démontrer que les triangles $ABD$ et $BCD$ sont isocèles.
En déduire que : $DA=DB=a.$
2) Démontrer que $AB=2a \cos\dfrac{2\pi}{5}$
En déduire que $\cos\dfrac{\pi}{5}-\cos\dfrac{2\pi}{5}=\dfrac{1}{2}$
3) Démontrer que $BC=BD \cos\dfrac{\pi}{5}+CD\cos\dfrac{2\pi}{5}$
En déduire que $\cos\dfrac{\pi}{5}\cos\dfrac{2\pi}{5}=\dfrac{1}{4}$
4) On pose $x= \cos\dfrac{\pi}{5}\text{ et }y=\cos\dfrac{2\pi}{5}$
On sait que $x-y=\dfrac{1}{2}\text{ et que }xy=\dfrac{1}{2}$
En utilisant $(x+y)^{2}=(x-y)^{2}+4xy$, calculer $x+y$ et en déduire $x$ et $y$.
5) Application :
Calculer les longueurs des cotés du pentagone régulier convexe et du décagone régulier convexe inscrits dans un cercle de rayon $R.$( On exprimera ces longueurs en fonction de $R$)
Exercice 36
La droite passant par $O$ et orthogonale à $(AB)$ coupe $\mathcal{C}$ en $O.$
Soit $M$ un point de l'arc $BC$ distinct de $B$ et $C.$
On note $x$ la mesure en radians de l'angle $MAB.$
1) Démontrer que $MOB=2x$.
2) La tangente en $M$ à $\mathcal{C}$ coupe la droite $(AB)$ en $D.$
a) Exprimer $MA$ et $MD$ en fonction de $R$ et $x.$
b) Déterminer $x$ de manière que $MA=MD$.
c) Déterminer $x$ de manière que $MA=2MD.$
Exercice 37
Exprimer $C$ en fonction de $B$ et démontrer que : $0<C<\dfrac{\pi}{2}$
2) Calculer en fonction de $C$ et de la longueur $a=BC$ :
a) le rayon $R$ du cercle circonscrit au triangle $ABC$.
b) les longueurs $b=AC\text{ et }c=AB.$
c) l'aire du triangle $ABC.$
Exercice 38
$a=b \cos C+c \cos B\;;\qquad b=c \cos A+a \cos C\;;\qquad c=a \cos B+b \cos A.$
Exercice 39
Soient $O$ le centre du cercle circonscrit et $H$ l'orthocentre.
1) Démontrer que : $AH=2R \cos A$ et que l'angle $OAH$ est égal à $|B-C|$.
2) Calculer $OH^{2}$ en fonction de $R\;,\ A\text{ et }(B-C)$.
3) En déduire que : $OH^{2}=9R^{2}-(a^{2}+b^{2}+c^{2})$.
Exercice 40
Relations métrique dans un triangle
On a alors les trois relations fondamentales suivantes :
Formule d'Al-Kashi : $a^{2}=b^{2}+c^{2}-2bc\cos A$
Formule de l'aire du triangle : $S=\dfrac{1}{2}bc\sin A$
Formule des sinus : $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$
$p$ désigne le demi périmètre du triangle $ABC$
$\left(p=\dfrac{1}{2}(a+b+c)\right)$
On note $R$ le rayon du cercle circonscrit à $ABC\;,\ r$ le rayon du cercle inscrit.
On note enfin $h_{A}\;,\ h_{B}\text{ et }h_{C}$ les longueurs des hauteurs $[AA']\;,\ [BB']\text{ et }[CC']$.
1) Montrer l'égalité :
$\sin A=\dfrac{2}{bc}\sqrt{p(p-a)(p-b)(p-c)}$
(on pourra utiliser l'expression de $\cos A$ tirée de la formule d'Al-Kashi et la relation : $\cos^{2}A+sin^{2}A=1$).
2) Montrer l'égalité :
$S=\sqrt{p(p-a)(p-b)(p-c)}$
(on pourra utiliser la formule de l'aire d'un triangle).
3) Donner une expression de $h_{A}$ à l'aide des nombres réels $a\;,\ b\text{ et }c$ uniquement (utiliser 2) ).
4) On introduit le point $B_{1}$ diamétralement opposé à $B$ sur le cercle circonscrit.
Utiliser une relation entre les angles $BAC$ et $B_{1}BC$ pour en déduire l'égalité :
$S=2R \sin A$
Établir les égalités :
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
5) Montrer l'égalité :
$h_{A}=\dfrac{2S}{a}$
6) Montrer l'égalité :
$S=pr.$
On pourra diviser le triangle $ABC$ en six triangles à l'aide du point $\omega$, centre du cercle inscrit.
Les résultats précédents permettent de calculer $S\;,\ h_{A}\;,\ r\text{ et }R$ à l'aide de $a\;,\ b\text{ et }c$
uniquement. On pourra les utiliser dans les exercices qui suivent.
Exercice 41
Calculer son aire, les longueurs de ses hauteurs, le rayon des cercles inscrit et circonscrit à ce triangle, les hauteurs de ses médianes.
Exercice 42
1) On donne :
$a+b=480\;;\quad \hat{A}=70^{\circ}\;,\ \hat{B}=50^{\circ}$
2) On donne :
$S=25\;;\ ab=78\;;\ \hat{B}+\hat{C}=70^{\circ}$
3) On donne :
$h_{A}=8\;;\ h_{B}=12\;;\ h_{C}=18$
Exercice 43
1) $\dfrac{1}{h_{A}}+\dfrac{1}{h_{B}}+\dfrac{1}{h_{C}}=\dfrac{1}{r}$
2) $\dfrac{abc}{a+b+c}=2rR$
3) $a^{2}+b^{2}>\dfrac{c^{2}}{2}$
4 $bc=2Rh_{A}$
Exercice 44
Démontrer que le cercle de diamètre $[BC]$ est tangent en $A$ à $(OO')$.
Calculer $BC$ en fonction de $R$ et $R'$.
Exercice 45
Soit $\alpha$ un réel fixé.
Soit $AOB$ un triangle rectangle en $O$, tel que $OA=3a\text{ et }OB=4a$
1) a) Déterminer $\Gamma_{\alpha}$, ensemble des points $M$ du plan tels que :
$\alpha MO^{2}+MA^{2}+MB^{2}=25a^{2}$.
b) Lorsque $\Gamma_{\alpha}$ est un cercle de centre $\Omega_{\alpha}$,
déterminer l'ensemble des points $\Omega_{\alpha}$ quand $\alpha$ décrit $\mathbb{R}$.
c) Le point $O$ est sur $\Gamma_{\alpha}$.
Démontrer que $\Delta$, tangente en $O$ à $\Gamma_{\alpha}$ est une droite indépendante de $\alpha$.
Caractériser $\Delta$
d) Soit $N$ un point quelconque de $\Delta$.
Démontrer que $N$ a même puissance pour tous les cercles $\Gamma_{\alpha}$
e) Soit $E$ un point fixé de $\Delta$.
On mène par $E$ deux tangentes à un cercle $\Gamma_{\alpha}$.
L'une d'elles est $(EO)$; l'autre est tangente à $\Gamma_{\alpha}$ en $T_{\alpha}$.
Déterminer l'ensemble des points $\Omega_{\alpha}$ quand $\alpha$ décrit $\mathbb{R}$.
2) Déterminer l'ensemble des points $M$ du plan tels que :
$4MA=3MB$.
Déterminer les points $M$ du plan vérifiant à la fois :
$MO^{2}+MA^{2}+MB^{2}=25a^{2}\text{ et }4MA=3MB.$

Commentaires
Diaw (non vérifié)
jeu, 05/16/2019 - 13:32
Permalien
C intéressant
Anonyme (non vérifié)
mar, 11/02/2021 - 11:41
Permalien
Très intéressant
Menan kouame gustave (non vérifié)
jeu, 06/23/2022 - 09:48
Permalien
demande de correction
Xavier (non vérifié)
lun, 04/15/2024 - 20:02
Permalien
Correction
Awity ange (non vérifié)
ven, 10/20/2023 - 07:49
Permalien
Demande d'informations
Xavier (non vérifié)
lun, 04/15/2024 - 20:03
Permalien
Mathe correction
Xavier (non vérifié)
lun, 04/15/2024 - 20:04
Permalien
Les corrections
Babakan (non vérifié)
dim, 05/19/2024 - 17:56
Permalien
Ajout dans la correction des exercices de math et de pc
Ajouter un commentaire