Série d'exercices : Symétrie orthogonale - 6e
Classe:
Sixième
Exercice 1
1) Reproduire la figure ci-dessous.
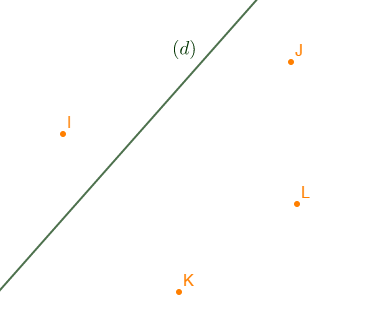
2) Construire les points $I'\;,\ J'\;,\ K'$ et $L'$ symétriques respectifs des points $I\;,\ J\;,\ K$ et $L$ par rapport à $(d).$
Exercice 2
1) Construire une droite $(d)$ médiatrice du segment $[AB]$ tel que $AB=5.5\;cm.$
2) Quel est le symétrique de $[AB]$ par rapport à $(d)\; ?$
Exercice 3
1) Construire un segment $[AB]$ oblique tel que : $AB=5\;cm$ et une droite $(d)$ extérieur de $[AB].$
2) Construire les points $A'$ et $B'$ symétrique respectifs de $A$ et $B$ par rapport à $(d).$
3) Donner la longueur de $[A'B'].$ Justifier.
Exercice 4
1) Construire un segment $[MN]$ oblique tel que : $MN=5\;cm$ ; $I$ milieu de $[MN].$
2) Construire une droite $(d)$ extérieur de $[MN].$
3) Construire les points $M'$ et $N'$ symétriques respectifs de $M$ et $N$ par rapport à $(d).$
4) a) Quel est le symétrique de $I$ par rapport à $(d)$ ? Justifier la réponse.
b) Quelle est la longueur du segment $[M'N']$ ? Justifier la réponse.
Exercice 5
1) Construire un cercle $(\mathcal{C})$ de centre $O$ est de rayon $3\;cm.$
2) Tracer une droite $(d)$ extérieur de $(\mathcal{C}).$
3) Construire le cercle $(\mathcal{C}')$ symétrique de $(\mathcal{C})$ par rapport à $(d).$
4) a) Quel est la position relative de $(\mathcal{C})$ et $(\mathcal{C}')$ ?
b) Calculer l'aire du cercle $(\mathcal{C}').$
Exercice 6
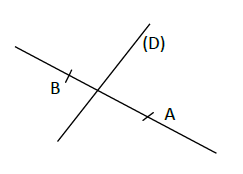
1) Construire deux droites $(D)$ et $(L)$ sécantes en $A$ tels que $(D)$ et $(L)$ ne soient pas perpendiculaires.
2) Construire la droite $(L')$ symétrique de $(L)$ par rapport à $(D).$
Exercice 7
1) Construire deux droites parallèles $(D)$ et $(L)$
2) Construire la droite $(L')$ symétrique de $(L)$ par rapport à $(D).$
Exercice 8
1) Construire un angle $AOB$ tel que $mes\;\widehat{AOB}=60^{\circ}.$
2) Construire l'angle $\widehat{B'OB}$ symétrique de l'angle $\widehat{AOB}$ par rapport à la droite $(OB).$
3) Quelle est la mesure de l'angle $\widehat{AOB'}$ ? Justifier la réponse.
Exercice 9
1) Citer huit lettres alphabets français admettant des axes de symétries.
2) Citer une lettre alphabet français admettant plusieurs axes de symétrie.
Exercice 10
Donner deux chiffres admettant un seul axe de symétrie.
Exercice 11
Citer trois figures géométriques admettant un ou des axes de symétries.
Exercice 12
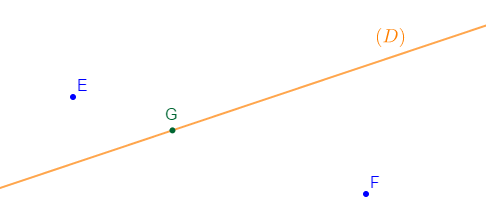
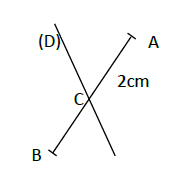
1) Reproduis la figure ci-dessous.

2) Construis à l'aide de la règle et de l'équerre le point $E'$ symétrique du point $E$ par rapport à la droite $(D).$
3) Construis à l'aide du compas le point $F'$ symétrique de $F$ par rapport à la droite $(D).$
4) Construis le symétrique du point $G$ par rapport à la droite $(D).$
Exercice 13
Recopie et complète les phrases ci-dessous :
1) Si $A'$ est le symétrique de $A$ par rapport à une droite $(D)$ alors $(D)$ est la $\ldots\ldots$ du segment $[AA'].$
2) L'axe de symétrie d'une figure est la droite $(D)$ telle que le $\ldots\ldots$ de tout point de la $\ldots\ldots$ est un point de la figure.
3) Deux segments $\ldots\ldots$ par rapport à une droite ont la même $\ldots\ldots$
Exercice 14
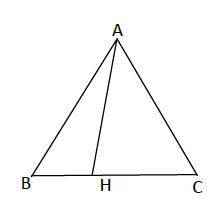
Reproduis la figure ci-dessous où $ABC$ est un triangle tel que $AH=4\;cm\;,\ BH=2\;cm\ $ et $\ HC=3\;cm.$

1) Construis le symétrique $K$ du point $H$ par rapport à la droite $(AB).$
2) Construis le symétrique $L$ du point $H$ par rapport à la droite $(AC).$
3) Les points $K\ $ et $\ L$ sont-ils symétriques par rapport à $(AH)\ ?$
Exercice 15
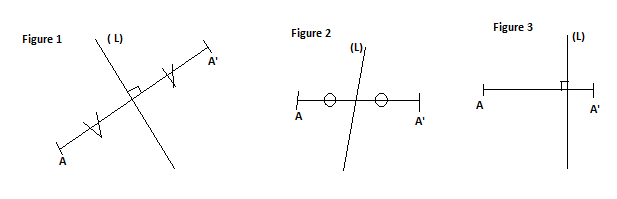
Parmi les figures ci-dessous, indique celle pour laquelle $A\ $ et $\ A'$ sont symétriques par rapport à la droite $(L).$ Justifie ta réponse.

Exercice 16
Reproduis la figure ci-dessous et trace la droite $(D')$ symétrique de la droite $(D)$ par rapport à la droite $(AB).$

Exercice 17
Sur la figure ci-dessous, le segment $[AB]$ de longueur $8\;cm$ coupe la droite $(D)$ en $C$ avec $AC=2\;cm.$

1) Construis le symétrique $A'\ $ de $\ A$ par rapport à la droite $(D).$
2) Construis le symétrique $B'\ $ de $\ B$ par rapport à la droite $(D).$
3) Quel est le symétrique de $C$ par rapport à la droite $(D)\ ?$
Les points $A'\;,\ C\ $ et $\ B'$ sont-ils alignés ?
4) Donne la longueur des segments $[CA']\ $ et $\ [CB'].$
5) Énonce la règle du cours qui permet d'affirmer ces résultats.
Exercice 18
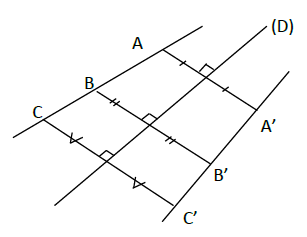
On donne la figure ci-dessous :

1) Les droites $(AB)\ $ et $\ (B'C')$ sont-elles symétriques par rapport à $(D)\ ?$
2) Les segments $[AB]\ $ et $\ [B'C']$ sont-ils symétriques par rapport à $(D)\ ?$
3) Les segments $[AB]\ $ et $\ [B'A']$ sont-ils symétriques par rapport à $(D)\ ?$
4) Les demi-droites $[AB)\ $ et $\ [B'A')$ sont-elles symétriques par rapport à $(D)\ ?$
5) Les demi-droites $[AB)\ $ et $\ [A'C')$ sont-elles symétriques par rapport à $(D)\ ?$
Exercice 19
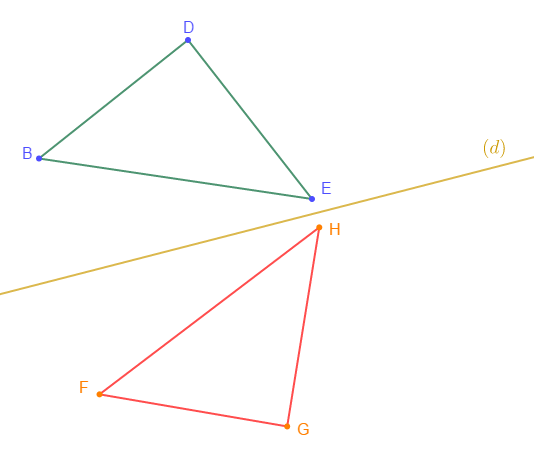
Sur la figure ci-dessous, les deux triangles sont symétriques par rapport $(d).$

Recopie et complète les phrases ci-dessous :
1) Le symétrique du point $D$ par rapport $(d)$ est le point $\ldots\ldots$ ;
2) Le symétrique du point $F$ par rapport $(d)$ est le point $\ldots\ldots$ ;
3) Le symétrique du segment $[HF]$ par rapport $(d)$ est le segment $\ldots\ldots$ ;
4) Le symétrique du segment $[ED]$ par rapport $(d)$ est le segment $\ldots\ldots$ ;
Exercice 20
1) Trace $[AB]$ de longueur $8\;cm$ puis la droite $(d)$ sécante à $(AB)$ en $C$ telle que $AC=2\;cm.$
2) Construis le symétrique $A'$ de $A$ par rapport à la droite $(d).$
3) Construis le symétrique $B'\ $ de $\ B$ par rapport à la droite $(d).$
4) Justifie que les points $A'\;,\ C\ $ et $\ B'$ sont alignés.
5) Quelle est la longueur de $[CA']\ $ et $\ [CB']\ ?$
Exercice 21
1) Construis un triangle $ABC$ isocèle en $A$ tel que $AB=6\;cm\ $ et $\ BC=4\;cm.$
2) Construis l'axe de symétrie $(D)$ de ce triangle.
3) Construis le point $E$ symétrique de $A$ par rapport à $(BC).$ Justifie que $E\in(D).$
4) Que représente $(D)$ pour le quadrilatère $ABEC\ ?$
5) Que représente $(BC)$ pour le quadrilatère $ABEC\ ?$
6) Quelle est la nature du quadrilatère $ABEC\ ?$
Exercice 22
Soient $B\ $ et $\ E$ des points d'une demi-droite $[Ax)$ tel que $AB=2.5\;cm\ $ et $\ AE=5\;cm.$
1) Construis la droite $(D)$ perpendiculaire à $(AE)$ et passant par le point $B.$
2) Que représente la droite $(D)$ pour le segment $[AE].$
3) Place un point $M$ de la droite $(D)$ situé à $4.5\;cm$ de $B.$
4) Quelle est la nature du triangle $AME\ ?$ Justifie ta réponse.
Exercice 23
1) Trace une droite $(\Delta)$ puis place trois points $R\;,\ N\ $ et $\ M$ tels que $M$ appartient à $(\Delta)$ et les points $R\ $ et $\ N$ ne se situent pas du même côté par rapport à $(\Delta).$
2) Construis les droites $(D_{1})\ $ et $\ (D_{2})$ perpendiculaires à $(\Delta)$ et passant respectivement par les points $M\ $ et $\ N.$
3) Construis la droite $(D_{3})$ passant par le point $R$ et qui est parallèle à $(\Delta).$
4) Donne la position relative des droites $(D_{2})\ $ et $\ (D_{1}).$
5) Donne la position relative de $(D_{3})\ $ et $(D_{1})$, puis celle de $(D_{3})\ $ et $\ (D_{2})$ ; justifie tes réponses.
6) Quelle serait la position relative de $(D_{1})\ $ et $(D_{2})$ si le point $N$ appartenait à $(D_{1})\ ?$
Exercice 24
Trace un segment $[RA]$ de longueur $5.80\;cm$
Soit $K$ un point du plan tel que $AK=KR.$
1) Où se situe le point $K\ ?$ Justifie ta réponse.
2) Place le point $H$ symétrique de $K$ par rapport à la droite $(RA).$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Ndong (non vérifié)
dim, 01/24/2021 - 14:56
Permalien
Enregistrer
Ndong (non vérifié)
dim, 01/24/2021 - 14:56
Permalien
Enregistrer
Saliou Ndiaye (non vérifié)
ven, 04/23/2021 - 01:05
Permalien
Math mon préféré
Ajouter un commentaire