Série d'exercices : Systèmes d'équations et d'inéquations à deux inconnues - 2nd
Classe:
Seconde
Exercice 1
En utilisant la méthode de Cramer, résoudre dans $\mathbb{R}\times\mathbb{R}$ les systèmes d'équations suivants :
1) $\left\lbrace\begin{array}{rcl} 4x+5y+3&=&-7 \\ 3x-2y&=&12\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} 2x+3y&=&-1\\ 5x-4y&=&9\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} 2x+3y&=&-1\\ 5x-4y&=&9\end{array}\right.$
$\quad$
3) $\left\lbrace\begin{array}{rcl} 6x-15&=&8y\\ 12y&=&5x-10\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} 9x-15y&=&-2\\ 6x-10y&=&7\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} 9x-15y&=&-2\\ 6x-10y&=&7\end{array}\right.$
5) $\left\lbrace\begin{array}{rcl} 6x+8y&=&15\\ 2x+6y&=&5\end{array}\right.$
$\quad$
6) $\left\lbrace\begin{array}{rcl} x\sqrt{2}+y\sqrt{3}&=&\sqrt{3}\\ x\sqrt{3}-y\sqrt{2}&=&\sqrt{2}\end{array}\right.$
$\quad$
6) $\left\lbrace\begin{array}{rcl} x\sqrt{2}+y\sqrt{3}&=&\sqrt{3}\\ x\sqrt{3}-y\sqrt{2}&=&\sqrt{2}\end{array}\right.$
$\quad$
7) $\left\lbrace\begin{array}{rcl}\dfrac{\sqrt{2}}{2}x+\dfrac{\sqrt{3}}{2}y&=&1\\ \\ x+y\dfrac{\sqrt{3}}{2}&=&2\end{array}\right.$
$\quad$
$8)\ \left\lbrace\begin{array}{rcl}\dfrac{x-y}{5}-3&=&\dfrac{2x}{3}+\dfrac{y}{100}\\ \\ \dfrac{4x}{8}+\dfrac{3y-2}{20}&=&-1\end{array}\right.$
$\quad$
$9)\ \left\lbrace\begin{array}{rcl} 7x-5(y+3)&=&8(x-2)+4y\\ 10(x+1)-6y&=&12(x+5)+12(y-2)\end{array}\right.$
$\quad$
10) $\left\lbrace\begin{array}{rcl}\dfrac{x}{352}+\dfrac{y}{264}&=&\dfrac{1}{132}\\ \\ \dfrac{x}{2}+\dfrac{y}{3}&=&\dfrac{1}{12}\end{array}\right.$
$\quad$
$11)\ \left\lbrace\begin{array}{rcl} (\sqrt{5}-2)x+3(3+2\sqrt{2})y&=&\sqrt{3}\\ (3-2\sqrt{2})x+(\sqrt{5}-2)y&=&1\end{array}\right.$
$\quad$
$12)\ \left\lbrace\begin{array}{rcl}\dfrac{7}{x-1}+\dfrac{3}{y-2}&=&\dfrac{4}{(x-1)(y-2)}\\ \\ \dfrac{5}{x+1}+\dfrac{2}{y}&=&\dfrac{3}{y(x+1)}\end{array}\right.$
Exercice 2
Résoudre les systèmes suivants après avoir fait un changement d'inconnues adéquat :
1) $\left\lbrace\begin{array}{rcl} \dfrac{4}{x}+\dfrac{5}{y}&=&-7\\ \dfrac{3}{x}-\dfrac{2}{y}&=&12\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} \sqrt{x}+\sqrt{y}&=&3\\ \sqrt{x}-2\sqrt{y}&=&-3\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} \sqrt{x}+\sqrt{y}&=&3\\ \sqrt{x}-2\sqrt{y}&=&-3\end{array}\right.$
$\quad$
3) $\left\lbrace\begin{array}{rcl} 4\dfrac{x-1}{x+2}+5\dfrac{y+1}{y-2}&=&-7\\ \\ 3\dfrac{x-1}{x+2}-2\dfrac{y+1}{y-2} &=&12\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} 4(x^{2}-2)+5(y^{2}-4)&=&-7\\ 3(x^{2}-2)-2(y^{2}-4)&=&12\end{array}\right.$
$\quad$
5) $\left\lbrace\begin{array}{rcl}\dfrac{4}{2x-1}+\dfrac{3}{2(3y+2)}&=&21\\ \\ \dfrac{5}{6x-3}-\dfrac{2}{15y+10}&=&19\end{array}\right.$
$\quad$
6) $\left\lbrace\begin{array}{rcl} (x-3)^{2}+y-2&=&8\\ 3(x-3)^{2}+5y-10&=&-10\end{array}\right.$
Exercice 3
a) Déterminer $a$ et $b$ pour que le système : $\left\lbrace\begin{array}{rcl} (2a-1)x+by&=&7\\ (a-2)x+(b-1)y&=&2\end{array}\right.$ admette pour solution le couple $(1\;;\ -1).$
b) Déterminer les réels $p$ et $q$ pour que l'équation du second degré $x^{2}+px+q=0$ admette pour ensemble de solutions $S=\left\{-\dfrac{1}{2}\;;\ \dfrac{1}{4}\right\}.$
Exercice 4
Résoudre dans $\mathbb{R}^{3}$ les systèmes suivants :
a) $\left\lbrace\begin{array}{rcr} 2x-3y+5z &=& 2\\ 2x+y-z &= & 1\end{array}\right.$
b) $\left\lbrace\begin{array}{rcr} 2x-y+3z &=& 13\\ 4x+y-2z &= & -1\\ 3x-2y+z &=& 10\end{array}\right.$
Exercice 5
Résoudre les systèmes suivants en discutant selon les valeurs de $m.$ (On utilisera la méthode de Cramer) :
1) $\left\lbrace\begin{array}{rcl} 2x+3y&=&5\\ 2mx-(m-1)y&=&m+1\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} x+my&=&0\\ mx+y&=&m+1\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} x+my&=&0\\ mx+y&=&m+1\end{array}\right.$
3) $\left\lbrace\begin{array}{rcl} 4x+2y&=&3\\ 2mx-3y&=&m+4\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} x+y&=&m-2\\ (m+2)x-4y&=&m^{2}-4\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} x+y&=&m-2\\ (m+2)x-4y&=&m^{2}-4\end{array}\right.$
5) $\left\lbrace\begin{array}{rcl} mx+y&=&(m+1)^{2}\\ 2x-y&=&3+2m\end{array}\right.$
$\quad$
6) $\left\lbrace\begin{array}{rcl} (m+1)x-y&=&2m+3\\ (2m+3)x-4y&=&4m+7\end{array}\right.$
$\quad$
6) $\left\lbrace\begin{array}{rcl} (m+1)x-y&=&2m+3\\ (2m+3)x-4y&=&4m+7\end{array}\right.$
Exercice 6
Résoudre les systèmes triangulaires suivants :
1) $\left\lbrace\begin{array}{rcl} 2x+3y&=&8\\ -x+3y&=&5 \\ x+8y&=&16\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} 2x+3y&=&8\\ -x+3y&=&5\\ x+8y&=&17\end{array}\right.$
$\quad$
2) $\left\lbrace\begin{array}{rcl} 2x+3y&=&8\\ -x+3y&=&5\\ x+8y&=&17\end{array}\right.$
3) $\left\lbrace\begin{array}{rcl} 3x+y&=&5\\ x-y&=&-2 \\ 2x+3y&=&7\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} 2x-y&=&-3\\ x+y&=&2\\ mx-(m-1)y&=&5\end{array}\right.$
$\quad$
4) $\left\lbrace\begin{array}{rcl} 2x-y&=&-3\\ x+y&=&2\\ mx-(m-1)y&=&5\end{array}\right.$
5) $\left\lbrace\begin{array}{rcl} -x+2y&=&-7\\ 2x-y&=&8 \\ (m+1)x+(m-1)y&=&-1\end{array}\right.$
N.B. Pour 4) et 5), on discutera suivant les valeurs de $m.$
Exercice 7
On considère les droites $D_{1}\;,\ D_{2}\;,\ D_{3}$ et $D_{4}$ d'équations respectives : $$(1)\ y=-x+2\;,\quad (2)\ x=1\;,\quad (3)\ x+y=0\;,\quad (4)\ 2x=-2y+4$$
1) Tracer ces quatre droites dans un repère orthonormal d'unité $3\;cm.$
2) En déduire, en justifiant par des arguments graphiques, le nombre de solutions des systèmes suivants :
$(E)\ \left\lbrace\begin{array}{rcl} y&=&-x+2\\ x&=&1\end{array}\right.$
$\quad$
$(E')\ \left\lbrace\begin{array}{rcl} y&=&-x+2\\ x+y&=&0\end{array}\right.$
$\quad$
$(E')\ \left\lbrace\begin{array}{rcl} y&=&-x+2\\ x+y&=&0\end{array}\right.$
$(E'')\ \left\lbrace\begin{array}{rcl} 2x&=&-2y+4\\ x&=&1\end{array}\right.$
3) Résoudre les systèmes $(E)\;,\ (E')$ et $(E'').$
Exercice 8
Résoudre graphiquement les systèmes d'inéquations suivants :
a) $\left\lbrace\begin{array}{rcr} 2|x|-y+1 &>& 0\\ x-3y-5 &\leq & 0\end{array}\right.$
b) $\left\lbrace\begin{array}{rcr} |x|+|y-1|-2 &\leq & 0\\ y-x & > & 0\end{array}\right.$
c) $\left\lbrace\begin{array}{rcr} 2x-y+1 &>& 0\\ x^{2}+y^{2}-4x+2y-4 &\geq & 0\end{array}\right.$
Exercice 9
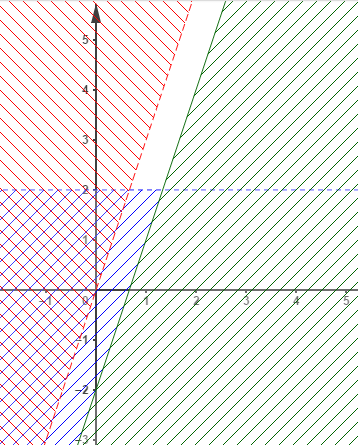
Trouver les systèmes d'inéquations associés respectivement aux graphiques ci-dessous dont les parties non hachurées constituent la solution.
a)


b)

Exercice 10
Déterminer les dimensions d'un rectangle de périmètre $126\;m$, sachant que si l'on augmente sa longueur de $7\;m$ et sa largeur de $5\;m$, son aire augmente de $400\;m^{2}.$
Exercice 11
En achetant $3$ stylos et $7$ cahiers, je paie $11600\ F$ ; en achetant $8$ stylos et $6$ cahiers (du même type), je paie $15100\ F.$ Quels sont les prix d'un stylo et d'un cahier ?
Exercice 12
On a rangé dans un hangar $159$ tabourets. Certains possèdent trois pieds, les autres $4$ pieds. Sachant que l'on dénombre $604$ pieds, déterminer le nombre de tabourets de chaque sorte.
Exercice 13 Un classique !
J'ai deux fois l'âge que vous aviez quand j'avais l'âge que vous avez. Quand vous aurez l'âge que j'ai, nous aurons, à nous deux $117$ ans.
Quel est mon âge et quel est le vôtre ?
Exercice 14
Un marchand de glaces OKIR vend des glaces en cornets, les unes à une boule, les autres à deux boules. Le but du problème est de déterminer le bénéfice maximal qu'il peut espérer faire en un jour, compte tenu de la quantité de crème glacée et du nombre de cornets dont il dispose.
On désignera par $\mathcal{P}$ un plan muni d'un repère orthonormal $(O\;;\ \vec{i}\;,\ \vec{j})$ $($unité graphique : $2.5\;mm).$
1) On note $x$ le nombre de cornets à une boule et $y$ le nombre de cornets à deux boules vendus en un jour par le marchand.
Le bénéfice réalisé est de $100\ F$ pour un cornet à une boule et $250\ F$ pour un cornet à deux boules.
Quel est le bénéfice réalisé en un jour ?
A l'aide d'inégalités faisant intervenir $x$ et $y$, exprimer chacune des conditions suivantes :
$\cdot\ $ chaque jour, le marchand dispose de $60$ cornets prévus pour une boule ;
$\cdot\ $ chaque jour, le marchand dispose de $60$ cornets prévus pour deux boules ;
$\cdot\ $ le marchand vend au plus $100$ cornets par jour ;
$\cdot\ $ le marchand dispose d'une quantité de crème glacée lui permettant de faire $150$ boules par jour.
2) Déterminer graphiquement le nombre de cornets de chaque sorte qui donnera au marchand de glaces un bénéfice maximal.
Exercice 15
Les organisateurs d'un concours proposent aux classes lauréates un voyage. Ils s'adressent à un transporteur qui dispose de $10$ cars de $40$ places et de $8$ cars de $50$ places. Les cars devront transporter $540$ personnes (les élèves et leurs accompagnateurs). Le transporteur demande $250\ 000\ F$ par autocar de $40$ places et $300\ 000\ F$ par autocar de $50$ places.
Déterminer le nombre de cars de chaque type qui occasionnera la dépense la plus faible possible pour les organisateurs.
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Commentaires
mame astou diop (non vérifié)
sam, 12/08/2018 - 14:47
Permalien
excellent
Anonyme (non vérifié)
dim, 02/23/2020 - 23:47
Permalien
Exercice 13
Anonyme (non vérifié)
ven, 03/20/2020 - 12:29
Permalien
Par enregistrement
Anonyme (non vérifié)
mer, 01/08/2025 - 00:06
Permalien
Cool
SAGNA (non vérifié)
mer, 02/09/2022 - 23:18
Permalien
demande de Correction de l'exercice 14
Ajouter un commentaire